První série dvanáctého ročníku KSP
- Termín série: 31. října 1999
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
12-1-1 Dlaždiči (10 bodů)
Firma Kostka a syn se zabývá pokládáním dlažeb všeho druhu. Momentálně má firma
bohaté zásoby velmi kvalitních dlaždiček velikosti 1×2 dm. Dlaždičky
jsou natolik kvalitní, že dokonce ani nejdou dělit (za což si prodejce samozřejmě naúčtoval
řádnou přirážku), a proto je třeba dlaždičky naskládat tak, aby nebylo potřeba je dělit.
To je ale samozřejmě pro řadového dlaždiče poněkud náročný úkol, a tak si firma najala
vás, abyste napsali program, který danou úlohu vyřeší (potřebuje totiž zjistit, jestli je
danou zakázku vůbec možno splnit). Máte tedy zadánu plochu ke dláždění
(zadanou jako matici m×n, kde 1 označuje plochu ke dláždění a 0 trávník okolo) a máte
odpovědět, zda je plochu možno vydláždit.
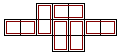 | 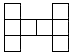 |
| Lze vydláždit | Nelze vydláždit |
12-1-2 Parník (10 bodů)
Paroplavební společnost Tit & Nick se rozhodla obohatit svůj strojový park o další parník. Chce ale, aby tento byl schopen doplout z libovolného místa do libovolného. K tomu ale potřebuje vědět, která dvě místa jsou v říční síti nejvzdálenější. A to už je úkol pro vás. Říční síť je zadána pomocí N význačných bodů na řekách a splavných úseků mezi nimi. Význačnými body jsou prameny, soutoky či ústí do moře. Splavný úsek je zadán jako dvojice význačných bodů, které spojuje. U každé dvojice je též zadáno, jak je charakterizovaný úsek řeky dlouhý. Dále víte, že říční síť tvoří strom, tedy že mezi každými dvěma význačnými body existuje právě jedna cesta. Výsledkem vašeho snažení by pak měla být dvojice nejvzdálenějších bodů v říční síti.
Příklad: Síť má 5 význačných bodů. Úseky řek jsou následující: (1, 2) o délce 3, (2, 3) o délce 4, (3, 4) o délce 2 a (2, 5) o délce 5. Nejvzdálenější body jsou 1 a 4.
12-1-3 A sort of sort (10 bodů)
Na vstupu máte N kladných celých čísel. Vaším úkolem není nic těžšího, než je co nejrychleji vzestupně uspořádat. Navíc o každém z nich víte, že je menší nebo rovno N3.
12-1-4 PRAM (10 bodů)
S rozvojem techniky se neustále rozšiřuje možnost provádět paralelní výpočty.
Z teoretického hlediska je bezpochyby rozumné zavést standardizovaný
model paralelního počítače – nejrozšířejnějším takovým modelem je PRAM,
kterému se budeme v letošním seriálu věnovat. Nutno však poznamenat,
že tento model má význam spíše v teoretické informatice – současné paralelní
počítače a výpočty na nich prováděné jsou tomuto modelu velmi vzdálené.
Parallel Random Access Machine (PRAM) je počítač tvořený k identickými
procesory. Tyto procesory sdílejí společnou (globální) paměť. Ta obsahuje
paměťové buňky číslované od nuly, jejichž počet není omezen. Do každé
buňky je možno uložit libovolné celé číslo. Na začátku výpočtu
je v několika (obvykle prvních) z nich uloženo zadání úlohy, obsah ostatních
buněk není definován. Na konci výpočtu je pak v několika (opět obvykle
prvních) buňkách uložen výsledek výpočtu. Každý z procesorů dále má
své vlastní lokální paměťové buňky pro celočíselné hodnoty, které
jsou stejně jako buňky globální paměti indexovány čísly od nuly.
Program, podle kterého probíhá výpočet, je společný pro všechny procesory a
v každém kroku provede každý procesor právě jednu instrukci. Výpočet na všech
procesorech začíná ve stejném okamžiku. Ke společné paměti přistupují
procesory přes pseudopole gmem[i], kde i je celé nezáporné číslo,
do lokální paměti přes pseudopole lmem[i] a dále si může
každý z k procesorů přečíst své číslo (od 1 do k) z pseudokonstanty
cpuid. Kromě toho může každý z procesorů použít
(nejvýše jednonásobnou) nepřímou adresaci globální paměti, tj.
lze jako index do pseudopole představujícího globální pamět použít
některý z výše uvedených výrazů. Tedy jsou správné např. výrazy typu
gmem[gmem[i]], gmem[lmem[i]], gmem[cpuid], ale nikoliv
gmem[gmem[cpuid]]. Rovněž tak nelze použít jako adresu
ve sdílené paměti jakýkoliv aritmetický výraz (kupř. mem[cpuid*3]). Nechť X, Y a Z představují
některý z výše uvedených výrazů pro přístup do paměti a k registrům,
X není cpuid, Y a Z mohou být i celočíselné
konstanty, potom instrukce PRAMu jsou tvaru:
- Přiřazení:
X:=Y - Unární minus:
X:=-Y - Součet:
X:=Y+Z - Rozdíl:
X:=Y-Z - Součin:
X:=Y*Z - Celočíselné dělení:
X:=Y/Z - Zbytek po celočíselném dělení:
X:=Y%Z - Bitová konjunkce:
X:=Y&Z - Bitová disjunkce:
X:=Y|Z - Bitová nonekvivalence:
X:=Y^Z - Bitový posun doleva:
X:=Y<<Z - Bitový posun doprava:
X:=Y>>Z - Prázdná instrukce:
nop - Ukončení výpočtu:
halt - Nepodmíněný skok:
goto LABEL - Podmíněný příkaz:
if LOGEXPR then INSTR
Bitové operace lze provádět pouze s nezápornými operandy, dělení pouze
s nenulovým dělitelem. LABEL je návěští (jako v Pascalu, pouze jej
není nutno deklarovat), definuje se napsáním LABEL: před instrukci.
Doba provádění podmíněného příkazu nezávisí na splnění jeho podmínky a
je stejná jako doba provádění libovolné jiné instrukce. INSTR je
libovolná instrukce mimo podmíněného příkazu a LOGEXPR je jeden
z následujících logických výrazů:
- Test rovnosti:
Y=Z - Negace testu rovnosti:
Y<>Z - Test ostré nerovnosti:
Y<Z, případněY>Z - Test neostré nerovnosti:
Y<=Z, případněY>=Z
Dosud jsme však opominuli jednu důležitou otázku: Co se stane,
když se více procesorů v jednom kroku pokusí zapsat několik
různých hodnot do stejné paměťové buňky? Mohou různé procesory
v jednom kroku číst ze stejné paměťové buňky? Zavedeme si několik
různých typů PRAMů podle odpovědí na tyto otázky:
- Priority Concurrent-Read Concurrent-Write (zkráceně
P-CRCW, jinak též prioritní)PRAM– hodnotu ze stejné paměťové buňky může číst a zapisovat do ní libovolný počet procesorů; do buňky bude uložena ta hodnota, kterou do ní chtěl zapsat procesor s nejnižším číslem. - Concurrent-Read Exclusive-Write (
CREW, částečně konfliktní)PRAM– hodnotu ze stejné paměťové buňky může číst libovolný počet procesorů, ale nejvýše jeden do ní může hodnotu v jednom kroku zapisovat. V případě porušení tohoto pravidla, dojde k obdobné chybě jako např. při dělení nulou. - Exclusive-Read Exclusive-Write (
EREW, bezkonfliktní)PRAM– hodnotu z libovolné paměťové buňky může číst v jednom kroku nejvýše jeden procesor a nejvýše jeden procesor se může pokusit do paměťové buňky nějakou hodnotu zapsat. V případě, že hodnota se z buňky čte a je do ní zapisována v jednom kroku, musí toto čtení a zápis provádět ten samý procesor.
Nyní si ukážeme příklady programů pro různé typy PRAMů. Jako vstup
dostanou posloupnost n čísel nula a jedna uloženou v paměťových
buňkách 1 až n; číslo n je uloženo v paměťové buňce číslo 0. Úkolem
programu je zapsat do nulté paměťové buňky pořadí první jedničky
v této posloupnosti. Pokud posloupnost obsahuje pouze nuly,
bude tato buňka obsahovat hodnotu nula. Na P-CRCW PRAMu lze úlohu vyřešit
pomocí n procesorů následujícím jednoduchým programem:
gmem[0]=0
if gmem[cpuid]=1 then gmem[0]=cpuid
halt
Tento program nelze na CREW PRAMu použít, neboť např. při druhé instrukci
zapisují všechny procesory příslušející jedničkám naráz do nulté paměťové
buňky. To obejdeme následujícím trikem (opět používáme n procesorů):
Představme si, že jsme si očíslovali prvky posloupnosti ne od jedné, ale od nuly.
V k-té etapě bude l-tý prvek (pro 2k | l) posloupnosti obsahovat
nejmenší číslo jedničky v úseku délky 2k, který jím počíná.
Nyní se procesory příslušející prvkům, jejichž číslo l je dělitelné
2k+1, a takovým, že v úseku délky 2k počínajícím l-tým prvkem
nula není, podívají na hodnotu prvku l+2k a v případě její nenulovosti ji
prohlásí za svou konečnou hodnotu. V samotném programu je ještě
třeba dbát na ošetření „plusmínusjedničkových“ chyb,
které by mohly snadno vzniknout. Program si můžete prohlédnout
na konci zadání. Jeho modifikaci pro EREW PRAM si jistě již každý dokáže vytvořit sám.
Při řešení zadaných úloh lze předpokládat, že je spuštěno (ve stejný okamžik) právě tolik procesorů, kolik požadujete. Navíc se při řešení úlohy snažte dodržovat následující pravidla (v uvedeném pořadí!):
- Počet použitých procesorů závisí na velikosti úlohy nejvýše polynomiálně.
- Celková doba výpočtu, měřená jako doba výpočtu procesoru, který skončil jako poslední, je co nejkratší.
- Velikost prostoru použitého při výpočtu, měřená jako součet počtu všech použitých buněk (v globální i lokálních pamětech), je co nejmenší.
- Počet použitých procesorů je co nejmenší (to je částečně zahrnuto v předchozí podmínce).
A nyní již lze zformulovat zadání první úlohy v tomto roce:
Vytvořte program, který jako vstup obdrží dvě nula – jedničkové posloupnosti
délky n, které představují binární čísla (nejnižší bit je poslední).
Délka posloupností je uložena v gmem[0], první posloupnost
se nachází v gmem[1] až gmem[n], druhá pak v gmem[n+1]
až gmem[2n]. V případě, že první posloupnost
představuje menší číslo než ta druhá, měla by být na konci
výpočtu v gmem[0] uložena jednička, pokud je větší, tak
dvojka, a pokud jsou si rovny, tak nula. Úlohu postupně vyřešte
na P-CRCW PRAMu, CREW PRAMu a EREW PRAMu.
Ukázkový program k úloze 12-1-4 – PRAM
lmem[0]:=gmem[0] ; tady budeme mít délku posloupnosti
lmem[1]:=cpuid ; tady budeme mít další testovanou buňku
lmem[2]:=cpuid-1 ; své číslo minus jedna
lmem[3]:=1 ; posun k další buňce
if gmem[cpuid]=1 then gmem[cpuid]:=cpuid
if gmem[cpuid]<>0 then goto 2
1: lmem[4]:=lmem[2]&lmem[3] ; Budeme končit?
if lmem[4]<>0 then goto 2 ; Končíme - dopočítali jsme.
lmem[1]:=cpuid+lmem[3]
lmem[3]:=lmem[3]<<1
if lmem[1]>lmem[0] then goto 2 ; Jsme za koncem posloupnosti.
if gmem[lmem[1]]<>0 then gmem[cpuid]:=gmem[lmem[1]]
if gmem[cpuid]=0 then goto 1 ; Ještě jsme nenašli nenulu.
2: if cpuid=1 then gmem[0]=gmem[1] ; Zapsat výsledek.
halt