Čtvrtá série třináctého ročníku KSP
- Termín série: 6. dubna 2001
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
13-4-1 Fotografové (12 bodů)
Nudlová Lhota je vesnice se skutečně příhodným jménem. Domy v ní jsou totiž postaveny pouze podle silnice, která vsí prochází, a to ještě k tomu jenom z jedné strany. Protože Nudlová Lhota je skutečně raritou, rozhodli se jí na fotografiích zachytit hned dva umělci – Alfons Různý a Adalbert Rovný. Protože omítky na domech už jsou poněkud omšelé, rozhodl se starosta, že každý dům bude pro tuto významnou událost nově natřen. Problémem ovšem je, že fotograf Alfons Různý by chtěl, aby na každé jeho fotografii byly alespoň dva domy různé barvy. Adalbert Rovný by si naopak přál, aby alespoň dva domy na každé jeho fotografii měli stejnou barvu. A aby starostí nebylo málo, tak vesničtí obyvatelé by chtěli, aby bylo použito co nejvíce barev. Protože starostovi už z toho jde hlava kolem (a ještě k tomu kouká jako sůva z nudlí), rozhodl se vás požádat o pomoc.
Vaším úkolem je navrhnout algoritmus a napsat program, který na vstupu dostane počet domů ve vsi N. Pak také dostane záběry, které by rád vyfotil Alfons Různý a záběry, které by rád vyfotil Adalbert Rovný. Každý záběr je charakterizován číslem prvního a posledního domu na záběru – domy jsou očíslovány od 1 do N. Váš program by měl pro každý dům navrhnout barvu omítky tak, aby pro každý záběr byly splněny podmínky příslušného malíře, které jsou uvedeny výše. Navíc by mělo být použito co nejvíce barev.
Příklad: Ve Lhotě je 5 domů. Alfons by rád udělal snímky 1–3, 3–5 a Adalbert snímky 1–2, 1–4.
Domy je možno obarvit třeba po řadě barvami 1, 1, 2, 3, 4 a více barev už použít nelze.
13-4-2 Okružní jízda (10 bodů)
Po zakázce pro firmu Doleva & Doprava vám byl předložen další problém z motoristického prostředí. Slavný cestovatel a závodník Mickey Louda se vsadil, že projede okružní trasu okolo své rodné země Autistánu. Protože Autistán nemá vybudovanou síť čerpacích stanic, může Mickey doplňovat benzín jen v určitých místech na trati, kde byly předtím uloženy kanystry. A protože benzín je velmi drahý, bylo na trati rozmístěno jen tolik benzínu, aby stačil právě na projetí trati. Mickey si ale uvědomil, že se mu takto může snadno stát, že skončí někde uprostřed pustiny bez jediné kapky benzínu. Proto si najal vás, abyste mu poradili, kde trasu začít, aby se mu takováto nepříjemná nehoda nestala.
Vaším úkolem je navrhnout algoritmus a napsat program, který na vstupu dostane délku okruhu v kilometrech L, počet stanovišť s benzínem K, p1… pK vzdálenosti jednotlivých stanovišť od hlavního města, které též leží na trati, a a1… aK počet kilometrů, které lze ujet s benzínem uloženým na daném stanovišti (předpokládejte, že nádrž má neomezenou kapacitu). Vaším úkolem je říci, v jaké vzdálenosti od hlavního města má Mickey započít svou okružní jízdu, aby mu nikde na trase nedošel benzím.
Příklad: Trasa je dlouhá 15 kilometrů a jsou na ní 4 stanoviště ve vzdálenostech 2, 7, 9, 13 kilometrů od hlavního města. Na stanovištích je uložen benzín na 4, 5, 3 a 3 kilometry.
Mickey může začít svůj objezd třeba na sedmém kilometru. Množství benzínu v nádrži na jednotlivých stanovištích pak bude: 0 (5), 3 (6), 2 (5), 1 (5), 0. Čísla v závorkách udávají množství benzínu po dočerpání.
13-4-3 Fazolky (9 bodů)
„Fazolky“ je hra pro jednoho hráče. Hraje se tak, že na počátku hry je N kalíšků a v těchto kalíšcích je náhodně rozmístěno N fazolí (v i-tém kalíšku je jich ai). Jediným povoleným tahem ve hře je vzít z nějakého kalíšku fazoli a přemístit ji do kalíšku sousedního. Cílem hry je, aby v každém kalíšku byla právě jedna fazole. Vaším úkolem je navrhnout algoritmus a napsat program, který pro dané N a dané počty fazolí v jednotlivých kalíšcích určí minimální počet tahů potřebný k dosažení cílového stavu.
Příklad: Počet kalíšků je 5 a počty fazolí v kalíšcích jsou 3, 0, 1, 1, 0.
K dosažení cílového stavu je třeba 5 tahů (1→2, 1→2, 2→3, 4→5, 3→4).
13-4-4 Vodárna (11 bodů)
Poté, co jste pomohli v jednom nejmenovaném městě vyřešit problém s kanalizací, obrátili se na vás představitelé vodárenské společnosti Velká voda, abyste jí pomohli s následujícím problémem: Rada města rozhodla, že s platností od 29. února 2002 bude muset téci z vodovodních kohoutků voda s malinovou příchutí. Proto je třeba urychleně vystavět továrnu na výrobu malinové šťávy a vyrobenou šťávu přidávat do rozváděné vody. A navíc je podnik třeba postavit na takovém místě, aby šťáva dotekla do všech míst v rozvodné síti. Vaším úkolem je rozhodnout, kde má být podnik postaven.
Váš program dostane na vstupu popis vodovodní sítě – počet uzlů v síti N a poté seznam propojení těchto uzlů. Každé propojení je charakterizováno čísly dvou uzlů, které propojuje, přičemž voda v síti teče od prvního ke druhému uvedenému uzlu. Vaším úkolem je nalézt takový uzel, ze kterého jsou po směru toku vody dosažitelné všechny ostatní uzly v síti (popřípadě říci, že takový uzel neexistuje).
Příklad: Počet uzlů v síti je 8. Propojení vedou takto: 1→8, 8→5, 5→1, 7→5, 8→2, 6→2, 2→4, 4→3, 3→6.
Továrnu je možno postavit v uzlu 7.
13-4-5 LISP (10 bodů)
Náš Lispovský seriál pokračuje, tentokráte grafovou úlohou. Nejprve si ale ukážeme, jak orientované grafy (to znamená množiny vrcholů spolu s množinami šipek mezi nimi) v Lispu elegantně reprezentovat. Provedeme to takhle: ke každému vrcholu si vytvoříme seznam, jehož první prvek bude obsahovat číslo vrcholu (to proto, abychom mohli nějak vrcholy vypisovat a také aby tyto seznamy nemohly nikdy být prázdné) a ostatní prvky budou odpovídat vrcholům, do nichž vede z popisovaného vrcholu hrana, lépe řečeno tyto prvky budou rovnou obsahovat seznamy odpovídající příslušným vrcholům. (Uvědomte si, že v Lispu může být seznam klidně prvkem jiného seznamu a když na to přijde, tak i více takových.)
Ukážeme si to na příkladu. Graf
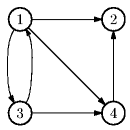
uložíme jako:
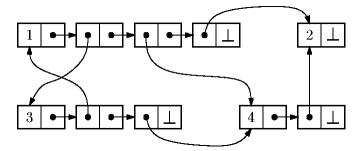
(obdélníčky odpovídají consům, jejich poloviny složkám a a b,
šipky tomu, co v které složce je uloženo a „uzemnítka“ jsou nily).
Takovouto cyklickou strukturu bohužel nelze zapsat přímo, můžeme ji ale
snadno vytvořit například takto:
(set 'v1 (list 1))
(set 'v2 (list 2))
(set 'v3 (list 3))
(set 'v4 (list 4))
(setb v1 (list v3 v4 v2))
(setb v3 (list v1 v4))
(setb v4 (list v2))
A nyní již slíbená úloha. Napište funkci (path v w), která pro dané dva
vrcholy v a w v nějakém orientovaném grafu nalezne nejkratší cestu z v
do w a vrátí seznam čísel vrcholů na této cestě ležících, případně nil,
pokud žádná taková cesta neexistuje. Pro náš ukázkový graf by tedy (path v3 v2)
bylo (3 4 2), zatímco (path v2 v1) vrátí nil.
Pokud si své programy chcete vyzkoušet, můžete si stáhnout interpret Ksp-Lispu (tar, ZIP).