Druhá série čtrnáctého ročníku KSP
Řešení úloh
14-2-1 Kyvadlo (Zadání)
Většina řešitelů se rozhodla cestu provázku prostě nasimulovat. Tento algoritmus si v každém kroku pamatuje délku zbylé části provázku, poslední zpracovaný kolík A a směr, ve kterém jsme do něj přišli. Pak mezi všemi kolíky, na které dosáhneme z A se zbylou částí provázku (s výjimkou A samotného), hledáme ten kolík B, který je z nich nejvíce vlevo vzhledem ke směru, ve kterém jsme přišli do A. Pokud je takových víc, vybereme ten vzdálenější od A. Délku zbylé části provázku zkrátíme o vzdálenost kolíků A a B a postup opakujeme, tentokrát ale za kolík A budeme považovat nalezený kolík B. Algoritmus končí, jakmile z aktuálního kolíku nedosáhneme na žádný jiný.
Tento algoritmus zřejmě řeší úlohu, protože přesně simuluje pohyb provázku, je konečný, protože v každém kroku se zmenší délka zbylé části provázku. Časová složitost je O(KN), kde N je počet kolíků a K je celkový počet „zalomení“ provázku okolo kolíků, protože v každém z K kroků musíme projít všechny ostatní kolíky. Paměťová složitost je O(N), protože právě tolik místa je třeba na uložení pozic všech kolíků.
My si zde ukážeme dvě zlepšení tohoto řešení, díky nimž bude časová složitost v nejhorším případě O(N2). Zaprvé nebudeme opakovaně počítat pořád to samé a ke každému kolíku si budeme pamatovat jeho „následníka“. Jestliže přijdeme do některého kolíku a na jeho následníka už nedosáhneme, provedeme „opravu“ a najdeme nového následníka v dosahu. Podle tohoto algoritmu uděláme celkem K kroků po „cestě“ mezi kolíky, každému z až N kolíků najdeme poprvé následníka v čase O(N).
Ještě spočítáme, kolikrát budeme následníka „opravovat“. V případě, že hledáme nového následníka ke kolíku A, protože jeho starý následník B je moc daleko, víme, že do kolíku B se už nikdy nedostaneme (neexistuje kratší cesta než po přímce), tedy kolík B navždy vypadává ze hry. Proto se při každé „opravě“ následníka počet „použitelných“ kolíků zmenší o jedna, tedy oprav bude nejvýše O(N), každá z nich trvá O(N). Časovou složitost jsme tedy zlepšili na O(N2 + K).
Druhé zlepšení taktéž eliminuje opakované výpočty. Je-li totiž provázek dost dlouhý na to, aby kolem kolíků „oběhl“ několikrát, tak náš algoritmus otrocky počítá každý krok. Tomu se vyhneme tak, že si ke každému kolíku poznamenáme délku zbylé části provázku v době, kdy jsme jej navštívili naposledy. Pokud se pak do tohoto kolíku vrátíme, můžeme snadno zjistit, jak dlouhý byl tento „cyklus“. Místo abychom tento cyklus opakovali, pak můžeme prostě zbylou délku provázku zkrátit o největší možný násobek délky cyklu. Tím získáme délku provázku, která je menší, než délka tohoto cyklu, tedy alespoň jeden z kolíků na tomto cyklu už dále nebude dosažitelný. Proto takových cyklů objevíme O(N). Protože objevení jednoho cyklu nastane nejdéle po N krocích, je celkový počet kroků nejvýše O(N2).
Pro pořádek zrekapitulujme všechny členy výsledné časové složitosti: hledání prvního následníka ke každému kolíku bude trvat O(N2), všechny „opravy“ dohromady O(N2), všechny „kroky“ po kolících celkem O(N2). Výsledná časová složitost je evidentně O(N2).
Ještě bychom měli dokázat věc, kterou jsme používali při zlepšeních: totiž že si údaje (následníka a „čas“ poslední návštěvy) můžeme pamatovat ke každému kolíku a že tyto údaje nezávisí na tom, kterým směrem jsme do daného kolíku přišli (jinými slovy, v daném „cyklu“ se každý kolík vyskytuje právě jednou). Pokud si rozmyslíme případ tří kolíků na jedné přímce, zjistíme, že toto tvrzení neplatí. To ale můžeme snadno „opravit“: všechny vektory od daného kolíku A rozdělíme na dvě části tak, že opačné polopřímky s počátečním bodem A nikdy „nespadnou“ do stejné části a údaje si budeme pamatovat podle toho, z které části jsme přišli do kolíku A. Dá se již dokázat, že údaje si můžeme pamatovat pro každou dvojici kolík-část.
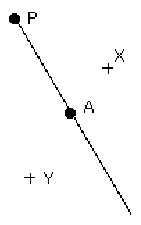
Pomůžeme si obrázkem. Nechť jsme do kolíku A přišli z kolíku P. Pak víme, že v polorovině PAX (s výjimkou přímky PA) není žádný kolík dosažitelný z A (jinak by byl dosažitelný i z P). Následující kolík B tedy musí být v polorovině PAY, a to buď mimo přímku PA, nebo na ní.
Jestliže B je mimo přímku PA, jsou všechny kolíky dosažitelné z A v úhlu BAP (včetně hraničních polopřímek), do kolíku A tedy můžeme znovu přijít jedině z tohoto úhlu. Pokud ale přijdeme z tohoto úhlu, je kolík následující po A kolík B, tedy jsme si jej zapamatovali správně.
Zbývá případ, kdy B je na přímce PA. Jestliže B leží na polopřímce AP, není co řešit, protože existuje jediný směr, jak můžeme přijít do A. Problém nastává právě v situaci, kdy B leží na polopřímce opačné k AP, kdy můžeme do bodu A přijít z bodu P nebo B a pokaždé máme jiného následníka. Protože jsme ale vektory od A rozdělili tak, že opačné polopřímky nejsou v jedné části, pamatujeme si pro každý z těchto směrů následníka zvlášť a nic jsme tedy nepokazili.
Ještě pár slov k technické realizaci, protože analytická matematika je
oblastí, kde se často programuje poměrně obtížně, i když to tak ze zadání
nevypadá. Při hledání kolíku „nejvíce vlevo“ od kolíku A bychom
mohli určit úhel spojnice AK, kde K je zkoumaný kolík, od směru,
kterým jsme přišli. K tomu se výborně hodí funkce atan2(double y, double x),
která spočítá arctan y/x, ale ošetřuje
případy, kdy x = 0, a podle znamének parametrů umístí výsledný úhel
do správného kvadrantu.
Můžeme ale postupovat jednodušeji: budeme hledat kolíky, které jsou vlevo od směru, ve kterém jsme přišli, a zároveň jsou vpravo od našeho dosud nejlepšího kandidáta na následující kolík. To, jestli jde vektor v nalevo nebo napravo od vektoru u, zjistíme jednoduše pomocí vektorového součinu: Budeme-li u a v považovat za vektory v prostoru, bude souřadnice z součinu u ×v menší než, větší než, resp. 0 podle toho, jestli je v vpravo nebo vlevo od u, resp. jestli jsou u a v rovnoběžné. Jsou-li u1, u2 souřadnice vektoru u a v1, v2 souřadnice vektoru v, pak hledaná souřadnice z jejich vektorového součinu je u1·v2 - u2·v1.
Poslední poznámka: počítání s čísly v plovoucí řádové čárce není přesné, takže je vhodné dát procesoru trošku „volnost“ ve výsledku, např. místo zjišťování, jestli je výsledek rozdílu 0 zjišťovat, jestli absolutní hodnota rozdílu je menší než zvolená (zvolená tak malá, že nenulový rozdíl tak „nemůže“ vyjít).
14-2-2 Cenzoři (Zadání)
V této úloze bylo potřeba řešit dva základní problémy – jednak zakázaná slova najít,
a pak je nějak chytře odstranit – a to celé pokud možno co nejrychleji. Okamžitě se
nabízí řešení používající funkce pos a delete v Pascalu, resp. strstr a strcpy v C, ale
s jeho efektivitou to bude špatné – funkce pos pracuje v čase O(n·m), kde n je délka
textu a m je délka slova, funkce delete v O(n). Uvážíme-li, že „počet odstranění“
může být až n/m (všechna slova stejně dlouhá, resp. n pro nestejně dlouhá), dává nám to
složitost O(n/m·(wnm + n)) = O(wn2), kde w je počet slov. Jinými slovy, takové řešení si
asi jedenáct bodů nezaslouží.
Zkušení řešitelé si buď pamatovali, nebo v ročence (úloha 12-2-1) či jiné moudré knize
(aspoň podle toho, co do řešení napsali) našli algoritmus na řešení prvního problému
pracující v čase O(n+wm), což je o hodně lepší než O(nwm) pro funkci pos. Tento algoritmus
zde popisovat nebudu, neboť je již popsán u zmíněné úlohy (tak proč nosit dříví do lesa)
a navíc konečným automatům a jejich konstrukci byla věnována pokračovací série osmého
ročníku KSP.
Zbýva tedy jen dořešit, jak provádět vyškrtávání cenzurovaných slov – jednoduchý algoritmus
typu najdi slovo, vyšktrni a začni zase od začátku vede na složitost O(n2/m), což stále
ještě není to pravé. Pokud si uvědomíme, jak vyhledávací automat pracuje, zjistíme, že po
odstranění slova akorát potřebujeme změnit jeho stav na stav, v němž byl předtím, než začal
číst odstraněné slovo a pokračovat dalšími znaky ve vstupu. Řešení je tedy jednoduché –
pamatujeme si načtené nešktrnuté znaky, a pro každý z nich také stav, v němž se ocitl automat
po jeho načtení. Pokud zjistíme, že jsme právě „donačetli“ zakázané slovo, jednoduše odstraníme
posledních k znaků (k je délka slova) a pak nastavíme aktuální stav na stav u posledního
z neodstraněných znaků. Tím se vyhneme zbytečnému kopírování zbytku řetězce, které provádí
delete.
Časová složitost celého algoritmu pak je O(n+wm+d), kde d je počet odstraněných znaků, protože ale každý znak může být odstraněn nejvýše jednou, je celková složitost O(n+wm).
14-2-3 Dekomprese (Zadání)
Všechna řešení, co jsme obdrželi, byla založena na dekompresi zakódovaného textu, případně jeho částečné dekompresi, a spočítání počtu výskytů hledaného znaku v původním (nezakomprimovaném) textu. Takováto řešení však nejsou polynomiální ve velikosti vstupu, neboť původní (nezakomprimovaný) text může být až exponenciálně větší.
Naše řešení nebude vůbec vytvářet původní text. Nejprve si úlohu malinko zobecněme: LZW kód je tvořen posloupností bloků tvořených buď jedním písmenem nebo odkazem na úsek v předchozím textu. My každému bloku přiřadíme váhu w, která bude udávat, že jeden výskyt hledaného písmene v daném bloku se bude počítat jako w výskytů. Samotný algoritmus na určení počtu výskytů hledaného písmena v textu by mohl vypadat následovně: Uvažme poslední blok LZW kódu. Pokud je tento blok tvořen písmenem, potom ho z kódu odebereme a pokud je písmeno tohoto bloku hledaným písmem, zvýšíme čítač výskytů hledaného písmene o váhu tohoto bloku. Pokud je tento blok odkazem do předchozího textu, pak zvýšíme o váhu posledního bloku váhu těch bloků kódu, které přesně tvoří interval, na který se poslední blok odkazuje. K tomu, abychom mohli zvýšit váhu přesně těch bloků, co tvoří interval, na který se poslední blok odkazuje, může být nutné některé bloky v kódu rozdělit. Nyní by se mohlo zdát, že jsme si příliš nepomohli, neboť nám může vznikat nekontrolovatelné množství nových bloků v kódu.
V našem řešení budeme postupovat tak, jak jsme si výše popsali, ale s trochou opatrnosti navíc. Bloky původního kódu a skupiny bloků vzniklých rozdělením jednoho bloku původního kódu budeme nazývat pravé bloky. V každém kroku našeho algoritmu vezmeme poslední pravý blok (v některých krocích vezmeme skupinu bloků vzniklých rozdělením jednoho pravého bloku) a ty „přičteme“ ke zbylému kódu. Nechť P je počet pravých bloků a Q je počet bloků v našem kódu. V každém kroku se P zmenší o 1. Řekněme, že poslední pravý blok je ve skutečnosti tvořen k bloky. V tomto kroku nejprve snížíme Q o k a pak se možná počet bloků zvýší o k+1 rozdělením některých bloků v kódu. Celkově se tedy Q, počet bloků kódu, zvýší nejvýše v jednom kroku o 1. Protože kroků našeho algoritmu je tolik, kolik je délka původního kódu, délka kódu (měřena počtem jeho bloků), se kterým pracujeme, nikdy nepřevýší dvojnásobek délky kódu zadaného na vstupu. Každý krok algoritmu lze snadno provést v lineárním čase v délce právě zpracovávaného kódu. Časová složitost našeho algoritmu tedy bude O(N2) a jeho paměťová složitost bude O(N), kde N je počet bloků LZW-kódu na vstup. Všimněte si, že délka samotného textu může být až řádově 2N, tj. náš algoritmus může být až exponenciálně rychlejší než algoritmus založený na dekompresi zadaného textu.
Samotný program je přímým přepsáním výše popsaného postupu. Kód je uchováván
v proměnných speciálního datového typu lzw typu záznam. Nejdříve
v proceduře vstup načteme kód (přidržujeme se formátu vstupu v zadání
úlohy) a pomocí funkce redukce odebíráme poslední pravý blok.
Funkce redukce vrací počet výskytů (vzhledem k váhám bloků) hledaného
písmene v odebraných blocích. Pokud dochází k rozdělení
bloku, dodržujeme pravidlo, že první (odkazový) blok pravého bloku má
v položce pismeno hodnotu #0 a ostatní odkazové bloky tohoto
pravého bloku mají v položce pismeno hodnotu #1. Bloky
odpovídající jednomu písmenu není potřeba nikdy rozdělovat, neboť délka
jim odpovídajícího textu je jedna.
14-2-4 Seznamování (Zadání)
Napriek tomu, že tento príklad nie je obtiažny, prišlo relatívne málo riešení. Ideou algoritmu je postupne premiestňovať účastníkov, ktorí majú vo svojej skupine viac známych, do druhej skupiny. Toto sa opakuje pokiaľ existuje účastník, ktorý má v druhej skupine menej známych. Z popisu ešte nie je zrejmé, či sa tento algoritmus nezacyklí na nejakom vstupe, preto to musíme dokázať.
Nech F je počet dvojíc, ktoré sa poznajú a sú v jednej skupine v nejakom rozdelení. Na začiatku nech sú všetci účastníci v prvej skupine, teda F0 je M (počet známostí). Každým presunom sa hodnota F zmení na F-k+(p-k), kde p je počet známych presúvaného účastníka a k je počet jeho známych v pôvodnej skupine. Pretože F je shora obmedzená a p - 2k je záporné číslo (vybrali sme účastníka pre ktorého platí 2k > p), bude F klesať až sa raz zastaví. Potom musí platiť, že neexistuje niekto kto pozná vo svojej skupine viac účastníkov (inak by sme ho ešte mohli preradiť). Časová zložitosť algoritmu je O(mn), pamäťová O(m+n), kde m je počet známostí a n počet účastníkov.
14-2-5 Turingovy stroje (Zadání)
K řešení této úlohy se dá přistoupit dvěma způsoby. Oba dva vedou stroj, který pracuje v čase i prostoru O(N). První způsob bude využívat stroj se třemi páskami. První dvě pásky budeme používat jako pomocné, na třetí pásce si zkonstruujeme číslo ve dvojkové soustavě a to nakonec překopírujeme na první pásku. Číslo ve dvojkové soustavě budeme konstruovat tak, že budeme postupně procházet přes jedničky na první pásce, každou druhou jedničku si zapíšeme na druhou pásku a na třetí pásce si budeme průběžně udržovat počet projitých jedniček modulo dva. Když dojdeme na konec jedniček na první pásce (řekněme, že jich tam bylo k), máme na třetí pásce k mod 2 a na druhé pásce k / 2. Nyní smažeme číslo na první pásce, nakopírujeme na jeho místo číslo z druhé pásky a pak znovu procházíme posloupnost jedniček na první pásce (mohli bychom se pokusit stroj zrychlit tak, že bychom místo kopírování pouze zaměnili význam první a druhé pásky. To by nám ale žádné asymptotické zrychlení nepřineslo, a proto si touto optimalizací nebudeme komplikovat život). Takto postupujeme dokud na první pásce zbývají nějaká čísla. Nakonec ještě překopírujeme výsledek z třetí pásky na první. Časová složitost našeho Turingova stroje je O(N+N/2+N/4+…+1)=O(N), jeho paměťová složitost je zřejmě O(N+N/2+ log N)=O(N). Implementace tohoto stroje je čistě technickou záležitostí, a proto ji zde neuvádíme.
Druhý způsob má výhodu v jednodušší implementaci, ovšem jeho nevýhodou je komplikovanější analýza časové složitosti. Tento způsob využívá stroje se dvěma páskami. Z první pásky se vstupem budeme postupně odebírat jedničky a ty budeme přičítat k číslu ve dvojkové soustavě uloženému na druhé pásce. Přičítání jedničky k číslu ve dvojkové soustavě je jednoduché. Procházíme číslo od nejnižších bitů. Dokud jdeme po jedničkách přepisujeme je na nulu (dochází totiž k přenosu). Když narazíme na nulu nebo na Λ, přepíšeme ji na jedničku a vrátíme se na začátek čísla. Když nám dojdou jedničky na vstupní pásce, překopírujeme číslo z druhé pásky na první a skončíme. Stroj bude mít zřejmě paměťovou složitost O(N+ log N)=O(N). S časovou složitostí je to ovšem komplikovanější, protože jedno přičtení jedničky nám může trvat až O(log N) a celkově bychom tedy dospěli k času O(N log N). Pokud chceme dosáhnout lepšího odhadu, musíme počítat přesněji – nebudeme počítat, kolik nám trvá jedno přičtení jedničky, ale jak dlouho nám bude trvat nasčítat po jedničce do N (tedy jak dlouho nám bude trvat provedení N operací přičtení jedničky). Můžeme klidně předpokládat, že N=2K (jinak si dané číslo pro účely odhadu můžeme zvýšit na nejbližší vyšší mocninu dvojky – zvýšíme ho tak nejvýše dvakrát a asymptoticky si tedy neuškodíme). Počet operací v posloupnosti N přičítání, které se zastaví na první cifře, bude zřejmě N/2 – právě tolik čísel totiž končí na nulu. Obdobně počet operací, které se zastaví na druhé cifře, bude N/4, protože tolik je čísel z 0… N-1, která končí na jedničku a na druhé cifře od konce mají nulu. Takto snadno spočteme, že počet operací, které projdou i cifer, bude N/2i. Když nyní čas pro všechny operace sečteme, získáváme sumu:
| K |
| i=0 |
| K |
| i=0 |
(První z nerovností plyne z následujícího rozpisu sumy)
| K |
| i=0 |
| K |
| i=0 |
| K |
| i=1 |
| K |
| i=K |
ve kterém se j-tá suma dá shora odhadnout jako 1/2j.
Poznámka: Takovémuto počítání složitosti celé posloupnosti operací se říká „amortizovaná složitost“.
Stroj pro postupné přičítání:
| (q0,(Λ,Λ)) | → (q0,(0,Λ),(L,L)) | Ošetříme prázdný vstup |
| (q0,(1,Λ)) | → (q1,(0,Λ),(R,R)) | Označíme začátky pásek |
| (q1,(?,Λ)) | → (q2,(?,1),(N,N)) | Zapíšeme první nabranou jedničku |
| (q2,(1,?)) | → (qi,(Λ,?),(R,N)) | |
| (q2,(Λ,?)) | → (qc,(Λ,?),(L,N)) | Došli jedničky na vstupu? |
| (qi,(?,1)) | → (qi,(?,0),(N,R)) | Procházíme přes jedničky |
| (qi,(?,0/Λ)) | → (qv,(?,1),(N,L)) | Konec přetékání? |
| (qv,(?,0)) | → (qv,(?,0),(N,L)) | Návrat na počátek |
| (qv,(?,1)) | → (qv,(?,1),(N,L)) | Návrat na počátek |
| (qv,(?,Λ)) | → (q2,(?,Λ),(N,R)) | |
| (qc,(Λ,?)) | → (qc,(Λ,?,(L,N)) | Návrat na první pásce |
| (qc,(0,x)) | → (qc',(x,Λ),(R,R)) | Začínáme kopírovat z druhé pásky |
| (qc',(Λ,x)) | → (qc',(x,Λ),(R,R)) | |
| (qc',(Λ,Λ)) | → (qe,(Λ,Λ),(L,L)) | Dokopírováno |
| (qe,(?,?)) | → (qe,(?,?),(L,L)) | Končíme |