První série patnáctého ročníku KSP
- Termín série: 18. října 2002
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
15-1-1 Narozeninový dort (11 bodů)
Manželé Terciovi měli trojčata – Alfíka, Betynku a Gamíka. Narozeniny byly pro rodiče vždy velmi náročné. Přeci jen shánět dárky hned pro tři děti naráz dá dost práce, a tak se rodiče jednoho roku rozhodli, že si alespoň trochu ulehčí práci a dají dětem dohromady jeden dort. Dort to nebyl ledajaký – měl tvar rovnostranného trojúhelníka a na dortu bylo tolik svíček, kolik měly děti dohromady let. Problém ale nastal, když se dort měl dělit. Každé dítě totiž chtělo mít tolik svíček, kolik mu právem náleží, a svíčky na dortu přitom byly rozmístěny náhodně. Tatínek se pokoušel dort rozdělit, ale brzy zjistil, že splnit požadavek dětí není tak jednoduché, a tak o pomoc požádal vás.
Vaším úkolem je navrhnout algoritmus a napsat program, který dostane na vstupu délku hrany dortu d (rohy dortu mají souřadice [0,0], [d,0], [d/2, d·√3/2]), počet svíček na dortu N (pochopitelně dělitelný třemi) a souřadnice jednotlivých svíček a nalezne na dortu bod takový, že řezy z jednotlivých rohů do nalezeného bodu rozdělí dort na tři části obsahující stejný počet svíček.
Příklad: Pro dort o délce hrany 10 a souřadnicích 3 svíček (1,1), (9,1) a (5,1) je hledaným bodem například bod o souřadnicích (5,3).
15-1-2 Vláčky (11 bodů)
Vlastík měl doma postaveno velké kolejiště. Na kolejišti vedlo vedle sebe několik kolejí, které se mezi sebou složitě proplétaly (Vlastík při stavbě nešetřil ani nadjezdy a tunely), spojovaly se a zase se dělily. Jednoho dne Vlastíka napadlo spočítat, kolik vlaků může na kolejiště vypustit současně. Po chvilce zjistil, že problém to není vůbec jednoduchý, a tak se rozhodl si při řešení úlohy pomoci programem. Pomůžete mu s ním?
Vaším úkolem je navrhnout algoritmus a napsat program, který dostane na vstupu popis kolejiště a na výstup vypíše maximální možný počet tras, které se navzájem neprotínají (tzn. nemají žádný společný bod), spolu s jejich popisem. Kolejiště se skládá z N kontrolních bodů. i-tým kontrolním bodem vede ki kolejí. Dále je dán seznam kolejí mezi jednotlivými kontrolními body – j-té propojení mezi dvěma kolejemi v kontrolních bodech je popsáno dvěma dvojicemi (aj, bj), (cj, dj), kde aj a cj jsou čísla kontrolních bodů, mezi kterými kolej vede (předpokládejte, že cj=aj+1) a bj a dj jsou čísla kolejí v jednotlivých kontrolních bodech. Protože v kontrolních bodech se mohou vyskytovat výhybky, může být na jednu kolej v kontrolním bodě napojeno hned několik kolejí v předcházejícím a následujícím kontrolním bodě (ale nemusí být napojena kolej žádná). Předpokládejte, že koleje se stýkají či dělí pouze v kontrolních bodech a mezi body se koleje neprotínají (to ovšem neznamená, že jedna kolej nepřejíždí druhou po nadjezdu).
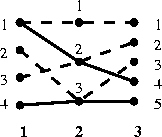
Příklad: Pro kolejiště se třemi kontrolními stanovištěmi se 4, 3 a 5 body a s propojeními (1,1)→(2,1), (1,1)→(2,2), (1,2)→(2,3), (1,3)→(2,2), (1,4)→(2,3), (2,1)→(3,1), (2,2)→(3,2), (2,2)→(3,4), (2,3)→(3,3) a (2,3)→(3,5) existují tři neprotínající se trasy. Jsou to například (1,1)→(2,1)→(3,1), (1,2)→(2,3)→(3,3) a (1,3)→(2,2)→(3,2).
15-1-3 Kulový blesk (10 bodů)
Stěhovací firma Popruh a spol. se rozhodla uspořádat propagační akci Kulový blesk. Akce spočívá v tom, že N rodin si vymění byty takovým způsobem, že pokud rodina bydlela v bytě i, tak po stěhování bude bydlet v bytě i+1 (pokud rodina bydlela v bytě N, tak bude po stěhování bydlet v bytě 1). Zorganizovat takovou směnu je samozřejmě velmi náročné, a tak se firma rozhodla ji trochu zjednodušit. Výměna bude probíhat tak, že se dohodnou vždy dvojice rodin a ty si vymění byty (současně může probíhat libovolně takovýchto výměn najednou, ale každá rodina se v daném okamžiku může účastnit nejvýše jedné směny). Tento způsob má ale tu nevýhodu, že některé rodiny se budou muset stěhovat vícekrát, než se dostanou do kýženého cílového bytu. Protože celou výměnu by bylo vhodné provést v jeden den, chce pan Popruh v rámci zachování dobrého jména firmy minimalizovat dobu nutnou na stěhování. Nakonec se rozhodl obrátit na vás, abyste mu se svou znalostí programování pomohli naplánovat výměny bytů.
Váš program dostane na vstupu počet bytů N. Stěhování, které má program navrhnout, má probíhat tak, že v jednom okamžiku si vždy nějaké dvojice rodin vymění byty (jeden takovýto okamžik záměny nazveme „fází“). Váš program by tedy měl vypsat počet fází a pro každou fázi seznam dvojic bytů, které jsou v této fázi směněny. Navržené stěhování by mělo mít nejmenší možný počet fází.
Příklad: Pro čtyři rodiny lze stěhování provést na dvě fáze. V první fázi se vymění rodiny v bytech (1,2) a (3,4) a ve druhé fázi rodiny v bytech (1,3).
15-1-4 Soustavy (8 bodů)
Vaším úkolem v této úloze je navrhnout algoritmus a napsat program, který dostane
na vstupu tři čísla (či spíše řetězce složené ze znaků 0 až 9 a a až z)
A, B a C a určí základ soustavy, ve které platí rovnice A+B=C. Pokud
základ soustavy není jednoznačně určen, vypište soustavu s nejmenším základem,
která rovnici vyhovuje.
Příklad: Pro A=1, B=1a a C=20 je základ soustavy 11.
15-1-5 Haskell (10 bodů)
V letošní sérii se budeme zabývat funkcionálním programováním. Cílem je zejména vyvrátit obecně rozšířenou představu, že funkcionální programování = LISP = umění správně spočítat závorky. Pro účely výkladu (a také úloh pro vás) budeme používat programovací jazyk Haskell. Jedná se o poměrně komplikovaný jazyk a není v našich možnostech probrat ho celý; v následujícím textu si vyložíme alespoň jeho základy.
Pro řešení semináře by vám měl postačovat interpreter Hugs
(http://www.haskell.org/hugs/). Pokud byste chtěli v Haskellu
sepsat nějaký seriózní program, existuje kompilátor GHC
(http://www.haskell.org/ghc/). Kompletní specifikaci jazyka si můžete
přečíst například na http://www.haskell.org/definition/. Jsem ovšem
v pokušení vypsat prémiové body za její pochopení.
Haskell je čistě funkcionální typovaný líně vyhodnocovaný jazyk. Co to všechno znamená?
- „Čistě funkcionální“ znamená, že celý program je skutečná funkce; tedy že
nemají žádné vedlejší efekty (za vedlejší efekty považujeme například
vstupy a výstupy, zápisy do globálních proměnných a podobně – tedy všechno to,
co způsobuje, že
f(x) + f(x)se nemusí chovat stejně jako2*f(x)). To vypadá dost podivně – k čemu by byl programovací jazyk, ve kterém nejde například cokoliv vypsat na obrazovku? Jak je toto vyřešeno si povíme v některé z následujících sérií. Výhoda tohoto přístupu je v tom, že je mnohem snazší uvažovat o tom, co vlastně program dělá – víme, že to nemůže být ovlivněno ničím jiným, než parametry funkce. Navíc to překladači umožňuje provádět optimalizace, které by v jiných jazycích byly neproveditelné bez obtížné meziprocedurální analýzy. - „Typovaný“ znamená, že všechny výrazy a funkce mají přesně daný typ, který se kontroluje v době překladu. To má své výhody (odchytí se tím mnoho chyb a není potřeba kontrolovat typy za běhu programu – nemůže se nám stát, že bychom se omylem pokusili sečíst číslo a řetězec), ale i své nedostatky (v čistém Haskellu nelze právě z důvodu typování vytvořit heterogenní seznam – tj. takový, který by obsahoval například řetězce a čísla zároveň). Typový systém Haskellu je velmi flexibilní, jak uvidíme dále, ale je i velmi bezpečný vzhledem k tomu, že neexistuje přetypování (dokonce nelze přímo provést ani takovou „samozřejmost“, jako sečíst reálné a celé číslo).
- „Líný“ se vztahuje k tomu, že vyhodnocovány jsou jen ty výrazy, které
jsou potřeba, a to až tehdy, když jsou potřeba (dá se říci, že všechny funkce
v Haskellu se chovají jako special formy v LISPu). Mějme například následující
definici (definující funkci
constse dvěma argumenty, která vrací první z nich – dá se to ovšem také chápat tak, že je to funkce s jedním argumentemx, která vrací konstantní funkci (s jedním argumentemy, který ignoruje), jejíž hodnota je vždyx):const x y = xPak
const 5 (error "Chyba")vrátí5– druhý argument, který by ukončil program s chybou, se vůbec neprovede! Dále to znamená, že můžeme při výpočtu používat jeho výsledek, pokud tím nedojde k „zacyklení“ – viz následující příklad:natural = 1 : map (+1) naturalToto je definice posloupnosti 1, 2, 3, … – její první člen je 1 a za ním následuje tatáž posloupnost zvětšená o 1. Tento program skutečně funguje, neboť první člen posloupnosti známe a abychom zjistili hodnotu n-tého členu posloupnosti, potřebujeme znát pouze hodnotu n-1. členu.
Nyní se podívejme podrobněji na systém typů. Asi nejjednodušší bude začít příkladem:
data List x = Cons x (List x) |
Nil
Tato definice deklaruje typ List x, což je seznam prvků typu x. Seznam
je tedy buď prázdný (konstanta Nil), nebo je to dvojice, jejíž první
prvek je typu x (tj. první prvek seznamu) a druhý prvek je seznam prvků
typu x (zbytek seznamu). Například seznam 1, 2, 3 je vyjádřen jako
Cons 1 (Cons 2 (Cons 3 Nil)). Cons a Nil jsou
konstruktory; tedy funkce, které vytváří hodnoty daného typu. Cons má za
argumenty hlavu a tělo seznamu, zatímco Nil je funkce bez argumentů
(tedy konstanta).
Věci, které stojí za povšimnutí:
- Jména typů (v našem případě
List) a konstruktorů (ConsaNil) začínají velkým písmenem. - Jména typů a konstruktorů nemusí být různá (nemůže dojít k záměně, protože typy se nemohou nikdy vyskytovat ve výrazech). To se často využívá, zejména tehdy, má-li typ jen jeden konstruktor.
- Typy mohou být parametrizovány. V našem případě jsme nadefinovali typ
List x, což je seznam prvků typux. Zaxlze dosadit libovolný typ. Například uvedený seznam čísel by měl typList Int. Lze ovšem také vytvořit funkce, které budou pracovat nad takto obecným typem (například u funkce vracející délku seznamu je jedno, jaký typ mají prvky tohoto seznamu). - Typy mohou být rekurzivní – v definici seznamu jsme použili právě definovaný typ.
Haskell má některé základní typy:
Intje typ pro celá čísla; konstanty tohoto typu se zapisují běžným způsobem (čísla v desítkové soustavě).Charje typ pro znaky; znakové konstanty se uváději v apostrofech:'a'.Boolje typ pro logické hodnoty; může nabývat hodnotTrueneboFalse.()je jednotkový typ – obsahuje právě jen hodnotu()(používá se tehdy, jestliže chceme například deklarovat funkci, která nic nevrací (tedy proceduru))(a,b)je typ pro dvojici (jejíž první prvek má typaa druhýb). Analogicky(a,b,c)pro trojice, atd.(5,'a')je příklad konstanty typu(Int,Char).[a]je typ pro seznam prvků typua. Jeho definice přesně odpovídá výše uvedenému typuList, pouze místoNilse používá[]a místoConsdvojtečka. Dále lze použít i seznam prvků v hranatých závorkách (tedy seznam 1, 2, 3 lze zapsat jako1:2:3:[]nebo jako[1,2,3])Stringje typ pro řetězce (je identický s[Char]). Konstanty tohoto typu lze uvádět v uvozovkách (tedy"abc"=['a','b','c']='a':'b':'c':[]).
Zbývá ukázat, jak vypadají typy funkcí. Funkce, která má jeden parametr typu
a a vrací hodnotu typu b, má typ a->b. Logická otázka je,
co s funkcemi více parametrů. Odpověd je, že si vystačíme s funkcemi s jedním
argumentem. Například plus má typ Int->(Int->Int) – je to tedy
funkce, která vrací funkci, která vrací Int. plus 5 je tedy
funkce typu Int->Int (která vrací argument zvětšený o 5), a
(plus 5) 10 je 15. Typy funkcí se závorkují vždy zprava, zatímco
jejich aplikace zleva – tedy závorky v uvedeném příkladu jsou zbytečné,
plus má typ Int->Int->Int a pro jeho vyhodnocení stačí napsat
plus 5 10. Pozor – funkce jsou hodnoty jako každé jiné (je možné
je dávat jako parametry jiným funkcím, je možné mít typ [a->b] –
seznam funkcí, atd.)
Typy funkcí není potřeba uvádět – překladač si je domyslí. Je ovšem rozumné to dělat (snáze se pak odhalí chyby). Deklarace typu funkce vypadá takto:
length :: [a]->Int
Jak jsme již viděli na příkladech, program v Haskellu je množina rovností definujících funkce. Na konci zadání si můžete prohlédnou rozsáhlejší příklad demonstrující podmnožinu Haskellu nutnou pro rozumnou práci.
Několik poznámek k programům:
- - - začínají komentář. Ten končí na konci řádky.
- Jména funkcí a parametrů začínají malým písmenem. Jejich součástí může
být apostrof; pozor, pojmenovat si cokoliv
x''''''''nezvýší čitelnost programu. - Aplikace funkcí mají vyšší prioritu než operátory; tj.
delka t + 1se překládá jako(delka t) + 1. - Klauzule
letawherenám umožňují zavádět lokální definice; rozdíl mezi nimi je ten, želet něco in výsledekje výraz, zatímcowherelze uvést pouze za definicí funkce (tohle není tak úplně pravda, ale pro naše účely to stačí). Lze mít víc lokálních definic uvnitř jednoho takového příkazu (uwhereje to vidět i na příkladu), tyto definice mohou být rekurzivní. - K „rozkládání“ strukturovaných typů je možné použít tzv. „pattern matching“;
tj. všude tam, kde se něco přiřazuje (uvnitř
letnebowhere, u parametrů funkcí, …) lze uvést „vzor“ toho, co si představujeme, že dostaneme. Uvnitř tohoto vzoru můžeme mít proměnné, jim jsou pak přiřazeny hodnoty. Pokud to, co přiřazujeme, neodpovídá vzoru, u definice funkce se přechází na následující alternativní definici (je-li nějaká taková), jinak dojde k chybě. Pro znalce Prologu: pozor, nejedná se o unifikaci; pokud ve vzoru použijeme vícekrát jednu proměnnou, je to chyba! - Pro „rozkládání“ struktur navíc slouží příkaz
case; ten má seznam alternativ a vrátí první z nich, jejíž struktura odpovídá. - U příkazu
ifvždy musí býtelsevětev – je to výraz, tedy něco vrátit musí!
Nyní si uvedeme ještě několik užitečných funkcí definovaných ve standardní knihovně. U funkcí uvádíme i jejich typy (pro zjednodušení většinou jinak, než jak jsou skutečně definované):
==, /=, <, >, <=, >= :: Int->Int->Bool- - porovnávání čísel+, -, *, div, mod :: Int->Int->Int- - aritmetikamin, max :: Int->Int->Int- - minimum a maximum dvou číselminimum, maximum :: [Int]->Int- - minimum a maximum (neprázdného) seznamu&&,||:: Bool->Bool->Bool,not::Bool->Bool- - logické operace and, or, notfst :: (a,b)->a, snd :: (a,b) -> b- - první a druhý prvek dvojice. :: (b->c)->(a->b)->(a->c)- - skládání funkcí$ :: (a->b)->(a->b)- - nedělá nic; umožnuje nám psát napříkladmin 1 $ min 2 $ min 3 4místomin 1 (min 2 (min 3 4))(viz pravidla pro závorkování).error :: String -> a- - vypíše chybu a pak ukončí programhead,last :: [a]->a,tail::[a]->[a]- - první a poslední prvek seznamu, seznam po odtržení prvního prvku++ :: [a]->[a]->[a]- - zřetězení dvou seznamůmap::(a->b)->[a]->[b]- - aplikuje funkci na každý prvek seznamu
A nyní již úlohy pro vás. Mějme typ pro strom definovaný takto:
data Tree a = Tree a [Tree a] deriving (Show)
Tedy strom prvků typu a obsahuje hodnotu typu a a seznam
svých synů, což jsou opět stromy téhož typu (klauzule deriving Show zajistí,
že překladač Haskellu bude umět hodnoty tohoto typu zobrazovat).
- Máme dán strom celých čísel (typu
Tree Int). Napište funkci, která zkonstruuje stejný strom, v němž budou všechny hodnoty nahrazeny minimálním prvkem zadaného stromu.Příklad:
Vstup:
Tree 6 [Tree 2 [], Tree 3 [ Tree 4 [], Tree 5 []]]Výstup:
Tree 2 [Tree 2 [], Tree 2 [ Tree 2 [], Tree 2 []]] - Vaše řešení předchozí úlohy zřejmě obsahuje 2 průchody stromem (jeden na nalezení minima, druhý na konstrukci výsledku). Zkuste vymyslet řešení, které řeší tutéž úlohu jediným průchodem. Rozmyslete si, jak bude počítač toto řešení vyhodnocovat.
Příklad rozsáhlejších programů v Haskellu
delka::[x]->Int - - délka seznamu
delka [] = 0 - - délka prázdného seznamu je 0
delka (h:t) = delka t + 1 - - délka seznamu je jeho délka po odtržení
- - prvního prvku + 1
delka_listu::List x->Int - - totéž, ale pro námi definovaný typ List
delka_listu Nil = 0
delka_listu (Cons h t) = delka_listu t + 1
obrat::[a]->[a] - - obrácení seznamu
obrat l = obrat' l [] - - vyvoláme pomocnou fci obrat'; obrat' l1 kon
where - - vrací obrácený seznam l1, za nějž připojí kon
obrat' [] kon = kon - - je-li l1 prázdný, vrať kon
obrat' (h:t) kon = obrat' t (h:kon)
- - jinak obrať tělo l1, za něj připoj jeho hlavu
- - a kon
radky :: String -> [String] - - rozdělí řetězec na řádky (oddělené znakem '\n')
radky "" = [] - - prázdný řetězec nemá řádky
radky s = let (l, s') = sekni s - - jinak rozsekni s na prvním znaku '\n' (pomocnou
- - fcí sekni); první řádek dej do l, zbytek do s'
in l : case s' of
- - vrať první řádek, za který připoj
"" -> []
- - nic, pokud uz nic nezbýva
('\n':s'') -> radky s''
- - ostatní řádky jinak
where
sekni "" = ("","") - - prázdný řetězec
sekni ('\n':zb) = ("",'\n':zb) - - konec řádku
sekni (x:zb) = let (l, zb') = sekni zb in (x:l,zb')
- - jinak odtrhni první písmeno (x), sekni
- - zbytek (zb) na l a zb' a před l připoj x
mensi::Int->Int->Int - - vrátí menší ze dvou čísel
mensi x y = if x < y then x else y