Třetí série sedmnáctého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 17-3-1: Spisovatel Vilík
- 17-3-2: Popleta Truhlík
- 17-3-3: Starosta Hafák
- 17-3-4: Myslitel Cibulka
- 17-3-5: Jazykozpytcova naděje
17-3-1 Spisovatel Vilík (Zadání)
Nejprve si uvědomíme, že dvě slova (úseky textu) jsou shodná, pokud obsahují stejné počty jednotlivých písmen. Tj. například „ABCAB“ a „AABBC“ jsou stejná, protože obsahují dvakrát A, dvakrát B a jednou C. Nejdříve si tedy pro každé slovo délky k v textu spočítáme, kolik kterých písmen se v něm vyskytuje – tj. každé pozici p v textu přiřadíme 30-tici čísel T(p), udávající počet příslušných písmen v následujících k znacích textu. Přímočaré řešení by všechna T(p) určilo v čase O(kN), kde N je délka textu. Tuto složitost však můžeme snadno zlepšit na O(N), pokud si povšimneme, že T(p+1) se od T(p) liší pouze ve dvou číslech – přibude jeden výskyt písmena na pozici p+k a ubude výskyt písmena na pozici p. Čili můžeme T(p) spočítat postupně od začátku do konce, a na vytvoření každé 30-tice spotřebujeme pouze konstantní množství času.
Nyní zbývá pouze najít první opakování nějaké 30-tice. Jednou z možností je použít hešování (viz kuchařka druhé série). Nevýhodou je to, že lineární časovou složitost nemáme zaručenu, ale dosáhneme jí pouze v průměrném případě, nebo pokud jsme mocní mágové (tj. umíme zvolit správnou hešovací funkci), randomizovaně.
Řešení, které tuto nevýhodu nemá, je si 30-tice setřídit lexikograficky. Pak jsme schopni jedním průchodem najít opakující se 30-tice (v setříděné posloupnosti budou následovat za sebou), a pokud si navíc pamatujeme, kde se v zadaném textu vyskytovaly, je snadné určit první z nich.
K třídění použijeme RadixSort. Podrobně je popsán v kuchařce druhé série minulého ročníku, zde jen zopakujeme základní myšlenku. RadixSort funguje tak, že nejprve setřídíme posloupnost podle poslední složky 30-tice, pak podle předposlední, …, a nakonec podle první, přičemž si dáváme pozor, abychom nezměnili pořadí prvků, které se v dané složce shodují. Není těžké si rozmyslet, že výsledná posloupnost pak bude opravdu setříděná – protože poslední třídění proběhlo podle nejdůležitější složky, a mezi slovy, která se v ní shodují, pak rozhoduje pořadí podle druhé nejdůležitější, atd. Třídění podle i-té složky v lineárním čase zvládneme snadno – prvky rozložíme do k+1 přihrádek podle hodnoty i-té složky, a pak je vybereme od nejmenší k největší. Budeme tedy vybírat k přihrádek, a samotné kopírování hodnot nám zabere čas N, dohromady bude časová složitost na jeden průchod O(N+k) = O(N), a průchodů je konstantně mnoho – 30.
Takto dosáhneme časové složitosti O(N) i v nejhorším případě. Paměťová složitost bude také O(N).
17-3-2 Popleta Truhlík (Zadání)
Problém pana Truhlíka popletl i řadu zkušených řešitelů. Odevzdaná řešení tak byla plná roztodivného zvířectva. Za zmínku určitě stojí housenky složené z příkazů if (then) else, které dosahovaly délky až šestadvaceti řádků. Rovněž šestadvacetihlavá saň switch/case se často snažila řešit problém převodu vstupního slovníku na slovník číselný. Řešení obsahující tyto implementační neduhy však (kromě upozornění v podobě velkého FUJ) nebyla nikterak potrestána, přesto bych takovýmto řešitelům doporučil shlédnout kód vzorového řešení. Co se již však neobešlo bez bodových ztrát, byla řešení s exponenciální složitostí, která po nalezení všech možných vět hledala větu nejkratší. Přitom leckde chybělo málo k tomu, aby časová složitost byla optimální!
Nutno podotknouti, že cest ke zdárnému vyřešení úlohy bylo poměrně mnoho. Stalo se tak hlavně proto, že úlohu bylo možné chápat z několika různých pohledů, z nichž ani jeden se po zralé úvaze nedá označit jako nesmyslný či špatný. Někteří řešitelé se tak zaměřili na provokativně zvolené N (počet telefonních čísel, ke kterým si chce Truhlík zapamatovat větu), jiní se snažili rychlost algoritmu poměřovat především s velikostí vstupního slovníku P.
| n |
| i=1 |
| 2 |
| i |
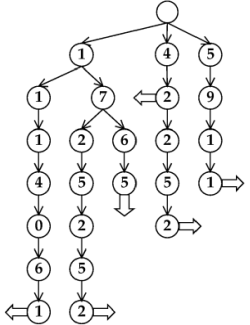
Když už máme takovou trii postavenou, můžeme se zabývat skládáním věty pro telefonní číslo. K tomu budeme ještě potřebovat dvě pole wc a wi, obě délky telefonního čísla. V průběhu algoritmu bude prvek wc[k], pro nějaké k ∈{1, … , Ci}, označovat minimální počet slov, které jsme doposud potřebovali ke složení cifer i1, … , ik telefonního čísla i. Prvek wi[k] pak bude ukazatel na slovo v původním slovníku délky l takové, že číselný řetězec ik-l, ik-l+1, … , ik odpovídá tomuto slovu. Na počátku inicializujeme obě pole nulami, postavíme si před sebe telefonní číslo i a začneme v kořeni trie. Načteme první cifru telefonního čísla. Pokud má kořen trie potomka, který odpovídá cifře i1, přejdeme v trii do tohoto potomka. V případě, že u tohoto potomka je nastaven příznak konce slova, nastavíme wc[1]=1 a wi[1] položíme rovno ukazateli na slovo do původního slovníku, který v tomto vrcholu máme uložen. Poté načítáme další cifry a procházíme trii tak dlouho, dokud to jde, nebo až do chvíle, kdy vyčerpáme celé telefonní číslo. Zároveň pro každý navštívený vrchol trie, který označuje konec slova, nastavujeme hodnoty polí wc a wi. Udělali jsme tedy jeden průchod a všimněme si, že pole wc nyní obsahuje jedničky na těch místech, které odpovídají délkám slov původního slovníku takovým, že začátek telefonního čísla se shoduje s jejich číselnou reprezentací. Nyní přejděme k první nenulové hodnotě wc[j], postavme se opět do vrcholu trie a spusťme celý průchod znovu s tím, že již pracujeme pouze s ciframi j, … , Ci telefonního čísla. V tomto a dalších průchodech již měníme pole wc a wi pouze tehdy, nebylo-li dané pozice v telefonním čísle ještě dosaženo žádnou posloupností slov. Po Ci takovýchto průchodech je zřejmě wc[Ci]=0 právě tehdy, když telefonní číslo nelze složit pomocí slov ze slovníku. Pro jiné hodnoty číslo složit lze a pro složení dobře poslouží právě pole wi. Stačí na konec věty vypsat slovo, na které ukazuje wi[Ci] a posunou se v poli wi na pozici o délku tohoto slova doleva, tam se nalézá předposlední slovo hledané věty atd.
| n |
| i=1 |
| 2 |
| i |
17-3-3 Starosta Hafák (Zadání)
Snadno odhalíme, že hranu nesmíme zjednosměrnit právě tehdy, je-li mostem. Most je totiž hrana, jejímž odebráním se graf rozpadne na dvě komponenty souvislosti. Je tedy jediným spojením mezi těmito dvěma komponentami, a když ho učiním propustným pouze pro jeden směr, tak se dostanu z první komponenty do druhé, ale ne opačně.
Tady nám poslouží algoritmus na hledání mostů z kuchařky, který dá lehce upravit pro naše účely.
Pro každý vrchol v si stejně jako v kuchařce budeme pamatovat, v jaké hloubce vůči kořeni se nachází (kořen v hloubce 0, synové 1, synové synů 2, …) a do jaké nejnižší hladiny se umím dostat z podstromu s kořenem v. Zde se ovšem v kuchařce vyskytla chyba, kterou naštěstí mnozí hravě odhalili. Při hledání spojení do nižší hladiny nesmíme vůbec uvažovat hranu mezi otcem vrcholu v a vrcholem v. Ta totiž způsobí, že cestu do nižší hladiny najdeme vždy (každý vrchol má otce), ale není to kýžená kružnice, nýbrž dvakrát započítaná hrana, po které jsme do vrcholu v přišli. Zrada! Takhle totiž nikdy nenajdeme žádný most.
Pokud se z podstromu s kořenem v (s otcem u) neumíme dostat do hladiny nižší, než je hladina vrcholu v, pak do tohoto podstromu vede jedna jediná hrana, a to hrana (u,v). Ta je tedy mostem, v zájmu propustnosti v obou směrech ji ponecháme obousměrnou.
Pokud se z podstromu s kořenem v (s otcem u) umíme dostat do hladiny nižší, než je hladina vrcholu v, bez použití hrany (u,v), tak jsme právě našli kružnici „u →v → nějaké vrcholy v podstromu v → (vrcholy v nižší hladině než vrchol v, ne nutně) →u“. A kružnici můžeme směle zjednosměrnit, snadno vidíme, že zjednosměrnění kružnice neublíží dosažitelnosti vrcholům na této kružnici, prostě budeme „kroužit“ dokola.
Také si můžeme všimnout, že na této kružnici jsou všechny hrany dopředné, kromě té jediné, která se z hlubší hladiny vrací do nižší, a ta je zpětná.
Nakonec ještě musíme vymyslet, jak sjednotit zjednosměrňování více kružnic. Ale k tomu se stačí dohodnout, že dopředné hrany budeme zjednosměrňovat „dopředu“, čili otec → syn, a zpětné ve směru od vrcholu na hlubší hladině k vrcholu na nižší hladině („dozadu“).
Algoritmus našel všechny mosty a ponechal je obousměrné, našel ale i všechny kružnice a zorientoval je ve shodném směru. Takže jsme nezjednosměrnili nic závadného a naopak jsme zjednosměrnili maximum. Při reprezentaci grafu seznamem následníků získáváme časovou i paměťovou složitost O(N+M).
Škoda, že většinu řešitelů kuchařka sváděla k řešení „pomocí algoritmu z kuchařky odstraním mosty, pak v dalším průchodu zjednosměrním graf a pak ještě vypíšu všechny zjednosměrněné hrany“. Ve skutečnosti všechno můžu udělat přímo v jednom jediném průchodu grafem, stačí si uvědomit, že algoritmus na hledání mostů nejen že hledá mosty, ale i detekuje dopředné a zpětné hrany, a tak můžeme výsledky ihned vypisovat.
Za funkční řešení v čase O(N+M) bylo možno získat 9 bodů a kdo to všechno zvládl v jednom průchodu grafem, dostal 10 bodů.
17-3-4 Myslitel Cibulka (Zadání)
Myslitel Cibulka by z Vás asi radost neměl. Došlé řešení se totiž dala rozdělit do tří skupin. V první, největší, byla řešení kvadratická. V druhé ta, u nichž autoři ani nenaznačili, proč by měly skončit (a nebylo to, jako u většiny programů zřejmé z toho, že tento cyklus proběhne 3×, jiný N×, …). Ta, ačkoliv byla, jak dále ukážeme, lineární, jsem hodnotil o něco hůř, jelikož byla opravdu triviální, a dokázat o nich, že jsou opravdu rychlá, je mnohem obtížnější, než vymyslet kvadratické řešení. Navíc vymyšlení kvadratického řešení bylo také obtížnější, než vytvoření tohoto triviálního.
No a konečně ve třetí skupině (dá-li se to tak nazvat, skoro by se dalo hovořit o výjimkách potvrzujících pravidlo) byla řešení lineární.
Tak ono „triviální“ řešení. Vezmeme FiBoNaCiHo čísla a sečteme je „po bitech“, tj. po jednotlivých cifrách. Na některých místech se vyskytnou dvojky, kterých se potřebujeme zbavit, a také číslo normalizovat. Jak na to?
Zavedeme kurzor. Budeme předpokládat, že číslo je vpravo od kurzoru normalizované, tj. kdybychom zapomněli (nebo je nastavili na nulu) na všechny cifry nižší, než je pozice kurzoru, tak dostaneme normalizované číslo. A program bude opakovat několik operací, které zřejmě nemění hodnotu čísla a zachovávají výše zmíněný invariant, dokud kurzor nenarazí na konec čísla. Zřejmě když dojde kurzor na „nultou“ cifru (cifry čísla indexujeme od jedničky) tak je celé číslo normalizované a je hotovo.
Pro pohodlnější práci zavedeme ještě nultou a mínus první cifru a zadefinujeme F0=1 a F-1 = 0. Na začátku nastavíme cifry na nula a na konci se jich opět zbavíme. To nám umožní psát pravidlo 2 ·Fn = Fn+1 + Fn-2 pro každé n ≥ 1 (nemám rád okrajové podmínky), a zjednoduší dále některé úvahy.
Teď tělo cyklu. Označme Ci i-tou cifru zpracovávaného čísla a k kurzor (resp. index cifry, na kterou ukazuje).
- Pokud Ck ≥ 1 a Ck+1=1, tak hodnotu cifer k a k+1 snížíme o 1, hodnotu Ck+2 nastavíme na 1 (musela být 0, jelikož číslo vpravo od kurzoru je, jak předpokládáme, normalizované) a kurzor o 2 zvětšíme (mohly se nám vedle sebe dostat dvě jedničky).
- Jinak pokud je Ck ≥ 2 (a Ck+1 = 0, jelikož jinak se provedla předchozí větev), pak Ck+1 nastavíme na 1, Ck-2 zvětšíme o 1, Ck o 2 snížíme a kurzor posuneme o jedna doprava (opět možnost dvojice jedniček).
- A pokud jsme se ještě na nějaké podmínce nezachytili, pak je na pozici kurzoru nula, nebo jednička které nula předchází, a proto se můžeme „beztrestně“ kurzorem posunout o jednu pozici doleva, aniž bychom porušili náš základní invariant.
Až tento cyklus doběhne, musíme se zbavit C0 a C-1. S C-1 není problém, jelikož F-1 je 0 a cokoliv krát nula je stále jen nula, takže tuhle cifru můžeme jednoduše vynulovat. Nyní co s C0. Jak ukážeme později, může nabývat jen hodnot nula a jedna, stačí vyšetřit případ, kdy C0 = 1. Pokud je C1 nula, tak prohodíme nultou a mínus první cifru (protože F0 = F1) a jsme hotovi. Pokud C0 i C1 jsou jedna, tak použijeme pravidlo o dvou jedničkách za sebou a převedeme je na jedničku na druhé cifře. Samozřejmě musíme si dát pozor, jelikož tyto operace mohou narušit normalizaci tím, že se vyskytnou dvě jedničky vedle sebe. Nicméně tato „porucha“ se vyskytuje u čerstvě zapsané jedničky a protože každá redukce dvou jedniček na jednu sníží ciferný součet, zvládneme to vyřešit v lineárním čase.
Je v celku zřejmé, že tělo cyklu nemění hodnotu čísla a že neporuší výše definovaný invariant. Horší je to ale s tím, za jak dlouho tento program doběhne, doběhne-li vůbec. Ještě než se do toho pustíme, dokažme si jedno pomocné tvrzení.
Lemma: Každou cifru, před tím, než se na ní dostaneme kurzorem, můžeme zvýšit nejvýše o jedna. (Pokud považujeme všechny nulové cifry vpravo od čísla za již prošlé)
 Důkaz: Nejdříve takové drobné pozorování.
Označme L nejnižší cifru, na kterou se kurzor při běhu programu zatím dostal.
Potom všechny cifry vpravo od L jsou menší než 2. To se dokáže indukcí. Nejdříve si všimněme,
že jediná operace, která v těle cyklu je schopná zvětšit jedničku na dvojku, je (2),
a ta to dělá vlevo od kurzoru. Pak se podíváme na to, že změnu L je schopná provést jen (3),
a ta to udělá jen tehdy, je-li CL menší než 2. A jelikož vždy platí
k ≥ L, jsme hotovi (alespoň s tímto pozorováním).
Důkaz: Nejdříve takové drobné pozorování.
Označme L nejnižší cifru, na kterou se kurzor při běhu programu zatím dostal.
Potom všechny cifry vpravo od L jsou menší než 2. To se dokáže indukcí. Nejdříve si všimněme,
že jediná operace, která v těle cyklu je schopná zvětšit jedničku na dvojku, je (2),
a ta to dělá vlevo od kurzoru. Pak se podíváme na to, že změnu L je schopná provést jen (3),
a ta to udělá jen tehdy, je-li CL menší než 2. A jelikož vždy platí
k ≥ L, jsme hotovi (alespoň s tímto pozorováním).
Nyní k samotnému lemmatu. Dokážeme ho indukcí dle čísla cifry (označme ho N). Na počátku je k = L rovno délce čísla a pro všechna N ≥ (délka čísla) to zřejmě platí z předpokladů. Nyní předpokládejme, že to platí pro N+1 a větší. Všimněme si opět, že jediná operace, která mění hodnotu cifry vlevo od kurzoru, je (2), a ta to dělá právě o 2 pozice vlevo. Uvažujme L stejné jako v pozorování, na začátku důkazu. Mohou nastat 4 případy:
- L > N+2. Protože tělo cyklu pracuje s ciframi nejvýše o 2 pozice vlevo, tak je tato cifra ještě „nedotčená“ a má svou původní hodnotu.
- L ≤ N. Potom jsme již přes tuto cifru přešli a není co řešit.
- L = N+1. Potom z úvodního pozorování plyne, že CN+2 je menší než 2 a proto se (2) na pozici N+2 již během programu neprovede, a proto se hodnota CN, dokud kurzor nedojde na N, nezmění.
- L = N+2. Z indukčního předpokladu víme, že hodnota CN+2 se zvýšila nejvýše o 1 a proto je menší, nebo rovna 3 (po sečtení bitů je maximálně 2). Pokud provedeme (2), pak hodnota CN+2 klesne na 1 nebo 0. Protože pro všechny cifry vpravo od L platí, že jsou nejvýše 1, a jediná operace, která je schopna zvýšit hodnotu CN+2 nad jedna je (2) a to jen tehdy, je-li kurzor na pozici N+4 (což je vpravo od L), provede se (2) na pozici N+2 nejvýše jednou.
Důsledek 1: Hodnota jakékoliv cifry je během výpočtu nejvýše 3, protože na začátku je nejvýše 2, dokud na ní nedojde kurzor. Zvýšit se může maximálně o 1, ve chvíli, kdy L stojí na této cifře, se tato cifra nemůže zvětšovat (důkaz analogicky jako 4. případ v důkazu lemmatu) a pokud L je vlevo od cifry, pak je tato cifra 1 nebo 0.
Důsledek 2: Hodnota C0 a C-1 je maximálně 1, protože začínaly na nule a kurzor na nich při provádění těla cyklu nemůže stát, tedy zvýší se maximálně na 1.
No a nyní konečně k (ne)konečnosti algoritmu a jeho časové složitosti. Použijeme k tomu techniku, která se nazývá metoda potenciálu. Původně je určená k dokazování konečnosti algoritmu, ale v některých případech ji lze použít i ke stanovení složitosti algoritmu. A co to tedy je?
Odvodíme, uhodneme, nebo jinak stanovíme funkci φ (nějaké parametry, kterými charakterizujeme stav výpočtu (ne nutně jednoznačně)), která je:
- klesající, čili po provedení nějaké části výpočtu, u které je zřejmé, že doběhne za O(cosi) (u konečnosti stačí jen to, že doběhne) se její hodnota ostře sníží.
- klesá „dost“ rychle, to znamená, že existuje konstanta ε>0 taková, že při poklesu v
a)poklesne φ alespoň o ε. (Pozn. je-li funkce φ celočíselná, což v drtivé většině případů je, pak jeb)splněno automaticky.)
Pak pokud ke každým vstupním datům dovedeme shora i zdola omezit
(tj. pro každá vstupní data existují konstanty K a L takové, že
po celou dobu výpočtu platí K≤ φ≤ L), výpočet je konečný.
(ε se „vejde“ do intervalu [K;L] jen konečněkrát). Proto jsme také požadovali „podivnou“ podmínku b).
Vyhnuli jsme se asymptotickému blížení φ ke K a podobným patologickým případům).

 Ale vraťme se k určení složitosti našeho programu.
Označme k pozici kurzoru, σ součet cifer FiBoNaCiHo čísla a
X pozici nejpravějšího výskytu cifry, která je větší než 1
(pokud jsou všechny cifry menší než 2, pak zadefinujeme X = 0). Vezměme tento potenciál: φ(k, σ, X) = k+ 2 X + 3 σ.
Pro parametry zřejmě platí ,že k≥ 0, X ≥ 0 a σ≥ 1 a tedy po celou dobu běhu
programu je φ≥ 3.
Ale vraťme se k určení složitosti našeho programu.
Označme k pozici kurzoru, σ součet cifer FiBoNaCiHo čísla a
X pozici nejpravějšího výskytu cifry, která je větší než 1
(pokud jsou všechny cifry menší než 2, pak zadefinujeme X = 0). Vezměme tento potenciál: φ(k, σ, X) = k+ 2 X + 3 σ.
Pro parametry zřejmě platí ,že k≥ 0, X ≥ 0 a σ≥ 1 a tedy po celou dobu běhu
programu je φ≥ 3.
Na druhou stranu, označme N délku delšího čísla. Na začátku výpočtu zřejmě platí, že X ≤ N a σ≤ 2 N a k= N. Protože, jak ukážeme v dalším odstavci, je φ klesající, platí během výpočtu φ≤ 9 N.
Nyní, co provede s k, X a σ tělo cyklu. Rozebereme jednotlivé větve zvlášť. Čárkované proměnné budou proměnné po provedení těla cyklu, nečárkované před tím.
- Zřejmě nevytváří žádné číslo větší než 2, ale možná nějaké snižuje. Proto X' ≤ X. Ciferný součet se sníží o 1, proto σ' = σ+ 1. A kurzor posuneme o 2 doprava, tedy k' = k + 2. Z toho plyne, že φ' ≤ φ- 1, tedy φ' < φ.
- S ciferným součtem se nic neděje (jen ty dvě jedničky přesuneme na jiné pozice). Protože momentálně pracujeme na nejpravější cifře, která je větší než 1 (viz. pozorování v důkazu lemmatu) a protože každá cifra je během výpočtu nejvýše 3 (viz. důsledek 1), klesá cifra provedením (2) na nejvýše 1 a proto platí X' ≤ X - 1. A kurzor se posune o jedno místo doprava. Proto φ' ≤ φ- 1.
- Poslední případ jen hne s kurzorem a s číslem nic nedělá. Proto φ pro změnu poklesne o 1.
A je to. Uffff…
Poznámka na okraj: ačkoliv je opravdu pozoruhodné, že o tak triviálním řešení se dá dokázat, že běží v lineárním čase, zděšení ze složitosti důkazu není na míste: existují i jiná lineární řešení, která jsou trochu pracnější na naprogramování, ale obejdou se bez složitého dokazování. Například můžeme zkusit přičítat druhé číslo k prvnímu po číslicích a po každé číslici normalizovat. To sice pro některá čísla bude kvadratické, ale stačí si všimnout, že kvadratické chování nastává pouze, objeví-li se blok číslic typu 010101… 01. To můžeme napravit „kompresí“ zpracovávaného čísla – v případě, že za kurzorem následuje takovýto blok, si budeme udržovat pouze jeho délku a ne pokaždé celý blok zkoumat. Hezký algoritmus založený na této myšlence najdete například na http://www.ucw.cz/~mj/papers/fibonacci/.
17-3-5 Jazykozpytcova naděje (Zadání)
Přestože je to úloha na automaty, k jejímu řešení se dalo využít znalosti grafových algoritmů. Automat si představíme jako orientovaný graf, ve kterém je pro každý stav jeden vrchol. Z každého vrcholu vede a orientovaných hran, každá pro jedno písmeno abecedy. Řešení rozdělíme do dvou částí.
Odstranění nedostupných stavů automatu znamená odstranit ty vrcholu grafu, do kterých se nedá dostat z počátečního vrcholu p – vstupního stavu. Projdeme graf do hloubky z počátečního vrcholu a označíme si, kam všude jsme se dostali. Ostatní vrcholy jsou nedostupné. Jediná věc, na kterou si musíme dávat pozor, je, abychom označili každý vrchol pouze jednou.
 Složitějším problémem je nalezení ekvivalentních stavů automatu. Ekvivalentní stavy jsou ty, které stejně
odmítají a přijímají každé slovo. Nechť máme p, q ekvivalentní stavy
a slovo u začínající na x ∈A.
Pak p'=δ(p,x) a q'=δ(q,x) jsou také ekvivalentní. V opačném případě bychom
nalezli slovo v, na které automat ve stavu p' a q' odpoví jinak, a přidali před něj x.
Složitějším problémem je nalezení ekvivalentních stavů automatu. Ekvivalentní stavy jsou ty, které stejně
odmítají a přijímají každé slovo. Nechť máme p, q ekvivalentní stavy
a slovo u začínající na x ∈A.
Pak p'=δ(p,x) a q'=δ(q,x) jsou také ekvivalentní. V opačném případě bychom
nalezli slovo v, na které automat ve stavu p' a q' odpoví jinak, a přidali před něj x.
Vytvoříme si pole velikosti n ·n, do kterého si uložíme, zda jsou stavy i a j ekvivalentní. Pole naplníme hodnotami a pak z něj zkonstruujeme redukovaný automat. Na začátku označíme každý vrchol ekvivalentní sám se sebou a každou dvojici, kde jeden ze stavů je přijímací a druhý nikoli, označíme jako neekvivalentní. Ekvivalenci ostatních dvojic vrcholů budeme zjišťovat rekurzivní funkcí, která pro stavy p a q(parametry) provede:
- Prozatímně je označí jako ekvivalentní.
- Zeptá se pomocí rekurzivního volání, zda jsou ekvivalentní stavy δ(p, x) a δ(q, x) pro každé písmeno v abecedě A.
- Pokud ne, přeznačí stavy jako neekvivalentní.
Teď už můžeme vytvořit redukovaný automat. Místo každé skupiny ekvivalentních stavů vytvoříme jeden stav a tyto stavy pospojujeme.
V algoritmu jsme použili pole, kde jsme uchovávali přechodovou funkci a pole ekvivalencí. Paměťová složitost je tedy O(n2 + n·a). Časově nejnáročnější operací v algoritmu je výpočet ekvivalence. Pro každou dvojici stavů se ekvivalence počítá právě jednou a zahrnuje a dotazů na ekvivalenci dalších stavů. Časová složitost je O(n2·a).