První série sedmnáctého ročníku KSP
Celý leták v PDF.
- Termín série: 18. října 2004
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 17-1-1: Výdělek bratří Součků
- 17-1-2: Bůhdhova odměna
- 17-1-3: Chmatákův lup
- 17-1-4: Paloučkova výhra
- 17-1-5: Jazykozpytcův poklad
17-1-1 Výdělek bratří Součků (10 bodů)
Bratři Součkovi, Ain a Kábel, potomci známého velikého Suka, byli odmala talentovaní hudebníci. Jejich vzájemný vztah bohužel byl, jak jejich jména kážou, dosti špatný. I v dospělém věku si oba konkurovali jako hudební kritici.
Při vzácné příležitosti vystoupení známého zpěváka Miguela J. X. Sona byli oba bratři Součkovi firmou Granny najati, aby se pokusili odposlechnout J. X. Sonův největší hit. Oba bratři – každý sám – koncert navštívili a když se do Sonova hitu zaposlouchali, zjistili, že se neustále opakuje. Tak si oba poznamenali jeho začátek až do chvíle, kdy si byli jisti, že celý hit je jen opakování jimi zaznamenaného začátku.
Při odevzdání svých záznamů ale zjistili, že jsou různě dlouhé! Oba však ale trvají na tom, že zaznamenali skladbu správně, a obviňují toho druhého. Vedoucí firmy Granny, paní Babičková, si však myslí, že ačkoliv jsou jejich zápisy různě dlouhé, mohly by představovat jedinou skladbu. A Vás poprosila, jestli byste jejich zápisy mohli porovnat.
Na vstupu dostanete Ainův i Kábelův záznam. Každý se skládá z délky a pak z jednotlivých not, které budeme pro jednoduchost zapisovat přirozenými čísly. Úkolem Vašeho programu je říci, zda posloupnost, která vznikne jako nekonečné opakování Ainova zápisu je stejná jako ta, která vznikne jako nekonečné opakování zápisu od Kábela.

Příklad: Pokud je Ainův záznam 1,2,1,2,1,2 a Kábelův 1,2,1,2, zaznamenali oba bratři skladbu stejně. Pokud by Ain zaznamenal 1,2,1,2,3,2, nebylo by tomu tak.
17-1-2 Bůhdhova odměna (10 bodů)
Když známý Tigamský kupec Semtodaj Čornulaj Apadaj, věrný reprezentant svého národa, prodal další kus „své“ Tigamské plošiny, rozhodl se Bůhdha, že už se na to nemůže dál koukat. Ovšem jeho hlasité „Budiž černočerná tma!“ se minulo účinkem a vrátilo ozvěnou. (Přeci jenom Bůhdha nemůže být všemocný; kdyby mohl, dokázal by vytvořit neřešitelný problém, který by nevyřešil ani on sám – ale pak by nebyl všemocný. QED.)
A tak si usmyslel, že Tigamany alespoň odmění – obmění jejich jazyky. A to tak, aby si žádní obyvatelé dvou sousedních vesnic nerozuměli. Sousední vesnice jsou takové, mezi kterými vede (samozřejmě horská) pěšina. A protože jsme v horách, žádné dvě pěšiny se nekříží.
Ubohý Bůhdha ale dokázal vymyslet jen 6 odlišných jazyků. Zklamán dosavadními neúspěchy se raději obrátil na Vás, abyste zjistili, zda je možné jeho ďá…božský plán provést.
Máte napsat program, který dostane na vstupu popis Tigamské říše – počet vesnic N a dále M pěšin, každá z nich spojuje právě dvě vesnice. Každá pěšina je obousměrná a navíc platí, že žádně dvě pěšiny se mimo vesnice nekříží (ani nadjezdem, natož tunelem). Úkolem programu je zjistit, zda je možno přiřadit každé vesnici jeden z šesti jazyků tak, aby si žádní obyvatelé sousedních vesnic nerozuměli. Pokud to jde, má vypsat jedno takové přiřazení.
Příklad: Pro následující situaci

stačí Bůhdhovi dokonce jen dva jazyky – rozdá je střídavě.
17-1-3 Chmatákův lup (10 bodů)
 Cecil Hromdotruhlice, Mistr Antibankovních Technologií Álias Kraďas byl zářným potomkem
svého otce. Zdědil po něm vše dobré, co měl a co se tak za nehet vešlo, ale také
všechno špatné. Včetně svého povolání. A ne ledasjakého povolání. Cecil je totiž
profesionální antibankovní činitel – to znamená, že bohatým bere a chudým koneckonců taky.
Sice už nezbyl nikdo,
komu by mohl dávat, než on sám, ale s touto nepříjemností se už všichni Hromdotruhlíkové dávno smířili.
Cecil Hromdotruhlice, Mistr Antibankovních Technologií Álias Kraďas byl zářným potomkem
svého otce. Zdědil po něm vše dobré, co měl a co se tak za nehet vešlo, ale také
všechno špatné. Včetně svého povolání. A ne ledasjakého povolání. Cecil je totiž
profesionální antibankovní činitel – to znamená, že bohatým bere a chudým koneckonců taky.
Sice už nezbyl nikdo,
komu by mohl dávat, než on sám, ale s touto nepříjemností se už všichni Hromdotruhlíkové dávno smířili.
Jednoho dne se Cecil vydal na prohlídku jedné obzvláště bohaté banky v přestrojení za hygienika telefonních sluchátek. Uvnitř ke svému Hromovému překvapení zjistil, že není schopen všechny cenné věci odnést! Chtěl by ale dostát své antibankovní cti a obrat banku o co nejvíc peněz.
Cecil dokáže unést nanejvýš (spíše nanejtíž) N kg lupu. V bance je P cenných věcí a u každé odhadl Cecil její hmotnost na mi celých kg a cenu na ci zlaťáků. Cena, na rozdíl od váhy, může být i desetinné číslo.
Zkuste napsat program, který po zadání popsaných údajů poradí Cecilovi, jaké předměty vzít, aby je ještě unesl a přitom jejich celková cena byla největší možná.
Příklad: Pokud dokáže Cecil unést N=8 kg a v bance jsou
| i | 1 | 2 | 3 | 4 |
| mi | 5 | 4 | 3 | 2 |
| ci | 12.5 | 10 | 6 | 7.5 |
tyto P=4 cennosti, je pro Cecila nejlepší odnést věci 1 a 4. Pokud by ale byla jeho nosnost o kilogram větší (N=9), bylo by nejlepší odnést předměty 2, 3 a 4.
17-1-4 Paloučkova výhra (10 bodů)
Ludvík Palouček, známý to milovník přírody, byl svým přítelem Pepou Běhavým vyzván k běžeckému závodu, který se má odehrát v Běhavého rodném městě. Ludvík se závodu nebojí, protože jeho přítel dostal jméno spíš po svých zažívacích potížích než kvůli rychlým nohám, ale nechce se mu trávit mnoho času jinde než na svém paloučku:„A jak dlouho to bude, Pepo, trvat?“ „Ale, stačí jedno kolečko,“ odpověděl mu vítězství chtivý kamarád.
Ludvík se této odpovědi chytl a rozhodl se naplánovat trasu závodu sám. Závod má začínat a končit na jednom místě (Pepa chtěl kolečko) a přitom má být co nejkratší, aby mohl být Ludvík co nejdřív doma. Když ale uviděl mapu města, zhrozil se a raději Vás požádal o pomoc.
Na vstupu dostanete popis Běhavého města: N, což je počet křižovatek, a dále M ulic. Každá ulice je obousměrná, má nějakou délku a spojuje dvě křižovatky. Ačkoliv se ulice mimo křižovatky nekříží, ve městě může být mnoho nadjezdů a tunelů.
Vaším úkolem je zjistit, zda ve městě existuje nějaký okruh, a pokud ano, máte najít a vypsat libovolný nejkratší z nich i s jeho délkou. Okruh je posloupnost alespoň dvou neopakujících se ulic, přičemž po sobě následující ulice okruhu začínají a končí na stejné křižovatce – včetně první a poslední ulice okruhu. Délkou okruhu rozumíme součet délek všech jeho ulic.
Příklad: Pokud je v městě N=5 křižovatek a ulice
| odkud | kam | délka |
| 1 | 2 | 2 |
| 2 | 3 | 3 |
| 1 | 3 | 9 |
| 3 | 4 | 1 |
| 4 | 5 | 3 |
| 1 | 5 | 2 |
tak nejkratší je okruh 1→2→3→4→5→1 délky 11. Všimněte si, že 1→2→1 není okruh, protože je skládá z jediné opakující se ulice (a to se nesmí).
17-1-5 Jazykozpytcův poklad (10 bodů)
Co mají společného překladače programovacích jazyků, vyhledávání v textu, komprese dat nebo třeba také rozdělování slov? Na první pohled nepříliš, ale teoretickým informatikům se přesto podařilo najít teorii, která shrnuje základní věci z těchto oblastí (a mnohých jiných) a říká o nich mnoho zajímavého. Je to teorie automatů a formálních jazyků a právě té jsme se rozhodli věnovat náš letošní seriál.
Začneme nejprve názvoslovím:
- Abeceda je libovolná konečná množina znaků.
- Slovo α nad abecedou A je uspořádaná konečná posloupnost znaků abecedy A. Prázdné slovo značíme λ. Množinu všech možných slov nad abecedou A značíme A*.
- Jazyk L nad abecedou A je nějaká podmnožina (klidně nekonečná) množiny A*. Nenechte se zmást názvem jazyk, nemáme tím na mysli nějaký specifický programovací či dokonce přirozený jazyk (i když i tyto do naší definice spadají), jedná se zkrátka o nějakou množinu slov.
- Jsou-li α a β dvě slova, pak zápisem αβ rozumíme jejich zřetězení za sebe.
- Zápisem αi rozumíme i-násobné opakování slova α (tj. třeba (ab)2=abab).
Příklad: nad abecedou {a,b,c} lze vybudovat třeba jazyky {baba, abba, bac} (ten je konečný) či {aibi; ∀i∈N} (ten je nekonečný a patří do něj třeba slova ab či aaabbb, nepatří tam abb ani bbbaaa).
U každého jazyka lze studovat například tyto dvě věci: jak daný jazyk rozpoznávat (rozhodnout o zadaném slovu, zda patří do jazyka) a jak generovat všechna slova daného jazyka. K prvnímu úkolu slouží „stroje“ čili automaty, s jejichž nejběžnějšími typy se v seriálu seznámíme. To druhé mají na starost gramatiky. Gramatika je formální popis pravidel, pomoci kterých se vytvářejí všechna slova daného jazyka. Původně je vymyslel lingvista pan Chomsky pro popis přirozených jazyků – z hodin českého jazyka jistě znáte větné rozbory, tj. pravidla typu [věta] → [podmětná část][přísudková část], kde podmětná a přísudková část se opět rozpadají na podčásti, atd. Gramatika se tedy skládá ze sady přepisovacích pravidel α→β, kde na obou stranách vystupují slova sestávající se jednak z pomocných symbolů (těm se říká neterminální) a jednak ze symbolů terminálních (po domácku terminálů), které už se dále neexpandují (čili už se na ně dále nepoužívají přepisovací pravidla). Terminály se vlastně dají chápat jako jednotlivé znaky použité abecedy.
Formální definice je následující: Gramatikou nazveme čtveřici (VN,VT,S,P), kde:
- VN je konečná množina neterminálních symbolů,
- VT je konečná množina terminálních symbolů,
- S∈VN je počáteční neterminální symbol,
- P je konečný systém přepisovacích pravidel α→β, kde α,β∈(VN∪VT)* a α obsahuje alespoň jeden neterminální symbol. Dvě pravidla α→β a α→γ obvykle zkráceně zapisujeme jako α→β| γ.
Gramatika vezme počáteční symbol a začne ho expandovat (nahrazovat) podle některého z uvedených pravidel. Typicky bývá několik možností, jak expandovat, tehdy můžeme použít libovolné vhodné pravidlo. Expanze končí, když z expandovaného řetězce vymizí všechny neterminální symboly. Všechna možná slova, která pomocí jedné gramatiky G můžeme různými posloupnostmi expanzí dostat, tvoří jazyk gramatiky, ten budeme značit L(G).
Jako příklad si uvedeme gramatiku, která popisuje jazyk všech aritmetických výrazů s čísly 1 a 2 používajících operace + a * a závorky. Použijeme neterminální symboly VN={V,T,F}, terminální symboly VT={1,2,+,*,(,)}, počáteční symbol je V a pravidla:
| V | →T+V | T |
| T | →F*T | F |
| F | →(V) | 1 | 2. |
Například výraz 1+2*2 je generován posloupností přepisů V→T+V→F+V→1+V→1+T→1+F*T→1+F*F→1+2*F→1+2*2. Slovo 22++1 zjevně pomocí sady našich pravidel nevytvoříme.
V prvním dílu seriálu se seznámíme s nejjednodušší rodinou jazyků – regulárními jazyky. Regulární jazyk je takový jazyk, ke kterému existuje konečný automat, který ho rozpoznává.
Co že to ten konečný automat (též zkratkou KA) vlastně je? Matematici mají rádi nejrůznější uspořádané k-tice, formálně si proto konečný automat zavedeme jako pětici (Q, A, δ, q0, F), kde:
- Q je konečná množina stavů stroje,
- A abeceda, nad kterou stroj pracuje,
- δ: Q×A→Q je tzv. přechodová funkce, která ke každé kombinaci stavu a načteného znaku určuje nový stav, do kterého automat přejde,
- q0∈Q je počáteční stav,
- F⊆ Q je množina koncových (přijímajících) stavů.
A nyní lidsky: konečný automat je stroj, který dostane na vstupu nějaké slovo a má se o něm rozhodnout, zda ho přijme či nikoliv. Automat se může nacházet v konečné a předem dané množině stavů Q, na začátku dejme tomu ve stavu q0. V každém kroku své činnosti načte jeden znak ze vstupu a podle tohoto znaku se rozhodne, do jakého stavu přejde. To je dáno přechodovou funkcí, která k aktuálnímu stavu q a znaku a vrátí nový stav q', tedy δ(q,a)=q'. Pokud po přečtení všech znaků slova automat skončil v některém z přijímacích stavů z množiny F, říkáme, že slovo bylo přijato, jinak bylo odmítnuto. Všechna slova, která daný automat A přijímá, tzv. jazyk automatu, značíme L(A).
Příklad: automat nad abecedou {a,b}, přijímající všechna slova s právě třemi výskyty znaku a a libovolným počtem výskytů znaku b. Automaty je nejpřehlednější zapisovat obrázkem:
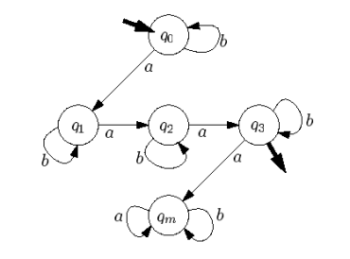
Automat má 5 stavů, stav q0 je počáteční, stav q3 je jediný přijímací. Stav qi nám vlastně značí, že doposud jsme načetli i znaků a, stav qm je záchytný a znamená, že a-ček už jsme přečetli moc.
| * |
| T |
Ale nyní již
Soutěžní úlohy:
1. Uvažme abecedu A={0,1}. Slovo nad touto abecedou bude kódovat číslo zapsané v dvojkové soustavě, s obvyklou konvencí, tj. nejvýznamnější bit nalevo, nejméně významný napravo. Sestrojte konečný automat nad A rozpoznávající všechna čísla dělitelná třemi a nedělitelná dvojkou (tj. jeho jazykem budou všechna slova kódující číslo dělitelné 3 a nedělitelné 2). [5 bodů]
2. Sestrojte gramatiku se stejným jazykem jako v první úloze – tj. generující právě čísla v binárním zápisu, která jsou dělitelná třemi a nejsou dělitelná dvojkou. [5 bodů]
Kromě zkonstruovaného automatu a gramatiky by měl být součástí řešení i stručný slovní popis toho, proč daný automat resp. gramatika dělá to co má, případně důkaz, že hledáme marně a to, co chceme, neexistuje.