Druhá série sedmnáctého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 13. prosince 2004
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 17-2-1: Prasátko Květ(ák)omil
- 17-2-2: Bobr Béďa
- 17-2-3: Krkavec Kryšpín
- 17-2-4: Mravenec Ferda
- 17-2-5: Jazykozpytcova pomsta
Milí řešitelé!

Je tady podzim a s ním druhá série našeho semináře. Tentokrát Vám přišla bez opravené první série. Nicméně dříve, něž budete muset tuto druhou sérii odevzdat, dostanete spolu se zadáním třetí série i Vaše opravená řešení série první. Prostě podzim :–)
Pokud chcete posílat svá řešení elektronickou cestou, prosím držte se instrukcí, které můžete najít na http://ksp.mff.cuni.cz/submit/. Řešení, která přišla mailem, jsme přijali pouze výjimečně.
17-2-1 Prasátko Květ(ák)omil (10 bodů)
Květomil byl úplně normální prasátko. Již v útlém dětství ničím nevynikal mezi svými vrstevníky, své rodiče nepřekvapoval svou předčasnou duševní vyspělostí. Ani později nijak nezastiňoval své přátele a známé v žádné činnosti, kterou prováděl, snad s jedinou výjimkou, a tou bylo jídlo (proto si vysloužil přezdívku Pašík Kvašík). Byl prostě úplně normální obyčejné prasátko.
Když vyrostl, zvolil si úplně normální obyčejné povolání a stal se programátorem u firmy Ptáček Sáček, práce všeho druhu. Jeho práce u této firmy (konkurující známému příteli Ferdy Mravence) byla také úplně normální a obyčejná. Proto, když Sáček kontroloval práci svých zaměstnanců, aby zjistil, proč jeho konkurence dodává rychlejší programy, zjistil, že programy Pašíka Kvašíka jsou pomalé až hrůza. Prostě úplně normální a obyčejné.
A tak si Sáček najal Vás, abyste mu pomohli Kvašíkovy programy zrychlit. Kvašíkovy programy jsou posloupnosti přiřazení do proměnných, což jsou řetězce znaků složené z malých písmen, velkých písmen a podtržítek. Na pravé straně přiřazení může být buď proměnná nebo operace „+“ nebo „*“ aplikovaná na dvě proměnné. Tyto operace jsou komutativní, neboli a+b=b+a a a*b=b*a.
Vaším úkolem je napsat program, který dostane Kvašíkův program skládající se z N přiřazení a má říci, jak moc ho lze zrychlit, čili říci, kolik nejméně operací „+“ a „*“ stačí k tomu, aby nový program přiřadil do všech proměnných stejnou hodnotu jako Kvašíkův. Formálně pro každých i prvních řádků Kvašíkova programu musí v novém programu existovat místo, kdy jsou hodnoty všech proměnných z Kvašíkova programu v obou programech shodné. Můžete využívat toho, že operace „+“ a „*“ jsou komutativní, ale jejich asociativita a distributivita se neberou v úvahu, čili a+(b+c)≠ (a+b)+c a také (a+b)*c≠ a*c + b*c.
Příklad: Vlevo je Kvašíkův program, vpravo náš.
t = b + c;
a = b + c; a = t;
d = a + b; d = a + b;
e = c + b; e = t;
s = a * e;
f = a * e; f = s;
a = d; a = d;
g = e * e; g = s;
Zatímco Kvašíkův program potřeboval operací pět, náš si vystačí se třemi, takže výstup programu by měl být „3“.
17-2-2 Bobr Béďa (10 bodů)
Béďa byl hodný bobr, který poslouchal svou maminku. A ta ho, jako každá jiná maminka, naučila čistit si zoubky. Když Béďa vyrostl, začal používat zubní pastu Bělosup, po které, jak bylo na jejím obalu napsáno, „zuby nádherně vypadají.“
A byla to pravda. Hodnému Béďovi vypadaly všechny zuby. Dostal sice samozřejmě umělé, ale protože bobři vyrábějí vše ze dřeva, byly celé dřevěné. Leč s dřevěnými zuby Béďa nemohl chodit do normální bobří práce, protože by sotva přehryzal dřevěný strom. A tak začal pracovat u firmy Ptáčka Sáčka.
Přestože byly Béďovy zuby dřevěné, stále dokázal skvěle pracovat se dřevem, a tak byl zaměstnán jako výrobce integrovaných odvodů. Integrovaný odvod je součástka na rozvod vody. Představit si ji můžete jako dřevěnou desku, na které je pravidelná čtvercová síť bodů, některé sousední body jsou spojeny vydlabanou spojnicí. Za sousední body se považují takové, které se liší v jedné souřadnici o jedničku (čili vnitřní body mají každý čtyři sousedy). Béďův úkol je dodělat na odvod nějaké spojnice sousedních bodů, aby bylo možné dostat se z každého bodu do jiného.
Protože je integrovaný odvod ze dřeva, dokáže Béďa vytvořit svislé spojnice rychleji než vodorovné (jdou „po letech“). Změřil si, že udělat jednu vodorovnou nebo dvě svislé spojnice mu zabere stejně času. A protože je Béďa hodný, chce mít každý odvod co nejrychleji hotový.
Napište Béďovi program, který dostane na vstupu N a M (rozměry mřížky bodů na integrovaném odvodu), S (počet již hotových spojnic), a popis jednotlivých spojnic (souřadnice dvou bodů, které spojuje). Výstupem by měl být seznam spojnic takových, že po jejich přidání do integrovaného odvodu se půjde dostat z každého bodu do každého a navíc doba na vytvoření těchto spojnic bude co nejmenší (čili neexistuje jiná množina spojnic, která by se dala vyrobit v kratším čase a přitom by splnila popsanou podmínku).
Příklad: Pro N=4,M=4 a odvod

je pro Béďu nejlepší vytvořit spojnice nakreslené dvojitě.
17-2-3 Krkavec Kryšpín (8 bodů)
Krkavec Kryšpín byl velmi známý a uznávaný básník, snad každý se obdivoval jeho poezii. Což ale znamená, že to byl básník velmi zaneprázdněný, protože každé zvířátko po něm chtělo jinou básničku. Jako každý básník i Kryšpín potřeboval inspiraci – zpěv ptáků. Ovšem po čase se mu všichni ptáci začali vyhýbat, nebavilo je věčně stát před krkavcem, který je neustále napomínal, ať nekrákají.
To se Kryšpínovi ani trochu nelíbilo a usmyslel si, že zpěvavé ptáky nějak naláká. Rozhodl se, že jim postaví fontánu roztodivného tvaru – ptáci budou obdivovat fontánu (hned ji překřtil na Fontárnu, když u ní bude psát básně), on ptačí zpěv a ostatní jeho poezii.
Hned vyrobil zkušební Fontárničku, ale zjistil, že potřebuje najít její těžiště, aby mu nepadala ze stojánku. Vypravil se za Ptáčkem Sáčkem, zda by mu jeho firma mohla pomoci, ale Sáček se mu jenom vysmál, protože nechtěl zradit své ptačí přátele. Dokážete Kryšpínovi poradit Vy?
Na vstupu dostanete N bodů zadaných svými souřadnicemi, které představují Fontárnu. Tu si můžete představit jako mnohoúhelník, který vznikne, spojíme-li vždy dva po sobě jdoucí zadané body (a ještě první s posledním). Tento mnohoúhelník je navíc konvexní, což znamená, že všechny jeho vnitřní úhly jsou menší než 180°. Vaším úkolem je najít těžiště zadaného mnohoúhelníka.
Příklad: Pro N=4 a body [0,0],[12,6],[12,12],[0,18] by měl Váš program odpovědět, že těžiště se nachází na souřadnicích [5,9].
Pro náročnější: Pokud bude Váš program fungovat i pro nekonvexní mnohoúhelníky, můžete dostat další 3 body.
17-2-4 Mravenec Ferda (11 bodů)

Ferdova tajná láska, Beruška, přišla jednou za ním a jeho přítelem Pytlíkem na návštěvu. K Ferdově veliké lítosti ale odmítla jeho návrh najít stonožku Šmajdulu a svázat jí nohy dohromady, a místo toho se podivovala Pytlíkově kvetoucí firmě. Zklamaný Ferda se rozhodl Berušce předvést, že co dokáže jeho přítel, dokáže taky. Aby ale nemusel začínat s prázdnými tykadly, rozhodl se, že se stane vedoucím firmy Ptáček Sáček, práce všeho druhu.
Příští den zašel do Sáčkovy firmy a spustil: „Podívejte se na něj, na ptáčka. Zaměstnává naprosto neschopné programátory, chudáčkovi Bobrovi vyrazil zuby, aby pro něj vyráběl odvody a je to takový trumbera, že ani nedokáže spočítat těžiště. A takové zvíře Vám má šéfovat?“ Zvířátka uznala, že na tom je něco pravdy, a rozhodla se dát Ferdovi šanci. Když vyřeší jejich úlohu, stane se jejich šéfem.
Zvířátka položila před Ferdu N kostiček domina, na každém jsou nahoře a dole dvě celá čísla od 1 do K. Každou kostičku domina může Ferda obrátit, čili její horní číslo se dostane dolů a naopak. Jeho úkolem je dosáhnout toho, aby rozdíl součtu horní a dolní řady čísel na kostičkách byl co nejmenší. A navíc toho má dosáhnout přehozením co nejmenšího počtu kostiček. Ferda ale zjistil, že je to i nad jeho mravenčí síly. Pomůžete mu?
Příklad: Pro K=8 a N=6 a dominové kostky
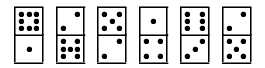
musí Ferda otočit druhou, třetí a pátou dominovou kostku.
Pozor: I sám Ferda si po chvíli přemýšlení uvědomil, že nestačí najít si kostičku s největším rozdílem čísel, která by mu pomohla snížit celkový rozdíl, otočit ji, a podle stejného postupu pokračovat dál (to nezabere ani pro uvedený příklad). Kdyby to bylo takhle jednoduché, určitě by Vás o pomoc nepožádal.
17-2-5 Jazykozpytcova pomsta (10 bodů)
V druhém dílu seriálu o formálních jazycích se ještě stále budeme věnovat nejjednodušší jazykové rodině, regulárním jazykům. Minule jsme si řekli, co jsou to gramatiky, konečné automaty a regulární jazyky, a nyní si zavedeme věc, která se může na první pohled jevit jako naprostý nesmysl – nedeterminismus. Pokud pracuje nějaký proces (stroj, algoritmus, …) deterministicky, pak pokud známe jeho vstupní data, jsme schopni dopředu předpovědět, jak se bude chovat. Ovšem u nedeterministického procesu nic takového určit nemůžeme.
Pokud je konečný automat ve stavu q a načte nové písmeno p, je pomocí přechodové funkce přesně definováno, jaký bude nový stav, do kterého stroj přejde. Ovšem nedeterministický konečný automat má k jedné kombinaci stavu a písmena na výběr hned několik možných stavů, do kterých může přejít, a z těch si jeden naprosto libovolně vybere.
Formálně je nedeterministický konečný automat (NKA) pětice (Q,A,S, δ, F), kde
- Q je konečná množina stavů,
- A je konečná abeceda, nad kterou automat pracuje,
- S je množina počátečních stavů,
- δ: Q×A →P(Q) je přechodová funkce, která ke každé kombinaci aktuálního stavu a nově načteného písmenka vrací neprázdnou množinu stavů (tedy nějakou podmnožinu Q), do kterých automat může přejít,
- F⊆ Q je množina přijímacích stavů.
Zbývá nadefinovat, kdy je či není dané slovo nedeterministickým konečným automatem přijato. Výpočtem NKA nad slovem w rozumíme konkrétní průběh činnosti stroje při postupném čtení písmen slova w. Díky nedeterminismu je možných výpočtů pro jediné slovo více. Slovo w je tedy přijato, jestliže mezi všemi možnými výpočty nad slovem w existuje alespoň jediný, který končí v přijímacím stavu.
Příklad NKA nad abecedou A={a,b}:
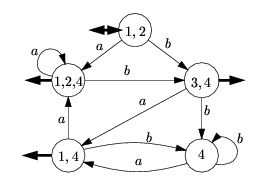
Stroj používá stavy Q={1,2,3,4}, počáteční stavy jsou S={1,2} a koncové F={1,3}. Ve stavech 1 a 4 jsou dvě možnosti, jak se při načtení písmena a může stroj zachovat.
Ačkoli to tak na první pohled rozhodně nevypadá, přidáním nedeterminismu do konečných automatů jsme ve skutečnosti nijak nezvedli „výpočetní sílu“ stroje.
Tvrzení.
Množina jazyků přijímaných deterministickými KA je
stejná jako množina jazyků přijímaných nedeterministickými KA.
Jinými slovy, ke každému NKA jsme schopni sestrojit ekvivalentní (přijímající stejný jazyk) DKA a naopak. Tato skutečnost rozhodně stojí za to být dokázána. První převod je jednoduchý, každý DKA je totiž pouze případem takového NKA, jehož přechodová funkce vrací vždy jednoprvkovou množinu stavů. Převod druhý je však už o poznání těžší.
Mějme libovolný nedeterministický konečný automat M=(Q,A,S,δ,F) a hledejme k němu ekvivalentní deterministický konečný automat M'=(Q',A,q'0,δ',F'). Nejprve se zamysleme, jak bychom asi M simulovali „programátorsky“. Nejspíše bychom si napsali program, který pro vstupní slovo probacktrackuje všechny možné výpočty. Další metodou je v každé situaci, kdy se M rozhoduje z několika možností, spustit pro každou takovou možnost paralelně proces, který ji dále simuluje. Právě na této myšlence je založena naše konstrukce. Jak ovšem takový postup namodelovat omezenými prostředky konečných automatů?
V novém konečném automatu M' především podstatně rozšíříme množinu stavů, položíme Q'=P(Q), kde P(Q) značí množinu všech podmnožin množiny stavů Q původního stroje M. Jeden stav stroje M' tedy bude kódován hned několika stavy stroje M. Počáteční stav bude q'0=S, čili množina obsahující všechny počáteční stavy stroje M. Přechodovou funkci δ'(q',a) pro q'={q1,q2,…,qk}∈Q' a a∈A definujeme takto:
Všimněte si, že v jednom stavu z Q' jsme schopni najednou simulovat hned několik stavů původního stroje. Stejně tak nová přechodová funkce δ' provede paralelní výpočet hned pro několik stavů původního stroje najednou. Zbývá položit F'={q'∈Q'; ∃q∈q': q∈F}, čili přijímací stav stroje M' je taková množina stavů stroje M, ve které se vyskytuje alespoň jeden přijímací stav stroje M.
Právě jsme si ale uvědomili, že v jednom stavu z Q' paralelně simulujeme několik různých výpočtů původního stroje. Podle definice přijímání nedeterministickým konečným automatem je přijímací stav z F' takový, že alespoň jeden výpočet z odpovídající množiny výpočtů stroje M je přijímací. Oba stroje tedy přijímají stejný jazyk, čímž je důkaz hotov. Počet stavů nového stroje M' nám sice oproti M exponenciálně narostl, ale je stále konečný a splňuje tak definici konečného automatu.
Nás ukázkový stroj tedy po převodu bude vypadat takto (nikdy nedosažitelné stavy z obrázku vynecháme):
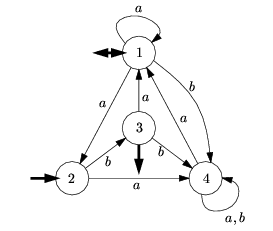
Zavedením nedeterminismu jsme tedy nijak nerozšířili možnosti konečných automatů, nicméně právě předvedená věta se dá třebas využít k zjednodušení nejrůznějších důkazů. O strojích, jejichž nedeterministická verze má větší výpočetní sílu než verze deterministická, si povíme v příštích dílech seriálu.
Ale nyní už asi netrpělivě čekáte na další
Soutěžní úlohy:
- Každý stroj má svá omezení a nejinak tomu je v i případě konečného automatu.
Nechť U je jazyk nad dvoupísmennou abecedou {(,)}, který je tvořen všemi
správně uzávorkovanými výrazy. Např. slovo ()(()) patří do U, slovo ))( do U nepatří.
Pokud možno formálně dokažte, že nemůže existovat konečný automat,
který by rozpoznával jazyk U.
[6 bodů]
- Nechť L1 a L2 jsou libovolné regulární jazyky.
Zřetězením regulárních jazyků L1 a L2 nazveme jazyk
L1.L2={uv; u∈L1, v∈L2}.
Tedy např. pro L1={a,ab} a L2={ci; i∈N}
je L1.L2={ac,abc,acc,abcc,…}.
Dokažte, že L1.L2 je také regulární jazyk.
[5 bodů]
Připomínáme, že vaše řešení by měla obsahovat matematicky správné zdůvodnění a nikoli zdrojový kód programu počítajícího bůhvíco.