Čtvrtá série sedmnáctého ročníku KSP
Celý leták v PDF.
- Termín série: 21. březen 2005
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 17-4-1: Mandarinková zeď
- 17-4-2: Válicie
- 17-4-3: Phirma
- 17-4-4: Antifrňákovník
- 17-4-5: Jazykozpytec vrací úder
Milí řešitelé!

Vánoce jsou definitivně za námi. Stromeček dohořel, cukroví dojedli holubi a kapr zase přežil. Tak si oblékněte ten hnědý pletený svetr a ty vlněné ponožky, co jste našli pod stromečkem, a podívejte se, co vám ještě Ježíšek nadělil. Nemusíte pospíchat, protože na tuhle sérii máte skoro stejné množství času jako na přípravu pomlázky a barvení velikonočních vajíček.
17-4-1 Mandarinková zeď (10 bodů)
Veliký císař Čching Ňamňam No-san byl osvíceným vládcem Mandarínie. A jako osvícený vládce znal i zvyky a svátky jiných zemí. Ze všeho nejvíce se mu líbil jakýsi křesťanský svátek – Vánoce. Ten den totiž všichni dostávají mnoho dárků a on jako veliký osvícený panovník by jich určitě dostal opravdu mnoho. A tak se rozhodl, že se v Mandarínii budou Vánoce slavit také.
Prostí Mandaríni a Mandarínky nebyli ovšem jeho nápadem moc nadšeni, protože hlavní postava Vánoc Santa Hood-san měl podle No-sana chudým brát a jemu dávat. A proto se císař rozhodl, že si raději zkontroluje, jestli budou jeho poddaní Vánoce radostně slavit.
Kolem celé Mandarínie je postavena Velká Mandarinková zeď. Na této zdi jsou v pravidelných rozestupech strážní věže a v každé je jeden strážce. A No-san chce, aby právě tito strážci kontrolovali dodržování Vánoc. Práce strážců je ovšem velmi nudná, a tak každý strážce požaduje jistý počet různých medailí, aby byl se svou prací spokojen.
Císař chce všem strážcům vyhovět, ovšem rád by ušetřil, a tak se rozhodl použít co nejméně druhů medailí a rozdat je strážcům tak, aby každý dostal právě tolik různých medailí, o kolik si řekl, a navíc žádní dva sousední strážci neměli medaili stejného druhu (to, že nějaký strážce vidí, že jeho levý a pravý soused mají stejné druhy medailí, už císařovi nevadí). Poradíte?
Na vstupu dostanete počet strážních věží N a dále čísla a1 až aN, kde ai reprezentuje počet medailí vyžadovaných strážcem číslo i. Vaším úkolem je zjistit, kolik nejméně druhů medailí je potřeba, aby každý strážce dostal, kolik chce různých druhů medailí, a aby žádní dva sousední strážci (sousedí spolu strážci i a (i+1) a navíc ještě N a 1) nedostali ani jednu medaili stejného druhu.

Příklad: Pro 5 strážců a požadavky 2,2,2,2,2 je minimální počet medailí 5.
17-4-2 Válicie (10 bodů)
Poté, co byl Santa Hood-san několikrát, zrovna když se jako na potvoru nedíval žádný strážce, zboulován, rozhodl se No-san, že bude muset prosazovat Vánoce ještě o něco důrazněji. A tak se rozhodl zavést v Mandarínii Vánoční policii, zvanou Válicie. (I když zlí jazykové tvrdí, že její název pochází spíš od toho, že si Válicisti stále válí šunky.)
Mandarínie je vlastně jedno velké město (obehnané zdí). A aby v něm císař udržel pořádek, rozhodl se postavit na některých křižovatkách stanice Válicie, a to tak, aby na konci každé ulice byla alespoň jedna stanice. Ale aby se nestalo, že na sebe v temných a strašidelných uličkách Mandarínie zaútočí Válicisté ze dvou stanic, které jsou na koncích jedné ulice, je třeba postavit stanice tak, aby na koncích každé ulice ve městě byla postavena právě jedna stanice. Císař je (jako obvykle) velký škudlil a minimalista, a tak by chtěl, aby stanic musel postavil co nejméně.
Na vstupu dostanete graf o N křižovatkách a M ulicích. Každá ulice je obousměrná a spojuje právě dvě křižovatky a žádné dvě ulice se mimo křižovatky nekříží (mimoúrovňově mohou). Vaším úkolem je zjistit, na kolika nejméně křižovatkách je třeba postavit Válicejní stanice tak, aby na koncích jedné ulice byla stanice právě jedna. Kromě počtu těchto křižovatek vypište i křižovatky, kde mají stanice stát. Pokud je řešení více, stačí vypsat libovolné řešení, pokud není řešení žádné, vypište odpovídající zprávu.
Příklad: Pro 6 křižovatek a 4 ulice spojující křižovatky (1,2), (1,5), (3,4) a (1,6) jsou potřeba dvě stanice na křižovatkách 1 a 3. Pro 3 křižovatky a 3 ulice (1,2), (2,3) a (3,1) stanice postavit nejde.
17-4-3 Phirma (10 bodů)
Poté, co dokázal No-san udržet v Mandarínii klid, se jeho pozornost přesunula k tomu, aby, když už Vánoce tak horko těžko zavedl, dostal odpovídající množství dárků. A protože mezi chudými už mnoho dárků hodných Velkého No-sana nebylo, rozhodl se je hledat jinde.
Snad nejznámější firmu v Mandarínii založili paní Čestná a pan Jakobi. A protože firma dělala čest svému jménu, byla také nejbohatší. Ledva to císař zvěděl, rozhodl, že mu Vánoční dárek zaplatí právě ona.
Firma Jakobi-Čestná musí dodat časově seřazený seznam výdajů a příjmů a císař určí daně podle toho, jak dlouhé bylo nejdelší časové období, kdy firma vykazovala zisk (takzvaný kradit). Ovšem účetní této firmy dokážou falšovat zisky opravdu bleskově, proto by No-san potřeboval zjistit požadované údaje co nejrychleji. A tak se obrátil na Vás.
Napište císaři program, který dostane na vstupu číslo N a dále posloupnost N celých čísel. Vaším úkolem je najít a vypsat nejdelší úsek (to je souvislá podposloupnost) takový, že součet čísel v tomto úseku je větší než nula. Pokud je takových úseků více, vypište libovolný s největším součtem.
Příklad: Pro posloupnost (1,-2,-5,1,1,1,1,1,1,-1) má hledaný nejdelší úsek délku 7 a je to úsek (1,1,1,1,1,1,-1).
17-4-4 Antifrňákovník (10 bodů)
Mandarínům se nakonec No-sanovy klidné Vánoční svátky natolik znelíbily, že se rozhodli císaři utéct. Ovšem Mandarinková zeď obsazená strážemi s jejich záměry moc nesouhlasila. A tak si Mandaríni, aby se na útěk mohli pořádně připravit, založili Sportovní Klub Utek' & Utekl.
Po dlouhé debatě se členové SK Utek' & Utekl dohodli, že si postaví stroj antifrňákovník, který Mandarinkovou zeď rozbije, a oni budou moci utéct. Ale aby jejich práce nemohla být No-sanovi nikým z nich prozrazena, rozhodli se, že každý bude znát pouze část antifrňákovníku.
Jaké bylo nakonec jejich (ale ne naše) překvapení, když po sestavení celého přístroje zjistili, že nikdo neví, jak propojit jeho elektrické obvody. Dokonce ani neví, jaké konce drátů na jednom konci přístroje odpovídají koncům na straně druhé. A protože si No-san usmyslel, že právě Vy budete dalším sponzorem jeho Vánočních dárků, rozhodli jste se s dokončením antifrňákovníku pomoci.
Na obou koncích přístroje je N konců drátů očíslovaných 1 až N a dále zemnění, což je drát, o kterém jako jediném víte, jak je propojen. Můžete vlevo dráty na zemnění napojovat a odpojovat a na pravé straně můžete měřit, zda mezi koncem drátu a zemněním teče elektrický proud. Vaším úkolem je říci, jaký konec drátu na straně levé je spojen s jakým koncem na straně pravé. Bohužel se může stát i to, že některé dráty jsou přerušeny a nevedou nikam.
Máte tedy napsat program, který dostane na vstupu počet konců drátu N,
vypisuje příkazy +X pro připojení levého konce X-tého drátu na zemnění,
-X pro odpojení levého konce X-tého drátu od zemnění a ?X pro
změření napětí na pravém konci X-tého drátu a zemnění (na tyto dotazy
odpovídá uživatel). Nakonec má vypsat, které levé konce drátů jsou připojeny
na jaké pravé (nevodivé dráty nevypisujte vůbec, vodivé vypište všechny). S levým i pravým koncem drátu může být spojen
nanejvýš jeden opačný konec. Na začátku není na zemnění
připojen žádný konec levého drátu.
Příklad: Pro N=3 a následující „rozhovor“
| výstup programu | uživatelský vstup |
| +1 | |
| ?1 | Ano |
| -1 | |
| +2 | |
| ?3 | Ano |
| -2 | |
| +3 | |
| ?2 | Ne |
je správná odpověď 1→1, 2→3.
17-4-5 Jazykozpytec vrací úder (15 bodů)
Minule jsme si praktičtější úlohou odpočinuli od rozmanité teorie formálních jazyků, což nyní opět napravíme. Nastal čas, abychom od jednoduchých regulárních jazyků pokročili k složitějším bezkontextovým jazykům. Název těchto jazyků plyne ze souvislosti s gramatikami, jíž si ovšem ukážeme až v příštím díle seriálu. (Nezasvěceným doporučujeme, aby si prostudovali seriálové úlohy předchozích sérií.)
Zavedeme si podstatně mocnější výpočetní prostředek než byl konečný automat, tzv. zásobníkový automat. Ten vznikne tak, že starý známý konečný automat vybavíme zásobníkem, což je paměť potenciálně neomezené kapacity, ve které jsou naskládané symboly z nějaké pevné abecedy, ale je možno přistupovat vždy jen k symbolu, který je na vrcholu a buďto tento symbol odebrat a nebo přidat další nad něj.
Většina vlastností KA zůstane zachována, jen přechodová funkce se nyní bude počítat z kombinace aktuálního stavu, písmene na vstupu a symbolu na vrcholu zásobníku, tedy trojice (q, p, z). Funkce potom vrátí nový stav, do kterého má stroj přejít, a také posloupnost symbolů, kterými se nahradí dosavadní vrchol zásobníku. Oproti konečnému automatu, který v každém kroku musel ze vstupu přečíst právě jedno písmeno a z něj počítat přechodovou funkci, umí zásobníkový automat také načtení písmene vynechat, což si můžeme představovat jako načtení prázdného znaku λ (a přechodovou funkci tudíž počítat z trojice (q,λ,z)). Vše si zavedeme formálně.
Deterministický zásobníkový automat (DZA) M je sedmice
kde
- Q je konečná množina stavů,
- A je konečná vstupní abeceda,
- Z je konečná zásobníková abeceda (tedy symboly, které lze ukládat na zásobník),
- δ: Q×(A∪{λ})×Z →Q×Z* je přechodová funkce,
- q0∈Q je počáteční stav,
- z0∈Z je počáteční zásobníkový symbol (čili symbol, který je při spuštění automatu uložen na zásobníku)
- F⊆ Q je množina přijímacích stavů.
Jeden výpočet přechodové funkce δ(q,a,z)=(q',w), neboli vykonání instrukce (q, a, z) →(q', w) pro q,q'∈Q, a∈A∪{λ}, z∈Z a w∈Z* znamená, že aktuální stav q se změní na q', ze vstupu se přečte písmeno a (anebo také nepřečte, v případě že a=λ) a aktuální symbol na vrcholu zásobníku z se nahradí posloupností w (třeba prázdnou či jednoprvkovou) zásobníkových symbolů (symboly zapsané vlevo se do zásobníku umístí níže než symboly vpravo). Pokud by bylo možné provést jak instrukci s a=λ, tak s konkrétním znakem, automat si vybere možnost s a=λ.
U zásobníkového automatu narozdíl od KA nepožadujeme, aby byla přechodová funkce δ definována pro všechny možné kombinace stavu, písmene a zásobníkového symbolu. Výpočet stroje se zastaví při dvou příležitostech: pro (q,a,z) není definována žádná instrukce nebo došlo k odstranění všech symbolů ze zásobníku. Všimněte si, že zásobníkový automat s (ne)vhodnou přechodovou funkcí (tedy vlastně programem) je již může zacyklit v nekonečné smyčce.
Zbývá si přesně říci, kdy je dané slovo přijato. Narozdíl od konečných automatů, u zásobníkových automatů můžeme stanovit hned dvě možnosti přijetí.
- Slovo u∈A* je přijímáno DZA M koncovým stavem, pokud se stroj M spuštěný na slovo u po konečném počtu kroků zastaví, celé slovo u je přečteno a M se nachází v přijímacím stavu. Jazykem DZA M přijímajícího stavem nazveme množinu všech slov, která M přijímá, značíme ji L(M). Množině všech jazyků, které lze rozpoznávat DZA koncovým stavem (tedy všech takových jazyků L, že pro L existuje nějaký DZA M přijímající stavem takový, že L=L(M)), se říká deterministické bezkontextové jazyky, budeme ji značit BKS.
- Slovo u je přijímáno DZA M prázdným zásobníkem, pokud se stroj M spuštěný na slovo u po konečném počtu kroků zastaví, celé slovo u je přečteno a zásobník stroje M je vyprázdněný. Jazykem DZA M přijímajícího zásobníkem nazveme množinu všech slov, která M přijímá, značíme ji N(M). Množině všech jazyků, které lze rozpoznávat DZA prázdným zásobníkem (tedy všech takových jazyků L, že pro L existuje nějaký DZA M přijímající zásobníkem takový, že L=N(M)), se říká bezprefixové bezkontextové jazyky, budeme ji značit BKZ.
Příklad: Přijímat jazyk L={0n1n; n∈N} zásobníkovému automatu nečiní potíže, narozdíl od konečného automatu (což jsme si dokázali v seriálové úloze druhé série). Setrojíme si tedy DZA M, který bude přijímat prázdným zásobníkem. Vstupní abeceda M bude A={0,1}, množina stavů Q={l, p}, zásobníkové symboly Z={z,0}, počáteční stav bude l a počáteční zásobníkový symbol z, přijímací stavy F nejsou podstatné. Sadu instrukcí (čili přechodovou funkci δ) sestrojíme takto:
| δ(l, 0, z) | = (l, 0) čte první symbol 0 |
| δ(l, 0, 0) | = (l, 00) čte další symbol 0 |
| δ(l, 1, 0) | = (p, λ) čte první symbol 1 |
| δ(p, 1, 0) | = (p, λ) čte další symbol 1 |
Pokud bychom chtěli raději přijímat koncovým stavem F={qF}, pak první instrukci změníme na δ(l,0,z)=(l, z0) (čili neodstraníme počáteční symbol hned na začátku) a přidáme ještě navíc jednu instrukci:
Uvědomíme si, že každé DZA M přijímající prázdným zásobníkem lze převést na DZA přijímající koncovým stavem, jinými slovy tedy BKZ⊆ BKS. Nový stroj bude mít jiný počáteční stav, řekněme q0', a na začátku výpočtu původní počáteční symbol na zásobníku z podloží ještě jedním pomocným symbolem, řekněme z'. To se udělá například instrukcí δ(q0',λ,z)=(q0, z'z). Dále se pokračuje v původním programu, ale dodáme ještě speciální instrukce δ(q, λ, z') = (qF, λ) pro každý q∈Q, které když uvidí na zásobníku z' (neboli zásobník původního stroje se vyprázdnil), přejdou do přijímacího stavu a vyprázdní zásobník (čímž skončí). Opačný převod však provést nelze.
Úloha 1
Ukažte, že jazyk L={0n 1m; 0<n≤ m} lze rozpoznávat DZA koncovým stavem, ale neexistuje DZA přijímající prázdným zásobníkem, který by L rozpoznával. Najděte příklad regulárního jazyka (tedy rozpoznatelného konečným automatem), který nelze rozpoznávat DZA prázdným zásobníkem (a pochopitelně zdůvodněte proč). [6 bodů]
Podobně jako u konečných automatů i u zásobníkových automatů můžeme velmi podobně zavést nedeterministickou verzi stroje (viz zadání druhé série). Nedeterministický zásobníkový automat (NZA) se od DZA liší tím, že přechodová funkce δ: Q×(A∪{λ})×Z →P(Q×Z*), kde značením P(X) rozumíme množinu všech podmnožin X, nyní vrací hned několik možností, jak může stroj zareagovat. Z nich si stroj jednu libovolnou vybere. Stejně tak pokud má stroj na výběr mezi čtením písmene a nebo jeho nečtením (a=λ), může si vybrat libovolnou možnost. Dané slovo u je přijato NZA M koncovým stavem resp. prázdným zásobníkem, pokud mezi všemi možnými výpočty nad u existuje alespoň jediný, po jehož konci je celé u přečteno a M se nachází v přijímacím stavu, resp. celé u je přečteno a zásobník je prázdný. DZA je tedy zjevně pouze speciálním případem takového NZA, kde přechodová funkce vrací vždy jednoprvkovou množinu.
Úloha 2
Narozdíl od DZA, přijímání koncovým stavem a přijímání prázdným zásobníkem je u nedeterministických zásobníkových automatů ekvivalentní. (Tedy ke každému NZA přijímajícímu prázdným zásobníkem lze zkonstruovat ekvivalentní NZA přijímajíci koncovým stavem a naopak.) Ukažte. [3 body]
Obě množiny jazyků přijímaných NZA stavem i NZA zásobníkem jsou tedy stejné. Těmto jazykům se říká bezkontextové jazyky a označíme si je BK.
Úloha 3
Sestrojte nedeterministický zásobníkový automat, který umí rozpoznávat jazyk L všech palindromů nad abecedou {a,b}. (Palindrom je slovo, které se čte pozpátku stejně jako zepředu.) Také ukažte, že jazyk L nelze rozpoznávat DZA prázdným zásobníkem. Lze dokonce dokázat, že L se nedá rozpoznávat DZA koncovým stavem. To je ale o dost obtížnější a po vás to nechceme. Pokud ovšem někdo zašle správný důkaz i této varianty, štědrý bodový bonus ho jistě nemine. NZA jsou tedy výpočetně silnější stroje než DZA. [6 bodů]
Připomínáme, že vaše řešení by měla obsahovat matematicky správné a pokud možno i formální argumenty. Nicméně jelikož zásobníkové automaty jsou už poměrně složité stroje, nebudeme již takoví puntičkáři co se týká požadavků na matematický formalismus.
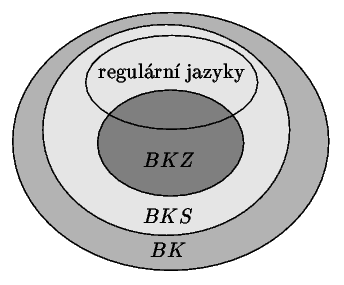
Po vyřešení všech soutěžních úloh vlastně sami ukážete tento vztah mezi bezkontextovými jazyky, deterministickými bezkontextovými jazyky a bezprefixovými bezkontextovými jazyky: