Třetí série osmnáctého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 18-3-1: Trávník
- 18-3-2: Duel
- 18-3-3: Vrah
- 18-3-4: Pochoutka pro prasátko
- 18-3-5: Hroší lov
- 18-3-6: Komplikovanější komplikátory
18-3-1 Trávník (Zadání)
Příprava na mírumilovnou hroší hostinu se zvrhla v divý boj dvou nesmiřitelných zahrádkářských skupin, které se do sebe pustily rýči, hráběmi a jinými zemědělskými stroji. Nedosti na tom, k arzenálu mimo lopatek vytáhli mnohem strašlivější zbraně sestávající z prapodivně zpotvořených tvrzení z teorie složitosti, nesčetných mýtů o rychlosti dělení a jiných zbraní hromadného ničení.
Zahrádkářská frakce S iterací na věčné časy aneb Dělení jen přes naše mrtvoly zvolila slogan Vše je konstantní. Jejich oponenti, partaj Divisoři, nechvalně proslulá jako Zběsilé vzorečky, přistoupila na taktiku Co je vyděleno, je správně.
Pojďme se podívat na jejich programy:
Obě skupinky si správně povšimly, že součet čísel v matici udává přesně množství centimetrů, o které pažit denně poroste.
Konstantníci se rozhodli posčítat si tedy čísla v matici a přičítat denní přírůstek trávníku tak dlouho, až dosáhnou požadovaného množství. Jak dlouho takový přístup trvá? Inu, představme si tu nejhorší situaci, zahradníkovu noční můru, totiž že by trávník rostl hrozně pomalu a my bychom čekali na nějaké hodně velké množství trávy. Třeba kdybychom měli trávník 1×1 s hodnotou 1 a chtěli bychom 109 trávy (máme velmi pažravé přátele). Nejhůř tedy budeme čekat O(K) času, kde K je požadované množství. A tady se konstantníci zaradovali, protože K je konstanta, tudíž máme program s konstantní časovou složitostí. Ale K není přeci žádná konstanta, kterou bychom dopředu (při psaní programu znali), nýbrž číslo, které nám přijde na vstupu. Správné je tedy říci, že program má časovou složitost lineární vzhledem ke K, tím pádem exponenciální k délce vstupu.
Divisoři si povšimli, že jestliže trávník poroste denně o s a my chceme K trávy, stačí provést triviálně K/s. Přitom velkoryse pominuli, že celočíselné dělení vrací dolní celou část a začaly se dít věci. Pro K=10 a s=10 pak program radil čekat 1 den, pro K=11 a s=10 také radil čekat 1 den (plus minus jednička, pokud někdo počítal počáteční den), prostě zmatek. Správný postup je udělat normální (neceločíselné) dělení a poté výsledek zaokrouhlit nahoru (neboli vzít horní celou část). Protože jsme informatici a neradi dělíme reálná čísla, je třeba tuto operaci nějak nasimulovat, třeba takhle (s díky Mirku Klimošovi za pěknou formulaci):
Zřejmě potřebujeme, aby tráva vyrostla ještě o (K - s). Jelikož každý den povyroste o s centimetrů, tak počet dnů, které musíme počkat, je ⌈(K-s)/s⌉. Značka ⌈ ⌉ znamená horní celou část. To lze při celočíselném dělení napsat jako ((K-s-1)/s)+1, což se rovná (K-1)/s. Tohle trvá O(N·M), neboť musíme napřed posčítat prvky v matici a pak už jen jedno dělení.
Co je tedy rychlejší? Navzdory oblíbenému argumentu "dělení je strašně pomalé" je rychlejší udělat jedno dělení oproti ohromnému množství sčítání, o kterých ani nevíme, kolik jich bude.
Někteří Divisoři pak ještě s oblibou tvrdili, že jejich program má konstantní časovou složitost. Načítání vstupu se přece nepočítá a pak už se dělá jen to jedno dělení. Nicméně i kdybychom načítání vstupu nepočítali, což se v mnohých analýzách opravdu dělá, tak stejně při výpočtu součtu prvků matice musíme sáhnout na každý prvek matice. A protože tento výpočet je neoddělitelnou součástí algoritmu, nemůžeme ho oddiskutovat jako součást vstupu. Časová složitost algoritmu je tedy O(N·M). Paměťová je tentokrát skutečně konstantní, protože nás nikdo nenutí pamatovat si celou matici, ale jenom její součet.
18-3-2 Duel (Zadání)
Hrošík vám velice děkuje za došlá řešení, avšak ať se snažil hrát kteroukoli z vámi zaslaných strategií, vždy s prasátkem remizoval. Naštěstí někteří z vás přišli na to, že hra nemá vyhrávající strategii ani pro jednoho z hráčů, ale zato existuje neprohrávající strategie pro oba hráče. Prasátko také není hloupé, a proto hrošík vždy jen remízuje. Nyní se podíváme, proč tomu tak je.
Čísla 1..9 lze jednoduše uspořádat do magického čtverce 3×3. V magickém čtverci platí, že součty trojic čísel jsou pro každý řádek, každý sloupec a obě diagonály rovny číslu 15 (tedy našemu hledanému číslu). Existuje celkem 8 různých možností, jak rozmístit čísla do čtverce, ale všechny lze vygenerovat z rozmístění na obrázku pomocí zrcadlení a otáčení čtverce o 90°.
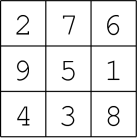
Představme si, že obě zvířátka nebudou čísla odebírat, ale místo toho si budou zaškrtávat políčka v magickém čtverci. Jistě již tušíte kam tím mířím. Zvířátka budou vlastně hrát piškvorky na mřížce 3×3 (tzv. Tic Tac Toe). Pokud se některému ze zvířátek podaří vytvořit piškvorku (tj. zaškrtnout 3 políčka v řadě, sloupci nebo na diagonále), odpovídá to situaci, kdy se jim v duelu podařilo ukořistit čísla se součtem 15.
Tím jsme ukázali, že obě hry jsou ekvivalentní. Nyní použijeme všeobecně známé tvrzení, že piškvorky na ploše 3×3 nemají vyhrávající strategii pro žádného z hráčů, a protože jsou obě hry ekvivalentní, bude toto tvrzení platit i pro náš Duel. Důkaz spočívá v rozboru všech možných tahů (s ohledem na symetrii čtverce). Podrobnější informace o tomto problému můžete nalézt třeba na stránce http://en.wikipedia.org/wiki/Tic-tac-toe.
18-3-3 Vrah (Zadání)
Zadání „obětí“ papírky je vlastně permutace a také, pro naši představu asi vhodnější, orientovaný graf. V něm vede z každého vrcholu (hráče) právě jedna hrana (k oběti) a do každého také právě jedna hrana, takže graf se skládá z několika (kruz) kružnic. Potkat se určitě mohou jen ti, co jsou na společné kružnici, kružnice ale není problém po dvou spojovat tak, že si libovolní dva lidé z různých kružnic vymění papírky. Stačilo by nám tedy kruz-1 výměn na spojení do jediné kružnice, tolik ale většinou ani nebude potřeba.
Pokud budeme do (neorientovaného) grafu s kružnicemi postupně přidávat některé zájmové (vyjadřující zájem o možnost potkání) hrany (kde přidání hrany mezi kružnice zároveň symbolizuje jejich spojení) s tím, že hranu přidáme jen tehdy, když mezi zájemci ještě nevede cesta (vede-li, už leží na kružnici – původní nebo nově vzniklé), získáme snadno postup spojování, a tedy i počet přehozů, ale za cenu složitosti O(KN).
Zkusíme to vylepšit: Uvažujme právě popsaný graf s některými zájmovými hranami. Pokud bychom do něj přidali i zájmové hrany, které jsme v předchozím algoritmu vynechali, počet komponent se nezvýší – stačí tedy pracovat s grafem, do kterého přidáme všechny hrany. Nechť má tento graf komp komponent. Navíc víme, že původní graf bez zájmových hran měl kruz komponent. Protože jedno prohození papírků může snížit počet komponent právě o jedna, hledaný počet prohození je kruz - komp. Potřebujeme tedy spočítat obě tyto hodnoty, počty komponent dvou grafů. Zvládneme to pomocí dvou prohledávání do hloubky s časovou složitostí O(K+N).
| v-1 |
| i=1 |
Navíc mohu původní hrany v kružnicích nechat jen jednosměrně orientované, při prohledávání do hloubky je jedno, jakým směrem kružnice projdeme.
18-3-4 Pochoutka pro prasátko (Zadání)
Máme šachovnici o rozměrech X ×Y a sadu K pravidel, podle nichž se prasátko umí pohybovat s určitou námahou. Krátké pozorování odhalí, že každé políčko šachovnice je jeden vrchol grafu a že mezi vrcholy vede hrana právě tehdy, pokud existuje pravidlo převádějící prasátko z jednoho vrcholu na druhý. Pak je hrana samozřejmě ohodnocena příslušným množstvím námahy. A jelikož jsou hrany kladně ohodnocené a my hledáme nejkratší cestu ze startovní pozice hladovějícího pašíka na naleziště Velké Bukvice, máme úlohu jako dělanou (ve skutečnosti opravdu dělanou) pro použití kuchařkového Dijkstrova algoritmu s haldou.
Ukázalo se ale, že naprogramovat takový algoritmus nemusí být až tak jednoduché. Někteří těžce válčili s haldou, jiní v boji podlehli a zaslali jen slovní popis algoritmu.
První otázka je, jak si vyrobit onen graf zobrazující prostor lesa. Odpověď je jednoduchá. Žádný graf není třeba vyrábět, budeme pracovat přímo nad políčky lesa a hledané hrany si budeme konstruovat přímo v okamžiku, kdybychom se v Dijkstrově algoritmu dívali na sousedy aktuálně zkoumaného vrcholu. Postupně použijeme všechna možná pravidla pro pohyb z daného políčka a podíváme se, jestli jsme se nedostali mimo les.
Druhý, horší problém, vzniká u haldy. V okamžiku, kdy v Dijkstrově algoritmu najdeme lepší cestu a přepočítáváme vzdálenost nějakému vrcholu, mění se samozřejmě jeho pozice v haldě vrcholů a haldu musíme přeskládat. Jak na to?
Můžeme si někde bokem pamatovat, kde přesně se každý vrchol v haldě nachází, a pustit na něj bublání. Pak ale musíme při jakékoli operaci s haldou každému vrcholu přepočítávat tento jeho index v haldě a to je trošku zmatek.
Jiné, jednodušší řešení je haldu nijak nepředělávat, a když nějakému vrcholu přepočítáme vzdálenost, prostě jej do haldy strčit znovu. Tak se nám některé vrcholy mohou v haldě opakovat, ale my dokážeme v Dijkstrově algoritmu při vytahování minimálního prvku z haldy snadno rozeznat, jestli jej máme zpracovávat, nebo jestli je to jen zopakovaný prvek. Poznáme to podle toho, jestli už má trvalou hodnotu.
Za jednodušší řešení ale zaplatíme. Zatímco v těžším, „přepočítávacím“ řešení se každý prvek dostane do haldy nejvýš jednou, takže halda může zabírat jen tolik místa, jaký je počet vrcholů grafu, u druhého řešení se prvky mohou dostat do haldy víckrát, konkrétně halda může být veliká jako počet hran grafu.
Dijkstrův algoritmus z kuchařky trvá O((N+M) · log N), kde N je počet vrcholů, u nás X ×Y, a M počet hran, u nás XYK. Za každou operaci s haldou násobíme logaritmem velikosti haldy. Pokud tedy použijeme haldu s přepočítáváním, dostaneme časovou složitost O(XYK · log(XY)). Jednodušší halda dá časovou složitost O((N+M) · log M) ≤ O((N+M) · log N2) = O((N+M) ·2 log N) =O((N+M) · log N), takže vlastně tutéž.
Paměťová složitost je u haldy s přepočítáváním O(XY), protože si potřebujeme pamatovat jen les a haldu na vrcholy, ale u větší haldy až O(XYK).
 Jak si všiml Pepa Pihera, náš algoritmus jde ještě vylepšit.
Malou úpravou dosáhneme toho, že v haldě bude vždy nejvýš K
prvků, čímž stlačíme složitost na O(XYK · log K). (Platí K ≤ XY,
protože pokud by pravidel bylo více, na některé políčko by se dalo dostat
pomocí více pravidel a my si můžeme nechat jenom to lepší z nich.)
Jak si všiml Pepa Pihera, náš algoritmus jde ještě vylepšit.
Malou úpravou dosáhneme toho, že v haldě bude vždy nejvýš K
prvků, čímž stlačíme složitost na O(XYK · log K). (Platí K ≤ XY,
protože pokud by pravidel bylo více, na některé políčko by se dalo dostat
pomocí více pravidel a my si můžeme nechat jenom to lepší z nich.)
V jednom kroku se Dijktrův algoritmus pokouší najít vrchol s nejmenším dočasným ohodnocením. Jinak řečeno, hledá takový nezpracovaný vrchol spojený s už zpracovaným vrcholem, že součet ohodnocení zpracovaného vrcholu a hrany z něj vedoucí je co nejmenší. Navíc vrcholy zpracováváme (trvale ohodnocujeme) podle jejich vzdálenosti od výchozího místa, tedy v neklesajícím pořadí.
Zvolme si pro tento odstavec jediné pravidlo. Kromě krajních případů ho můžeme použít z každého vrcholu. Sledujme vrcholy, které pomocí tohoto pravidla dostanou trvalé ohodnocení. V průběhu algoritmu je ohodnocení těchto zpracovávaných vrcholů neklesající. Protože jsme ho získali přičtením hodnoty pravidla k ohodnocení výchozímu vrcholu, je i ohodnocení vrcholů, ze kterých toto pravidlo používáme, neklesající. Toto jediné pravidlo tedy používáme na vrcholy v tom pořadí, v jakém je trvale ohodnocujeme.
Když víme, že každé pravidlo používáme na vrcholy v tom pořadí, v jakém je trvale ohodnocujeme, zapamatujeme si u každého pravidla, ze kterého vrcholu jsme ho naposledy použili. Když potom hledáme vrchol s nejnižším dočasným ohodnocením, každé pravidlo už má určený vrchol, ze kterého ho použijeme. Vybereme si tedy tu nejlepší kombinaci vrchol-pravidlo, tím jsme našli další vrchol s trvalým ohodnocením, a použité pravidlo „posuneme“ k dalšímu vrcholu. Tím myslíme, že příště ho budeme používat z vrcholu, který jsme v Dijkstrovi trvale ohodnotili hned po tom vrcholu, ze kterého jsme teď pravidlo používali.
V každém kroku tedy potřebujeme najít minimum z K hodnot, toto minimum odstranit a přidat místo něj jinou hodnotu. K tomu je halda jako stvořená, všechny tyto operace zvládne v čase O(log K). Navíc každou hranu zpracujeme právě jednou, čímž se dostáváme na slibovanou složitost O(XYK log K).
18-3-5 Hroší lov (Zadání)
Pomóc! Pomóóóc! Lesem zní vyplašené kvíkání prasátkovo, tak nešťastné, že ani jediné oko ostříleného programátora nezůstává suché a ani jediné srdce neustrnuté. Nezbývá nám tedy, než co nejrychleji navrhnout nějaký alespoň trochu funkční a alespoň trochu efektivní algoritmus a teprve pak se pokoušet o zlepšování.
Rychle si do bločku načrtneme základní značení: les bude mít rozměry M×N, velké H bude znamenat počet velkých hrochů, čas budeme měřit v krocích od nuly a v čase T se nebesa slitují a setmí se. Zvířátka si očíslujeme: 0 bude prasátko, 1 až H hroši; přitom každé zvířátko má svou sadu pravidel pro pohyb, jejich počet si pro i-té zvířátko označíme pi; konečně P bude celkový počet pravidel, čili P=p0+… +pH. V programu takto:
typedef struct { int x, y; } xy; // políčko
int M, N, H, T; // parametry hry
xy S[MAXH+1]; // počáteční polohy
int NP[MAXH+1]; // počty pravidel
xy Pr[MAXH+1][MAXP]; // pravidla
S hrochy v zádech budeme pro každý čas t a každé políčko (x,y) zjišťovat, kteří hroši se tam mohou vyskytovat a zda se tam může vyskytovat prasátko. Tomu budeme říkat stav lesa v čase t a budeme ho značit St.
// typ pro stav; pozor, je to pole,
// takže se předává vždy odkazem
typedef char stav[MAXM][MAXN][MAXH+1];
Jednotlivé stavy sestrojíme snadno:
V čase t=0 muže být každý hroch jen na svém počátečním políčku a prasátko jakbysmet. Pokud víme, kde může kdo být v čase t, snadno to spočteme i pro čas t+1: hroch může být na nějakém políčku v čase t+1 právě tehdy, existuje-li políčko, na němž může být v čase t a z něhož se lze na nové políčko dostat nějakým jeho povoleným pohybem. Analogicky pro prasátko, jen prasátku nedovolíme vstupovat na políčka, pro která jsme už zjistili, že na nich může být některý z hrochů.
Až toto všechno spočítáme, rozlišíme následující případy:
- V nějakém čase t<T se prasátko může vyskytovat na políčku, které je venku z lesa. Tehdy prasátko uteče a my vypíšeme cestu, která ho na toto políčko zavedla. To zařídíme třeba tak, že se budeme vracet v čase zpět a vždy zjistíme, ze kterého políčka, na kterém se prasátko mohlo vyskytnout v předchozím kroku, lze doskočit na políčko, kde stojí teď.
- V nějakém čase t<T už neexistuje políčko, na kterém by se mohlo prasátko vyskytovat. Běda, hroší spravedlnost vyhrála!
- V čase T stále existují políčka s potenciálním prasátkem. Tehdy musí jít hroši do postýlek a prasátko vyhrává timeoutem. Najdeme si tedy libovolné takové políčko a stejně jako v prvním případě sestrojíme cestu, kudy se prasátko má vydat.
Tento algoritmus se i snadno naprogramuje: budeme si pamatovat stavy St pro t=0,… ,T. Přitom St[x,y,z] bude nula nebo jednička podle toho, zda na políčku (x,y) může být v čase t zvířátko z (tedy z-tý hroch nebo pro z=0 prasátko). Stav S0 inicializujeme podle počátečních poloh, načež provedeme T dopředných kroků, z nichž každý spočítá z St stav St+1. V každém kroku stačí probrat všechna políčka, na každém všechna zvířátka a všechny jejich pohyby. Jeden krok tedy trvá čas O(MN·(p0+p1+… +pH)) = O(MNP).
Když objevíme, jak může prasátko uniknout (nejpozději po T krocích), začneme se vracet zpět a hledat konkrétní cestu. To bude probíhat ve zpětných krocích: každý takový krok dostane polohu prasátka v čase t a podle této polohy a známého stavu St-1 nalezne polohu v čase t-1. Takto se po nejvýše T zpětných krocích, z nichž každý trvá O(MNp0)=O(MNP), dostaneme do počáteční polohy, a tím je cesta ukončena.
Celkem tedy náš algoritmus doběhne za O(MNPT) kroků a k zapamatování stavů spotřebuje paměť O(MNHT). [Náš laskavý čtenář si také jistě všimne, že zapomínáme, že všech stavů není T, ale T+1, a zvířátek H+1 namísto H. Ovšem pro T>0 je T+1=O(T) a případy s T=0 můžeme ošetřit zvláštní výjimkou. V zájmu zachování duševní rovnováhy budeme všelijaké ±1 přehlížet i nadále.]
Následuje náčrt programu:
void start(stav s)
{
// vyplní počáteční stav
for (int z=0; z<=H; z++)
for (int x=0; x<M; x++)
for (int y=0; y<N; y++)
s[x][y][z] =
(x == S[z].x && y == S[z].y);
}
int vpred(stav a, stav b, xy *out)
{
// provede jeden krok vpřed ze stavu a do b
// pokud je možné utéci, zapíše do out, kam
for (int z=0; z<=H; z++)
for (int x=0; x<M; x++)
for (int y=0; y<N; y++)
b[x][y][z] = 0;
for (int z=0; z<=H; z++)
for (int x=0; x<M; x++)
for (int y=0; y<N; y++)
if (a[x][y][z])
for (int p=0; p<NP[z]; p++)
{
int xx = x + Pr[z][p].x;
int yy = y + Pr[z][p].y;
if (xx >= 0 && xx < M &&
yy >= 0 && yy < N)
b[xx][yy][z] = 1;
else if (!z && out)
{
// prasátko může utéci
out->x = xx, out->y = yy;
return 1;
}
}
// smaže prasátko z políček s hrochy
for (int x=0; x<M; x++)
for (int y=0; y<N; y++)
for (int z=1; z<=H; z++)
if (b[x][y][z])
b[x][y][0] = 0;
return 0;
}
int najdi_prase(stav s, xy *out)
{
// zjistí, zda se někde vyskytuje prasátko
for (out->x=0; out->x<M; out->x++)
for (out->y=0; out->y<N; out->y++)
if (s[out->x][out->y][0])
return 1;
return 0;
}
void vzad(stav a, xy kam, xy *od)
{
// provede jeden krok vzad
for (int x=0; x<M; x++)
for (int y=0; y<N; y++)
if (a[x][y][0])
for (int p=0; p<NP[0]; p++)
if (x + Pr[0][p].x == kam.x &&
y + Pr[0][p].y == kam.y)
od->x = x, od->y = y;
}
void pomoz_prasatku(void)
{
// hlavní program
stav S[MAXT+1];
xy cesta[MAXT+1];
start(S[0]);
int t = 1;
while (t <= T &&
!vpred(S[t-1], S[t], &cesta[t]))
t++;
if (t <= T)
puts("Prasátko uteklo:");
else if (najdi_prase(S[T], &cesta[T])) {
puts("Prasátko běhalo do setmění:");
t = T;
}
else {
puts("Hroši hodují.");
return;
}
// rekonstrukce cesty
for (int s=t; s > 0; s--)
vzad(S[s-1], cesta[s], &cesta[s-1]);
for (int s=0; s <= t; s++)
printf("(%d,%d)\n",
cesta[s].x, cesta[s].y);
}
Právě předvedené řešení by sice prasátku v nouzi stačit mohlo, ale zejména s paměťovou náročností se ještě pokusíme něco udělat, jeť obludná.
1. pokus: možných stavů je pro každý les konečně mnoho, takže pokud bude T dostatečně velké, musí se stát, že pro nějaké dva časy t a t′ bude St=St′. Co víc, stav Si+1 je pro každé i jednoznačně určen stavem Si, pročež musí také stavy v časech t+1 a t′+1 být stejné a vše se začne opakovat. Tehdy je zbytečné počítat dál a můžeme rozhodnout rovnou. Tak bychom mohli paměťovou složitost omezit na O(MNHt′), zaplatíme za to však zpomalením (zjišťovat, zda už jsme stav někdy viděli, jistě něco stojí) a hlavně se to celé vyplatí jen tehdy, pokud je T>(MN)H+1 (tolik je totiž různých možných stavů). Zkusme to raději jinak.
2. pokus: všimneme si, že pro výpočet stavu lesa v čase t+1 nám stačí znát pouze stav v čase t. Není tedy zapotřebí pamatovat si všechny stavy v minulosti a postačí nám dvě trojrozměrná pole: jedno pro stav současný, druhé pro minulý. Ale ouha, z těchto polí pak nevyčteme zpáteční cestu! Na tu skutečně potřebujeme informace o možných polohách prasátka ve všech časech, jen polohy hrochů zde už nehrají roli. Takže ke dvěma polím pro hlavní výpočet přidáme ještě možné polohy prasátka pro všechny časy, čímž paměťovou složitost zlepšíme na O(MNH + MNT) a časovou nepokazíme, je stále O(MNPT).
3. pokus (trochu zoufalý): pokud použijeme jen dvě trojrozměrná pole z předchozího pokusu, nezjistíme sice celou cestu, ale alespoň z poslední polohy spočteme polohu předposlední. Pak bychom mohli celý výpočet spustit znovu, ale zastavit ho o krok dříve a podle výsledku se dostat k předpředposlední poloze a tak dále. Tím redukujeme paměť na O(MNH), ale čas zhoršíme T-krát na O(MNPT2). To se stěží vyplatí.
4. pokus (vymyslel Peter Perešíni): zkusíme si v průběhu výpočtu zapamatovávat jen některé stavy a při zpětném průchodu dopočítávat ty zbývající mezi nimi. Řekněme, že si zapamatujeme jen každý k-tý stav, tj. S0, Sk, S2k, atd. Při zpětném průchodu si pak vždy z Sjk spočítáme k-1 dopřednými kroky stavy Sjk+1,Sjk+2,… ,S(j+1)k-1.
Celkem si tedy potřebujeme zapamatovat T/k stavů při hlavním výpočtu a k stavů při dopočítávání. Časovou složitost hlavního výpočtu jsme nezhoršili, zpětný chod jsme zpomalili o (T/k)·(k-1)<T dopředných kroků, ale to je méně, než kolik potřebuje hlavní výpočet, takže si tím neuškodíme.
Zbývá si rozmyslet, pro jakou hodnotu k získáme nejlepší paměťovou složitost. Snadno zjistíme, že to bude k=√T (až na konstantu) – pokud volíme menší k, převládá T/k, pokud větší, převládá k. Touto volbou k dostaneme paměťovou složitost O(MNH√T).
4,5. pokus (aneb všechno jde trochu zlepšit): co kdybychom předchozí řešení udělali tříúrovňově: pamatovali bychom si jedno hrubé dělení a až dojde na zpětný chod, tak bychom si toto dělení vždy mezi dvěma časy trochu zjemnili a teprve mezi časy jemnějšího dělení si znovu spočítali všechno? Po troše žonglování s čísly bychom se tak dostali k paměti O(MNH (T)1/3) a času horšímu jen v multiplikativní konstantě. Ale proč se zastavovat u tří úrovní?
5. pokus (s díky Pepovi Piherovi a jednomu ne úplně vzorovému řešení z CEOI 2005): Představme si, že už známe stav lesa St v nějakém čase t a chceme se v čase s>t prasátkem dostat na určitou pozici (x,y). Zvolíme si čas u někde mezi s a t (nejlépe v polovině) a u-t dopřednými kroky si spočítáme ze stavu St stav Su. Pak rekurzivně zavoláme tentýž algoritmus pro počáteční čas u a koncovou polohu (x,y) v čase s, čímž se dozvíme, že v čase u máme vyrazit z nějaké pozice (x′,y′) a po jaké cestě půjdeme. A nakonec ještě jedním rekurzivním voláním zkonstruujeme cestu mezi s a u a vrátíme její počáteční vrchol.
Cestu délky T tak postupně rozkládáme na menší a menší úseky, až se dostaneme k úsekům délky 1, kde stačí provést jediný zpětný krok. Rekurzi tedy můžeme popsat binárním stromem, který v kořeni bude mít úsek délky T, v prvním patře úseky délky T/2 až v log2 T-tém patře úseky délky 1. Zpracovat úsek délky l nás stojí l/2 dopředných kroků, tedy čas O(MNPl), což v součtu přes všechny úseky na jednom patře dá O(MNPT), a tudíž v součtu přes všechna patra O(MNPT log T).
Paměť potřebujeme v každém rekurzivním volání pouze na dva stavy (počítáme jich sice více, ale zajímá nás jen ten poslední, takže můžeme průběžně zapomínat), celkem si tedy pamatujeme O(log T) stavů zabírajících dohromady prostor O(MNH log T).
Toto řešeni tedy dokáže výrazně zlepšit paměťovou složitost za cenu log T-násobného zpomalení. S procedurami pro dopředné a zpětné kroky ho už naprogramujeme snadno:
void trick(xy *cesta, int t, int s, stav St)
{
// rekurzivní fce pro sestrojení cesty
if (t == s)
return;
if (t+1 == s)
{
vzad(St, cesta[s], &cesta[t]);
return;
}
// najdeme stav v polovině
stav S[2];
memcpy(S[t%2], St, sizeof(stav));
int u = t;
while (u < (s+t)/2)
{
vpred(S[u%2], S[(u+1)%2], NULL);
u++;
}
// a rekurzivně voláme pro obě části
trick(cesta, u, s, S[u%2]);
trick(cesta, t, u, St);
}
void nasel(int t, xy pos)
{
// sestroj a vypiš cestu
stav S0;
xy cesta[t+1];
start(S0);
cesta[t] = pos;
trick(cesta, 0, t, S0);
for (int s=0; s<=t; s++)
printf("(%d,%d)\n",
cesta[s].x, cesta[s].y);
}
void pomoz_prasatku_levneji(void)
{
stav S[2]; // střídavě minulý a nynější
xy pos;
start(S[0]);
for (int t=1; t<=T; t++)
if (vpred(S[(t-1)%2], S[t%2], &pos))
{
puts("Prasátko uteklo:");
nasel(t, pos);
return;
}
if (najdi_prase(S[T%2], &pos))
{
puts("Prasátko běhalo do setmění:");
nasel(T, pos);
}
else
puts("Hyeny hodují.");
}
18-3-6 Komplikovanější komplikátory (Zadání)
Mazání mrtvého kódu lze řešit několika způsoby, my si popíšeme
variantu založenou zcela na dataflow analýze. Mějme nějaké místo m
v programu. O proměnné x budeme říkat, že je na místě m živá,
pokud může být použita v živém výrazu, tedy pokud existuje v CFG cesta
z m k nějakému živému výrazu taková, že na ní není žádné přiřazení
do x. Zřejmě stačí umět pro každou proměnnou rozhodnout, kde je
živá – přiřazení assign x … je živé právě tehdy, pokud
je proměnná x živá hned za ním.
Stejně jako při propagaci konstant si pro každou proměnnou x na každé pozici v programu (pro jednoduchost můžete uvažovat skutečně všechny pozice, tj. před a po každém příkazu, ale samozřejmě se stačí omezit jen začátky a konce basic bloků) pamatovat ohodnocení. Na rozdíl od propagace konstant nám budou stačit dvě hodnoty – Ž (hodnota x na daném místě je určitě živá) a M (proměnná x by zde možná mohla být mrtvá). Na začátku hodnoty všech proměnných nastavíme na M. Bude platit, že jakmile proměnná na dané pozici nabyde hodnoty Ž, už se nikdy nezmění – to nám zajistí konečnost algoritmu.
Nyní budeme postupně zpracovávat příkazy programu, a budeme se o nich snažit dokázat, že jsou živé. Může se nám stát, že se k jednomu příkazu budeme muset vrátit vícekrát, proto si budeme udržovat frontu příkazů, které je ještě potřeba zpracovat (na začátku do fronty vložíme všechny příkazy). V každém kroku z fronty odebereme příkaz p a zpracujeme ho tímto způsobem:
- zjistíme, zda má p nějaké vedlejší efekty, pokud ano, prohlásíme ho za živý
- pokud p je přiřazení do proměnné x, a x má za p ohodnocení Ž, prohlásíme p za živý
- pro všechny proměnné, které mají za p ohodnocení Ž (kromě proměnné x, pokud je p přiřazení), nastavíme jejich ohodnocení před p také na Ž.
- pokud je p živý, ohodnocení všech v něm použitých proměnných před p nastavíme na Ž
- pokud jsme v některém z předchozích dvou kroků změnili ohodnocení proměnné z M na Ž, přidáme příkaz před p do fronty.
Poslední krok je potřeba mírně modifikovat, pokud p je na začátku basic bloku b. V tomto případě musíme nejprve pro takové proměnné nastavit ohodnocení na Ž na konci všech basic bloků, z nichž vede hrana v CFG do b, a případně přidat do fronty poslední příkazy těchto bloků. Až se situace ustálí (což poznáme tak, že se nám vyprázdní fronta), ohodnocení proměnných přesně popisuje, kde jsou proměnné živé a kde mrtvé. Živé příkazy jsou pak právě ty, o nichž jsme to někdy v průběhu algoritmu prohlásili.
Formálně lze správnost tohoto algoritmu dokázat podobně, jako správnost algoritmu pro propagaci konstant. Nám by mohlo stačit následující intuitivní zdůvodnění: Když nějaký příkaz prohlásíme za živý, také za živé těsně před ním prohlásíme proměnné v něm použité. „Živost“ těchto proměnných se pak šíří zpět po CFG, dokud nenarazí na přiřazení, které je definuje. Toto přiřazení pak prohlásíme za živé a celý postup opakujeme – časem se takto musíme dostat ke každému živému přiřazení.
Nyní ještě určíme časovou a paměťovou složitost tohoto algoritmu. Ohodnocení každé proměnné se na každé pozici změní nejvýše jednou, tedy každý příkaz budeme zpracovávat nejvýše V×, kde V je počet proměnných v programu. Z trochou šikovnosti lze celý výše popsaný postup provést v čase O(NV), kde N je velikost programu (včetně jeho CFG). Paměťová složitost je také O(NV), protože si pro každou proměnnou všude pamatujeme, zda je živá či mrtvá.