První série osmnáctého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 17. října 2005
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 18-1-1: Dimenze X
- 18-1-2: Úřad
- 18-1-3: Keřík
- 18-1-4: Dortík
- 18-1-5: Matlalové
- 18-1-6: Kompilované komplikátory
18-1-1 Dimenze X (5 bodů)
 Vědci z ústavu teoretické fyziky MFF UK si usmysleli, že zachrání svět a jednou
provždy zatočí s tajemnou a nebezpečnou Dimenzí X.
Sestrojili přístupový portál a vyslali do něj dva roboty, z nichž každý nese
slušný náklad plutonia. Jistě si sami dovedete představit za jakým účelem a
sami tušíte, že oba kusy plutonia je potřeba dát na místě k sobě.
Vědci z ústavu teoretické fyziky MFF UK si usmysleli, že zachrání svět a jednou
provždy zatočí s tajemnou a nebezpečnou Dimenzí X.
Sestrojili přístupový portál a vyslali do něj dva roboty, z nichž každý nese
slušný náklad plutonia. Jistě si sami dovedete představit za jakým účelem a
sami tušíte, že oba kusy plutonia je potřeba dát na místě k sobě.
Jaké však bylo překvapení vědců, když po odeslání robotů zjistili, že Dimenze X je pouze jednorozměrná, tedy obyčejná přímka, navíc táhnoucí se prokazatelně od severu k jihu. Do výpočtů se navíc vloudila chybička a roboti dopadli na naprosto neznámé místo na přímce, každý někam jinam. Na obou místech přistání zůstala po robotech hromada šrotu, která z nich nárazem odpadla, mimo jiné komunikační a senzorová jednotka. Paměťový obvod se také částečně poškodil, kompas naštěstí vydržel. To znamená, že roboti se spolu nemůžou nijak na dálku domluvit a jejich setkání se tak značně komplikuje. Ale Vy to přeci tak nenecháte!
 V každém kroku se robot může posunout buďto o 1 metr na sever nebo o 1 metr na jih.
Robot naštěstí pozná, že právě přechází přes hromadu šrotu (ale už nepozná, jestli
přes svou, nebo druhého robota). Kromě nákladu plutonia (který pochopitelně nesmí zahodit)
už neunese vůbec nic dalšího. Paměťový obvod je poškozený, takže čím méně si toho
bude robot muset pamatovat, tím lépe.
Navrhněte nouzovou posloupnost povelů – tedy vlastně algoritmus
(programovat ho ale nemusíte) –
pro roboty takovou, aby do sebe roboti na přímce zaručeně po nějaké době
narazili. Ale pozor, oba dva roboti dostanou jednu a tutéž posloupnost povelů.
V každém kroku se robot může posunout buďto o 1 metr na sever nebo o 1 metr na jih.
Robot naštěstí pozná, že právě přechází přes hromadu šrotu (ale už nepozná, jestli
přes svou, nebo druhého robota). Kromě nákladu plutonia (který pochopitelně nesmí zahodit)
už neunese vůbec nic dalšího. Paměťový obvod je poškozený, takže čím méně si toho
bude robot muset pamatovat, tím lépe.
Navrhněte nouzovou posloupnost povelů – tedy vlastně algoritmus
(programovat ho ale nemusíte) –
pro roboty takovou, aby do sebe roboti na přímce zaručeně po nějaké době
narazili. Ale pozor, oba dva roboti dostanou jednu a tutéž posloupnost povelů.
18-1-2 Úřad (6 bodů)
Bylo nebylo, na jistém nejmenovaném úřadě jistého nejmenovaného města v jisté nejmenované republice byli velmi líní úředníci. Lidé přicházeli se svými žádostmi, přiznáními, potvrzeními, stížnostmi a dalšími písemnostmi za úředníky, kteří s otráveným výrazem vyslechli, co od nich kdo chce. Potom se slovy „Náš úřad to přezkoumá“ spis založili do šanonu, aby ho z něj už nevytáhli až do skonání světa. Ale to jim nestačilo a po čase začali zařazovat i samotné šanony a pořadače do jiných šanonů, pořadačů, fasciklů, s deskami různých barev, a takové objemné svazky potom ukládali do police.
Jednou přišel do úřadu kontrolor. Ne ovšem proto, aby zjistil, jestli úředníci dobře vyřizují žádosti, nýbrž jestli správně archivují spisy. Stoupnul si k polici se spisy a ze zadní strany postavil nervózního ředitele, aby zleva doprava četl barvy desek a jestli je to otevírací deska nebo uzavírací. Úkolem kontrolora je zjistit, jestli jsou šanony do sebe dobře zabalené. Očíslujme si jednotlivé barvy a pokud je před číslem minus, je to deska uzavírací, jinak otvírací. Například tohle zjevně nejsou dobře zabalené desky: 4, 5, -4. Stejně tak tyto: 7, 8, -7, 8. Nicméně proti těmto nelze nic namítat: 1, 5, 6, -6, -5, -1, 6, -6.

Pomozte kontrolorovi zdeptat pana ředitele! Napište program, který odpoví, jestli desky jsou či nejsou dobře zabalené. Program dostane na vstupu přirozené číslo K, což je maximální počet barev šanonů, a počet nahlášených desek N (otevíracích i uzavíracích dohromady). Poté následuje N čísel c, 1≤ |c| ≤ K udávajících barvy šanonové desky, kladné číslo c značí otevírací desku barvy c, číslo -c uzavírací desku barvy c. Program by měl vypsat ano nebo ne podle toho, jestli jsou desky správně zabalené. Jinými slovy, pokud si různé typy šanonů představíme jako různé typy závorek, pak je Vaším úkolem otestovat, zda je zadaná posloupnost závorek správně uzávorkovaná.
Příklad: Pro K=3, N=8 a desky 2,1,2,-2,-1,-2,3,-3 by měl Váš program vypsat odpověď ano, zatímco pro desky 1,2,3,1,-1,-2,-3,-1 je správná odpověď ne.
18-1-3 Keřík (10 bodů)
Housenka běláska je neuvěřitelně žravý tvor. Když se jednou tak potulovala po zahrádce plné salátu, kedluben, řepy a spousty dalších laskomin, narazila na velmi chutně vypadající keř.
Keř sestává z význačných bodů, na kterých rostou šťavnaté lístky, a větví mezi nimi, kde neroste nic. U každého bodu je zadáno, kolik lístků na něm roste, a seznam jiných význačných bodu, do kterých z něj vede větev. Dále víte, že keř je zkrátka strom, a tedy mezi každými dvěma význačnými body vede právě jedna cesta.
Housenka by ráda začala svou hostinu v nějakém význačném bodu keře a postupně se po větvích přesouvala na jiné body, nikdy však do místa, kde už jednou byla. A chtěla by se co nejvíce najíst. Pomozte jí a napište program, který k zadanému keři najde nejvýživnější cestu v něm, tedy cestu mezi nějakými dvěma body, na které se neopakuje žádný význačný bod a která obsahuje největší možný počet lístků.
Program dostane na vstupu číslo N, což je počet význačných bodů, a N řádků popisujících jednotlivé vrcholy (očíslujeme si je 1 až N). První číslo na i-tém řádku udává počet lístků, druhé číslo počet větví v vedoucích z i-tého bodu, načež následuje v čísel udávajících, kam ty větve vedou. Program by měl vypsat na výstup nejvýživnější cestu, pokud je takových cest více, tak libovolnou z nich.
Příklad: Pro čtyři význačné body, které obsahují po řadě 1, 2, 3 a 4 lístečky, a pro větvičky 1↔2,2↔3,2↔4 je nejvýživnější cesta 3→2→4 s 9 lístečky.
18-1-4 Dortík (11 bodů)
Klub Sběratelů Pamětin právě slaví své K-té narozeniny. Proto jeho členové vytáhli ze svých nekonečných sbírek narozeninový dort s N svíčkami (jiný zrovna nedokázali najít). Rádi by na něm zapálili právě K svíček a jelikož sběratelé pamětin mají velmi vytříbené estetické cítění, musí tyto svíčky ležet ve vrcholech pravidelného K-úhelníku.
Napište pro ně program, který na vstupu dostane čísla N a K a dále polohy všech N svíček v libovolném uspořádání. Všechny svíčky leží na kružnici, takže jejich polohu můžeme jednoznačně popsat úhlem, který svírá spojnice středu kružnice a svíčky s osou x. Výsledkem programu by měl být nalezený pravidelný svíčkový K-úhelník, případně zpráva, že žádný takový neexistuje.
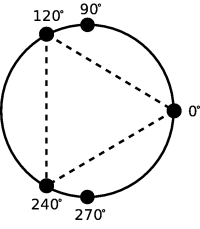
Příklad: 5 svíček na pozicích 0°, 240°, 270°, 120° a 90° obsahuje pravidelný svíčkový trojúhelník, ale neobsahuje pravidelný svíčkový čtyřúhelník.
18-1-5 Matlalové (15 bodů)
A nyní zprávy ze Země: „Institut SETI konečně potvrdil existenci mimozemského života! Frakce Marťanů a létajících talířů (MALTAL) oznámila zachycení vysílání potvrzující existenci skutečných Marťanů, kteří používají opravdové létající talíře!“ „Ty Matlalové jsou ale natvrdlí, jaké létající talíře? Budeme tam muset zaleťet a objasnit to!“
Na Zemi přistáli mimozemšťani přímo na zahradě před frakcí MALTAL. „Marťanové!“ „Matlalové! My vůbec nepoužíváme létající talíře! Dříve jsme létali na létajících kobercích, ale protože se na nich není jak držet, často jsme z nich ve vesmíru padali, a tak nyní používáme létající stoly!“
Na zahradě opravdu stály létající stoly, některé dokonce stály na ostatních (při pohledu shora se překrývaly). Ovšem díky marťanskému způsobu navigace byly hrany všech stolů rovnoběžné se světovými stranami. Protože se už ale seběhl dav, který si chtěl Marťany a jejich dopravní prostředky prohlédnout, rozhodli se Matlalové postavit kolem létajících stolů plot. Protože se ale některé ze stolů překrývají, není vůbec jasné, jak by měl být dlouhý. A protože Vás Matlalové už znají (vědí, jak jste zatočili s Dimenzí X), požádali Vás o pomoc.
Program dostane na vstupu N, počet marťanských létajících stolů, a jejich jednotlivé polohy. Každý marťanský stůl je zadán pomocí svého „levého horního“ rohu (při pohledu shora) a svou délkou a šířkou v metrech, přičemž jednotlivé stoly se mohou překrývat. Vaším úkolem je říci, kolik metrů plotu bude třeba k oplocení území, na kterém marťanské stoly přistály. Plot musí oplotit všechny zadané stoly, musí vést vždy po jejich hranici, ale nikdy nesmí vést uvnitř nějakého létajícího stolu (matematicky řečeno chcete zjistit obvod sjednocení všech létajících stolů). Počítejte s tím, že jak souřadnice, tak délky a šířky marťanských stolů mohou být reálná čísla.
Příklad: Pro N=4 a létající stoly
- levý horní roh (0,0), délka 20 m a šířka 10 m,
- levý horní roh (10,10), délka 10 m a šířka 30 m,
- levý horní roh (20,10), délka 20 m a šířka 20 m,
- levý horní roh (22.5,-12.5), délka 15 m a šířka 5 m,
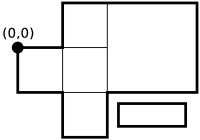
je hledaná délka plotu 180 m.
18-1-6 Kompilované komplikátory (11 bodů)
V letošním ročníku seriálu si budeme povídat o kompilátorech. Samozřejmě toho nestihneme příliš mnoho (o kompilátorech existuje několik tlustých knih a stovky článků), ale měli bychom získat alespoň obecnou představu o tom, jak kompilátory fungují.
Začněme trochou historie. Před dávnými časy se počítače programovaly přímo ve strojovém kódu – tj. programátor psal (nebo děroval) řady čísel. Napsat takto jakýkoliv rozsáhlejší program bylo samozřejmě velmi obtížné, o hledání a opravování chyb ani nemluvě. Proto se brzy objevily nástroje, které tuto činnost usnadňovaly – assembler, který alespoň umožňoval zapisovat instrukce v čitelnější formě a pojmenovat si proměnné, a později i vyšší programovací jazyky.
Jedním ze zásadních problémů překladačů programovacích jazyků byla rychlost (tedy spíše pomalost) jimi produkovaného kódu. Nějakou dobu trvalo, než optimalizace, které překladače provádí, dosáhly takové úrovně, aby výsledný kód byl srovnatelný s tím, co napíše programátor v assembleru. Po docela dlouhou dobu strašily v programátorských učebnicích poučky typu „místo 3*x pište x+x+x“, které měly kompilátoru zabránit, aby použil „drahou“ instrukci na násobení. Dnes již naštěstí takovéto obludnosti nejsou potřeba (a pouze učiní program těžším ke čtení) – dost často jsou přímo v assembleru napsané programy pomalejší než zkompilované.
Většina seriálu bude věnována tomu, jakými optimalizacemi se tohoto výsledku dosáhne. Nicméně nejprve bychom si měli popsat, jak kompilátor vypadá a s čím vlastně pracuje. Níže popsané schéma kompilátoru bylo obecně přijato a v nějaké podobě ho používají zřejmě všechny v současnosti existující kompilátory.
Prvním krokem při kompilaci je lexikální analýza. Jejím úkolem je vstup (což je nějaká posloupnost
znaků) převést na posloupnost objektů, které nesou nějaký smysl. Například, pokud je na vstupu řetězec
„bla = bla + 42“, pro překladač je nezajímavé, že je to znak 'b', následovaný znakem 'l', atd.
Výsledek lexikální analýzy by nám v tomto případě řekl, že na vstupu je identifikátor proměnné (bla),
následovaný operátorem přiřazení, dalším identifikátorem, operátorem sčítání, a číslem (42).
Výstupem tedy je posloupnost tzv. tokenů. Každý z nich má typ udávající, o jaký objekt se
jedná (zda to je identifikátor, číslo, atd.), a případně nějaké další informace (např. u identifikátorů
řetězec, udávající jeho jméno, u čísel jejich hodnotu, apod.).
Druhým krokem je syntaktická analýza. Jejím úkolem je rozebrat strukturu programu. Výsledkem
syntaktická analýzy výrazu „bla = bla + 42“ je to, že se jedná o přiřazení, na jehož levé straně je
proměnná a na pravé straně je operátor sčítání aplikovaný na proměnnou a číslo. Povšimněte si, že v syntaktické
analýze zpravidla záleží pouze na typech tokenů, nikoliv na další informacích u nich uložených – nezáleží na tom,
jak se proměnná jmenuje, nebo jaká je hodnota čísla (i když samozřejmě tyto informace nesmíme ztratit).
Výsledek se obvykle reprezentuje jako syntaktický strom. Vrcholy tohoto stromu odpovídají tokenům,
synové vrcholu pak operandům příslušného výrazu nebo příkazu. Například vrchol obsahující plus bude mít jako
syny sčítané výrazy, vrchol obsahující příkaz if bude mít jako syny podmínku, then větev a else větev.
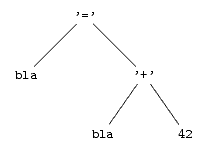
Syntaktický strom výrazu „bla = bla + 42“ vypadá takto:
Syntaktická analýza se samozřejmě provádí podle syntaxe daného programovacího jazyka. Syntaxe bývá nejčastěji zadána pomocí bezkontextové gramatiky. Co to přesně znamená, se můžete dočíst v loňském seriálu, my si pouze ukážeme příklad syntaxe jednoduchého aritmetického výrazu (obsahujícího sčítání, odčítání, násobení, dělení a závorky), ze které bychom měli získat hrubou představu:
| výraz | → | výraz '+' výraz_nás | |
| | | výraz '-' výraz_nás | ||
| | | výraz_nás | ||
| výraz_nás | → | výraz_nás '*' operand | |
| | | výraz_nás '/' operand | ||
| | | operand | ||
| operand | → | číslo | |
| | | proměnná | ||
| | | '(' výraz ')' |
Zde výraz_nás je výraz, jehož operátor má alespoň tak vysokou prioritu, jako násobení.
Tedy podle této gramatiky například operand výrazu je buď číslo, nebo proměnná, nebo
uzávorkovaný výraz.
Existují nástroje, kterým se zadá takováto bezkontextová gramatika a automaticky vytvoří kód, který provádí syntaktickou analýzu popsaného jazyka. Druhou variantou je napsat si syntaktickou analýzu „ručně“, což je o něco pracnější, ale snáze se popisuje ošetřování chyb a jiných speciálních případů.
Dalším krokem bývají jednoduché optimalizace (například zjednodušování výrazů), které se snadno provádí na syntaktických stromech. Pro většinu optimalizací je však reprezentace pomocí syntaktických stromů poměrně nevhodná. Například operandy výrazu mohou být libovolně složité a mohou mít různé vedlejší efekty (změny hodnot proměnných, volání libovolných funkcí, apod.), které činí práci s nimi dost nepohodlnou. Proto se program dále převádí do tzv. mezikódu, což bývá jazyk podstatně jednodušší, často podobný assembleru. To, jak přesně mezikód vypadá, se překladač od překladače dost liší, často se v jednom překladači používá i více mezijazyků, které se typicky čím dál tím víc blíží výslednému assembleru. Jednoduchý mezijazyk by mohl vypadat například takto:
Program je posloupnost příkazů. Příkazy jsou následující:
assignproměnná výraz – přiřadí do proměnné hodnotu výrazu. Výraz musí být jednoduchý, tedy musí to být proměnná, číslo, nebo nějaká aritmetická operace, jejíž operandy jsou buď proměnné nebo čísla. Takže výraz může být třeba x, 42, x+y, ale už x+y+1 je příliš složité.labeljméno – označuje label, na který se dá skákat.gotojméno – skočí na label se jménem jméno.ifpodmínka jméno1 jméno2 – pokud je podmínka pravdivá, skočí na label se jménem jméno1, jinak na label se jménem jméno2. Podmínka musí být jednoduchá, tj. pouze porovnání dvou proměnných nebo čísel.
Například kousek programu v Pascalu
sum := 0;
for i := 1 to 10 do
sum := sum + 2 * i;
se do mezikódu přeloží jako
assign sum 0
assign i 1
label loopbeg
assign tmp (2 * i)
assign sum (sum + tmp)
assign i (i + 1)
if (i <= 10) loopbeg loopend
label loopend
Nad takovýmto mezikódem se provádí většina optimalizací. Povšimněte si, že v mezikódu nezáleží na tom, jaký jazyk vlastně překládáme – stejný mezikód bychom dostali při překladu následujícího programu v C:
sum = 0;
for (i = 1; i <= 10; i++)
sum += 2 * i;
Všechny optimalizace nad mezikódem tedy můžeme sdílet mezi překladači různých programovacích jazyků. Část překladače, která závisí na použitém programovacím jazyce a která končí typicky překladem do mezikódu, se nazývá front-end. Část, v níž se provádí optimalizace víceméně nezávislé jak na překládaném jazyce, tak na assembleru, do nějž program překládáme, se nazývá middle-end.
Poslední částí překladače je back-end. Tato část přepisuje program z mezikódu do assembleru, a je tedy závislá na architektuře, pro kterou je výsledný kód určen (jiný back-end se používá pro počítače založené na procesorech typu x86, které asi všichni znáte, jiný pro další, „exotičtější“ procesory). V back-endu se často provádí optimalizace specifické pro danou architekturu, například scheduling (přerovnávání instrukcí tak, aby se daly provádět paralelně), přiřazování proměnných do registrů a další.
Překladač se tedy skládá z jednoho či více front-endů pro různé programovací jazyky, middle-endu, a jednoho či více back-endů pro různé architektury. Samozřejmě ve skutečnosti rozdělení nebývá takto jasné. I v middle-endu musíme například znát časy provádění instrukcí, abychom mohli dobře optimalizovat, a tedy middle-end musí něco vědět o cílových architekturách. Pokud je dobře navržen popis architektury, lze také často sdílet některé části back-endů, a některé optimalizace se tak přesouvají spíše do middle endu.
Úloha:
Abychom si pouze nepovídali, zkusíme si v této sérii prakticky napsat jednoduchý front-end
k překladači. Abychom se vyhnuli komplikacím, měl by umět pouze překládat výrazy popsané gramatikou
uvedenou v textu seriálu, do popsaného mezikódu. Výsledek výrazu by měl být přiřazen do proměnné result.
Například výraz
x * (x + y) - z / bla / neco * 5by měl být přeložen jako
assign tmp1 (x + y)
assign tmp2 (x * tmp1)
assign tmp3 (z / bla)
assign tmp4 (tmp3 / neco)
assign tmp5 (tmp4 * 5)
assign result (tmp2 - tmp5)