Čtvrtá série osmnáctého ročníku KSP
Celý leták v PDF.
 Milí řešitelé!
Milí řešitelé!
Vánoce jsou definitivně za námi. Stromeček dohořel, cukroví dojedli holubi a kapr zase přežil. Ale nezoufejte, blíží se Velikonoce. Navíc pro Vás máme přichystané (velikonoční) překvapení: první týden v dubnu se bude konat jarní soustředění! Podrobnosti a přihlášky se časem objeví na našem webu.
- Termín série: 20. března 2006
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 18-4-1: HP
- 18-4-2: Elektronické hrátky
- 18-4-3: Běh městem
- 18-4-4: Metro pro krtky
- 18-4-5: Datokopci
- 18-4-6: Komplikátorový fígl
18-4-1 HP (5 bodů)
Výpočetní centrum HP (Hippo Programmers) se obrátilo vzhůru nohama. Zmatení hrošíci pobíhají sem a tam a každou chvíli se některý z nich zastaví a usne. Není také divu. Hroši nejsou zvyklí pracovat, natož řešit složité výpočetní úlohy. Jedna taková úloha teď sužuje celou společnost HP, a protože si s tím hrošíci sami neporadí, budete jim muset poradit vy. Výpočetní centrum dostalo následující úkol.
Na vstupu máte libovolně dlouhé číslo ve dvojkovém zápisu a máte za úkol
zjistit, kolik nul bude mít takové číslo na konci, když ho přepíšeme do
desítkového zápisu. A protože hroši chtějí mít na všechno dost času (zejména
na spánek a jídlo), měl by váš algoritmus pracovat co nejrychleji.
Můžete předpokládat, že se dané číslo vejde do integeru.
Vaším cílem je vyprodukovat algoritmus, ne program, stačí tedy, když váš postup dostatečně podrobně popíšete. Na druhou stranu, za pěkný program vy vás mohla neminout i nějaká prémie :–)
Příklad: Číslo 11111010 končí v desítkovém zápisu na 1 nulu. Číslo 1010010000010000 končí na 3 nuly.
18-4-2 Elektronické hrátky (10 bodů)
Malý Martínek se jednoho dne velmi nudil. Nudil se tak moc, že už se víc ani nudit nemohl. Bloumal po bytě a hledal, čím by se zabavil. Televize byla rozbitá, hračky ho již omrzely a všechny knížky o diferenciálním počtu Martínek dávno přečetl. Při svém bloumání narazil na tatínkovu krabici plnou zvláštních broučků a při bližším prozkoumání zjistil, že se jedná o integrované elektronické obvody. Martínek si tedy vzal tatínkovo kontaktní pole a začal si hrát. Když už se mu na kontaktní pole nic nevešlo, rozhodl se, že vyzkouší, co vlastně postavil. Ale ouha. V té obrovské změti drátů a obvodů se skoro nevyznal, natož aby zjistil, jak vlastně jeho síť funguje. Už začínal natahovat moldánky, ale pak si vzpomněl, že má spoustu přátel, kteří řeší KSP, a ti mu jistě pomohou. Aby vám s tím Martínek alespoň trochu pomohl, přepsal schéma své sítě na papír a přitom si všiml, že mezi obvody není žádný cyklus. Všechny použité obvody jsou dvouvstupová logická hradla NAND. Hradlo NAND (negované AND) je hradlo s dvěma vstupy a jedním výstupem, které se chová dle tabulky. Síť má ještě několik nezapojených drátků, na které se zapojí vstup sítě, a několik drátků, které představují výstup sítě.
| Hradlo NAND: | vstup 0 | vstup 1 | výstup |
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Napište program, který dostane na vstupu schéma sítě a pak bude schopen odpovídat na dotazy typu: „Když bude tohle na vstupu sítě, co bude na jejím výstupu?“ Svoji síť vám Martínek popsal takto:
Máte celkem N hradel, ki bitů na vstupu a ko bitů na výstupu. Hradla jsou číslována od 1 do N. U každého hradla máte napsáno, kam jsou zapojeny jeho dva vstupy. Každý vstup může být zapojen buď na výstup jiného hradla, nebo na některý vstupní bit celé sítě. Dále máte seznam ko hradel, jejichž výstupy jsou zapojeny na výstupní bity celé sítě.
Příklad: Máme hradlovou síť se čtyřmi hradly, 2 bity vstupu a 1 bitem výstupu.
| Popis hradel: | hradlo | vstup 1 | vstup 2 |
| 1. | bit 0 | bit 1 | |
| 2. | bit 0 | hradlo 1 | |
| 3. | hradlo 1 | bit 1 | |
| 4. | hradlo 2 | hradlo 3 |
| Popis výstupu: | výstup | připojen na |
| bit 0 | hradlo 4 |
Pro přehlednost ještě obrázek této sítě:
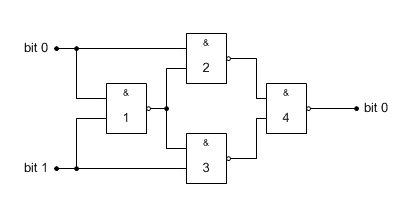
Program nyní spočítá ze zadaného vstupu výstup celé sítě:
| vstup | výstup |
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 0 |
Pozn: Pořadí bitů vstupu a výstupu je stejné jako u klasického binárního zápisu. Tedy 0. bit představuje jednotky, 1. bit dvojky, 2. bit čtyřky atd.
18-4-3 Běh městem (9 bodů)
V Kocourkově se rozhodli uspořádat velkou oslavu na počest výročí města. Městská pokladna však zeje prázdnotou, a tak museli radní vymyslet finančně nenáročný způsob oslavy. Radní si dlouho lámali hlavu, až je napadlo uspořádat pro obyvatele města závod. Zpráva se rychle roznesla do širokého i dalekého okolí a na oslavy se začali sjíždět zvědavci i z jiných měst. Jak už to ale v Kocourkově bývá, radní zapomněli domyslet trať závodu. Ulice města jsou velice zamotané, takže i místní obyvatelé mají problémy trefit tam, kam zrovna chtějí. Tajemník městské rady si je tohoto problému vědom, ale má na práci spoustu jiných věcí (koneckonců dělá většinu práce za celou městskou radu), a tak se obrátil s prosbou o pomoc na vás.

Máte danou mapu města jako neorientovaný graf, kde každá hrana představuje ulici a každý vrchol je křižovatka, nebo náměstí, do kterého ústí alespoň jedna ulice. Jeden z vrcholů je označen jako cíl celého závodu. Tajemník vás požádal, abyste z každé ulice udělali jednosměrku, a to tak, aby každý závodník, který bude dodržovat pravidla jednosměrek, doběhl po konečném počtu kroků do cíle. Závodníci mohou vybíhat z libovolného místa a na každé křižovatce se libovolně rozhodnout, kam poběží (samozřejmě jen pokud vede z dané křižovatky více ulic; pokud z křižovatky nevede ulice žádná, závodník zde musí čekat do skonání věků). Zároveň by bylo rozumné, aby závod někdy skončil, takže každý závodník se musí dostat do cíle v konečném počtu kroků, ať se na křižovatkách rozhodne pro libovolnou jednosměrku. Pokud existuje víc možných řešení, program vypíše libovolné z nich.
Příklad: Na obrázku vidíte mapu města s vyznačeným cílem a jednu z možných správných orientací:
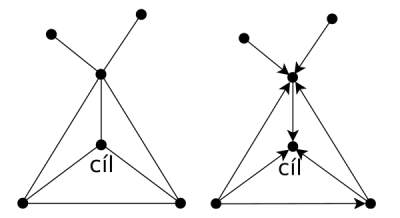
18-4-4 Metro pro krtky (10 bodů)
Baron von Maulwurfshaufen měl okolo svého sídla překrásnou zahradu v raně euklidovském slohu, které vévodil obrovský kruhový záhon plný macešek a okrasných okurek. Leč staleté prokletí rodu von Maulwurfshaufenů na sebe nedalo dlouho čekat. Na okraji záhonu se začaly objevovat zlověstné krtiny: první, druhá, třetí, čtvrtá, … až N-tá. Nedosti na tom, krtci vedou velice bohatý společenský život a chtějí své příbuzné na druhém konci záhonu navštěvovat, a tak se rozhodli, že si mezi krtinami vyvrtají metro.
Všechny tunely metra vedou po úsečkách a v téže hloubce, proto se nejspíš mnohé z nich budou protínat a v místech průsečíků bude zapotřebí postavit výhybky a zaměstnat žížaly, které je budou obsluhovat. Krtci se ovšem obávají, že v okolí nebude dostatek žížal. Jelikož krtci jsou narozdíl od cholerického pana barona milá a přátelská zviřátka (černý sametový kožíšek, drápy jako vývrtky atd., však to znáte), jistě jim rádi pomůžete zjistit, kolik žížal budou potřebovat najmout.
Napište program, který dostane zadané polohy krtin (měřené ve stupních, podobně jako jsme popisovali svíčky v úloze 18-1-4) a dvojice krtin, mezi kterými povedou trasy metra, a odpoví počtem průsečíků tras. Můžete předpokládat, že v každé krtině končí právě jedna trasa.
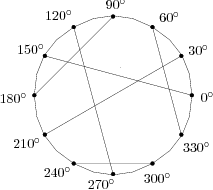 Napište program, který dostane zadané polohy krtin (ve stupních, viz obrázek)
a seznam dvojic krtin, mezi nimiž povedou trasy metra. Program pak
odpoví počtem průsečíků tras (pro náš obrázek je to 8).
Navíc můžete předpokládat, že v každé krtině končí právě jedna trasa
a že se v žádném bodě neprotnou více než dvě trasy.
Napište program, který dostane zadané polohy krtin (ve stupních, viz obrázek)
a seznam dvojic krtin, mezi nimiž povedou trasy metra. Program pak
odpoví počtem průsečíků tras (pro náš obrázek je to 8).
Navíc můžete předpokládat, že v každé krtině končí právě jedna trasa
a že se v žádném bodě neprotnou více než dvě trasy.
18-4-5 Datokopci (15 bodů)
Moderní obor nazývaný Data Mining alias Datokopectví pokračuje ve svém vítězném tažení světem. Proniká už i do vydavatelského průmyslu. Známá tiskařská firma U-tisk se rozhodla jít s dobou a místo zaměstnávání spousty redaktorů shánějících v terénu potřebné informace se jala zprávy raději dolovat.
Za tímto účelem zakoupili dvojrozměrné pole, rozdělili jej na jednotková políčka a prozkoumali, kolik lze na kterém z nich vytěžit dobrých a špatných zpráv (obojí je dáno nějakým přirozeným číslem). Vytěžené zprávy chtějí dopravovat do redakcí, kde se budou zpracovávat: dobré zprávy do redakce pohádek ležící podél celého západního okraje pole, špatné do redakce zpravodajství ležící podél celého severního okraje.
Zprávy se mají dopravovat pomocí pásových dopravníků. Na každém políčku může stát buďto pás běžící z jihu na sever, nebo z východu na západ a naloží na něj vše, co je z příslušného políčka vytěženo. Každý pás musí vést buďto přímo do redakce (je-li políčko u okraje) nebo pokračovat pásem na sousedním políčku, který vede ve stejném směru, čímž se zprávy přidají ke zprávám ze sousedního políčka.
Vaším cílem je napsat program, který po zadání výtěžností jednotlivých políček navrhne rozmístění dopravníků, aby se do redakcí dostalo co nejvíce zpráv správného druhu (dobré zprávy se ve zpravodajství nehodí, podobně jako jsou nežádoucí špatné v pohádkách). Oba druhy zpráv jsou ceněny stejně.
Příklad: Pro pole 4×4 s dobrými zprávami rozmístěnými podle prvního obrázku a špatnými podle druhého je jedno ze správných řešení na obrázku třetím (vydoluje se 98 zpráv).
| 0 | 0 | 10 | 9 | 10 | 0 | 0 | 0 | ← | ← | ← | ↑ | ||||
| 1 | 3 | 10 | 0 | 1 | 1 | 1 | 30 | ← | ← | ← | ↑ | ||||
| 4 | 2 | 1 | 3 | 0 | 0 | 5 | 5 | ← | ← | ← | ↑ | ||||
| 1 | 1 | 20 | 0 | 5 | 10 | 10 | 10 | ← | ← | ← | ↑ |
18-4-6 Komplikátorový fígl (11 bodů)
V minulé sérii jsme si ukázali, jak se dělá globální propagace konstant pomocí dataflow. Nepříjemnou vlastností tohoto algoritmu je jeho kvadratická paměťová (a tedy i časová) složitost. Jejím důvodem je to, že si hodnotu každé proměnné určujeme na začátku a konci každého basic bloku. To ovšem vypadá jako bezdůvodné plýtvání – drtivá většina proměnných nemění své hodnoty příliš často (zejména pomocné proměnné, které si vytváří kompilátor, jsou často nastavovány jen na jednom místě v programu).
Úplně ideální by bylo, kdyby toto byla pravda pro všechny proměnné. Pokud se proměnná nastaví jen jednou a pak už se nemění, stačí si pro ni pamatovat jen jednu hodnotu, protože jestliže ji na tomto jediném místě nastavíme na konstantu, musí být této konstantě rovná úplně všude. Samozřejmě, že ne všechny programy tuto podmínku splňují. Občas si dokážeme pomoct přejmenováním proměnných. Například kód
assign a 0
assign b (a + 1)
assign a b
assign c (a + 1)
ve kterém do a přiřazujeme dvakrát, lze přepsat na program
assign a1 0
assign b (a1 + 1)
assign a2 b
assign c (a2 + 1)
kde se do každé proměnné přiřazuje jen jednou. Ovšem existují programy, kde to udělat nelze. Třeba
if (a < b) 1 2
label 1
assign x 1
goto 3
label 2
assign x 2
label 3
assign i 0
assign s x
label 4
assign s (s + i)
assign i (i + 1)
if (i < 100) 4 5
label 5
assign result s
nejde přepsat tak, abychom do proměnných x, i a s nepřiřazovali dvakrát. Toto nastane tehdy, jestliže chceme někdy použít proměnnou, do které jsme předtím mohli dosadit různé hodnoty. Abychom se s tím vypořádali, přidáme si do programu takzvané φ funkce. Funkce φ se nacházejí vždy jen na začátcích basic bloků, a to v místech, kde se sbíhá víc různých definic jedné proměnné. Argumenty φ funkce odpovídají hranám, které do bloku vedou, a její výsledek je vždy roven tomu argumentu, z jehož hrany přijde provádění programu. Například výše uvedený kód vypadá po doplnění φ funkcí takto:
if (a < b) 1 2 label 1 assign x 1 goto 3 label 2 assign x 2 label 3 assign x φ(x,x) assign i 0 assign s x label 4 assign s φ(s,s) assign i φ(i,i) assign s (s + i) assign i (i + 1) if (i < 100) 4 5 label 5 assign result s
Nyní již můžeme proměnné přejmenovat tak, aby se do každé z nich přiřazovalo jen jednou:
if (a1 < b2) 1 2 label 1 assign x3 1 goto 3 label 2 assign x4 2 label 3 assign x5 φ(x3,x4) assign i6 0 assign s7 x5 label 4 assign s8 φ(s7,s10) assign i9 φ(i6,i11) assign s10 (s8 + i9) assign i11 (i9 + 1) if (i11 < 100) 4 5 label 5 assign result s8
Výsledku této transformace se říká SSA forma (kde SSA znamená „Static Single Assignment“). Nyní vás možná napadlo několik otázek, na které je nutné si odpovědět:
- Proč jsme přejmenovali i proměnné a a b, a přiřadili i proměnným s různými jmény různá čísla? Důvod je ten, že nyní můžeme na původní jména proměnných zapomenout a pracovat jen s jejich novými verzemi. Je samozřejmě praktické, aby každá verze měla vlastní číslo, protože pak se jím dají indexovat tabulky, do nichž si optimalizace ukládají pomocné hodnoty vztahující se k dané verzi.
- Přestože jsme vám to v předchozím textu zatajili, nebylo by dobré, abychom používali neinicializované proměnné. SSA forma by tedy měla splňovat to, že každé použití verze proměnné je dominováno její definicí. Na první pohled by se mohlo zdát, že například proměnná s10 toto nesplňuje (má použití ve φ funkci, která je před její definicí). Vzpomeňme si ale, že tuto hodnotu použijeme pouze tehdy, pokud přijdeme z hrany z konce bloku s návěštím 4, a v tomto okamžiku je jistě hodnota s10 definována. Často je praktické se dívat na použití ve φ funkcích tak, jako by se ve skutečnosti nacházela na hranách, jimž odpovídají (tedy použití s10 a i11 ve φ funkcích se chovají tak, jako by byly na hraně z konce bloku s návěštím 4 na jeho začátek).
- Jak SSA formu vytvořit? Existuje několik různých algoritmů, všechny však jsou poměrně netriviální a nebudeme se jimi v tomto seriálu zabývat. Pouze poznamenejme, že časová složitost těchto algoritmů bývá v nejhorším případě kvadratická (převod do SSA formy může v nejhorším případě způsobit kvadratické prodloužení kódu programu), nicméně pro běžné programy, které neobsahují mnoho složitě se chovajících proměnných, je skoro lineární.
- Jak se SSA formy zbavit? Na konci kompilace se potřebujeme zbavit
φ funkcí a verzí proměnných, abychom mohli program přeložit do
assembleru. Jedna varianta, která vás asi napadne, je prostě zahodit
čísla verzí a vrátit se k původním proměnným. To ovšem nemusí
fungovat. Například kód
assign a x assign x y assign b apo převedení do SSA formy vypadá takto:
assign a1 x2 assign x3 y4 assign b5 a1Zatím je vše v pořádku, pokud zahodíme verze proměnných, dostaneme původní program. Může se ale stát, že optimalizace nazývaná propagace kopií změní tento kód na
assign a1 x2 assign x3 y4 assign b5 x2Zahodíme-li nyní verze proměnných, dostáváme program
assign a x assign x y assign b xv němž má proměnná b má na konci chybnou hodnotu. Další jednoduchá idea je prostě považovat verze proměnných za nové proměnné, a φ funkce nahradit přiřazeními, které přidáme na příslušné hrany. Toto řešení je korektní, ale není příliš vhodné – do programu typicky přidáme mnoho přiřazení, a navíc budeme mít podstatně víc proměnných. Proto se používá „něco mezi“ – verze proměnných, které spolu navzájem nekolidují (tj. není místo v programu, kde bychom zároveň potřebovali znát hodnotu obou) slepíme do jedné proměnné. Tím se zbavíme většiny přiřazení a zbylé kolidující verze proměnných pak prohlásíme za nové proměnné.
Na závěr si naznačme, jak se dá SSA forma využít. Typicky se podstatně zjednoduší úlohy, které se dříve řešily pomocí dataflow analýzy. Například v propagaci konstant si stačí hodnotu pamatovat pro každou verzi (není třeba rozlišovat, na kterém místě). Algoritmus pak vypadá takto:
- Hodnoty všech verzí nastav na Top a vlož je do fronty.
- Z fronty odeber verzi v. Projdi všechny přiřazení tvaru
assign x něco, v nichž je v použito.- pokud
něcoje φ funkce, slej hodnoty ze všech hran - jinak vyhodnoť
něco
- pokud
- Opakujeme 2) dokud fronta není prázdná.
- Verze, jejichž hodnota je nějaká konstanta, nahradíme v programu touto konstantou a přiřazení do nich smažeme.
Protože hodnota přiřazená proměnné se změní nanejvýš dvakrát (z Top na konstantu a z konstanty na Bottom), je časová složitost tohoto postupu lineární ve velikosti programu (v SSA formě), což většinou bývá podstatně lepší, než složitost, jíž jsme dosáhli klasickou dataflow analýzou. Také implementace bývá o dost jednodušší a snáze se přidávají různá vylepšení.
Úloha
Navrhněte algoritmus pro mazání mrtvého kódu (co to znamená viz zadání minulé série) pracující s programem v SSA formě.