Třetí série dvacátého prvního ročníku KSP
Celý leták v PDF.
Řešení úloh
- 21-3-1: Kódování memgramů
- 21-3-2: Nadposloupnost
- 21-3-3: Topologie snů
- 21-3-4: Optimalizace stromu
- 21-3-5: Rozklad na součty
- 21-3-6: Pan Cowmess
21-3-1 Kódování memgramů (Zadání)
Nejprve vyřešíme jednoduchý případ, kdy má memgram 4 políčka, a pak se pustíme do případu pro obecné N.
V tabulce se 4 políčky lze přenést 2 bity následujícím způsobem: První bit informace bude xor
hodnot v prvním řádku (tedy počet jedniček v prvním řádku), druhým bitem bude xor hodnot v
prvním sloupci. Když dostaneme memgram v nějakém konkrétním stavu, podíváme se, které bity jsou
nastaveny jinak, než jak je chceme odeslat. První bit opravíme změnou na políčku b, druhý opravíme
převrácením hodnoty políčka c a pokud jsou špatně oba, stačí změnit políčko a. A pokud jsou oba
bity nastaveny správně, změníme políčko d, které nemá na zprávu žádný vliv.
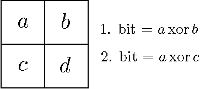
Více než 2 bity ale v této malé tabulce přenést nelze: jsou totiž 4 možné zprávy (4 možné kombinace hodnot posílaných 2 bitů), a my můžeme provést jen 4 různé akce (změnit jedno ze 4 políček). Při přenášení více bitů by bylo možných zpráv více, ale my dokážeme rozlišit jen 4.
Tento důkaz lze snadno rozšířit pro obecný případ, kdy má tabulka N políček. Umíme provést pouze N různých akcí, tedy umíme poslat nejvýše N různých zpráv, což odpovídá log2N přeneseným bitům informace.
A jak bude vypadat přenos informace většími tabulkami? Necháme se inspirovat případem N=2:
Najdeme v tabulce log2N množin políček, každá bude nést jeden bit informace v podobě xoru hodnot
na všech svých políčkách. A navíc potřebujeme, aby pro každou (i prázdnou) množinu bitů existovalo v tabulce
políčko, jehož změna způsobí změnu právě těchto vybraných bitů (a žádných jiných). Pak totiž budeme
moci opravit libovolnou kombinaci bitů, které budou v náhodně nastaveném memgramu špatně.
Stačí tedy, když o každém políčku řekneme, do kterých množin patří (které bity ovlivní jeho změna). Takovou informaci o jednom políčku si můžeme představit jako číslo ve dvojkové soustavě – i-tá číslice bude 1, pokud dané políčko leží v i-té množině (ovlivňuje i-tý bit zprávy), jinak bude 0. Aby byly množiny správně rozděleny (a bylo možné opravit libovolnou kombinaci bitů), musí v tabulce existovat všechna čísla od 0 do 2 log2N-1=N-1. To lze ale zařídit jednoduše, prostě políčka popořadě očíslujeme čísly 0 až N-1. Po převodu těchto čísel do dvojkové soustavy pro každé políčka zjistíme, které bity ovlivňuje, a můžeme jít vesele kódovat :-)
V konkrétním případě, kdy tabulka má velikost 8×8, je možné přenést log264=6 bitů informace, a lépe to už nejde.
21-3-2 Nadposloupnost (Zadání)
Nadposloupnost zřejmě hodně lidí odradila svojí komplikovaností; ten zbytek aspoň zmátla. Část problému byla v tom, že sny byly zadány jako stringy a řešení se snažila pracovat s nimi opravdu efektivně.
Nechť L je délka obou posloupností ve znacích a N je délka obou posloupností ve slovech.
Řešení používající jednoduché strcmp má složitost O(L2). S použitím trie se dá vyrobit řešení v čase O(N2 + L), které je ale zbytečně komplikované, a dá se předpokládat, že slova stejně budou krátká.
Jak takové řešení bude fungovat? Bylo by možné použít kuchařku na hledání společné podposloupnosti, a potom mezi její prvky naskládat přebytecná slova.
Ale přímé řešení je možná názornější: Budeme si pamatovat nejlepší
řešení pro prvních N slov z originálních vzpomínek a prvních M slov z
přidávaných vzpomínek (pole best/bestlen/bestbeg). Nejlepší řešení pro N/M
zjistíme na základě již spočítaných řešení pro 1… N-1/1… M-1.
Pokud slovo je společné v obou sekvencích, tak nejlepší řešení bude přidat do výstupu tuto vzpomínku, jinak máme na vyběr mezi řešením pro n-1/m a přidat originální vzpomínku a řešením pro n,m-1 a přidat vkládanou vzpomínku.
Časová složitost bude O(L2), paměťová by byla O(L+N2), kdybychom ovšem používali dynamickou alokaci.
S díky CTU Open Contestu 2008 a Josefu Cibulkovi.
21-3-3 Topologie snů (Zadání)
Skoro všechna došlá řešení se úspěšně vypořádala s problémem a snoví inženýři mohli být nadmíru spokojeni. Jak už to ale bývá, některá byla pomalejší a jiná o maličko rychlejší. Udělejme si malou vycházku do lesa a podívejme se na stromy pořádně.
Jakpak vypadá prefixový, infixový a postfixový zápis? Na obrázku máme strom s kořenem x a podstromy A a B. Tři zápisy jsou uvedeny pod ním.
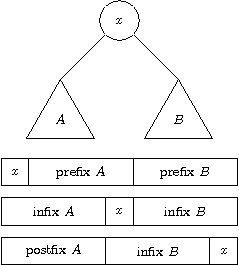
Kořenem stromu je x, které se nachází na první pozici v prefixovém zápisu. Naproti tomu v infixovém zápisu odděluje prvky levého podstromu a prvky pravého podstromu. Navíc k těmto dvěma podstromům máme i jejich prefixové zápisy. Tím jsme problém rozdělili na dva a můžeme použít pro stromy typický postup rozděl a panuj. Pro stromy se hodí obzvlášť, neboť pro ně je rozdělení na menší podproblémy naprosto přirozené, máme podstromy a elementární podproblémy mohou být listy.
Nalezneme kořen x v infixovém zápisu, třeba tak, že projdeme všechny prvky, a problém rozdělíme na dva podstromy, které budeme řešit rekurzivně. Rekurze se zastaví v listech, pro které jsou všechny tři zápisy stejné. Strom si nemusíme vytvářet v paměti, ale můžeme postfixový zápis rovnou vypisovat. Jaká je časová složitost? V každém kroku si potřebujeme vyhledat kořen v infixovém zápisu. Na to potřebujeme lineární čas v délce úseku. Pokud bude strom vyvážený, dostaneme celkový čas O(N log N), v nejhorším případě však O(N2). Analýza je velice podobná jako u QuickSortu.
Pokud bychom chtěli zrychlit výše popsaný algoritmus, potřebovali bychom zrychlit vyhledávání kořenů v infixovém zápisu. Mohli bychom si pro každý prvek stromu předpočítat, kde přesně se v infixovém poli nachází. Pro to není potřeba konstruovat žádné komplikované struktury, stačí nám si ke každé hodnotě v infixovém zápisu ještě pamatovat její pozici a poté infixový zápis utřídit. Vyhledávat pak můžeme pomocí půlení intervalu. S tímto zrychlením dosáhneme časové složitosti O(N log N) v nejhorším případě. Podaří se nám to vyřešit ještě rychleji? Co kdybychom se na věc podívali z jiného úhlu?
Co v předchozím algoritmu stálo tolik času? Lineární čas O(N) stojí procházení a vypisovaní prvků, tady zjevně algoritmus nezrychlíme. Velice drahé je však vyhledávání v infixovém zápisu, zkusíme se obejít bez něj. Vždy jsme nejprve problém rozdělili na dva menší a pak je řešili. Co kdybychom s rozdělením počkali, tedy nejprve pustili řešení na levý podstromu a až v průběhu zjistili, kde se nachází kořen v infixu. Jak toho ale dosáhnout? V infixovém seznamu se postupně budeme posouvat. Na začátku ukazujeme na jeho první prvek. Prefixový seznam procházíme. Ve chvíli, kdy narazíme v prefixovém seznamu na prvek z infixového, víme, že jeho levý podstrom máme vyřešený. V infixu se posuneme na další prvek a zbývá vyřešit pravý podstrom. Když narazíme na rodiče o jedna výše, víme, že i pravý podstrom je vyřešený, protože jsme vyřešili levý podstrom umístěný výš. Takto rekurentně dokážeme vypsat strom v lineárním čase O(N).
21-3-4 Optimalizace stromu (Zadání)
Vyberme si dva nejvzdálenější vrcholy a a b v neoptimalizovaném stromě T. Mezi nimi vede nějaká cesta P, jejíž délka je rovna průměru stromu d(T).
Pokud je optimalizace úspěšná a zoptimalizovaný strom T' má menší průměr, potom musí existovat i kratší cesta mezi a a b. A protože T' je strom, P již existovat nemůže, tedy jsme při optimalizaci museli odebrat některou hranu e z P.
Po odebrání hrany e (ale před přidáním nové) vznikly dva stromy, říkejme jim třeba A a B. Každý z nich obsahuje jeden z vrcholů a a b, nechť jsme si je tedy pojmenovali tak, aby a∈A a b∈B.
Dále si označme c a d konce hrany e ve stromech A a B.
Na pomoc těm, kteří se ztrácejí ve značení, zde je obrázek.
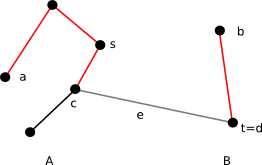
Nyní si v každém stromu najdeme střed (pro A to bude s, pro B t). Střed bude takový vrchol, že cesta do nejvzdálenějšího vrcholu téhož stromu bude nejmenší možná. Je zřejmé, že pokud jsme již správně zvolili hranu e, tak spojením s a t získáme optimální strom T' – kdybychom zvolili nějaký vrchol, který má k některému vrcholu ve svém stromě dále, vznikne tím delší cesta. Lze si všimnout, že s, resp. t, lze umístit doprostřed nejdelší cesty v A, resp. B (pokud jsou prostředky dva při sudém počtu vrcholů na cestě, pak lze vybrat libovolný z nich). Kdyby totiž vzdálenost do některého vrcholu byla větší než polovina této cesty, lze cestu prodloužit a není tudíž nejdelší. Naopak, alespoň polovinu určitě bude potřebovat libovolný vrchol na této cestě (k tomu vzdálenějšímu konci cesty).
Rozmysleme si tedy, jak správně vybrat hranu e. Už víme, že se musí nacházet na cestě P. Jaký bude průměr grafu po optimalizaci? Nová nejdelší cesta buď povede přes nově přidanou hranu, pak její délka bude:
| d(A) |
| 2 |
| d(B) |
| 2 |
Tato vznikne spojením cesty z s do nejvzdálenějšího vrcholu v A, nové hrany a cesty z t do nejvzdálenějšího vrcholu v B.
Další možnost je, že nejdelší cesta je uvnitř jednoho malého stromu, tedy d(A) nebo d(B) je větší, než nejdelší spojená cesta. Na tento případ někteří řešitelé zapomněli.
Jiní si úlohu zjednodušili tak, že odebírali prostřední hranu cesty. To, bohužel, také nefunguje (protipříkladem budiž cesta o 12 vrcholech).
Jak tedy najdeme správnou hranu? Jednoduše, vyzkoušíme všechny na cestě P. U každé hrany si spočítáme průměry stromů, které by vznikly, když bychom ji odebrali. Z nich spočítáme nejdelší cestu, která v celém stromě poté povede. Nakonec vybereme nejlepší hranu a odebereme.
Potřebujeme tedy najít napřed nejdelší cestu stromu. Strom si zakořeníme a projdeme ho do hloubky. V každém vrcholu vždy spočítáme hodnoty pro celý jeho podstrom, za použití již spočítaných hodnot ze všech synů.
Budeme počítat délku nejdelší cesty v celém podstromu a délku nejdelší cesty, která končí v kořeni aktuálního podstromu. V listech je situace jednoduchá, obě cesty mají délku 0. Pokud má vrchol syny, pro spočítání nejdelší končící v něm vezme „nejlepší nabídku“ od synů – nejdelší, končící v některém synovi. Tu poté prodlouží o 1 hranu. Nejdelší v podstromu bude buď nejdelší v podstromu některého syna a nebo spojení dvou nejdelších končících v synech. Je třeba ještě ošetřit, když je syn jen jeden (pak je druhá nabídka nulová).
Nakonec si výsledek vyzvedneme v kořeni.
Protože potřebujeme nejen délku cesty ale i cestu samotnou, budeme si pamatovat vždy některý vrchol nejdelší cesty v podstromu (nejjednodušší bude si pamatovat ten nejblíže ke kořeni) a v každém vrcholu cesty si pamatovat, kam je třeba pokračovat. Pak lze cestu jednoduše zrekonstruovat.
Proč to bude fungovat? Dokážeme indukcí. Že jsou informace pravdivé v listech je zřejmé. To, že nejdelší cesta končící do tohoto vrcholu je prodloužením jedné z nejdelších cest v listech je také vidět. A nejdelší cesta v podstromu buď prochází kořenem vrcholu, pak se skládá ze dvou končících v něm, a nebo neprochází. V takovém případě ale musí být uvnitř některého synovského podstromu.
Nyní máme tedy cestu, jak z ní vybrat správnou hranu? Potřebujeme znát průměr každého „zajímavého“ stromu (vzniklého odebráním některé hrany cesty P). Všimneme si, že délka nejdelší cesty v podstromu je průměr tohoto podstromu. Kdybychom tedy vybírali kořeny podstromů při výpočtu nejdelší cesty tak, že leží na cestě P, dostali bychom vždy jeden ze stromů odebráním hrany otec-syn.
Napřed tedy najdeme cestu P. Poté strom zakořeníme, tentokrát ve vrcholu a a prohledáme znovu. Cesta P vede z a (kořene) do některého z listů. Tedy dostaneme všechny zajímavé stromy obsahující b. Poté uděláme ještě jednou totéž, ale opačně – zakořeníme v b.
Poté projdeme hodnoty a odebereme správnou hranu. Nyní potřebujeme najít středy zbylých stromů. Ty ale, jak jsme si již všimli, leží uprostřed nejdelších cest těchto stromů. Nejdelší cesty těchto stromů máme již spočítané, tudíž středy dostaneme zadarmo.
Časová složitost je lineární. V každém vrcholu provedeme konstantně mnoho operací. Tedy, pokud porovnávání nabízených hodnot budeme považovat ještě za zpracování každého syna (každý bude s nejlepší a 2. nejlepší nabídkou porovnáván jen jednou, ve svém otci). Paměťová složitost je také lineární, více než lineárně mnoho paměti v lineárním čase nestihneme spotřebovat.
Je ale potřeba si dát pozor při načítání a pokud je v něm potřeba třídit (např. hrany podle zdrojového vrcholu), tak použít přihrádkové třídění, aby nám to složitost nezhoršilo.
21-3-5 Rozklad na součty (Zadání)
Nejeden řešitel se nyní právem raduje z velkého součtu svých bodů, neboť tato úložka byla pouze jednoduchým cvičením na rekurzi. Klíčové bylo vhodně rozmyslet, v jakém pořadí vytvářet jednotlivé součty, aby se nám žádný neopakoval víckrát.
Jeden z možných způsobů je generovat součty uspořádané vždy do monotónní posloupnosti. V našem příkladu vytváříme nerostoucí posloupnost, kterou pak vypíšeme v opačném pořadí (díky tomu je vypíšeme dokonce ve stejném pořadí jako v zadání, i když to není nezbytně nutné). Zbývá prozradit technický detail, jak jednoduše vytvářet uspořádané posloupnosti sčítanců. Zavedeme si při generování maximální číslo m a všechny zkoušené sčítance pak budou pouze z rozsahu 1 až m. Když pak sčítanec na pozici i má hodnotou k, necháme zbylé sčítance (na pozicích i+1 a vyšších) generovat s parametrem m = k, takže následující sčítance budou nejvýš tak velké, jako ten na pozici i. Nyní stačí jen přesypat naše úvahy do nějakého programovacího jazyka, trochu zamíchat a voila …
Na závěr bychom rádi poznamenali, že někteří vykutálení řešitelé se snažili optimalizovat svůj program vložením předpočítaných výsledků přímo do zdrojového kódu. Po načtení vstupu pak pouze vypsali příslušnou množinu výsledků. To je sice naprosto legitimní a v některých situacích i velmi rozumná optimalizační technika, avšak v tomto případě není nikterak užitečná. Nejpomalejším místem této úlohy je beztak vypsání výstupu a časové limity byly dostatečně velké, abyste mohli použít rekurzi. Nám nezbývá než pochválit tuto invenci a zároveň upozornit, že jsme nastavili omezení na maximální velikost odevzdávaného řešení (na 128 kB), takže příště již tato technika nepůjde použít.
21-3-6 Pan Cowmess (Zadání)
Nejprve rozluštěme, co program pana Cowmesse dělal.
Číslo zadané v registru x nejprve zapsal ve dvojkové soustavě pomocí právě 32 cifer.
Pak opakovaně hledal páry tvořené nulou a jedničkou a přepisoval je na páry dvojek.
Nakonec zkontroloval, jestli byly všechny číslice přepsané, a podle toho odpověděl.
Jinými slovy testoval, zda je v dvojkovém zápisu čísla právě 16 jedniček.
Použít na tak triviální úlohu celých 21 instrukcí je skutečně naprostá nehoráznost.
Můžeme napsat daleko jednodušší program, který bude při převodu do dvojkové soustavy rovnou počítat jedničky:
jupiii: a=x%2
b=b+a
x=x/2
if x<>0 => jump jupiii
if b<>16 => jump ooops
y=1
ooops:
Krásných 6 instrukcí by si zasloužilo potlesk, ale vavřínový věnec ještě ne. Stačí jich totiž pouhá polovina. Dopomůže nám k tomu starý dobrý operátor bitové selekce, který nám už nejednou nečekaně zamíchal karty.
Pokud spočítáme x@x, získáme číslo, které obsahuje tytéž jedničky
co x, jenže „sklepané doprava.“ Pak už jen toto číslo porovnáme s číslem
65535 (16 jedniček umístěných úplně vpravo) a máme vyhráno:
a=x@x
if a<>65535 => jump oooops
y=1
oooops:
Po tomto skandálním odhalení již zbývá jen popřát panu Cowmessovi, aby mu jeho zákazníci snížili odměnu na polovic za každou přebytečnou instrukci :)