Čtvrtá série dvacátého prvního ročníku KSP
Celý leták v PDF.
Řešení úloh
- 21-4-1: Dláždění šachovnice
- 21-4-2: Dosah kouzla
- 21-4-3: Stavění robota
- 21-4-4: Heslo
- 21-4-5: Znaky
- 21-4-6: Nejtěžší číslo
21-4-1 Dláždění šachovnice (Zadání)
„Právě jste splnili kvalifikační test na soutěž o Nejlepšího crackera roku 2009!“ Podobnou zprávu by obdržela většina řešitelů této úlohy. Naopak co místy pokulhávalo byl popis řešení. Pojďme se tedy na celý problém šachovnice podívat pořádně.
Každou šachovnici o rozměru 2N lze pokrýt L-ky bez jednoho libovolného políčka a budeme to dokazovat matematickou indukcí. Pro N=1 máme šachovnici 2 ×2 a tu snadno vyplním jedním L-kem. Pro N > 1 celou šachovnici rozdělíme na čtvrtiny (o straně 2N-1) a rádi bychom využili indukčního předpokladu. V jedné čtvrtině se nachází chybějící políčko a tuto čtvrtinu umíme z předpokladu celou vyplnit L-ky. Zbývá nám ještě vyplnit zbývající tři čtvrtiny. Abychom mohli nasadit indukční předpoklad, musíme z každé čtvrtiny vybrat jedno políčko, které nevyplníme. Pokud vybereme tři rohová políčka, jak je naznačeno na obrázku, jsme je schopni zaplnit jedním L-kem. Zbytek každé čtvrtiny potom umíme vyplnit z indukčního předpokladu. Tím jsme nalezli vyplnění celé šachovnice o velikosti 2N a důkaz je dokončen.
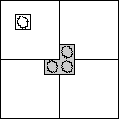
Důkaz nám říká, jak vytvořit rekurzivní algoritmus, který bude vyplnění přímo hledat. Stačilo by napsat rekurzivní funkci, která by dostala velikost šachovnice a pozici vykousnutého políčka a vrátila pokrytí L-kami. Časová složitost algoritmu je počet políček šachovnice, tedy O(22N) a rychleji to ani nejde, protože pozici přesně tolika L-ek musíme popsat. Psát však do řešení přímo program nebylo zapotřebí.
21-4-2 Dosah kouzla (Zadání)
Úloha je zcela zřejmá. Prostě ke každému vrcholu projdu všechny ostatní a spočítám vzdálenosti. Z nich vybrat největší je cvičení první hodiny programování. Časová složitost je zcela očividně O(n2).
Ale moment, 9 bodů za dva jednoduché cykly v sobě? To by se KSP dopustilo urážky na cti všech řešitelů. To půjde lépe.
Toto řešení by určitě fungovalo na libovolnou množinu bodů. Tak proč je zadaný sklep konvexní? Všimneme si, že když se posadíme do jednoho vybraného rohu k Mírielovi, od nás doleva vyběhne krysa a poběží po obvodu, tak se bude napřed stále vzdalovat, než doběhne do nejvzdálenějšího rohu, a potom už se zase bude pouze přibližovat. Jinými slovy, posloupnost vrcholů je v první části rostoucí a v druhé klesající.
| 1 |
| 4 |
Pokud takto nalezneme nejvzdálenější vrcholy pro každý vrchol, zlepšíme si časovou složitost na O(n· log n). S tím se ale ještě nespokojíme.
Když máme spočítaný nejvzdálenější vrchol od vrcholu, ve kterém právě sedíme a přesedneme si o jeden vrchol po směru hodinových ručiček (trochu obtížná představa na dobu, kdy byly hodiny přesýpací), co se stane s nejvzdálenějším vrcholem? Buď bude stále na tom samém místě, nebo se posune také po směru hodinových ručiček (nevíme ale, jak daleko). A vida, to přímo nabádá k tomu na tom založit algoritmus.
Na začátku tedy nějak seženeme nejvzdálenější vrchol k prvnímu vrcholu. Poté si (n-1)× „přesedneme“. Tím jakoby jednou oběhneme celé sklepení. Přestože nevíme, jak daleko se při každém přesunu pohne nejvzdálenější vrchol, po celém kolečku určitě skončí na stejném místě a nikdy nás nepředběhne (ty by nás musel dohnat a vrchol sám sobě nejvzdálenější být nemůže). Tedy, oběhne celé sklepení také právě jednou. Toto obíhání má tedy složitost O(n). Pokud stihneme spočítat nejvzdálenější vrchol v čase O(n), tak jsme vyhráli. Rychleji to už určitě nepůjde, načtení vstupu nám zabere alespoň takovéto množství času.
Co se týče paměťové složitosti, stačí nám pamatovat si jednotlivé vrcholy.
Ještě si lze všimnout, že si při porovnávání můžeme zcela odpustit odmocňování, neboť odmocnina z kladných čísel je rostoucí a tedy √a < √b ⇔a < b.
21-4-3 Stavění robota (Zadání)
Netrpaslická nebyla jen velikost Boendalova čísla, ale i obtížnost této úlohy. Provolejme třikrát sláva těm řešitelům, kteří se namočení do algebry nezalekli, a pojďme si osvětlit řešení.
| ( | N | ) |
| K |
| ( | N | ) |
| K |
pak
| ( | N | ) |
| K |
Tento zápis je pro kombinační čísla přirozenější, neboť vystihuje lépe jejich podstatu – kombinační číslo je počet K-tic, které můžeme vybrat z N prvků, pokud neuvažujeme opakování. A přesně tak počítá i vzorec H/K!. Nejprve vybereme první prvek K-tice, na to máme N možností, pak zvolíme druhý, to máme N-1 možností (ten první znovu vybrat nemůžeme) a tak dále, až vybereme poslední, K-tý, na něj máme N-K+1 možností. Nicméně tímto výběrem jsme si porušili druhé pravidlo – některé K-tice se nám tam opakují. My ale víme, které a kolikrát. Tímto taháním prvků jsme vybrali každou K-tici právě tolikrát, kolik je zpřeházení (permutací) K prvků. Například pokud vybíráme trojice z prvků {1 … 6}, pak trojici (1,2,3) jsme vybrali ještě jako trojice (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). Abychom všechny tyto případy zahodili, postačí nám celé číslo H vydělit počtem permutací na K prvků, a jak všichni ví, těch je K!.
Nám se tenhle zápis bude hodit, protože dělení modulo se chová hezky pří sčítání a násobení. Bota nás bude tlačit jen tehdy, když budeme chtít spočíst H/K!, neboť celočíselné dělení při operacích se zbytky k dispozici nemáme. Budeme si jej muset „odsimulovat“.
Půjdeme na to přes prvočíselné reprezentace, kterých se každý nabažil na základní škole – rozložíme zadane kombinacni číslo na mocniny prvočísel. Začneme zlehka, rozkladem součinu H. Nejprve si najdeme Eratosthenovým sítem všechna prvočísla od 1 do N. U čísel složených v tomto rozsahu si ještě poznačíme, jaké největší prvočíslo je dělí (to nám síto udělá takřka samo).
S prvočísly po ruce již můžeme rozkládat. Budeme si udržovat aktuální rozklad čísla (který nemusí být prvočíselný, například 360 = 72 ·5), setříděný podle základů. Tento rozklad si budeme pamatovat v poli, kde hodnota Z-tého prvku je rovna exponentu E takovému, že ZE je přítomno v našem rozkladu. Tento seznam rozkladů budeme postupně drolit na menší kousky.
Vezměme největší neprobraný základ Z a odpovídající exponent E. Je-li Z číslo složené, pak se podíváme do síta a najdeme největší prvočíslo P, které Z dělí. Tím se nám rozloží ZE na PE ·(Z/P)E. Obě čísla jsou menší než Z, přidáme je tedy s odpovídajícím exponentem do rozkladu a pokračujeme dále. Je-li Z prvočíslo, pak mohu tento základ a exponent vzít jako hotový (a přejdu k menšímu základu).
Pro náš příklad bude rozklad probíhat takto:
| 360 | = 721 ·51 = 241 ·51 ·31 = 81 ·51 ·32 = |
| =51 ·41 ·32 ·21 = 51 ·32 ·23. |
Použití těchto neúplných rozkladů se nám velice hodí – algoritmus totiž může rozložit libovolné číslo zadané součinem, a přesně takové je H, které rozložit potřebujeme. Nyní přišel čas vyřešit dělení číslem K!. To můžeme udělat chytrým trikem – už dopředu víme, že výsledek bude celočíselný. Začněme tedy s následujícím rozkladem:
| ( | N | ) |
| K |
Rozklad je to korektní a algoritmus nám určitě neporuší, neboť jakmile budeme rozkládat čísla menší než K, už jsme rozložili všechna větší než K, a tedy (díky celočíselnosti výsledku) nikde nemůžeme narazit na záporný exponent.
| ( | N | ) |
| K |
| ( | N | ) |
| K |
| = p1l1 ·p2l2 ·… ·pklk ( mod R) = | ||||
| = (p1l1 ( mod R) ) ·(p2l2 ( mod R) ) ·… | |||||
| … ·(pklk ( mod R) ) ( mod R) |
| N |
| k=0 |
| ( | N | ) |
| k |
Začneme od 0, p1 mod R uložíme jako základ. Pak v každém kroku přistoupíme k další mocnině. Nejprve si ověříme, jestli tato mocnina zrovna v našem rozkladu figuruje, a pokud ano, číslo, kterým máme přinásobit výsledek, vypočítáme snadno z předchozího: p2a = p2a-1 ·p2a-1.
A tím jsme hotovi! Ukázali jsme si, jak spočítat modulo mocninu velkého prvočísla, tyto výsledky vynásobíme dohromady pro každé prvočíslo, které se účastnilo rozkladu kombinačního čísla a celkový součin vypíšeme na výstup (nezapomeneme v průběhu dělit modulo R, aby nám výsledek nepřetekl).
Zbývá prohodit pár slov o časové a paměťové složitosti. Na rozklad na prvočísla jsme potřebovali dvě pole o N prvcích, zbytek se dá zvládnout jen s pár integery. Paměťové nároky jsou tedy O(N). Co se týče nároků časových, bylo by třeba spočítat, jak rychle proběhlo hledání prvočísel Eratosthenovým sítem. To zde nebudeme dokazovat, pouze poznamenejme že je to O(N log log N). Co se týče druhé části algoritmu, bude asymptoticky alespoň O(N log N). Na optimalitu si nároky neděláme, neboť u teorie čísel skoro vždy platí, že můžeme nasadit lepší síto a dosáhneme asymptoticky lepšího výpočtu.
Dík patří Zbyňkovi Faltů za vzorové řešení!
21-4-4 Heslo (Zadání)
K dané permutaci s prvky, které se mohou opakovat, lze nalézt následující v lineárním čase s její délkou (stačí najít nejdelší nerostoucí konec, cifru před ním prohodit s nejbližší vyšší z onoho konce a ten pak obrátit); K-násobné zopakování tohoto postupu vede k řešení úlohy, leč v čase O(KN), přičemž K by mohlo být poměrně velké i pro malá N, takže se pokusme o rychlejší algoritmus.
Kdybychom chtěli najít K-tou permutaci v lexikografickém uspořádání od začátku (tedy ne od nějaké dané na vstupu), vezmeme si nejprve tu nejnižší (cifry uspořádané vzestupně) a podíváme se, za jak dlouho se změní první cifra. Zřejmě se před tím musí vystřídat všechny permutace, které na ni začínají, a těch je tolik, kolik je permutací zbývajících cifer (označme tento počet P). (P+1)-ní permutace tedy vypadá tak, že na prvním místě je druhá nejmenší cifra a zbytek je opět setříděný vzestupně (rozmyslete si, že od první permutace se liší jen prohozením dvou cifer).
Pokud je K≤ P, cifru na prvním místě měnit nepotřebujeme a jen zopakujeme týž postup pro permutaci zbylých čísel. V opačném případě zaměníme první cifru s nejbližší vyšší, od K odečteme P, jakožto počet permutací, které jsme přeskočili, a opět můžeme postupovat stejně (podívat se, jestli dalším změnou na prvním místě K „nepřeskočíme“, a buď příslušné prohození udělat, nebo jít na další pozici) dokud K nesnížíme na 0.
Popsaný postup však funguje, jen když máme za cifrou, s níž právě pracujeme, cifry seřazené. Všimněme si ale, že stejně lze cifry i snižovat: pokud máme permutaci začínající na nějakou cifru, za níž jsou cifry již uspořádané, můžeme tu první prohodit s nejbližší nižší, čímž se dostaneme zpět o počet permutací na těchto cifrách bez té, kterou jsme dali na začátek.
Půjdeme tedy odzadu a cifru na každé pozici budeme postupně vyměňovat za menší až na tu nejnižší s tím, že cifry za ní jsou vždy seřazené (na začátku – pro pozici na konci – to platí triviálně a po skončení úprav tuto podmínku zřejmě rozšíříme i na aktuální pozici); zároveň budeme příslušně zvyšovat K. Ve chvíli, kdy K bude menší než počet permutací od aktuální pozice do konce, znamená to, že cifry nalevo měnit už nepotřebujeme a stačí jen najít K-tou permutaci na cifrách, které jsme prošli.
Abychom vždy nejbližší vyšší cifru k té aktuální našli rychle, místo „přeskládaného“ konce si budeme pamatovat počty jednotlivých cifer, které jsme viděli, což také stačí k tomu, abychom věděli, jak má vypadat.
Zbývá si už jen rozmyslet, jak zjišťovat počty permutací. Jelikož se cifry mohou opakovat, musíme N! ještě vydělit faktoriály počtů jednotlivých cifer. Počítat to pokaždé celé by stálo příliš času, ale naštěstí vždy potřebujeme jen drobnou úpravu, pokud do permutace délky n přidáváme nějakou cifru c, počet permutací stačí vynásobit (n+1) a vydělit novým počtem cifer c; analogicky pak pro odebírání a vyměňování cifer.
Kromě načtení vstupu projdeme celou permutaci nejvýše dvakrát a pro každou pozici potřebujeme jen konstantní čas, takže časová složitost je O(N), stejně tak i paměťová. To ovšem za předpokladu, že čísla, se kterými budeme pracovat, budou dostatečně malá na to, abychom čas spotřebovaný na jednotlivé operace mohli za konstantní považovat. Nicméně, jak bylo naznačeno v úvodu, počty permutací mohou být poměrně velké; v případě permutací deseti cifer by jich mohlo být O(10N) a na potřebné výpočty s takovýmito čísly by byl nutný čas O(log 10N)=O(N), což by vedlo na celkovou časovou složitost O(N2).
21-4-5 Znaky (Zadání)
Úlohu vyřešíme jednoduchým algoritmem: v každém kroku přečteme jeden znak ze vstupu, převedeme ho do nějaké vhodné reprezentace a postupně ho porovnáme se všemi dosud přečtenými jedinečnými znaky. Pokud se neshoduje s žádným z nich, přidáme ho do seznamu. Protože nám v této úloze jde hlavně o paměťovou náročnost, soustředíme se na to, jak reprezentovat znaky v paměti co nejúsporněji.
Vzhledem k tomu, že v každém řádku znaku je vybarvený právě jeden pixel, nabízí se řešení ukládat znak jako posloupnost N čísel s hodnotami 1 …N, kde i. číslo udává, v kolikátém sloupci i. řádku je vybarvený pixel. Kolik bitů bude jeden takovýto znak zabírat? Na každý řádek potřebujeme ⌈ log2 N⌉b, na celý znak tedy N ·⌈ log2 N⌉b. Abychom takovéto velikosti opravdu dosáhli, nemůžeme ukládat každý řádek do samostatného prvku pole, ale budeme znak v této reprezentaci chápat jako posloupnost bitů, které rozdělíme po osmi a uložíme do pole bytů. Na konci pole pak zbude až sedm nevyužitých bitů, ale s tím už nic neuděláme. Časová složitost tohoto řešení je O(K ·(N2 + KN)), protože každý z K znaků nejdříve načtu v čase O(N2) a pak porovnám s až K přečtenými znaky řádek po řádku. Lepší časové složitosti by šlo dosáhnout třeba použitím binárního vyhledávání, ale o čas nám tentokrát moc nejde.
| N-1 |
| i=0 |
| N |
| i=1 |
Zatím jsme ještě nevyužili toho, že na každé diagonále je vybarvený nejvýše jeden pixel. Použijeme stejný postup jako v předchozím případě, jenom pro každý řádek budou povolené ty pixely, pro které sloupec a obě diagonály, na kterých leží, neobsahují zatím žádný pixel. Výše uvedený znak tak můžeme přepsat jako 2/5, 2/2, 2/2, 1/1, 1/1 (5 b). Celková velikost takto zapsaného znaku může být různá i pro dva znaky se stejným N. Časová složitost těchto dvou řešení, využívajících povolené sloupce, je O(K ·(N2 + KN2)) = O(K2 N2). Zhoršení oproti první variantě je způsobené tím, že při porovnávání znaků musíme navíc pro každý řádek znaku ze seznamu už přečtených projít seznamy povolených sloupců, abychom zjistili, kolik bitů máme přečíst při čtení následujícího řádku.
Další možností, jak ještě snížit paměťové nároky je použití trie, ale my zkusíme něco jiného: řešení, které má ještě menší paměťové nároky, ale na druhou stranu zase velkou časovou složitost. Jeho myšlenka je velice jednoduchá: všechny možné znaky si očíslujeme a pro každý znak si budeme pamatovat jen jeho číslo. Pokud je možných znaků M, tak každý z nich bude zabírat ⌈ log2 M ⌉b. Jeden znak ani do méně bitů zapsat nejde, protože pak by možných zápisů bylo méně než různých znaků. Když teď do seznamu přečtených jedinečných znaků ukládáme přímo čísla, mohli bychom, podobně jak jsme to už dělali, počítat s tím, že číslo, které se v seznamu už vyskytlo, tam znovu nebude. Jde to ale líp. Tentokrát nám totiž nezáleží na pořadí a tak si můžeme tento seznam udržovat setříděný. Když v seznamu najdu číslo x, tak vím, že za ním musí následovat číslo mezi x+1 a M, takže na jeho uložení bude stačit ⌈ log2 (M - x) ⌉b. Jinou variantou, jak si přečtené znaky ukládat je posloupnost M bitů, kde i. bit určuje, jestli jsem už přečetl znak s číslem i. Rozumným kompromisem mezi těmito dvěma řešeními je použít ze začátku seznam znaků a jakmile jeho velikost překročí M bitů, přejít na druhou variantu. Jak ale vlastně určíme číslo znaku, který dostaneme na vstupu? Snadno, procházíme postupně všechny permutace N čísel a pokud některá z nich vyhovuje definici znaku, započítáme ji. Pokud narazíme na tu z nich, která je shodná se zpracovávaným znakem, známe jeho číslo. Ještě před přečtením prvního znaku ze vstupu ale musíme podobným způsobem projít všechny znaky, abychom věděli, kolik jich je celkem a kolik bitů tak budeme potřebovat na jeden znak. A nakonec časová složitost: O(N N! + K (N N! + N!)) = O(K N N!). Na začátku totiž spočítáme včechny možné znaky a pak pro každý znak na vstupu určíme jeho číslo a v případě první varianty jej porovnáme s už přečtenými unikátními znaky, kterých nemůže být víc než N!. Takto velká časová složitost samozřejmě způsobí praktickou nepoužitelnost popsaného algoritmu už i pro relativně malá N.
21-4-6 Nejtěžší číslo (Zadání)
Začneme podúlohou b), neboť nejtěžší číslo bylo nakonec překvapivě lehké :-)
Stačí si totiž vzpomenout na trik z řešení Pana Cowmesse (úloha 21-3-6): pomocí x@x
„sklepeme“ všechny jedničky v čísle směrem k nejnižšímu řádu. Pak si ještě
všimneme toho, že číslo a je těžší než číslo b právě tehdy, když a@a je větší
než b@b, a řešení je nasnadě:
sem: a = A[n] @ A[n]
if a<=m => goto tam
m = a
y = A[n]
tam: n = n-1
if n>0 => goto sem
Program pro n čísel použije 4n+2m instrukcí, kde m říká, kolikrát se během procházení pole zvýší váha čísla. To se může stát nejvýše 32-krát, takže můžeme počet instrukcí odhadnout shora výrazem 4n+64.
Toto řešení můžeme ještě zrychlit (díky, Jitko!), když si uvědomíme, že si místo hodnoty zatím nejtěžšího čísla a jeho sklepané verze stačí pamatovat pozici takového čísla ve vstupu:
sem: B[n] = A[n] @ A[n]
if B[n]<=B[m] => goto tam
m = n
tam: n = n-1
if n>0 => goto sem
y = B[m]
Tak počet provedených instrukcí snížíme na 4n+m+1 ≤ 4n+33.
Podúloha a), tedy zvážení jednoho čísla, byla naopak lehce překvapivá :-) Nejrychlejší známý program má totiž přibližně 2·109 instrukcí, z nichž se ovšem pro každý vstup provede nejvýše pět.
Jak funguje? Nejprve si zadané číslo sklepeme a pak rozebereme 33 případů, které mohou nastat. To bychom přímočaře zvládli 32 podmínkami nebo pomocí půlení intervalu 6 podmínkami. Ale my raději nepoužijeme podmínku žádnou: Využijeme toho, že parametr instrukce skoku může být nejen konkrétní číslo (či návěští), ale také obsah registru, a jedním skokem se přesuneme na správné místo v programu, které pouze vrátí výsledek. Vypadat to bude takto (v závorkách jsou napsány adresy instrukcí):
(0) z = x@x
(1) z = z+4
(2) jump z
(3) w = 32 // při z=2^32-1
(4) jump hotovo // při z=0
(5) w = 1 // při z=1
(6) jump hotovo
(7) w = 2 // při z=3
(8) jump hotovo
...
(11) w = 3 // při z=7
jump hotovo
... ...
(2^31+3) w = 31 // při z=2^31-1
hotovo:
(Všimněte si, že x@x stále potřebujeme, protože kdybychom chtěli rozebrat
úplně všechny případy, nevešel by se program do 232 instrukcí, které
dovedeme adresovat.)
Jako zákusek přidáváme ještě řešení, které si vystačí s 12 instrukcemi
bez jediného skoku. Konstanty začínající 0b jsou dvojkové. Zkuste
přijít na to, proč funguje:
y = x & 0b10101010101010101010101010101010
x = x & 0b01010101010101010101010101010101
y = y >> 1
x = x + y
y = x & 0b00110000110000110000110000110000
z = x & 0b00001100001100001100001100001100
x = x & 0b11000011000011000011000011000011
y = y >> 4
z = z >> 2
x = x + y
x = x + z
w = x % 63