Druhá série dvacátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 23-2-1: Balíčky balíčků
- 23-2-2: Zastavení
- 23-2-3: Projížďka
- 23-2-4: Plánování
- 23-2-5: Zaměřování
- 23-2-6: Testovací
- 23-2-7: Regulomaty
23-2-1 Balíčky balíčků (Zadání)
Naše úloha se docela podobá problému batohu (viz kuchařku), takže by nás mohlo napadnout použít modifikovanou verzi algoritmu, kterým se řeší.
Postupně procházíme celá čísla od nuly vzhůru a pokud jsme právě na hodnotě, kam se umíme dostat, tak projdeme všechny nabídky a pro každou z nich si poznačíme, že se umíme dostat na hodnotu, která je součtem této nabídky a hodnoty, na které právě jsme. Na začátku víme jenom to, že se umíme dostat do čísla nula. Takhle postupujeme, dokud se nedostaneme do čísla, které je větší nebo rovno H, a máme řešení.
Tenhle postup sice funguje, ale dosti pomalu. K rychlejšímu algoritmu dojdeme, když si uvědomíme, co to znamená, že každou nabídku můžeme použít, kolikrát chceme – to, že kdykoliv umíme poslat x kg, tak umíme poslat i x+kN kg pro jakékoliv nezáporné celé číslo k (N kg je totiž hmotnost nejmenší nabídky).
Díky tomu si můžeme pole hmotností přeuspořádat do tabulky o N sloupcích. Políčko na i-tém řádku j-tého sloupce pak představuje (i ·N + j) kg.
K vyplňování této tabulky bychom mohli použít stejný postup jako před chvílí, ale my si ho upravíme tak, že když jsme na nějakém políčku a umíme se dostat do nějakého políčka nad ním (číslo sloupce je stejné, číslo řádku menší), tak si poznačíme, že se umíme dostat i do aktuálního políčka, ale už nemusíme zjišťovat, kam se odsud můžeme dostat s použitím různých nabídek.
To proto, že pokud se na nějaké políčko umíme dostat z aktuálního použitím nabídky x kg, tak se tam umíme dostat i ze zmíněného políčka nad ním. A to nejdříve použitím nabídky x kg a následně několikanásobným použitím nabídky N kg.
Tuto tabulku si ale nemusíme pamatovat celou. Stačí si pro každý sloupec pamatovat, který je první řádek v tomto sloupci, na který se umíme dostat.
Tento seznam sloupců pak procházíme dokola podobně, jako jsme předtím procházeli celou tabulku – jeden průchod seznamem odpovídá průchodu jedním řádkem v tabulce.
Navíc ani nemusíme procházet seznamem slouců tolikrát, kolik řádků bychom prošli v tabulce. Jakmile se jednou umíme dostat do sloupce, který obsahuje cílové políčko, tak víme, že se umíme dostat až tam.
Pro určení výsledné kombinace balíčků si musíme pro každý sloupec zapamatovat, s použitím jakého balíčku jsme se tam dostali.
Samotnou výslednou kombinaci určíme tak, že nejdříve započítáme nabídku N kg tolikrát, kolik řádků by činil rozdíl v tabulce mezi cílovým políčkem a políčkem, kam se umíme dostat. Následně procházíme sloupce podle toho, pomocí kterého balíčku jsme se do něj dostali, dokud se nedostaneme do nultého sloupce. Všechny balíčky, které jsme na této cestě použili, započítáme také a máme kýžený výsledek.
Jakou má tento algoritmus složitost? Paměťová je O(N) – nejvíce zabírá seznam sloupců a těch je N.
S časovou složitostí je to složitější. Procházení nabídek provádíme nejvýše jedenkrát pro každý sloupec, což nám dává O(N2). Protože se ale může stát, že budeme procházet seznamem opakovaně, dokud se neumíme dostat do všech sloupců, potřebujeme zjistit, kolikrát nejvýše to uděláme.
Stačí se podívat na jedinou nabídku: 2 ·(N-1). Pokud budeme používat jenom tuto nabídku, tak se v případě lichého N po N krocích dostaneme do každého sloupce. Došli jsme tedy až do čísla N ·2 ·(N-1), a počet průchodů seznamem je tedy 2 ·(N-1) = O(N).
V případě sudého N se do lichých sloupců nedá dostat žádným způsobem a použitím stejné nabídky jako v předchozím případě se po N/2 krocích dostaneme do všech dostupných sloupců. Prošli jsme tedy seznamem opět O(N)-krát.
V obou případech tedy musíme projít v nejhorším případě O(N2) políček. Zpětný průchod pro zjištění výsledku projde každým sloupcem nejvýše jednou a složitost nám tedy nezhorší. Celková časová složitost tedy je O(N2 + N2 + N) =O(N2).
23-2-2 Zastavení (Zadání)
Zkusme nejprve generovat čísla 1 až 120. Hodíme jednou šestistěnkou a jednou dvacetistěnkou, máme tedy 6 možností, jak dopadne hod první kostkou a 20 možností, jak dopadne hod druhou kostkou. Celkem tedy máme 120 různých možností a pro každou možnost odpovíme jiným číslem.
Kdybychom chtěli generovat čísla od 1 do 50, hodíme dvakrát desetistěnkou a dostaneme 100 různých možných výsledků ((3,1) a (1,3) jsou rozdílné výsledky). Všechny výsledky jsou stejně pravděpodobné, každá kostka je dokonale náhodná a jednotlivé hody se neovlivňují.
Pokud tedy program odpoví jedničkou pro první dva výsledky (pro libovolné uspořádání), dvojkou pro další dva atd., umí správně generovat požadovaná čísla, protože generuje každé se stejnou pravděpodobností a potřebuje konečný počet hodů.
Nyní obecnější případ, chceme generovat N čísel a N dělí nějaký násobek počtů stěn našich kostek P – to je ve skutečnosti počet možných výsledků, které můžou nastat po hodech těmito kostkami. Rozdělíme všechny možné výsledky na N (disjunktních) částí o P/N prvcích a použijeme předchozí postup.
Zbývá ukázat, že pro jiná N nedokážeme na zaručeně konečný počet hodů vždy vygenerovat správný výsledek. Nejmenší N takové, že nedělí žádné možné P, je 7. V prvočíselném rozkladu žádného počtu stěn našich kostek totiž není 7.
Napřed rozeberme špatné postupy. Zahození některých výsledků – hodím osmistěnkou, pokud padne 8, hodím znova. Takovému algoritmu by mohla padat pořád 8 a nezastavil by se, leda by nám stačil průměrně konečný počet hodů, viz úloha 16-1-5
Když nemůžeme dostat vhodné P násobením, zkusíme sčítat – sečtu dvě padlá čísla po hodu čtyřstěnkou a od toho odečtu 1. Tento postup ale nedává stejné pravděpodobnosti všech čísel.
Jednička může vzniknout jen poté, co padne (1,1), ale trojka může vzniknout po pádu (1,3), (2,2) nebo (3,1), takže trojkou by algoritmus odpověděl s třikrát větší pravděpodobností. Některým číslem odpovím i jindy – pokud padne 8, odpovím jedničkou, ale toto triviálně nedává stejnou pravděpodobnost všem číslům.
Jak tedy dokázat, že žádný algoritmus si nemůže vystačit s konečným počtem hodů?
Pro spor budeme předpokládat, že existuje nějaký algoritmus, který správně generuje pro N, která nedělí žádné možné P. Po nějakém konečném počtu hodů program proběhne jedním z P různých způsobů (všechny jsou stejně pravděpodobné) a na konci každého odpoví nějakým z N požadovaných čísel.
Kdyby ale všechny odpovědi měly stejnou pravděpodobnost, znamenalo by to, že jsme dokázali P celočíselně a bez zbytku vydělit číslem N, což je spor s předpokladem.
Umíme tedy generovat jen pro taková N, která dělí nějaké P.
23-2-3 Projížďka (Zadání)
Trocha magie
Milý čtenář mi jistě pro jednou odpustí, pokud si zahraji na kouzelníka a vytáhnu jednoho králíka z klobouku.
Napřed, zadání šlo chápat různými způsoby, avšak příliš neměnilo podstatu řešení. Předpokládejme tedy například, že všechny cesty jsou jednosměrky a že „z rozcestí vychází sudý počet cest“ znamená, že právě polovina tohoto sudého počtu je v příchozím a právě polovina v odchozím směru.
 Opravdu nám stačí taková podmínka pro orientovaný graf. V neorientovaném
jsme potřebovali sudý počet, protože kdykoliv jsme vešli do vrcholu, také z něj
někudy musíme odejít. Stejně to funguje pro orientovaný, jen musíme přijít po
vstupní hraně a odejít po výstupní. Že jde o podmínku postačující, lze
nahlédnout také zcela stejně jako v neorientovaném grafu. Jediné, na co si
musíme dát pozor, je, že při vypisování dostáváme hrany pozpátku.
Opravdu nám stačí taková podmínka pro orientovaný graf. V neorientovaném
jsme potřebovali sudý počet, protože kdykoliv jsme vešli do vrcholu, také z něj
někudy musíme odejít. Stejně to funguje pro orientovaný, jen musíme přijít po
vstupní hraně a odejít po výstupní. Že jde o podmínku postačující, lze
nahlédnout také zcela stejně jako v neorientovaném grafu. Jediné, na co si
musíme dát pozor, je, že při vypisování dostáváme hrany pozpátku.
Na grafu na vstupu (rozcestí jsou vrcholy a cesty jsou hrany) si najdeme uzavřený eulerovský tah (to již za nás vyřešila kuchařka). Nyní jej projdeme a budeme si udržovat průběžný součet prošlých hran (říkejme tomu součtu odpočatost). Rozeberme dva případy.
Jako první případ vezmeme situaci, kdy po projití celého tahu dostaneme záporné číslo. Potom je součet všech hran záporný a takový zůstane, ať je vezmeme v libovolném pořadí. Proto úloha nemá řešení.
Pokud průšvih popsaný v minulém případu nenastane, vezmeme místo v tahu, kde se nachází minimum ze všech odpočatostí (místem v tahu není myšlen jen vrchol, ale i který průchod tímto vrcholem máme na mysli, neboť při různých průchodech můžeme mít různé hodnoty odpočatosti). V tomto místě v tahu začneme (jakoby jej pootočíme).
Složitost
Máme hezké lineární řešení (jak pamětí, tak časem), neboť již kuchařka nám ukázala, že eulerovský tah v dané složitosti zvládneme najít, a přidali jsme jen dva průchody vzniklým cyklem (jeden na průběžné počítání, druhý na výpis „pootočené“ verze).
Proč to funguje
Nyní už jen zbývá zdůvodnit, proč tento algoritmus vlastně počítá, co má. První případ je nezajímavý (neboť jsme jej již zdůvodnili výše). Dále tedy předpokládejme, že nám nastal druhý případ. Protože máme uzavřený eulerovský tah, projedeme každou cestou právě jednou. Zbývá dokázat, že odpočatost v pootočeném tahu nikde neklesne do záporných čísel.
Předpokládejme tedy, že v místě š na tahu máme zápornou odpočatost. Minimum máme v místě m. Pokud by v původním neotočeném tahu bylo š až za m, pak by muselo být také s menším číslem než m a m by tedy nebylo minimum. Tento případ tedy nenastal.
Takže š je před m. Představme si, že jsme prošli tahem dvakrát místo jednou, tedy při druhém průchodu š jsme na nižším čísle, než při prvním průchodu m (proto nám po pootočení v š vyšlo něco záporného). Ale protože druhý průchod nezačíná od nuly, ale od něčeho nezáporného, odpočatost druhého průchodu š je alespoň tak velká, jako první. Tedy i při prvním průchodu š jsme měli nižší číslo než u m, což je opět ve sporu s výběrem minima.
Jak na to přijít
Jednak, kdyby na to bylo jednoduché přijít, nebyla by úloha za 12 bodů. Ale přesto si řekneme způsob, jak na to přijít.
Můžeme si představit, že jsme řešení již našli a koukat na jeho vlastnosti. To, že je to uzavřený eulerovský tah, je vidět celkem jednoduše. Dále si všimneme, že vybráním jiného začátku se nám všechna čísla posouvají jen nahoru a dolů, rozdíly zůstávají stejné (s výjimkou rozpojeného konce – začátku). No a dále víme, že nejmenší číslo je 0 a to je na počátku.
23-2-4 Plánování (Zadání)
Budeme hladově přiřazovat letadla událostem tak, jak nám ze vstupu (seřazené dle počátků) přijdou pod ruku.
Podrobněji řečeno: v každé chvíli běhu programu si budeme udržovat hypotézu „stačí nám L letadel“, kde L navýšíme jen tehdy, ukáže-li se býti flagrantně špatná tím, že nebudeme mít při zpracování počátku události žádné volné letadlo.
Pokud volné letadlo mít budeme, prostě ho dané události přidělíme – k uchovávání volných letadel můžeme mít zásobník, do kterého budeme házet jejich pořadová čísla. Nebo frontu, pokud toužíme vytvářet zdání spravedlivého rozvrhování vůči pilotům. (Rozmyslete si.)
Tímto jistě dojdeme ke správnému minimu počtu letadel, protože pokud nám po poslední události zbyla hypotéza „stačí nám L letadel“, jistě se někdy stalo, že L-1 letadel nedokázalo pokrýt probíhající události. Zároveň je jasné, že tak umíme vytvořit správné rozvrhy, protože jsme si celou situaci de facto odsimulovali.
Z tohoto popisu to vypadá, že nám stačí lineární čas, ale celá věc má jeden háček: potřebujeme zpracovávat konce událostí (uvolňovat letadla), ale kdy?
Musí to být před dalšími odlety, abychom zbytečně nezvýšili L, musí to být po předchozích odletech, abychom nenabyli zdání, že letadel potřebujeme méně – asi nám nezbyde nic jiného, než tyto konce v O(N log N) zatřídit do vstupní posloupnosti, jejíž počáteční setřízení podle počátků nám nakonec z hlediska časové složitosti k ničemu nebylo.
Paměťová složitost je samozřejmě lineární.
Úloha souvisí se specifickými grafy, kterým se říká intervalové, ale jejich přímé použití by program nevyhnutelně zpomalilo a vzhledem k jednoduchosti algoritmu by nám nijak nepomohly ani ve výše provedené úvaze.
23-2-5 Zaměřování (Zadání)
Obsah trojúhelníku lze spočíst jako S = a va /2, kde a je základna a va odpovídající výška. Délka základny je známa, a tedy pokud existuje bod, který spolu s kanóny tvoří trojúhelník s obsahem právě S, bude ležet na průsečíku mnohoúhelníku a rovnoběžek spojnice kanónů ve vzdálenosti va od nich.
V programu si můžete všimnout, že jsou ignorovány hrany rovnoběžné se spojnicí kanónů. To si můžeme dovolit, neboť u nich záleží jen na okrajových bodech a ty se uváží nejpozději v kroku, kdy nenalezneme průsečík.
Pokud takový průsečík nenalezneme, tak bod, který by spolu s kanóny tvořil trojúhelník s obsahem právě S, neexistuje. Potom je třeba hledat bod, který spolu s kanóny vytvářel trojúhelník s obsahem co nejbližším k zadání. Jeden z takových bodů bude určitě vrchol mnohoúhelníku.
 To se snadno nahlédne sporem. Pokud by existoval takový bod X
uprostřed hrany AB, tak mohou nastat dvě možnosti. Buď je hrana AB
rovnoběžná se spojnicí kanónů (a pak je jedno, který bod z této hrany uvážíme
– všechny budou vytvářet trojúhelník se stejným obsahem), nebo není
rovnoběžná, a pak pokud s X hneme, tak na jednu stranu bude obsah
trojúhelníku růst, na druhou klesat. A jelikož víme, že trojúhelník s obsahem
přesně S neexistuje, tímto posunutím jsme našli bod s menším rozdílem obsahů
a máme spor.
To se snadno nahlédne sporem. Pokud by existoval takový bod X
uprostřed hrany AB, tak mohou nastat dvě možnosti. Buď je hrana AB
rovnoběžná se spojnicí kanónů (a pak je jedno, který bod z této hrany uvážíme
– všechny budou vytvářet trojúhelník se stejným obsahem), nebo není
rovnoběžná, a pak pokud s X hneme, tak na jednu stranu bude obsah
trojúhelníku růst, na druhou klesat. A jelikož víme, že trojúhelník s obsahem
přesně S neexistuje, tímto posunutím jsme našli bod s menším rozdílem obsahů
a máme spor.
Projdeme tedy všechny vrcholy mnohoúhelníku a najdeme ten, který odpovídá úloze.
Časová složitost je Θ(N) – seznam vrcholů projdeme právě 2× – a paměťová také Θ(N) – někde musí být uložen vstup. Pokud bychom uvážili, že vstup nám bude někdo zadávat postupně, dal by se program upravit, aby potřeboval jen další Θ(1) paměti.
 Následuje pár poznámek k užité analytické geometrii, kterou jsme hojně
využívali ve zdrojovém kódu.
Následuje pár poznámek k užité analytické geometrii, kterou jsme hojně
využívali ve zdrojovém kódu.
Skalární součin vektorů a→ a b→ se určí jako
Platí pro něj a→·b→ = |a→|·|b→|cosθ, kde θ je úhel, který spolu vektory a→ a b→ svírají a |a→|, resp. |b→| jsou velikosti vektorů a→ a b→. Speciálně platí √a→·a→ = |a→| a a→·b→ = 0, pokud jsou na sebe vektory a→ a b→ kolmé.
Dále potřebujeme popsat úsečku a přímku. Nejjednodušší je parametrický popis. Uvažme, že úsečka je mezi body, jejich polohu zapíšeme jako vektor od počátku souřadnic. Pro body X→ ležící na ní platí
kde t je reálný parametr nabývající hodnot mezi nulou a jedničkou. Zřejmě nula odpovídá bodu A→, jednička bodu B→ a ostatní hodnoty bodům mezi okraji. Pokud bychom z tohoto chtěli přímku, stačí vynechat omezení t ∈⟨0,1⟩.
Pro přímku však existuje i jiný způsob popisu. Uvažme, že známe vektor n→ kolmý na B→-A→. Pokud jím skalárně vynásobíme parametrický zápis přímky, dostaneme rovnici X→·n→ + c=0, kde c = -A→·n→ (tedy nějaká konstanta) a X→ obecný bod. Této rovnici se říká implicitní zápis přímky. Lze také ukázat, že každé řešení této rovnice je popsáno odpovídajícím parametrickým zápisem.
U implicitního zápisu ještě chvíli zůstaneme. Označme s→ vektor spojující body A a B, kterými prochází přímka, s→ = B→ - A→. Normálový vektor k němu zvolme n→ = (-sy,sx). Snadno nahlédneme, že opravdu n→·s→ = 0. Implicitní tvar rovnice přímky procházející body A a B tak může být zapsán jako n→·x→+c = 0.
Nyní však uvažme, co se stane, pokud do ní dosadíme bod, který na přímce neleží. Podívejme se podrobněji, co dostaneme na pravé straně. Bod X→ lze zapsat jako X→ = A→ + αn→ + βs→, kde α a β jsou nějaká jednoznačně určená čísla (α určuje posun po přímce od bodu A a β posun kolmo k ní). Po dosazení do implicitní rovnice dostaneme
Vzhledem k výše popsané konstrukci n→ si snadno čtenář ověří, že |n→| = |s→|, tedy že velikost normálového vektoru je rovna vzdálenosti bodů A a B. Kromě toho víme, že βn→ je takový posun směrem kolmým na přímku, abychom se z přímky dostali do bodu X. Tedy velikost tohoto vektoru (rovná |β|·|n→|) je výška trojúhelníku ABX kolmá na stranu AB.
Proto výraz |β|·|n→|2 popisuje dvojnásobek obsahu trojúhelníku ABX. Ten v programu budeme určovat vzorcem 2S = |X→·n→ + c|. Funguje jak pro určení obsahu trojúhelníku ABX, tak i pro určení rovnoběžky - zjevně stačí upravit konstantu c o ±2S.
Nakonec budeme potřebovat určit průsečík přímky a úsečky. Předpokládejme, že přímku máme implicitně zadanou ve tvaru n→·X→ + c=0 a úsečku mezi body P a Q zadanou parametricky X→ = P→ + t(Q→-P→). Dosazením těchto rovnic do sebe a vyjádřením t dostaneme
Pokud platí, že takto spočtené t ∈⟨0,1⟩, průsečík existuje, jinak ne.
23-2-6 Testovací (Zadání)
Nejjednduší řešení, které se nám na první pohled nabídne, je vyzkoušet všechny možné trojice (ai,aj,ak), pro které platí i < j < k, a pro každou takovou trojici otestovat, zda platí rovnost aj - ai = ak - aj. Tím získáme jednoduché řešení pracující v O(N3).
Jak si spousta z vás všimla, tento jednoduchý algoritmus můžeme urychlit tím, že využijeme setříděnosti posloupnosti a použijeme binární vyhledávání (o kterém se můžete dočíst v jedné z našich kuchařek). V naší úloze binární hledání využijeme k nalezení třetího prvku.
Tedy pro všechny dvojice (ai,aj) si spočítáme
a pokusíme se ak vyhledat v intervalu aj+1 až aN-1. Tím dostaneme řešení se složitostí O(N2 log N). Ale ani to ještě není optimálním řešením.
Optimální řešení pracuje v čase O(N2) a využívá jak setříděnosti posloupnosti, tak toho, že ke každé dvojici (ai, aj) existuje nejvýše jedno ak splňující podmínku. Jak na to?
Nejdříve si všimneme, že pokud ak0 - aj < aj - ai platí pro nějaké k0, tak tato nerovnost bude platit i pro všechna k < k0. Naopak pokud aj0 - ai < ak - aj0 platí pro nějaké j0, tak stejná nerovnost platí i pro všechna j < j0. Není těžké si na papíře rozmyset, proč.
A jak toho využijeme v našem řešení? Pro všechna možná i zvolíme j = i+1 a k = j+1 (následující prvky), pokud tedy i+2<N (musí existovat), a dále opakujeme následující postup.
Pokud aj - ai = ak - aj, nalezli jsme řešení, vypíšeme jej a k a j zvýšíme o jedna (pro jedno aj nemůže existovat více ak).
Pokud aj - ai > ak - aj, zvýšíme k o jedna. Je důležité si uvědomit, že tuto operaci můžeme udělat a nepřijdeme tak o žádné řešení, protože pro všechna nižší k řešení už také neexistuje, nebo jsme jej už vypsali.
Zbývá nám možnost aj - ai < ak - aj. V tomto případě zvýšíme j o jedna, protože pro tohle j už žádné řešení nebude.
Celý postup opakujeme, dokud k < n.
Nyní si jen stačí uvědomit, že u neklesající posloupnosti, kde můžou být bloky stejných čísel, se nám nic hrozného nestane – jen když po zvýšení nějakého indexu x ∈{i, j, k} zjistíme, že ax = ax-1, zvýšíme jej ještě jednou.
Složitost je O(N2), protože pro každé i maximálně N-krát iterujeme j i k o jedna. Toto řešení si můžete přečíst i jako zdrojový kód.
Nyní ještě dokážeme, že lepší časové složitosti v nejhorším případě nemůžeme dosáhnout. Uvažme jednoduše posloupnost 1, 2, …, N. V takové posloupnosti existuje N-2 trojic s diferencí 1, N-4 s diferencí 2, N-6 s diferencí 3 atd., až nakonec 1 trojice s diferencí (N-1)/3.
Počet všech trojic je tedy (N2-1)/4, což je vzhledem k N kvadraticky mnoho, takže algoritmus může mít až kvadraticky velký výstup a nemůžeme dosáhnout lepší složitosti v nejhorším případě než Θ(N2).
23-2-7 Regulomaty (Zadání)
Převeďte automat na obrázku na regulární výraz. To se drtivé většině z vás podařilo, strhával jsem body za chybějící vysvětlení.
(1+2+3+)* bylo správné řešení, někteří z vás zapomněli, že existuje
operátor + a zapsali to jako (11*22*33*)*, za což jsem strhával
řádově desetiny bodu.
Jak se ovšem úkol 1 řeší obecně? Jak dostanete z každého automatu regex, když jsem se v zadání chvástal, že to umím pro všechny? Existuje univerzální postup, který si tu předvedeme.
Postupně se budeme zbavovat vrcholů automatu, až nám jich zbyde jen pár, konkrétně ty vstupní a výstupní. Budeme na to pořád dokola používat tři operace:
- spojení paralelních hran
- odstranění smyček
- odstranění vrcholu
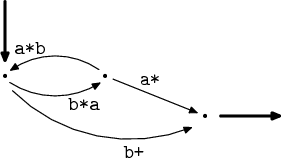
Celou věc si budeme ilustrovat na jiném, názornějším automatu, zde na obrázku.
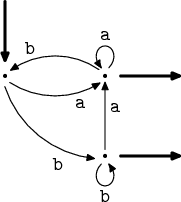
Před započetím ještě musíme automat upravit tak, aby měl jen jeden výstupní stav. K tomu použijeme ε-hrany, které si teď na chvíli povolíme.
Vytvoříme tedy jeden stav navíc, který bude oním jediným výstupním, a ze všech bývalých výstupních stavů do něj natáhneme ε-hrany.
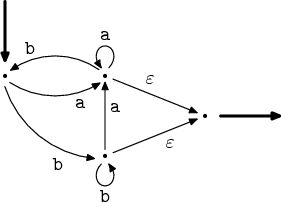
Nyní budeme cyklit pořád dokola naše tři body. Paralelní hrany zatím nemáme, ale smyčky se nějaké vyskytují, tak je zrušíme. Obalíme je hvězdičkou a připojíme na začátek výstupních hran. Teď už nebudou hrany označeny znakem, ale regexem. Nakonec zbydou dva stavy – vstupní a výstupní – a jediná hrana mezi nimi, která bude označena výsledným regexem.
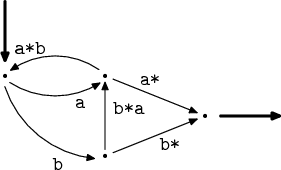
Vybereme si nějaký vrchol a ten odstraníme. Jednoduše vytvoříme všechny možné
kombinace hran, jež bylo možné použít, abychom prošli tímto vrcholem.
Samozřejmě neodstraňujeme vstupní a výstupní vrchol! Všimněte si, že na obrázku
už jsou spojené výrazy bb*a do b+a a bb* do b+.
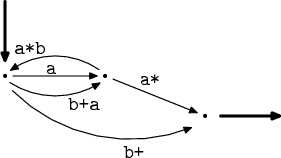
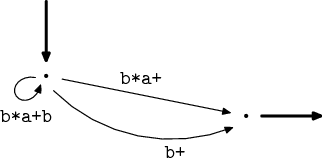
A zase od začátku. Spojení paralelních hran, tentokrát tady jeden případ máme,
tak pryč s nimi! Výrazy a a b+a se mi spojí do (a|b+a),
což můžeme upravovat postupně na (b+)?a a b*a, což je výsledný
výraz.
Eliminaci smyček pro tentokrát vynecháme, žádné v automatu zrovna nemáme, znovu budeme odstraňovat vrchol, teď už jediný odstranitelný.
Zase jsme mohli nově vzniklé výrazy zjednodušit. Z výrazu b*aa* máme
b*a+ a na smyčce z původního b*aa*b vznikl b*a+b.
Přichází na řadu spojení hran, při kterém vznikne ze dvojice výrazů b*a+
a b+ postupně (b+|b*a+), b*(b|a+) a b*[ab]a*.
Poslední přeměna už nebyla úplně mechanická – výrazu totiž odpovídá libovolný
řetězec nenulové délky, který nejdřív obsahuje jen b a potom jen
a.
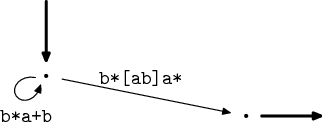
A po eliminaci smyček jsme u konce, na jediné hraně mezi vstupním a výstupním stavem máme výsledek.
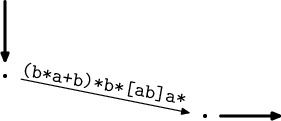
Správné řešení druhého úkolu bylo velice jednoduché, drtivá většina řešitelů za něj dostala plný počet bodů (s občasným stržením nějakých bodů za chybějící slovní popis, co že to je zač). Za nakreslení tohoto přehledného tvaru jsem uděloval malý bodový bonus.
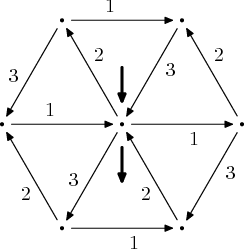
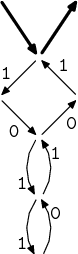
Uvedenému výrazu po krátkém zkoumání vyhovují všechny řetězce sestavené
z permutací 123, na obrázku jedničky symbolizují posun doprava, dvojky
vlevo dolů a trojky vlevo nahoru. Abych tedy po každém třetím znaku byl
v počátečním stavu, musím projít nějakou permutaci 123…
Poslední úkol nebyl tak jednoduchý na analýzu. Bylo potřeba aplikovat postup, který jsme si právě předvedli, jenže obráceně. Víc asi napoví obrazový materiál.
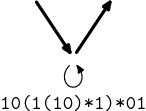 →
→ 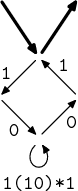 →
→ 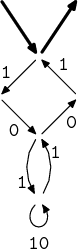 →
→ 
Postup je tedy jednoduchý. Hvězdičku rozbalím na cyklus, znaky ze začátku a
konce výrazu převedu na samostatné hrany. Více hvězdičkovaných výrazů oddělím
ε-hranou. Kdyby se objevilo více možností, udělám z nich paralelní
hrany. Předvedu ještě na příkladu [13]*2*(11|3):
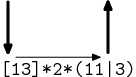 →
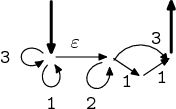
→ 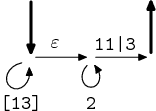 →
→ 
Nejasnosti a upřesnění řeším standardně na fóru, nebojte se zeptat. Můžete si také stáhnout zdrojové kódy obrázků (Metapost).