Pátá série dvacátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 23-5-1: Boj s nanoboty
- 23-5-2: Zjednodušení situace
- 23-5-3: Hra pro jednoho hráče
- 23-5-4: Model čtoucího řidiče
- 23-5-5: Kuchařková
- 23-5-6: Předposlední
- 23-5-7: Perlím, Perlíš, Perlíme
23-5-1 Boj s nanoboty (Zadání)
Napřed si představíme jednodušší řešení. Podívejme se na problém jako na trojrozměrný svět (dva prostorové rozměry a jeden čas). Nebo pokud nemáte časoprostorovou představivost, zkuste si představit hromadu 2D-světů nad sebou (dole je v čase 0, nad ním v čase 1 atd.).
A v těchto světech budeme ukládat, na která všechna políčka se hrdina mohl dostat a kolik živých lidí již mohl mít na svědomí, pokud by nyní pobýval na tomto políčku. Tedy v nultém světě (v tom přímo zadaném) se může nacházet pouze na jednom políčku ((0,0)) a nemá na kontě nikoho (předpokládejme, že padouch začíná hrát nejdříve v čase 1).
Jak spočítáme novější verzi našeho světa? Z každého políčka, kde se mohl nacházet, ho zkopírujeme do stejného a všech sousedních políček. Je-li na nově obsazeném políčku zrovna na potvoru padouch, tak ho zamorduje a my si přičteme skóre.
Pokud máme možnost nakopírovat hrdinu z více políček, samozřejmě si vybereme to s nejlepším skóre (to, jak se dostal na toto políčko, již neovlivní budoucnost a záchranou více lidí si celkově pomůže, nikdy si nemůže uškodit).
Ke zrekonstruování výsledku si ke každému možnému výskytu hrdiny také potřebujeme poznamenat, které bitvy s padouchem se účastnil předtím.
Po spočítání všech pater stačí jen najít výskyt s nejvyšším skóre a prohrabat se zpětně bitvami, které podstoupil.
Toto by samozřejmě fungovalo, ale je to pomalé. Můžeme si ale všimnout, že většinu času trávíme sledováním bloumání hrdiny po okolí. Nás však zajímá, jen jestli se včas dostaví na rande, ne kterou cestu k tomu zvolil. Taktéž, není zajímavé, kde tráví přebytečný čas (čekat může kdekoliv).
Takže se omezíme pouze na zajímavé události. Všimněme si také, že pro zjištění, jak dlouho bude cesta trvat, stačí jen sečíst vzdálenosti míst v obou souřadnicích, tedy pokud jsou sousední jen do stran, nahoru a dolů. Kdybychom uvažovali i diagonální sousedy, pak by to bylo maximum z těchto vzdáleností.
Tak tedy, seřaďme si vypuštění nanobotů chronologicky, od nejbližšího v budoucnosti po nejvzdálenější. Pro každou událost se podíváme, ze kterých všech střetů se to sem dá stihnout. Z nich vybereme ten, který má nejlepší skóre, a uložíme si jej.
Pro jednoduchost považujme narození hrdiny také za střet. Nakonec vybereme událost, po které měl největší skóre, a stejným způsobem jako v předchozím řešení ji odmotáme k začátku.
Složitosti jsou jednoduché – pamatujeme si všechny události, tedy paměťová je lineární. A pro každou událost si prohlížíme všechny předchozí, což je 1+2+3+…+n, z čehož nám vyjde složitost kvadratická.
A proč to vlastně funguje? Využíváme pozorování zmíněné v prvním řešení – že pokud se už hrdina někde vyskytuje, tak na budoucnost již nemá vliv, jak se tam dostal, proto je pro nás nejvýhodnější, aby se na takovém místě vyskytoval s nejvyšším možným skóre.
Z toho indukcí dokážeme, že po každé události by měl maximální možné skóre, kdyby se jí účastnil. U narození je to jasné a u každé další to odvodíme z toho, že jsme si vybrali tu nejlepší předchozí událost.
23-5-2 Zjednodušení situace (Zadání)
Tuto úlohu – dělení množin bodů jednou přímkou na poloviny – bylo těžké nejen vyřešit, ale také zadat do CodExu.
Stojí za zmínku, že v mnoha (i náhodných) případech se dá použít rozumných heuristik (setřídit podle nějaké osy, zkusit najít řešení, případně zvolit jinou osu a iterovat) a řešení je pak stejně rychlé jako varianta optimálního řešení.
Děkujeme všem, kteři upozornili na tuto slabinu původního zadání.
Klíčové pozorování k řešení naší úlohy je, že si vlastně můžeme představit, že ona oddělující přímka prochází dvěma body vstupu – pokud bychom našli nějakou, která toto nesplňuje, můžeme ji nejdřív posunout a pak pootočit tak, aby již tento invariant splňovala.
Obtíž máme jen s tím, že zadání příkladu tuto situaci zakazuje – vyřešíme to tedy tak, že najdeme řešení s body na dělící přímce a pak jen přímku o kousek pootočíme správným směrem a posuneme.
Určitě umíme vyřešit problém v čase O(n3) – pro každou dvojici bodů ze zadání existuje právě jedna přímka, která jimi prochází, a pro tuto přímku v lineárním čase snadno zkontrolujeme, je-li to ta hledaná, či nikoli.
Pro řešení v lepším čase než kubickém použijeme klasický geometrický trik – kubické řešení často zahazuje mezivýsledky, avšak my si pro nějakou množinu bodů umíme existenci řešení najít rychleji než pro každý zvlášť. Nejen v tomto případě budeme hledat všechny možné dělící přimky, které prochází jedním bodem.
Vezmeme si bod a setřídíme si okolní body podle směrnice. Představit si to můžeme tak, že máme náš bod uprostřed a kolem něj točíme postupně onu dělící přímku.
Pak procházejme ostatní body podle pořadí, které nám určilo setřídění. Pro první bod si spočítáme počet vojáků na obou stranách klasicky, v lineárním čase. Každý další bod už ale umíme zpracovat v konstantním čase – vždy přechází buďto „zprava doleva“, nebo „zleva doprava“ a podle toho přičteme a odečteme jedničku.
Takto umíme v čase O(n log n) zkontrolovat všechny přímky, které mají jeden společný bod. Protože už víme, že naše hledané řešení obsahuje dva body ze vstupu, musíme po lineárním počtu kroků najít správné řešení. Časově jsme se dostali na O(n2 log n) a paměťově na O(n).
Pro úplnost vzorového řešení se ujistíme, že přímku lze vždy správně posunout, tedy že nejbližší celočíselný bod je od ní dostatečně daleko.
Mějme tedy přímku určenou dvěma body, můžeme předpokládat, že není vodorovná ani svislá, pro ně to platí jistě. Jeden z bodů si můžeme (posunutím osy) zadefinovat jako (0,0), ten druhý jako (k,l). Navíc o souřadnicích (k,l) můžeme tvrdit, že jsou nesoudělné, jinak bychom bez újmy na obecnosti volili jiný bod.
Představme si nyní naši přímku jako graf funkce k ·x/l. Vkládejme za x celá čísla, dostáváme hodnoty y-ové souřadnice. Pokud výsledek nebude celé číslo, jak daleko může být? Alespoň 1/l, protože neumíme zvýšit jmenovatel. Pokud bychom otočili osy, získali bychom, že to musí být alespoň 1/k.
Toto však není úplně přesné. Máme pravoúhlý trojúhelník, jehož odvěsny jsou dlouhé alespoň 1/k a 1/l. Spočítáme-li nyní jeho přeponu Pythagorovou větou a následně výšku na přeponu z vzorce S=ab=cvc, získáváme skutečnou vzdálenost mřížového bodu od přímky.
| √2 |
| 200 000 |
Zbývá otázka – je to optimální řešení? Ale kdepak! Tato úloha je celkem slavná, je to konkrétní varianta problému sendviče se šunkou, anglicky Ham sandwich problem.
Pro náš rovinný případ jej lze řešit dokonce v lineárním čase, můžeme jej řešit dokonce i ve více dimenzích (tam bychom pak hledali nadroviny). Optimální řešení využívá principu „Rozděl a panuj“ tak, že v každem kroku vyhodí lineárně mnoho kandidátů na dělící přímku a pokračuje dále.
Algoritmus je to však poněkud netriviální a pracuje s duální verzí problému (tedy hledá bod, který leží nad i pod právě polovinou přímek), takže jej tady neuvádíme. Možná se k němu dostaneme někdy příště.
Jste-li netrpěliví, můžete si oprášit angličtinu a najít si odborný článek „Algorithms for Ham-Sandwich Cuts“ od autorů Lo, Matoušek a Steiger. Nepodaří-li se vám jej získat, napište nám, zařídíme.
23-5-3 Hra pro jednoho hráče (Zadání)
Hanojské věže jsou klasickým příkladem na rekurzi. Máme dané kotouče n…1, n ≥ 2 a chceme je přesunout z tyče A na tyč C za pomoci tyče B. Postup vypadá takto:
- kotouče (n-1)…1 přesuneme z tyče A na tyč B,
- nic nám teď nebrání přesunout kotouč n z tyče A na tyč C,
- kotouče (n-1)…1 z tyče B položíme na tyč C.
Programem to samé počítači vysvětlíme skoro stejně:
def hanoj(n, zdroj, pom, cil):
if n != 1:
hanoj(n-1, zdroj, cil, pom)
print(str(n) + ": " + zdroj + "->" + cil)
if n != 1:
hanoj(n-1, pom, zdroj, cil)
hanoj(3, "A", "B", "C")
Časová složitost je exponenciální vůči n a lineární vzhledem k velikosti výstupu, což je to nejlepší, v co jsme mohli doufat. Pokynů k přesunu kotouče bude 2n-1 – to lze z algoritmu dokázat indukcí, vždyť 2(2n-1-1)+1=2n-1.
Kód si pro řešení našeho zadání můžeme docela snadno upravit tak, aby sledoval stav hry a odpočítával tahy. Až zjistíme, že jsme v kýženém tahu, prostě jen stav vytiskneme.
def hanoj(n, zdroj, pom, cil, k, kyzeneK, stav):
if n != 1 and kyzeneK < k + 2**(n-1) - 1:
hanoj(n-1, zdroj, cil, pom, k, kyzeneK, stav)
k += 2**(n-1) - 1
if k == kyzeneK: print(stav)
stav[cil].append(stav[zdroj].pop())
k += 1
if n != 1 and kyzeneK > k - 1:
hanoj(n-1, pom, zdroj, cil, k, kyzeneK, stav)
Algoritmus funguje, ale má stále časovou složitost O(2n), přičemž v tomto případě to už výstupem neomluvíme – ten je lineární.
Lineární algoritmus existuje – stačí si uvědomit, že při rekurzivním
procházení nikdy nepotřebujeme volat funkci hanoj dvakrát. Když totiž
přesně víme, kolik tahů které volání udělá, umíme určit, jestli se k-tá
pozice vyskytuje až po přesunu kotouče, nebo ještě před ním.
Pak už si jen zjednodušíme práci tím, že stav hry nebudeme udržovat, ale budeme ho rovnou průběžně tisknout. Zde je výsledný algoritmus řešící problém v lineárním čase i prostoru.
def hanoj(n, zdroj, pom, cil, k, kyzeneK):
if n == 0 : return
if kyzeneK < k + 2**(n-1) :
print(str(n) + " je na tyci " + zdroj)
hanoj(n-1, zdroj, cil, pom, k, kyzeneK)
if kyzeneK >= k + 2**(n-1) :
print(str(n) + " je na tyci " + cil)
hanoj(n-1, pom, zdroj, cil, k + 2**(n-1), kyzeneK)
hanoj(3, "A", "B", "C", 0, 3)
Rozmyslete si, nečiní-li nám problém užití pythonovského mocnění. Má program, jak je napsán, opravdu lineární složitost? Pokud ne, proč? Bylo by těžké to opravit? Další námět k zamyšlení – paměťová náročnost algoritmu, jak je implementován, je lineární. Jak ji srazit na konstantní?
Víceméně toho samého programu se šlo dobrat i zapřemýšlením nad tím, co má náš problém společného s počítáním n-té permutace.
Velká část řešitelů naměřila, že výraz
| M |
| 2N |
| 1 |
| 2 |
při vhodném nastavení znaménka a zaokrouhlení (podle N) dává kýžené číslo tyče pro N-tý disk; M pak určuje číslo tahu. S různým úspěchem se řešitelé snažili tuto skutečnost využít ve svém řešení, leč kamenem úrazu byla absence důkazu správnosti a časté drobné chyby.
Několik řešitelů používalo poznatek z Wikipedie o vztahu dvojkového zápisu čísla tahu a situace hry. Nic jsem proti tomu neměl, pokud autor prokázal kvalitním zdůvodněním, že rozumí, co se v postupu děje.
23-5-4 Model čtoucího řidiče (Zadání)
Priamo zo zadania vyplýva, že pre každú hranu, ktorou na križovatku prídeme, je jasne určená hrana, ktorou zase odídeme. Naopak, pre jednu výstupnú hranu môže byť viacero vstupných.
Na začiatku si očíslujeme hrany a z pôvodného grafu zostrojíme štruktúru, v ktorej budeme hľadať cesty. Táto štuktúra bude reprezentovaná ako pole hrán, kde každá hrana si pamätá svojho následovníka, a zoznam svojich predchodcov.
Štruktúru vytvoríme v čase O(M). Pre každý vrchol v pôvodnom grafe postupne prechádzame zoznam jeho hrán odzadu. Ak narazíme na výstupnú hranu, poznamenáme si ju ako hranu H. Ak narazíme na vstupnú hranu, nastavíme jej následovníka hranu H, a hrane H pridáme do zoznamu predchodcov spracovávanú vstupnú hranu.
Je zaujímavé si uvedomiť, že kým skoro každá hrana má nutne následovníka (okrem hrán vedúcich do vrcholu bez výstupných hrán), viacero hrán môže nemať predchodcu. Napríklad ak má vrchol tri výstupné hrany za sebou, na druhú a tretiu sa šofér nikdy z iného vrcholu nedostane. Ale môže nimi svoju cestu začať.
Po vytvorení štruktúry nastavíme každej hrane príznak, že ešte nebola spracovaná. Hrana si tiež pamätá, aký vrchol je jej začiatočný a aký je koncový (keďže je orientovaná).
Teraz začneme hľadať cesty. Na začiatku si vezmeme prvú hranu a prechádzaním dopredu si vytvárame spojový zoznam hrán tejto cesty. Keďže v pôvodnom grafe hľadáme cestu s N vrcholmi, a teda N-1 hranami, v našej štruktúre hrán to odpovedá ceste dĺžky N-1.
Cesta je teda reprezentovaná spojovým zoznamom hrán, ktoré používa, a držíme si ukazateľ na jej začiatok a koniec.
Vrcholy, ktorými cesta prechádza, si pamätáme pomocou poľa o veľkosti N, kde hodnota v poli na mieste i vyjadruje, koľkokrát daná cesta prechádza vrcholom i. Okrem toho si tiež musíme pamätať, koľko rôznych vrcholov sme navštívili.
Pri vytváraní cesty si vždy pri pridaní hrany zvýšime hodnotu v poli navštívených vrcholov. Dôležité je, že ak sa hodnota zmenila z 0 na 1, zvýšime počet rozdielnych navštívených vrcholov.
Po pridaní hrany si túto hranu označíme ako spracovanú. Takisto pridám jej cenu do celkovej ceny cesty.
Po vytvorení cesty skontrolujeme, koľko rôznych vrcholov sme navštívili. Ak ich je N a cena cesty je lepšia ako doteraz najlepšia nájdená, uložíme si cestu ako najlepšiu doteraz nájdenú. Keďže cesta je jednoznačne určená svojou začínajúcou hranou, stačí si uložiť len prvú hranu cesty.
Takže máme nájdenú nejakú prvú cestu. Je dôležité si uvedomiť, že táto cesta nemusí mať práve N-1 vrcholov. Mohla skončiť predčasne, ak jej koncová hrana už nemala následovníka. To však nevadí, ako uvidíme neskôr. Teraz pomocou tejto cesty nájdeme ďalšie cesty, a to prehľadávaním do hĺbky.
V každom kroku sa najprv pozrieme, či má začiatočná hrana cesty nejakého predchodcu, po ktorom sme sa ešte nevracali (berieme ich postupne v tom poradí, ako ich máme uložených).
Ak áno, posunieme cestu o jeden vrchol dozadu – pridáme predchodcu súčasnej začiatočnej hrany na začiatok cesty, pridáme hodnotu tejto hrany do celkovej ceny cesty, a zvýšime čítač v poli navštívených vrcholov u začiatočného vrcholu práve pridanej hrany. Taktiež upravíme hodnotu, koľko rôznych vrcholov sme navštívili (ak sa nám zmenila 0 na 1).
Ak je cesta dlhá N-1 hrán (čo nie je vždy, môže byť aj kratšia), zrušíme poslednú hranu na konci (na ktorú si držíme ukazateľ). Odčítame jej hodnotu z celkovej hodnoty cesty.
Tiež znížime čítač v poli navštívených vrcholov u koncového vrcholu hrany. Ak sa nám zmenila hodnota z 1 na 0, znížime počet rôznych vrcholov, ktoré sme navštívili. Ak je cesta kratšia ako N-1, koncovú hranu necháme, čím cestu o jedna predĺžime.
Naopak, pokiaľ sa cesta nemôže posunúť smerom dozadu, pokúsime sa ju posunúť smerom dopredu – posunieme začiatočnú hranu na jej následovníka, pričom upravíme počty navštívených vrcholov. Ak má koncová hrana následovníka, posunieme aj ju. Ak nemá, koniec neposúvame, a cesta sa nám proste skráti.
Pri posune dopredu si musíme dať pozor na cykly, po ktorých by sa cesta mohla posúvať teoreticky donekonečna.
Po posune cesty si také nové hrany, cez ktoré prejdeme, poznačíme ako spracované.
Na konci posunu sa pozrieme, koľko rôznych vrcholov sme navštívili. Ak je ich práve N a cena cesty je lepšia ako doteraz najlepšia, upravíme hodnotu najlepšej doteraz nájdenej cesty (konkrétne len začiatočnej hrany cesty) a jej cenu.
Ak sa nie je kam pohnúť, tak sme skončili spracovanie jedného súvislého úseku hrán. Úsekov ale môže byť viacero. Takže nájdeme úvodnú cestu v novom úseku.
To urobíme tak, že v zozname hrán nájdeme ešte nespracovanú hranu a z nej spustíme hľadanie úvodnej cesty. Zoznam však neprechádzame od začiatku, ale od miesta, kde sme skončili posledne, preto je zložitosť nájdenia všetkých začiatkov O(M).
Analýza celkovej zložitosti je následovná – vstup načítame v zložitosti O(M+N). Následovníkov a predchodcov hrán spočítame v O(M). Nájdenie všetkých začiatkov ciest je dokopy tiež O(M). Ostáva spočítať zložitosť hľadania ciest.
Posun cesty zvládneme v čase O(1). Koľko takýchto posunov bude? Keďže následovník každej hrany je maximálne jeden, je každá hrana predchodcom pre najviac jednu hranu. Celkový počet predchodcov je teda maximálne M.
Pri pohybe dozadu sa každá hrana vyskytne na začiatku cesty práve raz, pričom poradie určuje prechádzanie do hĺbky. Pohyb dopredu je jednoznačne určený pohybom dozadu – dopredu sa hýbeme len keď sa nedá hýbať dozadu, čím simulujem práve prehľadávanie do hĺbky.
Keď si to predstavíme, vidíme, že pri pohybe dopredu sa začiatok vracia po hranách, ktorými predtým prešiel dozadu. Každou hranou teda prejde maximálne dvakrát – raz dopredu a raz dozadu. Pri koncových hranách úseku je možné, že nimi prejde len raz, a to dopredu.
Keďže jeden posun cesty zaberie O(1), celková zložitosť nájdenia všetkých ciest bude O(M).
Časová zložitosť algoritmu je teda O(M+N), pamäťová tiež O(M+N).
Väčšina riešiteľov úlohu vyriešila v čase O(MN). Táto jednoduchšia varianta spočíva v tom, že postupne berieme všetky hrany ako začiatky ciest a sledujeme, či cesta dlhá N vrcholov prechádza všetkými vrcholmi.
Pritom však nesmieme zabudnúť na to, že si následovníkov hrán treba predpočítať dopredu, aby sme ich dokázali určiť v konštantnom čase. Ak by sme pre nájdenie následovníka hrany zakaždým museli prechádzať celý zoznam hrán vo vrchole, časová zložitosť nám narastie na O(M2).
Skonštruujeme si graf následovne. Na začiatku pridáme hrany tak, aby vznikla Hamiltonovská kružnica. Označme si tieto hrany „tučne“. V každom vrchole je teraz jedna vstupná a jedna výstupná hrana.
Medzi tieto hrany teraz v smere jazdy šoféra vložíme (M-N)/2N vstupných hrán, a v opačnom smere (M-N)/2N výstupných. Teraz je teda pôvodná tučná výstupná hrana následovník pre všetky nové vstupné hrany, a naopak, práve vložené výstupné hrany nemajú predchodcu.
Druhé konce vložených hrán zvolíme tak, aby vznikol korektný graf.
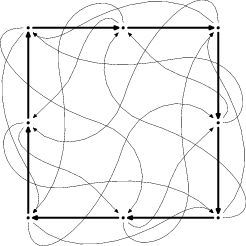
Analýza zložitosti hľadania ciest v tomto grafe je následovná. Pre každú hranu platí, že môže byť na ceste prvá až N-tá. Tučná hrana bude raz prvá a M/2N-krát druhá až N-tá, teda pre ňu budeme hľadať následovníka dokopy O(M)-krát.
Nájdenie následovníka pre tučnú hranu trvá O(M/N) (musíme prejsť všetky umelo pridané vstupné hrany medzi ňou a výstupnou hranou). Takže na každej tučnej hrane spotrebujeme dokopy O(M2/N) času.
Tučných hrán je O(N), teda na všetkých tučných hranách spotrebujeme celkovo O(M2) času. Novopridané hrany už výsledok neovplyvnia.
23-5-5 Kuchařková (Zadání)
Našim úkolem je dokázat, že úloha Metr je NP-úplná. Jak nám kuchařka radila, je příliš pracné dokazovat úplnost tak, že převedeme na Metr všechny úlohy z NP. Raději tedy dokážeme, že lze jednu NP-úplnou úlohu vyřešit pomocí Metru.
Nejtěžší v NP-úplnostních převodech bývá rozpoznat, která úloha se nám bude převádět nejsnáz.
Na Metru stojí za všimnutí, že překládání samotného metru do pouzdra nám v jistém smyslu rozděluje úseky na dva typy – pokud jde metr uložit, tak jeden typ úseku je přeložen na jednu stranu (řekněme zprava doleva) a druhý je přeložený nazpátek (zleva doprava). Navíc je metr zadán jako posloupnost čísel.
Když se podíváme do seznamu NP-úplných úloh, najdeme tam úlohu Dva loupežníci, která také rozděluje čísla na dvě hromádky. Zkusme tedy pomocí Metru řešit Loupežníky.
Připomeňme si zadání Dvou loupežníků z kuchařky:
Název problému: Dva loupežníci
Vstup: Seznam nezáporných celých čísel.
Problém: Existuje rozdělení seznamu na dvě hromádky tak, že každé číslo bude v právě jedné hromádce a v každé hromádce bude stejný součet čísel?
Začněme tedy převádět vstup Dvou loupežníků na vstup Metru. Vstup Loupežníků nám nijak neurčuje, jak velké má být pouzdro metru – to si tedy můžeme zvolit sami, aby se nám snáz převádělo.
Dopředu není úplně jasné, jaká velikost by se nám hodila. Bude nám stačit součet všech předmětů (označujme ho σ), nebo velikost jednoho lupu, σ/2? Méně než σ/2 nedává příliš smysl, ale více by mohlo…
Jak jsme diskutovali výše, mohlo by nám stačit označit ty části metru (tedy tu část kořisti), které jdou zleva doprava, jako lup pro loupežníka A a ty, které jdou zprava doleva, přiřadíme loupežníku B.
Nyní se zamysleme nad vstupy, které by nám mohly dělat neplechu. Například
seznam předmětů 1 1 1 by se do pouzdra velikosti alespoň 1.5 snadno
vešel, ale my musíme odpovědět NE, protože jej rozdělit pro dva
loupežníky nelze.
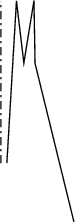
Mohli bychom tedy zkusit nastavit, aby začátek i konec lupu končil ve stejném bodě metru – například tak, že na začátek i konec přidáme úsek dlouhý jako celé pouzdro.
Tím by určitě odpadl případ 1 1 1. Jak by taková úprava
vstupu vypadala, vidíte na obrázku. Bohužel nám po chvíli úvah
dojde, že by nám také odpadl případ 1 3 1 1, který ovšem rozdělit jde.
Podívejme se na vstup 1 3 1 1 a zamysleme se, jak naši úvahu vylepšit.
Na dalším obrázku jsme jej zakreslili tak, aby se uložení metru podobalo grafu
funkce, který začíná a končí v nule.
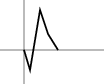
Každé rozdělitelné zadání Dvou loupežníků jde takto nakreslit – prostě jednu část kresleme jako rostoucí úsečky a druhou jako klesající.
Můžeme tedy vhodnou úpravou našeho vstupu pro Loupežníky zajistit, aby řešení Metru přesně odpovídalo grafu takovéto funkce?
Ano, stačí jen trochu upravit nápad, který jsme měli před pár odstavci. Potřebujeme totiž v Metru povolit, abychom mohli vstoupit na grafu i do „záporných hodnot“.
Na začátek metru tedy vložme úsek o velikosti k, což bude také velikost pouzdra. Ten se dá do pouzdra vložit jen tak, že jeho konec bude na okraji pouzdra. Další úsek si tedy také zvolme – tentokrát jako k/2. Z okraje pouzdra jsme se tedy dostali přesně doprostřed. To bude náš počátek grafu.
Dále už pokládejme úseky o velikosti stejné, jako byly hodnoty na vstupu Dvou loupežníků, a ve stejném pořadí. Abychom se ujistili, že na konci opravdu naše funkce skončí v nule, přidejme ještě jeden úsek délky k/2 a za něj úsek délky k.

Nyní už víme, co od k chceme – abychom neřekli zbytečné ne, pokud bychom neměli dostatečný rozsah na jejich poskládání. Bude nám stačit nastavit k=σ, ale klidně bychom mohli mít pouzdro i větší.
Převod je dokonán, pojďme si tedy ukázat, že je korektní.
Už během rozboru jsme si rozmysleli, že řešení Dvou loupežníků existuje právě tehdy, když existuje nakreslení lupu jako grafu funkce tak, že graf začíná i končí v nule.
V naší konstrukci platí, že metr lze vložit právě tehdy, když část odpovídající lupu loupežníků začíná a končí uprostřed pouzdra – a to platí právě tehdy, když existuje onen graf funkce začínající a končící v počátku.
Složením těchto ekvivalencí dostaneme, že náš převod odpoví ano na Metr právě tehdy, když problém Dva loupežníci šel vyřešit, a tedy je vše v pořádku – Metr je NP-těžký.
Pro formální správnost si ještě povězme, že rozdělení metru (informace o tom, kde metr začíná a v jakém směru jej zlomit) je polynomiálně velkým certifikátem k našemu problému, a Metr je tedy v NP. Obě tvrzení spojíme dohromady a dostáváme, že Metr je NP-úplný.
23-5-6 Předposlední (Zadání)
Největší problém celé úlohy je poznat, že se jedná o toky v sítích (něco o tocích si můžete přečíst v kuchařce ke 4. sérii). My si nyní tipneme, že se jedná o nějaký tok, a budeme se jej tam snažit najít. Jak na to?
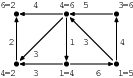
Vstupní hrany a výstupní hrany jsou na sobě nezávislé v rámci vrcholu. Tak si každý vrchol rozdělíme na 2 nové vrcholy, levý a pravý.
Levý nám bude reprezentovat výstupní část (z této části povedou všechny hrany) a pravý bude reprezentovat vstupní část (do tohoto vrcholu naopak povedou všechny hrany).
Není těžké nahlédnout, že jsme takto vytvořili orientovaný bipartitní graf, kde všechny hrany vedou z levé partity do pravé.
Nyní ještě potřebujeme zohlednit maximální vstupní součet a minimální výstupní součet. To uděláme tak, že do grafu přidáme další 2 vrcholy.
Jeden pojmenujeme zdroj a povede z něj hrana do každého vrcholu levé partity. Tyto hrany budou ohodnoceny maximálním výstupním součtem příslušných vrcholů.
Druhý pojmenujeme stok a z každého vrcholu pravé partity do něj povede hrana. Tyto hrany budou ohodnoceny minimálním vstupním součtem příslušných vrcholů.
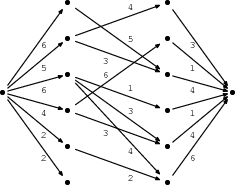
Nyní máme ohodnocený orientovaný graf se zdrojem, stokem a celočíselnými kapacitami hran. Zavoláme tedy některý z algoritmů na hledání maximálního (celočíselného) toku, například Fordův-Fulkersonův algoritmus s hledáním zlepšujících cest pomocí prohledávání do šířky (viz kuchařku).
Pokud se velikost maximálního toku bude rovnat sumě minimálních výstupních součtů, tak jsme našli příslušné ohodnocení. Pokud ne, tak neexistuje žádné řešení.
Proč to funguje? Hrany ze zdroje do levé partity nám zajišťují, že se do grafu nikdy nedostanou takové hrany, které by porušovaly podmínku maximálního výstupního součtu. Hrany mezi partitami jsou přesně ty samé hrany jako hrany v původním grafu.
Hrany vedoucí z pravé partity do stoku nám obstarávají minimální vstupní součty a jejich kapacity jsou právě tyto hodnoty. Kdybychom totiž měli řešení, ve kterém by některý vstupní součet byl větší než daný minimální, tak pak můžeme tok hran vedoucích dovnitř libovolně snížit tak, aby jejich součet byl roven minimálnímu vstupnímu součtu a všechny podmínky zůstanou zachovány.
Hrany z pravé partity do stoku nám tvoří v grafu řez. Problém má řešení, právě když tyto hrany jsou naplněny na maximum. Hrany mezi partitami nám také tvoří řez, takže vše, co proteče ze zdroje do stoku, proteče i hranami mezi partitami. A hrany mezi partitami reprezentují hrany původního grafu, takže tok na nich je naším řešením.
Nyní k časové složitosti. Časová složitost převodu na nový graf je O(n+m), kde n je počet vrcholů v původním grafu a m je počet hran.
Každý vrchol zdvojíme, na každou hranu se podíváme jen jednou a přidáváme jen 2 nové vrcholy a s nimi dohromady 2n hran. Zbytek časové složitosti závisí na použitém algoritmu pro zjištění maximálního toku. V našem případě, kdy jsme použili Forda-Fulkersona s procházením do šířky, je to O(nm2).
23-5-7 Perlím, Perlíš, Perlíme (Zadání)
V úloze byly zadány dva úkoly. První těžší, druhý lehčí. S oběma jste se dokázali velmi dobře vyrovnat.
První úkol bylo možno řešit dvěma způsoby. Buďto smažu menší ze zadaných čísel, nebo matchnu celý výraz a správnou konstrukcí z backreferencí vyberu to větší. Oba postupy využívaly rekurzi a rozhlížení (bez toho to pravděpodobně nešlo).
Mnoho z vás si všimlo, že z rozhlížecích předpokladů se dá sestavit jakási
podmínka – ((?=A)B|C) znamená jednoduše to, že pokud řetězec splňuje
regex A, tak použij B, jinak použij C.
Rozeberme si autorské řešení. Předpokládáme v něm, že čísla nejsou uvozena nulami.
s#^((?=(.((?2)| ).).+).* (.*)|(?=.+(?2)(?!.))(.*) .*|(.*)0.* (\6[1].*)|((.*)1.*) \9[0].*)$#$4$5$7$8#
Na prvním řádku jsme rekurzí zjistili, že druhé z čísel je delší, takže si vybereme to druhé z nich. Na druhém řádkujsme analogicky zjistili, že první
z čísel je delší. Mimochodem, domácí cvičení – jaký je rozdíl mezi (?!.) a $?
Na třetím řádku jsou tedy čísla nutně stejně dlouhá. Využijeme žravosti
hvězdičky (.* polkne co nejvíc) a předloženým výrazem zjistíme rozdíl
dvou stejně dlouhých čísel – porovnáváme první cifru, která se liší.
Na posledním řádku je nahrazovací výraz. Jsou to reference na „ty správné závorky“, které buďto nematchly, a tedy neobsahují nic, a nebo obsahují to větší z čísel.
Úkol se jak zadáním, tak stylem řešení dosti podobá poslednímu úkolu z předchozího dílu. Řešitelé, kteří si toto uvědomili, si ušetřili trochu přemýšlení.
Úkol 2 byl jednodušší. Stačilo upravit příklad ze zadání na správné
uzávorkování a uvědomit si, jak se dá výraz negovat. Jedna z variant byla typu
s/(?!A).*//. Druhá nepoužívala rozhlížení, ale referenci –
s/(A)|.*/$1/.
V prvním případě pokud A vyhovuje, tak se nepokračuje dál, tedy
.* nic nepožere a nic se nesmaže, jinak se smaže všechno. Ve druhém
případě se matchne buď A a nahradí se za sebe sama, nebo se matchne
všechno a $1 bude prázdná.
I zde si rozebereme autorské řešení, řešení účastníků se prakticky nelišila.
s#^(?!([^<>]*(<([[:alnum:]]+)>(?1)</\3>[^<>]*)*)$).*$##Regex nejprve přečte veškerý prostý text. Pak je zde velká ohvězdičkovaná závorka, ve které se matchne otevírací tag, uzavírací tag, další následný prostý text a spustí se celý regex rekurzivně na vnitřek tagu. Rekurze se zastavuje tím, že ona velká ohvězdičkovaná závorka nematchne ani jednou.
Negace regexu je prvního uvedeného typu. Má to tu výhodu, že se zbytečně
nenahrazuje za $1, takže se řetězec celý nepřepisuje, pokud to není potřeba.
Na efektivitu je vůbec u složitějších regexů potřeba dát pozor. ať už z hlediska spotřebovaného času, nebo paměti. Vezměme si například regex
s/^(a{0,10000}){0,10000}$//,
který vypadá na první pohled nevinně. Nicméně Perl jej nedokáže zoptimalizovat
a na vstupu aaaaaaaaaaaaaaaaaaaaaaaaab už běží několik vteřin…
Nicméně takové problémy jsem při opravování nehledal a neřešil.