Gordon Brown se omluvil 10. září 2009. Vyjádřil se v tom smyslu, že je mu to celé moc líto a že za všechny, kteří díky Turingově práci mohou žít ve svobodě, říká, že… je mu celá věc moc líto. Učinil tak díky petici, kterou zařídil jistý britský programátor.
Druhá série dvacátého třetího ročníku KSP
Celý leták v PDF.
- Termín série: 6. prosince 2010 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 23-2-1: Balíčky balíčků
- 23-2-2: Zastavení
- 23-2-3: Projížďka
- 23-2-4: Plánování
- 23-2-5: Zaměřování
- 23-2-6: Testovací
- 23-2-7: Regulomaty
23-2-1 Balíčky balíčků (10 bodů)
 Petice byla samozřejmě elektronická, ale aby ji pan premiér nemohl
zamést pod koberec, rozhodne se ji její iniciátor John Graham-Cumming
vytisknout a zaslat poštou. Poprvé po mnoha letech studuje poštovné a co nevidí?
Petice byla samozřejmě elektronická, ale aby ji pan premiér nemohl
zamést pod koberec, rozhodne se ji její iniciátor John Graham-Cumming
vytisknout a zaslat poštou. Poprvé po mnoha letech studuje poštovné a co nevidí?

Výhodné nabídky balíčků! Můžete poslat jeden o váze N kg, dva o váze N-1 kg, tři o váze N-2 kg, …, N o váze 1 kg, kde N závisí na ročním období, denní hodině a sjízdnosti silnic. To vás nemusí trápit, N dostane váš program na vstupu.
Dále dostanete váhu H petice v celých kilogramech. Vaším úkolem bude vymyslet, které nabídky balíčků je třeba vybrat, aby se do nich dohromady vešlo H kg petice, ale zároveň aby jejich kapacita byla co nejblíže tomuto H.
Je třeba zdůraznit, že „3 balíčky, každý o váze N-2 kg“ je jedna nabídka, kterou jako celek buď přijmete, nebo nepřijmete. Chcete-li poslat 3N-6 kg, je to ideální volba.
Chcete-li poslat N-2 kg a N není úplně malé (třeba N = 100), je lepší zvolit nabídku „1 balíček o váze N kg“, přestože dva kilogramy nevyužijete. Stejně dobré řešení by pak bylo vybrat „N balíčků o váze 1 kg“ a nám je jedno, které z takových dvou stejně dobrých řešení vypíšete.
Chcete-li poslat 100 kg a N=12, můžete vybrat třeba kombinaci 3×(N-2) + 3×(N-2) + 5×(N-4) = 3×10 + 3×10 + 5×8.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému CodEx. Přesný formát vstupu a výstupu, povolené jazyky a další technické informace jsou uvedeny v CodExu přímo u úlohy.
Zavedl nejvýznamější teoretický model počítače, kterému se dnes říká Turingův stroj. Můžeme si ho představit jako nekonečnou pásku popsanou symboly z nějaké konečné množiny. Nad páskou se pohybuje hlava stroje a v každém kroku výpočtu podle jednoduché tabulky pravidel přečte symbol, nahradí ho jiným, a přesune se doleva nebo doprava. Existuje teze, že práce každého rozumného (teoretického i skutečného) počítače se dá na práci Turingova stroje převést.
Na základě tohoto modelu dokázal, že neexistuje zaručeně konečný algoritmus, který by dokázal posoudit, zdali se jiný daný algoritmus na daných datech zastaví.
Tím rozhodnul Hilbertův problém z roku 1928, který se ptal po existenci zaručeně konečného algoritmu, který dostane matematické axiomy a domněnku a rozhodne, je-li domněnka z těchto axiomů odvoditelná. Zamítnul existenci takového algoritmu, protože díky formalizaci Turingova stroje uměl vyjádřit „zastaví se algoritmus na daných datech?“ jako matematickou domněnku.
Vymyslel též „Turingův test“. Jde v podstatě o člověkostřednou definici inteligence– objekt je inteligentní právě tehdy, nerozezná-li lidský pozorovatel jeho lingvistický výstup od lingvistického výstupu člověka. Takové Turingovské testování provádí každý z nás vždy, když mu píše neznámá entita po IM a nabízí výrobek.
Co na tom, že ho v mnoha (i zmíněných) věcech asi o rok předběhl Alonzo Church – Turingův přístup se ukázal být stravitelnější než Churchův lambda kalkulus.
23-2-2 Zastavení (10 bodů)
Když už jsme u toho zastavování… Máme-li spravedlivou šestistěnnou kostku, umíme na ní generovat (celá) náhodná čísla mezi 1 a 6 (včetně) se stejnou pravděpodobností 1/6. Představme si, že máme po ruce 4-, 6-, 8-, 12- a 20stěnnou kostku. Pro které hodnoty n umíme pomocí těchto kostek generovat (celá náhodná) čísla mezi 1 a n (včetně) tak, aby všechna padala se stejnou pravděpodobností a trvalo nám to zaručeně konečný počet kroků?
Pokud píšeme generovat, myslíme tím prostě, že nějaký váš algoritmus dostane kostku „zapůjčenou“ a může si s její pomocí generovat náhodná čísla, na jejichž základě nakonec spočítá požadované výsledné náhodné číslo. Jakékoli jiné náhodné generátory jsou zakázány. Nepůjde-li vám to ve vší obecnosti, zkuste ověřit, jestli (a jak) jdou vygenerovat čísla od 1 do 120.
Třeba náhodné číslo v intervalu 1 až 32 snadno získáme na dva hody výrazem (8(d4 - 1)+d8), kde d4 je číslo hozené na čtyřstěnné kostce a d8 číslo hozené na osmistěnné kostce.
To zní strašlivě neprakticky, dokud si neosvětlíme, že řetěz padal právě a jen tehdy, sešel-li se jeden ohnutý zoubek na kotouči s jednou nedokonalou pozicí na řetězu. Je pak otázka dělitelnosti, kdy se při jízdě takové dvě chyby setkají: klidně to mohlo nastávat „jen“ každých deset minut.
23-2-3 Projížďka (12 bodů)
Představme si Turinga mířícího vlakem do krajiny, kterou si chce na kole projet. Dostaneme na vstupu seznam rozcestí a cest, které vedou mezi nimi. Jeho kolo je tentokrát bezvadné, leč terén je obtížný a hlavně nevyrovnaný – některé silnice jsou krátké a klidné, dokonce vedou z kopce; jiné jsou dlouhé, klikaté a strmé, takže velmi unavují.
Turing každé z nich při pohledu do mapy přidělil celé číslo vyjadřující tuhle subjektivní obtížnost – na kladně ohodnocených cestách si bude odpočívat a na záporně ohodnocených tuhle nashromážděnou energii vydá.
Teď by od vás chtěl, abyste napsali program, který mu najde takovou cestu (včetně začátku – a může začínat na libovolném rozcestí), po které jednak projede všechny silnice právě jednou, druhak bude na každém rozcestí součet všech Turingem do té chvíle projetých silnic nezáporný a navíc se vrátí na rozcestí, na kterém začal. Chcete-li a myslíte-li si, že vám to pomůže, předpokládejte klidně, že z každého rozcestí vychází sudý počet silnic.
„[Ve filmech] se praví, že Patton a MacArthur jsou odvážní generálové. Svět bez dechu očekává jejich další neohrožené eskapády za nepřátelskou linií. Waterhouse ví, že Patton a MacArthur jsou víc než cokoliv jiného inteligentní konzumenti [prolomených šifer] Ultra/Magic. Používají je k tomu, aby zjistili, kde nepřítel soustředil síly, pak ho obejdou a udeří na místo, kde je nejslabší. To je všechno.“
23-2-4 Plánování (10 bodů)
Pořád by ale bylo poněkud nespravedlivé upřít všem spojeneckým generálům jakoukoliv tvořivost. I když vám cizí zprávy diktují, na která místa potřebujete kdy zaútočit, pořád máte omezené zdroje.
V této úloze dostanete na vstupu seznam časových intervalů zadaných přirozenými čísly, ve kterých je potřeba likvidovat nějaký výhodný cíl ploužící se za frontovou linií. Seznam je uspořádaný podle počátků těchto intervalů.
Chceme od vás, abyste našli minimální počet bombardérů, který stačí k likvidaci všech cílů, a jejich časový rozvrh.
Neuvažujte doby přilétání a odlétání, tankování, údržby a podobně, to už je započítáno v intervalech. Letadlo je vždy plně využito celý požadovaný interval, takže se nesnažte o nějaké triky s předčasným návratem, jedním letadlem na dvou místech apod.
Příklad vstupu:5-8 7-12 11-13 12-15
Příklad výstupu:2
1: 5-8 11-13
2: 7-12 12-15
23-2-5 Zaměřování (8 bodů)
 Historicky se matematika ve válkách používala vedle
šifrování také při všemožné balistice. Nabízíme vám touto historií velmi
vzdáleně inspirovanou úlohu:
Historicky se matematika ve válkách používala vedle
šifrování také při všemožné balistice. Nabízíme vám touto historií velmi
vzdáleně inspirovanou úlohu:
Dostanete na vstupu pozici dvou kanónů v kartézské soustavě souřadnic a po řadě vrcholy i nekonvexního mnohoúhelníka (ale žádné dvě jeho nesousedící hrany se neprotínají), na jehož obvod šílený velitel přikázal střílet. Souřadnice nemusí být celá čísla.
Navíc vyžaduje, aby oba kanóny střílely na takový bod na obvodu, pro který platí, že je obsah trojúhelníka určeného oběma kanóny a tímto bodem co nejbližší zadanému číslu. Pokud je jich více, vypište libovolný z nich.
Příklad vstupu (kanóny, pevnost, obsah):
[1, 1] [1, 2]
[2, 1] [2, 2.5] [3.71, 2.5] [3.71, 6] [7, 1]
1
Odpovídající výstup může být třeba [3, 1].
23-2-6 Testovací (10 bodů)
Potřebujeme-li u takového jednoduchého počítače otestovat bezchybnost, chceme nějakou dosti jednoduchou úlohu, po jejímž vyřešení a naprogramování si budeme moci být jisti, že pokud dává počítač špatné výsledky, není to naším naprogramováním.
Co třeba takovou?
Máte zadanou setříděnou posloupnost přirozených čísel a chcete vypsat všechny trojice ve tvaru a, a+k, a+2k (pro všechna možná přirozená a, k), které se v ní nacházejí.
Příklady (vstup → výstup):
1 2 3 5 8 9 → 1-2-3 1-3-5 1-5-9 2-5-8
1 2 4 5 10 11 → nic (zde není žádná taková trojice)
Každopádně se všeobecně soudí, že ho k tomu dohnaly dosti nepěkné vedlejší účinky prováděného léčení a to je oním důvodem, proč se mu britský premiér po 55 letech omluvil.
Mezi informatiky je Turing oblíbený, protože jeho životní příběh dokumentuje, jak může být takový teoretik užitečný, když vyvstanou velké praktické problémy. Existují odhady, podle kterých analytici z Bletchley Parku zkrátili válku o rok a zachránili milion lidí, a je samozřejmé nemožné říct, jestli tomu tak je. Je rozhodně dojemné si uvědomit, že po válce samozřejmě jako hrdinové oslavováni nebyli, protože britská vláda nechtěla, aby se o prolomení daných šifer vědělo. Mnoho jich tedy, stejně jako Turing, zemřelo bez jakéhokoliv uznání.
V češtině vyšla v edici Aliter popularizační knížka „Muž, který věděl příliš mnoho“, která se celá věnuje Turingově životu a snaží se jemně vysvětlovat jeho výsledky. Pokud vás zajímá teoretická informatika a chcete být drsní, Charles Petzold nedávno sepsal „Annotated Turing“, což je přetisk Turingovova ústředního článku s poznámkami.
Existuje docela známá beletristická knížka o kryptoanalyticích z Bletchley Parku a špionážních tanečcích kolem, která se jmenuje „Enigma“ – dokonce podle ní natočili film. Tam už ale našeho hrdinu nenajdete.
23-2-7 Regulomaty (12 bodů)
 Po představení syntaxe regulárních výrazů se podíváme na zoubek tomu, co se
s nimi děje uvnitř počítače.
Po představení syntaxe regulárních výrazů se podíváme na zoubek tomu, co se
s nimi děje uvnitř počítače.
Proč se vlastně oněm výrazům říká regulární? Popisují totiž regulární jazyky, tedy jazyky rozpoznávané konečnými stavovými automaty. Že nevíte, o čem píšu?
Konečný automat je množina (Q, A, δ, q0, F) … formální definici nechme na seriál 17. série a úlohu 17-2-5.
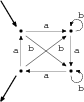
Konečný automat si představme jako množinu stavů, mezi kterými můžeme různě přecházet tím, že přečteme znak ze vstupu. Ilustrativní obrázek napoví víc než suchá teorie. Tlusté šipky symbolizují vstupní stav a výstupní stavy.
Výstupem našeho automatu pak bude přijetí, nebo odmítnutí, podle toho, jestli řetězec vyhovuje, či nikoli.
Na začátku jsme v počátečním stavu. Přečteme písmenko ze vstupu a vybereme si příslušnou hranu a po ní přejdeme do dalšího stavu. A zase přečteme písmenko ze vstupu, vybereme si hranu, přejdeme…
Když nemáme co přečíst, stačí nám jednoduše zjistit, jestli jsme zrovna ve výstupním stavu, nebo nikoli. Pokud jsme ve výstupním stavu, tak jsme přijali vstup, jinak ho odmítneme. Vstup taktéž odmítneme, pokud při běhu zjistímě, že z aktuálního stavu žádná vhodná hrana nevede.
Automat na obrázku tedy přijímá taková slova jako bba, bababa, aaaaaaa, ale odmítne například slova abba, baba (skončí vpravo
dole), ababab (skončí vpravo nahoře), aaaa nebo
λ(to je obvykle používaná zkratka pro prázdné slovo;
(skončí vlevo nahoře).
Existuje hezká věta, která říká, že každý konečný automat lze převést na regulární výraz. To znamená, že umíme najít regulární výraz, který (regex něco matchuje = regexu vyhovuje něco) matchuje právě ty vstupy, které přijme konečný automat (a žádné jiné). Důkaz té věty se dá udělat třeba ukázáním univerzálního postupu, který ale bude až v autorském řešení, jinak byste přišli o tu zábavu vymýšlet, jak na to.
Úkol 1 [4b]
Převeďte automat na obrázku na regulární výraz:
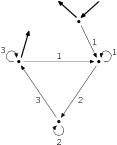
Nebylo to tak hrozné, ne? Co si to vzít obráceně? Existuje docela hezká věta, která dokazuje, že každý regulární výraz lze převést na konečný automat.
Některé jdou i ručně.
Úkol 2 [3b]
Převeďte zadaný výraz na konečný automat:
(1(23|32)|2(31|13)|3(12|21))*
Čím méně hran a stavů, tím více bodů máte šanci získat (za automat mající více než 10 stavů nebudou ani 2 body).
Drtivou většinu výrazů ale hned tak jednoduše převést nepůjde, nebo to alespoň není na první pohled vidět. Zavedeme proto nedeterministické konečné automaty (NKA).
NKA je automat, u kterého může z jednoho stavu vést více hran pro jedno písmenko. Program si tedy může vybrat, kterou cestou půjde. Vstup je pak přijat, pokud existuje možnost, jak ho přijmout, neboli pokud existuje vhodná cesta (tedy po které program mohl jít), která končí v nějakém z výstupních stavů.
Navíc si dovolíme takzvané ε-přechody. To jsou hrany, po kterých je možno přejít, aniž přečteme znak ze vstupu. Aby bylo poznat, že jsme k hraně nezapomněli připsat její znak, píšeme k ní ε – symbol pro prázdný řetězec.
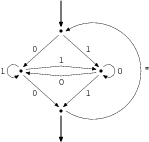
Tento automat přijímá třeba řetězce 10111, 1111, ale třeba ne
000 nebo 111. Vyzkoušejte si sami, jak.
Úkol 3 [5b]
Převeďte výraz (10(1(10)*1)*01)* na NKA s ε-přechody.
Bonus 2b pro ty, kdo vymyslí jednodušší (tedy kratší) ekvivalentní výraz.