Pátá série dvacátého třetího ročníku KSP
Celý leták v PDF.
Zadání úloh
John von Neumann se narodil v Maďarsku (vlastně v Rakousku-Uhersku) v roce
1903 a zemřel v roce 1957 ve Spojených státech. Byl to velmi univerzální
vědec – pracoval na matematice čisté i aplikované a významnou měrou přispěl k rozvoji počítačů.
S jeho jménem se jde občas potkat dokonce i ve středoškolské výuce
informatiky, kde je často jmenována „von Neumannova architektura“, jejíž
hlavní rys tkví v jediné paměti pro program i data.
Něco takového je skutečně dobrý nápad, který stojí za dnešní univerzálností
počítačů, ale tehdy to byl velmi pokrokový koncept, neboť první výpočetní
stroje se programovaly přepojováním drátů.
Vymyslel také jednoduchý a ne zcela nepoužitelný způsob generování
pseudonáhodných čísel, který funguje tak, že předchozí vygenerované náhodné
číslo umocníme na druhou a vezmeme z jeho desítkového zápisu prostřední část,
kterou ohlásíme jako nové „náhodné“ číslo.
Von Neumann si byl vědom omezení podobných (pseudonáhodných) metod pro
generování čísel a známý je jeho výrok „každý, kdo chce generovat náhodné
číslice aritmetickými prostředky, je hříšník“. On sám jich však potřeboval
neobvykle hodně pro náhodné simulace vodíkové bomby, a tak vzal zavděk takovýmto
hříšným způsobem.
Společně se Stanisławem Ulamem je uváděn jako průkopník buněčných automatů,
zjednodušených modelů vývoje fyzikálních systémů. Podařilo se mu v jednom
takovém modelu vytvořit sebereplikující stroj a napsal na toto téma celou
knihu. Navrhoval podobné sebesestavující stroje použít pro rozsáhlé těžební
operace, kde by obvyklá tovární výroba potřebných strojů stála lidstvo
přílišné úsilí.
Podobné myšlenky posledních několik desítek let budí hrůzu technologických
nadšenců, kteří předvídají, že nanotechnologie umožní stavbu tak dobrých
sebereplikujících jednotek, že na sebe přemění celou planetu. Ostatně o tom
byl jeden z posledních proužků na xkcd.
23-5-1 Boj s nanoboty (11 bodů)
Přeneseme se teď do fiktivního světa knihy Diamantový věk, ve
které nejrůznější nanoboti vesele poletují po světě a zkázu světa to nevyvolá.
Existují totiž certifikační organizace, které pomocí svých bojových nanobotů
vynucují, aby měl každý stroj, který se chce pohybovat v ovzduší, jisté
nanorazítko, které zaručuje jeho bezpečnost.
Pokud se zloduch rozhodne, že zaplaví svět necertifikovanými nanoboty, nastane
„tonerová válka“ – nanoboti se do sebe pustí, lidé z jejich zbytků dostanou
rakovinu plic a vymřou.
Mějme kousek světa zadaný jako čtvercovou síť. Na prvním řádku dostaneme M;
na každém z následujících M řádků dostaneme souřadnice města xi a yi,
počet obyvatel Ci a čas příchodu padoucha Ti.
Náš hrdina chce předejít tonerové válce a z ní vyplývajícím zdravotním rizikům
pro obyvatele daného města. Proto cestuje po mapě a snaží se v tom padouchovi
zabránit. Povede se mu to vždy tehdy, když je ve správný čas ve správném městě.
Hrdina začíná na políčku (0,0) v čase 0 a za jednotku času se může
přemístit na sousední políčko, nebo zůstat stát.
Vaším úkolem je najít posloupnost měst, které má navštívit, aby zachránil co
nejvíce lidí.
Například pro vstup
4
1 6 1000 18
2 7 300 16
3 3 100 11
6 5 500 11
program odpoví 4 1 (zachrání 1500 lidí).
Řešení
Podílel se na konstrukci atomové bomby. Na rozdíl od většiny ostatních
významných vědců projektu Manhattan se dokonce zapojil do navazujícího programu
pro vývoj bomby vodíkové.
Označoval své názory za
„militantnější, než je obvyklé“ a prosazoval kupříkladu preventivní jaderný
úder na Sovětský svaz předtím, než si obstará vlastní jaderné zbraně.
Postupně se tak zapojovoval do různých armádních poradních sborů. Přišel na
to, že je efektivnější nechat detonovat atomovou nálož vysoko nad zemí, než
při dopadu.
Zúčastnil se tedy třeba komise pro výběr japonských měst, nad
kterými bude bomba použita, aby pomohl spočítat případné japonské ztráty.
23-5-2 Zjednodušení situace (13 bodů)
 Když je mapa bitevního pole moc nepřehledná, odstraní
se méně významné jednotky, popř. se sdruží pod souhrnnou vlaječku. Mohli bychom
ale v takové situaci chtít zazoomovat na část bitevního pole tak, aby se
nezměnil zobrazený poměr sil.
Když je mapa bitevního pole moc nepřehledná, odstraní
se méně významné jednotky, popř. se sdruží pod souhrnnou vlaječku. Mohli bychom
ale v takové situaci chtít zazoomovat na část bitevního pole tak, aby se
nezměnil zobrazený poměr sil.
Na vstupu dostaneme 2N pozic vojáků naší strany a 2M pozic vojáků
nepřítele; 2N,2M ∈[2,600]. Pozice budou dvojice nezáporných
celých čísel v intervalu [0,100 000].
Úkolem bude najít takovou přímku, která rozdělí bojiště na dvě části, kde
v každé z části leží právě N našich vojáků a M nepřátel. Přímku vypište
jako trojici desetinných čísel (a,b,c) (ve výstupu oddělených mezerou), což
jsou koeficienty v rovnici přímky ax + by + c = 0.
Můžete předpokládat, že se žádné tři body na vstupu nenacházejí na jedné
přímce. Na dělicí přímce nesmí ležet žádný ze zadaných bodů.
Pokud přímek bude několik, stačí vypsat libovolnou z nich.
Na vstupu jsou na prvním řádku čísla 2N a 2M, následuje 2N+2M řádků, na
každém jsou dvě celá čísla oddělená mezerou – souřadnice vrcholů. Nejdříve
jsou uvedeny naše pozice, poté pozice nepřátel.
Příklad vstupu:
4 2
0 0
0 4
4 0
4 4
2 1
2 8
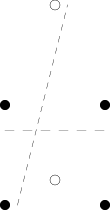 Dvě možná řešení jsou na obrázku vpravo.
Dvě možná řešení jsou na obrázku vpravo. 4 -1 -2 (krátké čárky) nebo
0 1 -3 (dlouhé čárky).
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
V oblasti čisté matematiky pracoval na jejích základech – dnešní způsob
množinové definice přirozených čísel pochází právě od něj.
Možná znáte algoritmus Minimax, kterým se dá naučit počítač hrát piškvorky,
ale i mnohé další hry. Von Neumann stál u zrodu teorie her a formuloval a
dokázal tzv. minimaxovou větu.
Mimimaxová věta využívá principu „své tahy volím jako nejlepší, u tahů
nepřítele počítám s nejhorším pro mě“ k tomu, aby u her dvou hráčů
(s nulovým součtem)
prohlásila, že jeden hráč může nejlépe vyhrát stejnou měrou, jako
může druhý hráč nejlépe (tj. nejméně) prohrát.
23-5-3 Hra pro jednoho hráče (9 bodů)
 Hry pro dva hráče známe z běžné zkušenosti – piškvorky
jsou jejich nejběžnějším zástupcem. Řekneme-li „hra pro jednoho hráče“,
napadne nás nejspíš něco jako solitaire.
Hry pro dva hráče známe z běžné zkušenosti – piškvorky
jsou jejich nejběžnějším zástupcem. Řekneme-li „hra pro jednoho hráče“,
napadne nás nejspíš něco jako solitaire.
Zajímavá věc – existuje i pojem „hra pro žádné hráče“ a myslí se tím třeba
již zmíněný buněčný automat (například Game of Life Johna Conwaye), kdy je celý
průběh jeho vývoje určen počátečním stavem a jde se na něj jen koukat.
Hra, kterou budeme v této úloze uvažovat, počítá s hráčem jedním. Jmenuje se
Hanojské věže a spočívá v tom, že dostanete tři tyče A, B a C a na tyči
A máte navlečeny disky se zmenšujícím se průměrem (nahoře je nejmenší).
Vaším úkolem je přemístit při zachování pořadí disky z tyče A na tyč C.
Jediný tah, který máte povolen, je přemístění svrchního disku z libovolné tyče
na jinou, ale pouze tehdy, pokud je disk menší, než svrchní disk na cílové
tyči.
Pro tuto známou hru existuje jedinečná vyhrávající strategie, která má 2n-1
tahů a na kterou není těžké přijít. Pro tři disky vypadá kupříkladu
tak,
že se ten nejmenší přesune na tyč C, střední na tyč B, nejmenší na tyč B,
největší na tyč C… a pak už je to jasné.
Vaším úkolem v této úloze není tuto strategii zahrát. Dostanete na vstupu
počet disků D a číslo N a vypíšete, jak bude vypadat stav hry s D
disky po odehrání N kroků této optimální strategie.
Třeba pro D=3 a N=3 je na tyči A disk největší, na tyči B disk střední a
nejmenší a na tyči C není disk žádný.
Řešení
I o von Neumannovi se vypráví řada veselých příhod. Byl prý špatný, ale
vášnivý řidič a často si za volantem četl.
23-5-4 Model čtoucího řidiče (11 bodů)
Mějme řidiče, jenž kvůli kvalitní beletrii nemá dost pozornosti na sledování
informačních tabulí, které by mu pověděly, kam která odbočka vede. Jezdí po
silniční síti, která je zadaná ohodnoceným orientovaným grafem (tj. každá
silnice je jednosměrka), kde budeme každý vrchol chápat jako kruhový objezd a
dostaneme s ním na vstupu i cyklické pořadí hran.
Protože řidič nesleduje cedule, vyjede vždy na nejbližším možném následujícím
výjezdu. Vaším úkolem je najít pro něj orientovanou cestu s nejnižším možným
součtem ohodnocení, která prochází každým vrcholem právě jednou.
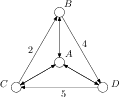
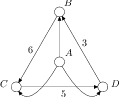
Pro případ vlevo řešení neexistuje, pro případ vpravo je řešením
A–C–D–B. Hrany bez čísel chápejte jako ohodnocené 1.
Řešení
Stephen Wolfram o von Neumannovi k stému výročí narození
napsal,
že se oddaně držel aktuálních trendů vývoje matematiky a že je překvapivé, že
člověk tak inteligentní jako on nikdy nepřišel s žádným skutečně originálním
a nečekaným výsledkem, ke kterým měl ve své době opravdu blízko.
Gödelovy věty či Turingův stroj mohly velmi dobře pocházet i od něj. „Von
Neumannova architektura“ se sice stala velmi vlivným konceptem, jistě však
nešlo o první myšlenku svého druhu, o několik let ho s ní předběhnul
kupříkladu Turing.
Vysvětluje si to jednak tím, že mu současné metody šly aplikovat tak hladce,
že k odvážným výletům za hranice obvyklého necítil potřebu, druhak tím, že byl
konformní člověk, který ctil autority a stejně jako byl zadobře s americkou
vládou a armádou, tak nechtěl zpochybňovat velká Hilbertova přesvědčení, proti
kterým zmíněné originální výsledky šly.
Podle pamětníků to byl velmi společenský a přátelský člověk. Každý týden
uspořádal dva večírky a měl rád děti. Rád vyprávěl obhroublé vtipy. Jeho
relativně brzká smrt nebyla tak tragická (dá-li se srovnávat) jako v případě
zmíněného Gödela nebo Turinga – měl rakovinu a do poslední chvíle pracoval.
23-5-5 Kuchařková (12 bodů)
Následující problém si pojmenujeme Metr a vaším úkolem je
dokázat, že je NP-úplný.
Jistě znáte skládací metry. Mají typicky pět článků po dvaceti centimetrech.
Mějme metr nepravidelný, jehož jednotlivé články jsou různě dlouhé. Tyto délky
dostaneme v pořadí na vstupu, stejně tak délku pouzdra, do kterého bychom
chtěli metr uložit.
Podaří se nám to? Pro články délek 6, 3, 3 a pouzdro délky 6 odpověď jistě zní
ano, pro vstup 6, 3, 4 a stejně dlouhé pouzdro to už ale nepůjde.
Řešení
23-5-6 Předposlední (13 bodů)
Dostanete na vstupu orientovaný graf s kladně celočíselně
ohodnocenými hranami. Dále tam bude pro každý vrchol dvojice kýžených limitů
– minimální součet vstupních hran a maximální součet výstupních hran.
Vaším úkolem je najít nové nezáporné celočíselné ohodnocení každé hrany, které
nebude větší než to původní a které bude dohromady se všemi ostatními novými
ohodnoceními respektovat dané limity.
Řešení
23-5-7 Perlím, Perlíš, Perlíme (15 bodů)
 Tento text navazuje na předchozí série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.
Tento text navazuje na předchozí série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.
V závěrečném díle seriálu si ukážeme, kam došlo všemožné rozšiřování regexů
v Perlu – jazyce určeném zvláště na zpracování textu. Nebudeme probírat
kompletní PerlRe, kdybyste se o nich chtěli dozvědět více, přečtěte si
přehlednou dokumentaci.
První kroky v Perlu
Nejprve je potřeba Perl nějak získat. Pokud máte Linux, máte jej už
pravděpodobně dávno nainstalovaný, jen o něm nevíte. Kdybyste jej náhodou
neměli, nainstalujte si jej z balíčkovače, mají jej snad všechny rozumné
distribuce.
Na Windows si nainstalujte Cygwin, někteří jej
asi máte už od minulé série. V něm by měl Perl jít nainstalovat.
Do Cygwinu se balíčky doinstalovávají spuštěním setupu, člověk si vybere nějaký
server a dostane se na seznam balíčků. Tam dá vyhledat, co potřebuje, zaškrtne,
odklikne a při příštím spuštění Cygwinu může nové balíčky používat.
Perl je programovací jazyk mnoha zajímavých vlastností, zájemci o více
informací si přečtou rozsáhlou dokumentaci,
případně se zeptají na fóru.
My si ukážeme jenom minimální program, který můžete používat k testování svých pokusů s PerlRe.
#!/usr/bin/perl
use strict; use warnings; # hlídací pes
# cyklus přes všechny řádky vstupu
while (<>) {
# sem pište své příkazy
# nahraď všechny bagry za kombajny
s/bagr/kombajn/g;
# sem už své příkazy nepište
# výpis
print;
}
Tenhle program čte vstup po řádkách, pro každý řádek provede zadané příkazy a
pak jej vypíše. Každý příkaz končí středníkem; komentáře jsou uvozeny
znakem # (kriminál), od něj dál se všechno ignoruje.
Jak spustit program? V terminálu dojděte do příslušné složky (pomocí cd)
a napište perl minimal.pl, pokud jste pojmenovali svůj minimální program
minimal.pl (obvyklá přípona programu v Perlu je .pl).
Pak na vstup píšete podobně jako u sedu; ukončit vstup je možné stiskem
Ctrl+D. Uvedený program by tedy převedl vstup (vlevo) na výstup (vpravo):
Žlutý bagr
Modrý kombajn
Mám dva bagry.
bagrbagrbagr
|
Žlutý kombajn
Modrý kombajn
Mám dva kombajny.
kombajnkombajnkombajn
|
Nuže, po technickém úvodu přijde konečně něco o regexech (které také budeme
v tomto textu označovat jako PerlRe).
Základní regexy
Existují dva typy regexových příkazů. Prvním z nich je regex ve stylu
grep, který zjišťuje, jestli je na vstupním řádku vyhovující podřetězec.
Vypadá třeba takhle: m#cosi#.
První písmenko je vždycky m, druhé písmenko je oddělovač, pak následuje
hledaný regex (ve kterém je případně oddělovač nutno escapovat, viz níže) a pak
zase oddělovač. Používá se třeba v podmínkách:
print "obsahuje bagr\n" if m/bagr/;
Další z mnoha využití je při parsování vstupu:
# $1 = hodiny, $2 = minuty, $3 = vteřiny
m/(..):(..):(..)/;
print "Je $3. vteřina";
Takovéhle programy už ale psát nebudeme, zůstaneme jen u samotných regexů.
Druhý typ je nahrazovací – s#bagr#kombajn#g. Písmenko s,
oddělovač, regex, oddělovač, čím nahradit, oddělovač, modifikátory (ty se
ostatně mohou objevit i u prvního typu). Příkaz nalezne první výskyt regexu a
nahradí jej zadaným řetězcem. Je-li uveden modifikátor g, nalezne příkaz
všechny nepřekrývající se výskyty a pak je najednou nahradí.
Příkaz s/rr/tr/g; tedy převede vstup (vlevo) na výstup (vpravo):
rr
rrr
rrrr
rrrrr
|
tr
trr
trtr
trtrr
|
Jak vypadá oddělovač? Může to být nějaký ze znaků
!"#$&%)*+,-./:;=>?@\]^`|}~,
případně je možné použít
konstrukci s(a)(b)g (a analogicky s {}, <> a []).
Jak vypadá výraz? Regexy, které jsme si definovali v prvním díle, by měl Perl
přijmout bez řečí. Backreference fungují také stejně, jen jich může být
libovolně mnoho. Navíc pokud není reference použita přímo ve výrazu, neodkazuje
se na ni \4, ale $4 (nebo třeba $2078). Takže například
takhle: s/(.*)(.*)\2\1/$2$1$1$2/
Rozhlížecí předpoklady
Anglický název je „Look-around assertions“, kdybyste si o tom chtěli přečíst
v manuálu.
Taková typická konstrukce je s/bagr(?=b)/rýč/g. Té vyhovuje
bagr, pokud za ním je písmeno b. To však již není zahrnuto do
onoho řetězce, takže z řetězce bagrbagrbagry udělá rýčrýčbagry.
Jak vypadají tyto konstrukce formálně? (?=Výraz) vyhovuje, pokud na
tomto místě začíná kus řetězce, který mu vyhovuje. Pak se Perl vrátí na
jeho začátek a tváří se, jako by tím kusem řetězce ještě nikdy neprošel. Třeba
výrazu ^(?=(..)*$)(...)*$
vyhovují všechny řádky, na kterých je počet znaků dělitelný šesti.
Konstrukce (?!výraz) dělá téměř totéž, akorát v negaci. Vyhovuje, pokud
se Perlu nepodaří najít žádný vyhovující řetězec začínající na tomto místě. Po
tomto zjištění se Perl vrátí na jeho začátek a pokračuje, jako by se
nechumelilo.
Ještě existují podobné konstrukce v obráceném směru. Předešlé dvě byly
„koukni dopředu“, následující budou „koukni zpátky“.
Chcete-li tedy Perlu říct „Tady zastav a zjisti, jestli na tomto místě končí
řetězec vyhovující výrazu,“ použijete konstrukci (?<=výraz); pokud chcete negaci,
neboli zajistit, aby na tomto místě nekončil žádný vyhovující řetězec,
napíšete (?<!výraz) – například výrazu .*(?<!bagr) vyhovují
všechny řetězce, které nekončí „bagr“.
Výrazy typu „koukni dozadu“ mají jedno nepříjemné omezení. Musí mít fixní
délku. To znamená, že v nich nejen nesmí být kvantifikátory, ale ani třeba
(a|bb)– dvě varianty různé délky.
Rekurze
Držte si klobouky, jedeme s kopce. Jak vyrobit výraz, kterému by vyhovoval
palindromický řádek? Tenhle to je!
^((.)(?1)\2|.?)$
Co je na něm tak zajímavého? Ten malinký kousek (?1), který říká něco
takového: „Najdi závorku, na kterou by ses normálně odkazoval pomocí
$1. Ten výraz, který je uvnitř, jako bys spustil na tomto místě…“
Nejlepší bude asi rekurzi předvést na příkladech. Onen první je velice
jednoduchý. Celý se skládá ze dvou alternativních větví – v první probíhá
rekurzivní krok, druhá funguje jako ukončovací podmínka.
První větev vezme první znak, spustí rekurzi a zbytek pak zase musí být první
znak. Rekurze končí ve chvíli, kdy dojde doprostřed testovaného řetězce –
zbývá tam prázdný řetězec (v palindromu sudé délky) nebo prostřední znak,
který je sám sobě párovým. Přesně o to se stará druhá větev.
Za připomenutí stojí, že závorky se číslují podle pozice jejich otevírací
závorky zleva doprava.
Ještě si uvedeme jeden rekurzivní příklad – regex, kterému vyhovují všechna
správná uzávorkování. Prozkoumejte si jej sami.
(\((?1)*\))*
Úkol 1 [9b]
Na řádku jsou vždy dvě různá kladná celá čísla zapsaná ve dvojkové soustavě
oddělená mezerou. Napište (jeden) substituční výraz, který na řádku zanechá to
větší z nich.
Tedy na vstup (vlevo) dostanete výstup (vpravo):
1001 1101
11100 11
100 1111
|
1101
11100
1111
|
Úkol 2 [6b]
Na každém řádku vstupu je pseudoXML. Jsou povolené jen párové tagy bez
atributů a prostý text libovolně mezi nimi a okolo. Název tagu (řetězec
nenulové délky mezi < a >) smí být složen pouze
z [[:alnum:]] znaků. Prostý text nesmí obsahovat znaky < a
>.
Váš (jeden) substituční výraz zkontroluje validitu každého řádku na vstupu,
tedy jestli má každý tag příslušný uzavírací a jestli se tagy nekříží. Pokud je
řádek validní, nechá jej být, v opačném případě jej smaže (nahradí prázdným
řetězcem).
Ze vstupu
xx<a>ehm<b>sgfd</b>dfsd</a>
xx<a>ehm<b>sgfd</a>dfsd</b>
nechá program jen první řádek.
Připomínám, že k řešení patří zdůvodnění. Zvláště u této série si dejte záležet
na popisu jednotlivých částí regexů, stejně jako na zdůvodnění správnosti.
Používejte k řešení jen tu část PerlRe, kterou jsme si zde vyložili, ať mají
všichni stejné podmínky.
Řešení
 Když je mapa bitevního pole moc nepřehledná, odstraní
se méně významné jednotky, popř. se sdruží pod souhrnnou vlaječku. Mohli bychom
ale v takové situaci chtít zazoomovat na část bitevního pole tak, aby se
nezměnil zobrazený poměr sil.
Když je mapa bitevního pole moc nepřehledná, odstraní
se méně významné jednotky, popř. se sdruží pod souhrnnou vlaječku. Mohli bychom
ale v takové situaci chtít zazoomovat na část bitevního pole tak, aby se
nezměnil zobrazený poměr sil. Dvě možná řešení jsou na obrázku vpravo.
Dvě možná řešení jsou na obrázku vpravo.  Hry pro dva hráče známe z běžné zkušenosti – piškvorky
jsou jejich nejběžnějším zástupcem. Řekneme-li „hra pro jednoho hráče“,
napadne nás nejspíš něco jako solitaire.
Hry pro dva hráče známe z běžné zkušenosti – piškvorky
jsou jejich nejběžnějším zástupcem. Řekneme-li „hra pro jednoho hráče“,
napadne nás nejspíš něco jako solitaire.

 Tento text navazuje na předchozí série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.
Tento text navazuje na předchozí série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.