První série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
Zadání úloh
FD 60 BK 120 FD 60 RT 90 FD 50
LT 90 FD 60 BK 120 FD 60
10 PRINT "e"
++++++++++[>+++++++++++<-]>--.
Ook. Ook. Ook. Ook. Ook. Ook. Ook. Ook.
Ook. Ook. Ook. Ook. Ook. Ook. Ook. Ook.
Ook. Ook. Ook. Ook. Ook! Ook? Ook! Ook!
Ook. Ook? Ook. Ook. Ook. Ook. Ook. Ook.
Ook. Ook. Ook. Ook. Ook. Ook. Ook. Ook.
Ook. Ook. Ook. Ook. Ook. Ook. Ook? Ook.
Ook? Ook! Ook. Ook? Ook. Ook. Ook. Ook.
Ook. Ook. Ook. Ook. Ook. Ook. Ook. Ook.
Ook. Ook. Ook. Ook. Ook! Ook. Ook? Ook.
print split /[^g-q]/, lc sub {};
#include <stdio.h>
int main() {
printf("%c", (107^25)-70&99);
return 0;
}
h(X,[]) :- put(X), !.
h(X,[A|B]) :- Y is X + A, h(Y,B).
?- h(42, [5, 6, 7, 8, 7]).
IDENTIFICATION DIVISION.
PROGRAM-ID. SERIE1.
PROCEDURE DIVISION.
DISPLAY 'S'.
STOP RUN.
(defun gen (i j)
(if (<= i j)(cons i (gen (1+ i) j)) nil))
(defun split (s)
(mapcar (lambda (i) (substring s (1- i) i))
(gen 1 (length s))))
(defun GAPS (x)
(princ (caddr (split (symbol-name x)))))
(defun Q (x)
(eval (list x (list 'quote x))))
(Q 'GAPS)
class Program {
static void Main() {
System.Console.Write((char)0x21);
}
}
Toto je jen malý náhled do zvěřince programovacích jazyků. Dokážete rozpoznat
jednotlivé jazyky? Umíte zjistit, co programy v nich udělají a co z toho
vznikne dohromady? Pokud ne, může vám pomoci malý výlet do historie.
První předzvěstí programovacího jazyka byl v roce 1801 vynález tkalcovského
stavu ovládaného děrnými štítky (kartami z tvrdšího papíru, jež obsahovaly data
zakódovaná do děr). Jednalo se však spíše o kód než jazyk.
Dalším významným počinem se stalo v půli 19. století napsání prvního programu,
a to na počítání Bernoulliho čísel. Kupodivu ho nenapsal muž, ale Ada Lovelace
v korespondenci s Charlesem Babbagem pro jeho analytický stroj.
Až doba elektromechanických počítačů z konce 30. let a ze 40. let 20. století
odstartovala rychlý vývoj programovacích jazyků. Hybatelem pokroku byla
nepřekvapivě druhá světová válka, zejména touha prolomit šifry nepřátelské
strany.
Tehdy se programovalo pomocí přepínačů či děrných štítků (v podstatě sekvencí
0 a 1) a pro každý počítač jinak (bylo jich tehdy naštěstí jen několik na světě).
Problémy tohoto způsobu se však objevily celkem rychle, především v množství
chyb, jež raní programátoři udělali.
To vedlo k vývoji vyšších jazyků. První návrh, pojmenovaný Plankalkül, vymyslel
Konrad Zuse (autor elektromechanických počítačů Z1, Z2, Z3 a Z4), nikdy ho však
neimplementoval.
Po strojových kódech přišly „assemblery“, které nahrazovaly binární zápisy
anglickými slovy jako „add“ a „xor“.
24-1-1 Podvádíme s XORem (8 bodů)
 Představte si, že jste s kolegou z práce dostali obrovskou hromadu hardwarových
součástek, přičemž každá má nějakou cenu danou přirozeným číslem. Chcete je
rozdělit na dvě části, aby byl v obou stejný součet cen.
Představte si, že jste s kolegou z práce dostali obrovskou hromadu hardwarových
součástek, přičemž každá má nějakou cenu danou přirozeným číslem. Chcete je
rozdělit na dvě části, aby byl v obou stejný součet cen.
Kolega však není váš kamarád, a tak ho zkusíte podvést. Vy rozdělíte součástky
na dvě hromádky a on si součty překontroluje programem v assembleru, jenže
nebude tušit, že dělá operaci xor místo sčítání (což jste mu nenápadně
prohodili).
Operace xor (exkluzivní or, neboli vylučovací nebo) pracuje se dvěma čísly po
bitech tak, že ve výsledném čísle je na i-tém místě jednička, když byla
jednička na i-tém místo právě v jednom ze vstupních čísel (tzn. ne v obou).
Příklad (čísla jsou v binárním zápisu, v závorce desítkově):
11001001 (201)
XOR 01100101 (101)
--------------
= 10101100 (172)
Máte tedy seznam přirozených čísel, který chcete rozdělit tak, aby xor
všech prvků byl v obou částech stejný, ale rozdíl součtů co největší (menší
připadne přirozeně kolegovi).
K této úloze není potřeba vymyslet algoritmus nebo napsat program, jde spíše
o nalezení způsobu rozdělování čísel.
Řešení
Prvním z moderních vyšších programovacích jazyků, jež se stále používají, je
FORTRAN (
FORmula TRANslator) z roku 1955, původně určený pro
vědeckotechnické výpočty. Stal se předchůdcem dnešních imperativních jazyků,
v nichž se program zapisuje jako posloupnost příkazů s přesně daným pořadím
vyhodnocení.
Brzy ho následoval zcela odlišný LISP (LISt Processor), první
funkcionální jazyk. Zlí jazykové mu přezdívají Lots of Irritating
Superfluous Parentheses (spousta otravných nadbytečných závorek),
protože téměř každý příkaz je ohraničen kulatými závorkami.
Funkcionální se podobným jazykům říká, protože zachází s výpočtem jako
s vyhodnocováním matematické funkce. Představují jeden z přístupů
deklarativního programování, v němž se na rozdíl od imperativního jen určuje, co se
má udělat, kdežto imperativní jazyk popisuje i postup.
Druhým rozšířeným deklarativním přístupem je logické programování, které
vzniklo začátkem 70. let. Nejznámějším zástupcem je Prolog, v němž jsou
jednotlivé části programu v podstatě logické formule.
Koncem 50. let do rodiny imperativních jazyků přibyl ALGOL (ALGOrithmic
Language) uzpůsobený pro přehlednější zápis algoritmů. Jako první přišel
s bloky příkazů, které byly vyznačeny slovy begin a end.
Že jste už begin a end někde viděli? Ano, z ALGOLu se koncem 60. let vyvinul
Pascal, nejdříve určený pro výuku programování, ovšem dodnes rozšířený i
v komerční sféře.
Od 60. let se s jazyky doslova roztrhl pytel. Jmenujme jen ty významné,
rozšířené nebo alespoň něčím zajímavé.
V roce 1964 byl vytvořen BASIC (Beginner's All-purpose Symbolic
Instruction Code), stejně jako FORTRAN a ALGOL imperativní. Při jeho vytváření
byl kladen důraz na snadné používání a podobnost angličtině. Jeho dialekty a
pokračovatelé jako Visual BASIC jsou dodnes hojně používané.
24-1-2 Rozházené řádky v BASICu (7 bodů)
 Programátorský šotek měl veselou náladu, a tak přeházel řádky ve vašem už
značně dlouhém programu v BASICu. Naštěstí je na řádcích na začátku napsáno
jejich číslo (na rozdíl od starých verzí BASICu, kde se typicky číslovalo po
desítkách, čísla v tomto programu začínají od 1 a přibývají po jedné).
Programátorský šotek měl veselou náladu, a tak přeházel řádky ve vašem už
značně dlouhém programu v BASICu. Naštěstí je na řádcích na začátku napsáno
jejich číslo (na rozdíl od starých verzí BASICu, kde se typicky číslovalo po
desítkách, čísla v tomto programu začínají od 1 a přibývají po jedné).
Soubor lze spravit pouze prohazováním dvojic řádků, ale vy se jako správní
programátoři nechcete moc nadřít a rádi byste provedli co nejméně prohození,
abyste dostali původní program.
Vymyslete algoritmus, který dostane na vstupu posloupnost N čísel od 1 do
N, v níž se žádné neopakuje (tedy permutaci), a má určit, na kolik nejméně
prohození 2 řádků lze dostat seřazenou posloupnost od 1 do N.
Příklad: pro permutaci 3, 10, 8, 4, 6, 5, 9, 1, 2, 7 je správnou odpovědí 6.
Řešení
Z konce 50. a začátku 60. let pochází také zvláštní programovací jazyk APL založený
na matematické notaci. Programy v něm jsou typicky jednořádkové a vyhodnocují
se striktně zprava doleva (tedy v APL neexistuje nic jako priorita operátorů).
Ptáte se, jak se program dokáže vejít na jednu řádku? Docela pěkně, když jsou
operátory jednoznakové, jen je pro ně třeba použít tolik znaků, že většina není
na běžných klávesnicích. Pár příkladů: % (dělení), ρ (zjištění
rozměrů pole), více jich můžete najít v předloňském seriálu.
Na počátku 70. let vznikl v Bellových laboratořích současně se systémem Unix
jazyk C vyvinutý z B (B už však nepředcházelo žádné A, zato jazyk D z přelomu
tisíciletí navazuje na C).
C bylo navrženo více nízkoúrovňově, a tudíž je vhodné na systémové a výkonově
náročné aplikace. Po svých předchůdcích zdědilo označování bloků znaky {
a }.
24-1-3 Turnaj jazyků (12 bodů)
Když už jsme si tu několik programovacích jazyků představili, můžeme mezi nimi
uspořádat velký turnaj, jehož se zúčastní i jazyk budoucnosti, BestLang. Ten je
přirozeně zcela nejlepší a vždy vyhraje.
V každém kole turnaje je zadána úloha, přední odborníci na jednotlivé jazyky
v každém napíší řešení a do dalšího kola postupují ty jazyky, jejichž programy
doběhly do dvojnásobku času nejlepšího řešení.
Jak bylo řečeno, BestLang vyhraje. Ale chce vyhrát s co nejvíce body a ty se
počítají za každé kolo vzorcem
počet vyřazených · 100 000 / počet na začátku kola.
Dělení ve vzorci je celočíselné (počítá se dolní celá část) a počet na začátku
kola obsahuje i BestLang. Celkový počet bodů určuje součet bodů ze všech kol.
BestLang je navíc tak dobrý, že si může v každém kole vybrat, kolik jazyků
vyřadí (všechna řešení v ostatních jazycích doběhnou ve skoro stejném čase a
BestLang dokáže zjistit, v jakém). V kole nemusí vyřadit žádný jazyk.
Máte daný počet jazyků (N) a počet kol (K), přičemž N≤ 1 000 a K≤ 1 000,
a úkolem je najít takovou posloupnost počtu vyřazených v jednotlivých kolech,
aby BestLang získal co nejvíce bodů.
V jakémkoliv kole může klidně vyřadit všechny, ale po posledním
kole musí zůstat v turnaji sám.
Příklady: pro N = 500 a K = 3 je řešením 437, 55, 7, pro
N = 15 a K = 8 je to 3, 3, 2, 2, 1, 1, 1, 1.
Řešení
Pojďme si povědět ještě něco o programovacích jazycích obecně – hlavně o tom,
jaké jsou jejich druhy. Mezi nejvýraznější patří rozdělení na nízkoúrovňové
(více se blížící strojovému kódu, tedy jazyku počítače) a vyšší (bližší
člověku).
Zástupcem první skupiny je např. assembler. Dalších nízkoúrovňových není tolik,
pokud nebudeme hledět na odlišnosti dané hardwarem, a programátoři se s nimi
setkávají málo, většina vývoje i dělení se proto týká jen vyšších jazyků.
Při procházení historických jazyků jsme už nakousli dělení na jazyky
imperativní (program je posloupnost příkazů) a deklarativní (zapisuje se, co se
má spočítat, a nezáleží tolik na tom, jak). Známými deklarativními jazyky jsou
LISP, Haskell (oba funkcionální) a Prolog (logické programování).
Všechny imperativní jazyky jsou dnes procedurální, ačkoliv zprvu neobsahovaly
podprogramy, neboli procedury či funkce. Často se proto musel používat příkaz
goto (skok na jiné místo v programu), což vedlo k nepřehlednosti. Dnes už
se goto téměř nepoužívá, i když v programovacích jazycích často bývá.
O objektový přístup obohatil programování jazyk Simula určený pro diskrétní
simulace. Obsahuje objekty, třídy, dědičnost, a dokonce i garbage
collection (automatickou správu paměti).
Z hlediska rychlosti provádění kódu a pohodlnosti při psaní jsou dvěma
protipóly jazyky kompilované (kompilátorem převáděné do strojového kódu) a
interpretované (program, jemuž se říká interpretr, čte kód a rovnou ho
provádí, což bývá pomalejší).
Pokud vám na předchozím odstavci něco nesedí, pak je to dobře. Jazyk je totiž
jen forma zápisu, a tak existují interpretry jazyka C, typického zástupce
kompilovaných, a naopak kompilátory pro skriptovací jazyk Python.
24-1-4 Složitá složitost (7 bodů)
 Ačkoliv si v této sérii vyprávíme o programovacích jazycích, při řešení úloh
KSPčka nám o ně obvykle moc nejde – víc než použitý jazyk, ať už kompilovaný
nebo interpretovaný, nás zajímá nás tzv. asymptotická časová složitost. Ta je zcela
nezávislá na jazyce a umožňuje rozlišit, jak je který algoritmus rychlý, aniž
bychom ho museli spouštět na skutečném počítači.
Ačkoliv si v této sérii vyprávíme o programovacích jazycích, při řešení úloh
KSPčka nám o ně obvykle moc nejde – víc než použitý jazyk, ať už kompilovaný
nebo interpretovaný, nás zajímá nás tzv. asymptotická časová složitost. Ta je zcela
nezávislá na jazyce a umožňuje rozlišit, jak je který algoritmus rychlý, aniž
bychom ho museli spouštět na skutečném počítači.
Více se o složitosti dozvíte z kuchařky na konci letáku. Její přečtení
doporučujeme před řešením této úlohy všem, kdo ještě nikdy složitost neurčovali
nebo jim stále přijde poněkud složitá. Ostatním může kuchařka sloužit pro osvěžení
znalostí před novým ročníkem.
V této úloze jsme si pro vás připravili pseudokód (zjednodušený kód) algoritmu.
Jeho úkolem je setřídit zadané pole čísel, čili jeho prvky přerovnat do vzestupného pořadí.
Vaším úkolem pak je určit časovou a paměťovou složitost tohoto algoritmu a zdůvodnit,
proč tomu tak je. Zajímá nás složitost v nejhorším případě.
Ještě poznámka pro pořádek: pole indexujeme od 1 a parametr n říká, kolik
v něm je uloženo prvků.
Funkce Setřiď(pole, n):
odm = odmocnina z n zaokrouhlená dolů
i = 1
Dokud i <= n:
změna = true
Dokud změna je true:
změna = false
Pro j od i do min(i+odm-2, n-1):
Jestliže pole[j] > pole[j+1]:
Prohoď pole[j] a pole[j+1]
změna = true
i = i + odm
vysl = vytvoř pole délky n
zač = vytvoř pole délky odm+1
Do všech prvků pole zač vlož 0
Pro i od 1 do n:
vysl[i] = nekonečno
minIndex = 1
j = 1
k = 1
Dokud j <= n:
Jestliže zač[k] < odm a j+zač[k] <= n:
a = pole[j + zač[k]]
Jestliže a < vysl[i]:
vysl[i] = a
minIndex = k
j = j + odm
k = k + 1
zač[minIndex] = zač[minIndex] + 1
Vrať vysl
Řešení
Zvláštní kategorii tvoří výukové jazyky, snažící se být co nejjednoduššími a
zároveň poutavými pro děti. Někdy jsou v nich textové příkazy nahrazeny
ikonkami, z nichž se vytváří program metodou táhni a pusť.
V Logu, starém již přes 40 let, se ovládá želva, která chodí po ploše, a když
spustí ocásek, kreslí za sebou stopu. Tomuto způsobu kreslení se dodnes říká
želví grafika.
24-1-5 Razítková grafika (12 bodů)
 Představme si vytváření grafiky trochu podobné želví, ale s jedinou operací –
otisk čtvercového razítka. Kreslit budeme na klasickou bitmapu (čtvercovou síť
pixelů) jedinou barvou, například černou na bílé pozadí.
Představme si vytváření grafiky trochu podobné želví, ale s jedinou operací –
otisk čtvercového razítka. Kreslit budeme na klasickou bitmapu (čtvercovou síť
pixelů) jedinou barvou, například černou na bílé pozadí.
Dostali jste černobílý obrázek o rozměrech N×M pixelů a vaším úkolem je
určit, pomocí jakého největšího razítka mohl být vytvořen. Žádný pixel nesmí
být orazítkován dvakrát.
Na obrázku je příklad vstupní bitmapy. Největší razítko, kterým se dá vytvořit,
má velikost 1 pixel, razítkem se 2 pixely by nešel nakreslit čtverec 3×3
vlevo dole.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Dalším jazykem pro děti je v ČR vytvořený Karel (pojmenovaný po Karlu Čapkovi), v němž se na
čtvercové síti ovládá robot. Domácího původu je i Baltík obsahující postavičku
čaroděje, který chodí po ploše a čaruje na políčka obrázky.
24-1-6 V bludišti s krumpáčem (9 bodů)
V Baltíkovi i v Karlovi je typickou úlohou pro začátečníky procházení bludiště.
Postavička chodí po čtvercové (popř. obdélníkové) síti, musí se vyhýbat zdem,
ale občas se může rozhodnout nějakou zbourat.
Máte mapu velkého bludiště na čtvercové síti s rozměry N×M. Políčko je buďto
prázdné, nebo je na něm zeď. Úkolem je najít pro postavičku nejrychlejší cestu
od vchodu do bludiště k východu (je tam jen jeden) s tím, že zbourání zdi stojí
stejně času jako ujít K - 1 políček (takže políčko se zdí postavička projde
celkově za stejný čas jako K prázdných).
Pro jednoduchost stačí vypsat dobu na projití nalezené trasy. Můžete také předpokládat,
že K je nejvýše 10.
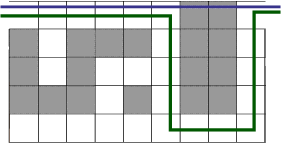
Příklad bludiště vidíte níže na obrázku. Pro K menší než 5 se vyplatí probourat
dvě zdi, pro K větší než 5 je lepší zdi obejít a pro K = 5 jsou stejně dobré
obě cesty.
Řešení
Léta vývoje programovacích jazyků přinesla i mnohé plody, jež jsou hezké,
zajímavé či alespoň vtipné, leč v praxi naprosto nepoužitelné. Jedním
z nejznámějších je Brainfuck, který si své jméno skutečně zasluhuje.
Běh programu v něm si lze představit jako operace nad polem bytů, přičemž je
k dispozici jen jeden ukazatel na aktivní buňku, s níž jedinou lze pracovat bez
změny ukazatele. K tomu všemu stačí 8 instrukcí reprezentovaných 8 znaky,
ostatní se ignorují.
ZOO takovýchto esoterických jazyků je opravdu pestrá. Obsahuje nejen příbuzné
Brainfucku (např. Ook!), ale třeba i Malbolge, který se snaží, aby bylo programování
v něm co nejobtížnější, INTERCAL, v němž je nutno mimo jiné o provedení příkazu prosit,
avšak ne moc, a Whitespace, který využívá jen znaků mezera, tabulátor a nová řádka.
Jelikož má Brainfuck stejnou výpočetní sílu jako jiné běžné jazyky (populárně
řečeno), jako demonstraci užitečnosti uveďme jazyk HQ9+ se 4 instrukcemi
pokrývajícími typické testovací úlohy pro jazyky, leč nic jiného:
h – vypíše „Hello, world!“,q – zobrazí zdrojový kód programu,9 – vypíše text k písničce „99 Bottles of Beer on the Wall“ (ano, má 100 slok),+ – zvýší o 1 hodnotu akumulátoru.
Že programování je umění (dokonce abstraktní) a psát není potřeba, dokazuje Piet,
pojmenovaný po holandském malíři Pietu Mondrianovi. Některá jeho abstraktní díla vypadají skoro stejně
jako programy v Pietu, reprezentované bitmapou s maximálně 20 barvami.
Pokud vás netradiční programování zaujalo, pěknou sbírku roztodivných jazyků najdete na
specializované wiki.
Jak bude vypadat vývoj jazyků v budoucnosti? Někteří tvrdí, že nic nového,
převratného do 10 let nepřijde a na špičce se udrží stávající jazyky, které se
budou jen pomalu vyvíjet a dále přejímat prvky z funkcionálních jazyků. Třeba
nás ale někdo překvapí!
Jedním z nových trendů, jež se nyní rychle rozvíjí, je paralelismus,
vycházející z myšlenky rozdělit dlouho trvající výpočty mezi několik procesorů
nebo počítačů. Třeba se dají takto prolamovat některé jednodušší šifry.
24-1-7 Distribuované výpočty (10 bodů)
Firma Hack & Crack vlastní N (tedy mnoho) počítačů vzájemně propojených
mezi sebou (ne nutně každý s každým). Rozhodla se, že prolomí šifru americké armády, a
na výpočet nasadila veškeré síly.
Uběhlo pár dní a programátoři z hrůzou zjistili, že je ve výpočtu chyba a musí
se přerušit. Postupně tedy vypínají počítače, chtějí však, aby se v každém
okamžiku mohly všechny běžící počítače spolu domluvit (tj. mezi každými dvěma
lze přes nějaké jiné poslat zprávu).
Pomozte jim najít pořadí, v němž mají vypínat počítače (očíslované od 1 do
N). Na vstupu kromě N dostanete i seznam dvojic kabelem propojených
počítačů (propojení je obousměrné).
Můžete předpokládat, že na začátku lze poslat zprávu mezi každými dvěma
počítači. Je-li řešení více, stačí najít jen jedno.
Příklad: ve firmě je 7 počítačů a propojené jsou 1-2, 1-3, 2-3, 3-4, 3-5,
3-6, 3-7, 5-6, 6-7. Řešením je například vypínat v pořadí 4, 5, 7, 6, 3,
1, 2 nebo 2, 5, 6, 7, 4, 1, 3 a nebo mnoha jinými způsoby.
Řešení
Ve vzdálené budoucnosti by se klidně mohlo programovat v angličtině nebo i
v češtině. Hello world by vypadal třeba takto:
Vypiš „Dobrou noc, světe!“ (bez uvozovek)
a skonči.
Co byste říkali na takovýto program?
Vyřeš všechny úlohy z 1. série.
Zapiš jejich řešení po jednom do PDF.
Odevzdej řešení přes web KSP.
Zatím jediným alespoň trochu funkčním překladačem češtiny se zdají být čeští
programátoři. Dokážete napsat kompilátor pro počítač, který bude dobrý alespoň
jako člověk, co neprogramuje?
Povídání o jazycích sepsal Pavel Veselý.
24-1-8 Pojďte pane, budeme si hrát (14 bodů)
 Letos se bude seminářem jako červená nit proplétat seriál o hrách a jejich
matematickém a výpočetním řešení. To důležité, co si z něj můžete odnést,
je přehled o tom, jakým způsobem současné počítače získávají náskok před
lidským rozumem a v jakém vztahu mohou koexistovat chytrá pozorování
a hrubá výpočetní síla.
Letos se bude seminářem jako červená nit proplétat seriál o hrách a jejich
matematickém a výpočetním řešení. To důležité, co si z něj můžete odnést,
je přehled o tom, jakým způsobem současné počítače získávají náskok před
lidským rozumem a v jakém vztahu mohou koexistovat chytrá pozorování
a hrubá výpočetní síla.
Definovat si, co znamená hra, zní nanejvýš otravně, ale je to pojem tak
obecný, že s nějakým vymezením začít musíme. Nebo od nás čekáte, že budeme
studovat, jak počítačem řešit schovávanou?
- Mějme právě dva hráče.
- Hráči se střídají v tazích.
- Každý tah se vybírá z konečné sady možností. Piškvorky tedy budeme nazývat
hrou jen pro předem omezenou velikost čtverečkovaného papíru.
- Oba hráči znají celou informaci o hře, takže žádný z nich neskrývá karty.
- Průběh hry je závislý pouze na tazích hráčů, takže neexistuje náhoda a nehází se kostkou.
Můžeme začít!
Matematika funguje
Přestože víme, že počítače jsou v šachách lepší než lidé, neplatí, že by šachy
byly vyřešená hra – neví se totiž, že by nějaká strategie zaručovala vítězství
proti libovolnému oponentovi.
Existují hry, jako je anglická dáma, které vyřešené jsou, ale tak nějak
„suše“. Máme v nich strategii, která zaručí, že nikdy neprohrajeme, nejde
však o elegantní matematický nápad, jako spíš o velmi dlouhý seznam (či spíš
strom) pravidel.
Vzhledem k tomu, jak arbitrární jsou pravidla oblíbených her, nedá se ani čekat,
že by pro ně někdo někdy takový hezký matematický nápad našel. Existují ale hry
matematické. Říká se jim tak, protože mají pravidla formulovatelná v řeči
matematiky tak snadno či příznivě, že očekáváme, že by krásná řešení mít mohly.
Jednu takovou matematickou hru si ukážeme. Překvapivě, tuto hru lidé občas stále
hrají – a hráli dlouho předtím, než byla jako důležitá matematická hra
rozpoznána.
Mějme tři hromádky nerozlišitelných žetonů. Hráči se střídají v tom, že z jedné
hromádky seberou a zahodí libovolné nenulové množství žetonů. Prohrává ten, na kterého
žádný žeton nezbude.
Když si tuto hru zkusíte zahrát, zjistíte, že úplně triviální není. Má však
elegantní matematické řešení, které nám dává rychlou metodu, jak určit, jestli
má hráč na tahu zajištěnou výhru a pokud ano, jak by měl táhnout.
Zjednodušme si situaci a redukujme počet hromádek na dvě. Jak hrát tuto hru je
nasnadě, ale rozmyslete si to. Pokušení číst dál, aniž byste řešení našli, je
třeba odolat, protože spoilery v matematice hrají stejně zápornou roli, jako
spoilery u filmů s důležitým zvratem.
Takovou hru má vyhranou první hráč na tahu právě tehdy, je-li na hromádkách
rozdílný počet žetonů. Táhnout bude tak, že sebere z početnější hromádky tolik
žetonů, aby počet dorovnal. Protivníkovi tak nezbude, než rovnost opět porušit.
To se bude opakovat do té doby, než hráč, co dostává situaci s rozdílným počtem
žetonů, dostane jednu z hromádek prázdnou – vyhraje pak sebráním celé druhé
hromádky. Hráči, co dostává situaci s tím samým počtem žetonů, se něco takového
evidentně stát nemůže – jedním tahem nikdy dvě neprázdné hromádky neodstraní.
Dobře tedy! Při třech hromádkách budeme hledat podobné smutné stavy hry,
- do nějakého z nich bude mít jeden hráč možnost druhého vždy uvrhnout z každého
stavu, který smutný není,
- které budou zahrnovat prázdnou (prohrávací) pozici,
- a všechny tahy ze smutných pozic vedou do pozic, které smutné nejsou.
Řešením je vyjádřit si počty žetonů na hromádkách jako binární čísla a provést
po číslicích jejich xor (ten jsme milou náhodou zavedli už v úloze 24-1-1).
Stav jako smutný označíme tehdy, vyjde-li nám nula.
Úkol 1 [5b]
Ověřte, že taková definice splňuje tři požadavky, které jsme měli.
Uvědomte si, že tímto pozorováním získáme strategii, jak hru se třemi hromádkami
vyhrát pokaždé, když nejsme ve smutném stavu, kdy nad námi naopak bude moci vždy
vyhrát protivník.
Můžeme si také všimnout, že popsaná strategie pro dvě hromádky je ve skutečnosti
ten samý postup. Ještě zajímavější je, že nám strategie funguje pro libovolný
konečný počet hromádek!
Generování možných tahů
V druhé části seriálu se zaměříme na hry, které efektivně vyřešit neumíme.
Zřejmě se nebudeme snažit, aby za nás počítač pochopil, jaké strategie jsou
dobré, protože počítač je v chápání opravdu nemožný. Co mu naopak velmi jde, je
procházení všech možností.
Máme výchozí situaci a chceme udělat první půltah (půltah je zahrání jednoho
hráče a tah je půltah hráče společně s následujícím půltahem protihráče). Můžeme
si spočítat, jak bude vypadat deska po každém z možných půltahů, a uvažovat
nad tím, je-li to pro nás dobrá pozice. Asi ale tušíte, že z toho mnoho
nezjistíme. Potřebujeme rozmýšlet na více tahů dopředu.
Dobře. Nagenerujeme všechny možné situace desky po 8 půltazích. Třeba rekurzivně:
Funkce generuj (pozice, hloubka, kdo je na tahu):
Pokud je hloubka=0 nebo je pozice vyhrávající či prohrávající:
Vypiš pozice.
Pro všechny možné tahy t hráče, který je na tahu, z pozice:
generuj (pozice po tahu t, hloubka-1, druhý hráč)
Co nevidíme, je tam pozice, ve které jsme vyhráli!
Slavnostně si vybavíme, jaká sekvence půltahů vede do této pozice a zahrajeme
první z nich. Ale co se nestalo, protivník se svou brzkou záhubou nesouhlasí a
hraje jinam, do pozice, která pro nás nevypadá dobře.
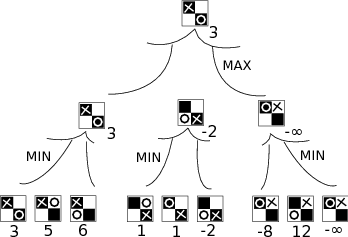
Minimax aneb „O tom nerozhoduješ!“
Byli jsme nerozvážní. Nemůžeme si jen tak vybrat, kam se dostat – musíme počítat
s tím, že naše možnost ovlivňovat hru je jaksi poloviční a navíc že protivník je
inteligentní a druhá polovina tahů povede proti našemu zájmu.
Nalezení prostého maxima z nalezených pozic se tedy vyvarujeme. Využijeme
zvoleného rekurzivního způsobu generování tahů a budeme si vracet maxima tam,
kde máme volbu, a minima tam, kde volbu nemáme a kde očekáváme, že půjde
protihráč proti nám.
Funkce generuj (pozice, hloubka, kdo je na tahu):
Pokud je hloubka=0 nebo je pozice vyhrávající či prohrávající:
Vrať pozice.
Zavedeme prázdný seznam možnosti.
Pro všechny možné tahy t hráče, který je na tahu, z pozice:
Přidej do možnosti hodnotu
generuj (pozice po tahu t, hloubka-1, druhý hráč).
Pokud jsem na tahu já:
Vrať nejlépe ohodnocenou pozici ze seznamu možnosti.
Jinak:
Vrať nejhůře ohodnocenou pozici ze seznamu možnosti.
Tomuto algoritmu se obvykle říká minimax.
Abychom ho mohli implementovat, potřebujeme počítači vysvětlit, jak poznat,
která situace je pro nás lepší, než jiná. Obvyklou volbou je napsat funkci,
která pozici přiřadí hodnotu z množiny reálných čísel obohacených o hodnoty
+∞ a -∞, které slouží jako indikace „výhry“ a „prohry“. Vysoká
kladná čísla budou znamenat, že je pozice velmi dobrá, záporná, že je pozice
slabá.
Kvality této ohodnocovací funkce budou do značné míry ovlivňovat kvalitu
výsledného algoritmu. Uvědomme si, že minimax zaručuje, že se dostaneme do
relativně dobře ohodnocené situace, pokud si ale ohodnocovací funkce spletla
dobrý skutečný stav věcí se špatným, prohráváme.
Pokud bychom mohli minimax spustit neomezeně půltahů hluboko, do konce každé
hry, stačilo by, aby ohodnocovací funkce poznala vítězství a prohru, a náš
algoritmus by hrál nejlépe možně – pokud by mohl vyhrát, vyhrál by. To však
není realistické očekávat – s prohledáváním o každý půltah hlouběji se běh
násobně zpomalí.
Ohodnocovací funkce může pozici zkoumat podrobně a strávit nad tím hodně času,
minimax ale potom nestihne postoupit do tak hluboké úrovně, jako kdyby bylo
ohodnocování pozic povrchní a nespolehlivé. To, jak pečlivé zkoumání stojí za to
zvolit, záleží především na povaze řešené hry.
Druhá důležitá funkce generuje možné půltahy. Ve většině her je jen několik málo
půltahů rozumných a u části nerozumných půltahů to můžeme algoritmicky rozeznat
ihned, aniž bychom pouštěli minimax.
Kupříkladu v piškvorkách nemá cenu hrát příliš daleko od bojiště. Nemůžeme si
být jisti, jestli některá optimální strategie s takovým dalekým tahem nepočítá,
ale ani ve hrách velmi dobrých hráčů se nic takového nevyskytuje a my si tak jen
na základě tohoto pozorování můžeme dovolit násobně zmenšit počet vygenerovaných
tahů.
Dobře zvolit, které situace z generátoru pouštět a které ne, je důležité
rozhodnutí, protože jím omezujeme, jak moc se nám bude strom volání větvit,
tedy (opět) jak hluboko budeme moci propočítávat.
Úkol 2 [7b]
Napište ohodnocovací funkci a generátor možných tahů pro hru
šestvorky na desce 15×15. Tato hra se od běžných piškvorek liší ve dvou
„drobnostech“:
- Vyhrává linie šesti, ne pěti značek.
- Hráči pokládají hned dvě své značky ve svém půltahu místo jedné, s výjimkou
úplně prvního tahu začínajícího hráče, při kterém se pokládá značka toliko
jedna. Je to hezké pravidlo, protože činí hru vyrovnanější.
Od 21. srpna (tedy od skončení nulté série) do uzávěrky série této bude na
stránkách semináře aréna, ve které se budou vaše funkce zasazené do minimaxového
algoritmu bít. Dozvíte se tam i technické detaily. Zde uvádíme jen,
- že čas na vyhodnocení jednoho tahu bude zhruba deset sekund,
- že pozici budete dostávat jako obyčejné dvojrozměrné pole a že žádné jiné
informace nebudete smět použít (nepůjde si ukládat data mezi ohodnoceními)
- a že programovacím jazykem bude Python.
S účastí není potřeba zvlášť spěchat, protože doba, po kterou se bude algoritmus
soutěže účastnit, závěrečné vyhodnocení sama od sebe neovlivní. Přirozeně je
dobrý nápad zkusit si včas, jak si na tom stojíte, a tak se v případě
neuspokojivého výsledku motivovat k další práci.
Všechna řešení, která překonají námi připravenou dvojici funkcí, dostanou sedm
bodů. Zbylé dva body rozdělíme podle umístění v tabulce.
Lukáš Lánský
Řešení
 Představte si, že jste s kolegou z práce dostali obrovskou hromadu hardwarových
součástek, přičemž každá má nějakou cenu danou přirozeným číslem. Chcete je
rozdělit na dvě části, aby byl v obou stejný součet cen.
Představte si, že jste s kolegou z práce dostali obrovskou hromadu hardwarových
součástek, přičemž každá má nějakou cenu danou přirozeným číslem. Chcete je
rozdělit na dvě části, aby byl v obou stejný součet cen. Ačkoliv si v této sérii vyprávíme o programovacích jazycích, při řešení úloh
KSPčka nám o ně obvykle moc nejde – víc než použitý jazyk, ať už kompilovaný
nebo interpretovaný, nás zajímá nás tzv. asymptotická časová složitost. Ta je zcela
nezávislá na jazyce a umožňuje rozlišit, jak je který algoritmus rychlý, aniž
bychom ho museli spouštět na skutečném počítači.
Ačkoliv si v této sérii vyprávíme o programovacích jazycích, při řešení úloh
KSPčka nám o ně obvykle moc nejde – víc než použitý jazyk, ať už kompilovaný
nebo interpretovaný, nás zajímá nás tzv. asymptotická časová složitost. Ta je zcela
nezávislá na jazyce a umožňuje rozlišit, jak je který algoritmus rychlý, aniž
bychom ho museli spouštět na skutečném počítači. Představme si vytváření grafiky trochu podobné želví, ale s jedinou operací –
otisk čtvercového razítka. Kreslit budeme na klasickou bitmapu (čtvercovou síť
pixelů) jedinou barvou, například černou na bílé pozadí.
Představme si vytváření grafiky trochu podobné želví, ale s jedinou operací –
otisk čtvercového razítka. Kreslit budeme na klasickou bitmapu (čtvercovou síť
pixelů) jedinou barvou, například černou na bílé pozadí.
 Letos se bude seminářem jako červená nit proplétat seriál o hrách a jejich
matematickém a výpočetním řešení. To důležité, co si z něj můžete odnést,
je přehled o tom, jakým způsobem současné počítače získávají náskok před
lidským rozumem a v jakém vztahu mohou koexistovat chytrá pozorování
a hrubá výpočetní síla.
Letos se bude seminářem jako červená nit proplétat seriál o hrách a jejich
matematickém a výpočetním řešení. To důležité, co si z něj můžete odnést,
je přehled o tom, jakým způsobem současné počítače získávají náskok před
lidským rozumem a v jakém vztahu mohou koexistovat chytrá pozorování
a hrubá výpočetní síla.