Druhá série dvacátého pátého ročníku KSP
Celý leták v PDF.
Zadání úloh
„Újezd. Příští zastávka: Hellichova.“
No jo, tahle hlášení bych mohla odříkávat nazpaměť. Ne že bych si za těch pár
let, co v Praze žiju, stihla zapamatovat všechny linky MHD, ale úseky některých
z nich ano.
Dav turistů, mířících nejspíš na petřínskou lanovku, se vyhrne z tramvaje. Hned
se tu aspoň dá trochu dýchat. Někdy by se hodilo vědět, kde se má člověk
připravit na největší davy.
25-2-1 Vytíženost dopravy (13 bodů)
Pokud si představíme, že zastávky jsou vrcholy grafu a spoje představují hrany
mezi nimi, potom dopravní síť tvoří strom. Hrany jsou ohodnocené očekávaným
počtem cestujících.
Navrhněte datovou strukturu, která se vybuduje pro zadaný
strom a následně bude umět co nejrychleji odpovídat, ve kterém úseku (na které
hraně) cesty z vrcholu X do vrcholu Y pocestuje nejvíce lidí. Počítejte s tím,
že počet dotazů bude řádově odpovídat počtu vrcholů.
 Lehčí varianta (za 7 bodů): Řešte stejnou úlohu za předpokladu, že grafem
představujícím dopravní síť je cesta.
Lehčí varianta (za 7 bodů): Řešte stejnou úlohu za předpokladu, že grafem
představujícím dopravní síť je cesta.
Řešení
Konečně dorážíme na Hellichovu. Ani nečekám na další hlášení a vystupuju. Teď
už jen pár uliček a japonský velvyslanec pan Yamada se může těšit na milou
návštěvu. Jemu možná tak milá připadat nebude, ale… vaše články se nedostanou
na titulní stránky novin proto, že se lidí ptáte jen na milé věci.
Cestou kolem muzea hudby si všímám hezky upravené zahrady, a hlavně chlapíků,
co ji právě sečou. Pořád se střídají u sekačky. Skoro to vypadá, že hrají
nějakou hru.
25-2-2 Sekání trávy podruhé (11 bodů)
Mějme zahradu tvořenou několika obdélníky ve čtvercové síti. Zahrada je
souvislá. Jednotlivé obdélníky spolu sousedí, ale nepřekrývají se. Každý
obdélník má sudý obsah.
Na začátku stojí sekačka na libovolném políčku. Dva hráči se pravidelně
střídají, každý vždy popojede se sekačkou o jedno políčko. Benzín je v dnešní
době drahý, a proto nesmí být žádné políčko posekáno vícekrát. Ten hráč, který jako
první nemá kam sekačkou pohnout, prohrál a musí ji po dosekání uklidit.
Rozhodněte, pro kterého hráče existuje výherní strategie, a popište ji. Tedy
zjistěte, jestli vyhraje ten, kdo pohne se sekačkou jako první, nebo ten, kdo
s ní pohne jako druhý. Pro tohoto hráče popište, jak má táhnout, aby mu žádné
protitahy jeho soupeře nezkazily výhru.
Na obrázku je jeden z možných tvarů zahrady. Úlohu řešte obecně pro všechny
tvary zahrady splňující podmínky zadání.
Řešení
Na chvilku jsem se u sledování sekání zapomněla, ale opět vyrážím dál. Po
chvilce se dostávám na místo určení. A koho to nevidím, to bych si snad ani
nemohla naplánovat – pan Yamada osobně. Přidávám do kroku.
„Ohayou gozaimasu, Yamada-sama!“ zastupuju muži cestu, zatímco si nenápadně
zapínám ukrytý diktafon. Prvotní překvapení ve tváři pana Yamady střídá jasný
výraz nespokojenosti, tím se ovšem nenechávám zastrašit. Mluvím o nedávných
případech, ptám se ho na jeho názor. Mluvím o mafii a chci po něm vyjádření.
Odpovědi jsou všechny jenom takové ty diplomatické frázičky, ale jsem si jistá,
že tenhle člověk ví víc, než přiznává. Najednou pan Yamada sahá po telefonu a
s omluvou odchází o kus dál. Zaslechnu jen slova „… zase tady“ a „udělej
s ní něco“, kupodivu mluví česky. Začínám tušit problémy.
A taky že jo! Neuplynulo snad ani pět minut a přihnal se sem nějaký policista.
Že tohle nesmím, že musím odejít, blá blá.
Je čas použít mou úžasnou výmluvu. „Promiňte, já si jen chtěla nechat
poradit s touhle japonskou kalkulačkou,“ vytahuju svoji starou kalkulačku
značky Yamaha. „Má jeden zajímavý mód.“
25-2-3 Doplňování operátorů (6 bodů)
 Máme zadaná celá čísla a chceme mezi ně doplnit znaménka plus + nebo krát * tak, aby
výsledek vzniklého výrazu byl co největší. Jak to máme udělat?
Máme zadaná celá čísla a chceme mezi ně doplnit znaménka plus + nebo krát * tak, aby
výsledek vzniklého výrazu byl co největší. Jak to máme udělat?
Příklad:
Pro čísla 6 2 1 3 0 je nejvýhodnější doplnění
6 * 2 * 1 * 3 + 0 = 36.
Řešení
Evidentně byl úkol příliš jednoduchý. Hlavně mě ten policista zdržel natolik,
že milý pan velvyslanec pláchl. Pro teď bude asi rozumnější zmizet a vrátit se
sem jindy. Raději se půjdu někam projít.
Moje kroky mě dovedly až na Kampu. A o kus dál, k menšímu japonskému chlapci.
Působí ztraceně, radši ověřím situaci.
„Ooi. Hitoribocchi desu. Naze.“ ptám se. Chlapec se na mě podíval a úplně se
mu rozzářily oči.
Po chvilce už vím, že se jmenuje Tanaka, zatoulal se své skupince a že snad
trefí tam, kde se mají sejít. Samozřejmě ho doprovodím, potřebuje to… a kdo
ví, třeba se od jeho skupinky ještě dozvím něco zajímavého.
Z Tanakova výrazu vyčtu, že bychom měli být na místě, a vzápětí lapám po dechu.
Mafiáni! Lidi před námi jsou určitě mafiáni uprostřed akce. Když děláte
novinařinu dost dlouho, na některé věci prostě máte čuch, a tohle k nim patří.
Chvíli sleduju, jak jsou zorganizovaní.
25-2-4 Organizace vykládky (13 bodů)
 Základem organizovanosti je vybrání dobrého místa pro zastavení
dodávky. Mafiáni se kolem ní pak rozestaví v pomyslné čtvercové síti a
předávají si zboží, které se má dopravit na jednotlivá místa. Je
žádoucí, aby počet mafiánů potřebných na vyložení všeho zboží byl co
nejmenší. Pohyb mafiánů po čtvercové síti odpovídá pohybu krále po
šachovnici.
Základem organizovanosti je vybrání dobrého místa pro zastavení
dodávky. Mafiáni se kolem ní pak rozestaví v pomyslné čtvercové síti a
předávají si zboží, které se má dopravit na jednotlivá místa. Je
žádoucí, aby počet mafiánů potřebných na vyložení všeho zboží byl co
nejmenší. Pohyb mafiánů po čtvercové síti odpovídá pohybu krále po
šachovnici.
Formálněji řečeno, mějme N bodů v rovině, používejme maximovou metriku
(právě ta odpovídá minimálnímu počtu kroků šachového krále mezi dvěma
poli šachovnice). Hledáme bod ze zadaných, pro který platí, že součet
vzdáleností od všech ostatních bodů je pro něj nejmenší.
Maximová metrika funguje v rovině tak, že vzdálenosti dvou bodů odpovídá větší
z rozdílů jejich souřadnic. Tedy d((x1,y1), (x2,y2)) = max{|x1-x2|, |y1-y2|}.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Najednou se objeví blesk z Tanakova foťáku. A do háje! Všichni si nás
samozřejmě všimli.
Chytám Tanaku za ruku a rozbíhám se s ním pryč. Kdyby nás chytili, mohlo by to
být hodně špatné. Najednou se mi Tanaka vytrhl. Běží doprava. Nejsem si jistá,
co má v plánu, ale odbočuju doleva. Máme tak větší šance a on se snad znovu
neztratí. Ani nenechá chytit.
Z nějakého důvodu, možná jak jsme se od sebe tak odtrhli, mi ale vyletěl
z brašny blok s poznámkami a vysypaly se z něj jednotlivé papíry!
To mi tak chybělo… potřebuju je posbírat, a to hezky rychle.
25-2-5 Sbírání papírů (8 bodů)
Novinářce se na cestu rozsypaly papíry. Představme si cestu jako čtvercovou síť
M×N, kde přesun mezi dvěma políčky odpovídá jednomu kroku a není povoleno
přesouvání šikmo. Na některá pole se vysypaly jednotlivé papíry.
Novinářka se nemůže vracet zpět (řekněme dolů), může jen vpřed (nahoru),
doprava a doleva. Zároveň potřebuje posbírat všechny papíry na co nejmenší
počet kroků. Navrhněte algoritmus, který jí poradí, jak se má pohybovat. Na
začátku stojí novinářka v levém dolním rohu.
Příklad:
(políčko s papírem je 1, bez papíru 0)
0 1 0 0
0 1 0 1
0 0 1 0
Optimální řešení je například RRURLLU.
 Lehčí varianta (za 3 body): Řešte úlohu pro oblast širokou právě 3 políčka, tedy pro
čtvercovou síť rozměru 3×N.
Lehčí varianta (za 3 body): Řešte úlohu pro oblast širokou právě 3 políčka, tedy pro
čtvercovou síť rozměru 3×N.
Řešení
S papíry v náručí utíkám dál, dokud se mi nepovede setřást i posledního
mafiána. Těžce oddechuju. Vůbec jsem nevnímala, kam běžím, ale to vyřeším
později. Tohle bude úžasný článek. Škoda jenom, že nemám ty fotky, co nafotil
Tanaka. Ale žiju, to je možná hlavní.
Sahám do brašny pro mobil, abych zavolala Jitce. Moment, tady je něco špatně!
Chvíli zoufale přehrabuju brašnu, než si připustím, že má peněženka v ní prostě
není. Jenže ráno jsem ji určitě měla. Musela jsem ji vytratit při tom zběsilém
útěku. Co teď?
Zpátky, přímo do náruče mafiánů, se mi tedy nechce. Raději vyrážím po okolí se
zoufalou nadějí, že se peněženka někde zázračně objeví.
A dneska se zázraky podle všeho dějí. Kluk, kterého vidím, totiž není nikdo
jiný než Tanaka, a věc, kterou drží ve své ruce, není nic jiného než má
peněženka! A …, počkat, to je ten otrava z rána, co mě odháněl od ambasády!
Co se to tam vlastně děje? Tanaka mává mou peněženkou a Otrava mu bere foťák…
Ha, foťák! Kdybych se dostala k fotkám, byl by materiál pro článek už naprosto
dokonalý.
Dojdu k těm dvěma blíž. Tanaka je tak zaražený, že si vůbec nevšímá, když mu
z ruky vytáhnu svou peněženku. Otrava si toho ale všiml a hned po mně vyjel.
Bráním se, že peněženka je moje, že v ní jsou doklady, podle kterých mě může
zkontrolovat.
S nedůvěřivým pohledem mi bere peněženku. Nijak zásadně se nebráním.
„Nechcete podržet ten foťák, ať to můžete líp zkontrolovat?“ ptám se.
„Hm… jo, díky,“ zabručí Otrava a podá mi foťák.
Jo! Když děláte novinařinu dost dlouho, naučíte se taky dost rychle vytahovat
paměťovky z foťáků. A dost nenápadně.
Takže když mi pan policista o chvíli později s náležitými omluvami a domluvami
podává peněženku zpět, bydlí už paměťovka z Tanakova foťáku v mé brašně.
Spokojeně mizím přímo do redakce.
Tam mě vítají zprávy o optimalizaci, či co to má být.
25-2-6 Optimalizace v redakci (9 bodů)
 Novinový článek se může nacházet v mnoha různých stavech a mezi každými dvěma
z nich ho může přesouvat nejvýše jeden redaktor. Každému takovému redaktorovi
se ale platí, a šéfredaktoři se rozhodli snížit výdaje. Chtějí tedy některé
redaktory propustit, aby součet platů těch zbylých byl co nejmenší.
Novinový článek se může nacházet v mnoha různých stavech a mezi každými dvěma
z nich ho může přesouvat nejvýše jeden redaktor. Každému takovému redaktorovi
se ale platí, a šéfredaktoři se rozhodli snížit výdaje. Chtějí tedy některé
redaktory propustit, aby součet platů těch zbylých byl co nejmenší.
Je ovšem třeba zajistit, že se článek stále bude moci dostat z libovolného
stavu do libovolného jiného. Zjistěte, kteří redaktoři se nemusí trápit, kteří
si mají začít hledat novou práci a kteří by měli vyrazit koupit svým nadřízeným
dobrou bonboniéru.
Formálněji řečeno, nalezněte algoritmus, který pro každou hranu neorientovaného
ohodnoceného grafu (váhy více hran mohou být stejné) rozhodne, zda ta hrana
leží v každé minimální kostře grafu, žádné minimální kostře, nebo v některých
minimálních kostrách. Připomeňme, že o minimálních kostrách píšeme v kuchařce.
Příklad:
V následujícím grafu jsou tučně vyznačeny hrany, které leží ve všech
minimálních kostrách, tence hrany, které leží v některých, a čárkovaně hrany,
které neleží v žádné minimální kostře.
Řešení
S potěšením zjišťuju, že já jsem v bezpečí.
A v ještě větším bezpečí budu, až konečně dopíšu ten článek.
Investigativně novinařila
Karolína „Karry“ Burešová
25-2-7 Zaléváme dokument (13 bodů)
 Upozornění: Přesný vzhled vysázených konstrukcí je v PDF verzi! Ve
webové verzi mohou být různé nepřesnosti, zvláště u vzhledu vysázených vzorců.
Pokud si tedy chcete být jisti tím, jak něco vypadá, sáhněte prosím po verzi
v PDF.
Upozornění: Přesný vzhled vysázených konstrukcí je v PDF verzi! Ve
webové verzi mohou být různé nepřesnosti, zvláště u vzhledu vysázených vzorců.
Pokud si tedy chcete být jisti tím, jak něco vypadá, sáhněte prosím po verzi
v PDF.
Seriál o TeXu pokračuje svým druhým dílem. Minule jsme se naučili
základy sazby, přeložili první dokumenty a vyzkoušeli matematický mód.
Tentokrát se ponoříme hlouběji do vnitřností TeXu, naučíme se psát makra a
zavřeme dokument do krabičky. Matematika přijde zkrátka, v této sérii se
neobjeví.
Připomínám, že preferovaný formát řešení je komentovaný zdrojový kód odevzdaný
jako prostý text. Nemusíte se snažit zdroják hezky vysázet apod., jen bychom
s tím měli zbytečně víc práce.
Sazba do boxů
TeX sází na stránku nepřeberné množství různých objektů. Aby se v tom
vyznal, každý z nich zabalí do krabičky, a dál už pracuje jenom s ní.
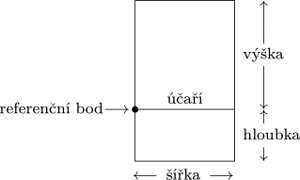
Všechno, co se sází, je tedy krabička – obdélníkový box, který má definovanou
výšku, šířku a hloubku.
TeX vidí jednotlivá písmenka jako boxy, z nich (a výplní mezi boxy) pak
staví řádky a celé stránky.
Tuto větu vidí přibližně takto:
Jednotlivé boxy se mohou skládat do horizontálních a vertikálních boxů – věty
v odstavci sestávají z písmen, která se naskládají do horizontálních boxů –
řádků. Řádky se pak nasypou do vertikálního boxu a z toho vznikne odstavec.
Do horizontálního boxu se tedy skládají objekty vedle sebe, kdežto do
vertikálního boxu pod sebe.
TeX řeší skládání do boxů automaticky, ale přesto je občas potřeba vyrábět
boxy explicitně. K tomu se můžou hodit následující primitiva (Primitivum je
základní řídící příkaz TeXu. Je vhodné jej nepředefinovat, protože by se pak
TeX mohl chovat podivně.):
\hbox{něco} a \vbox{něco} explicitně vyrobí horizontální nebo
vertikální box a do nich vloží příslušný obsah.
\hbox to 10cm{} je hbox široký přesně 10 cm. To znamená, že jeho
obsah se natáhne nebo smrskne přesně na zadanou velikost. Pokud to TeX
nezvládne, bude si stěžovat hláškou Overfull hbox nebo Underfull hbox.
Další možné jednotky délky jsou například
mm,
in,
pt,
případně
em a
ex. První čtyři jsou absolutní – jsou prostě dlouhé
centimetr, milimetr, palec nebo americký typografický bod (TeX point;
palce). Jednotky
em a
ex závisí na nastavené
velikosti písma. První z nich odpovídá šířce velkého písmene M, druhá z nich
odpovídá výšce malého písmene x.
Chcete-li hbox široký přesně stejně jako stránka (nezasahující do okrajů),
použijte \line{obsah} nebo \hbox to \hsize{obsah}. Obojí udělá
totéž. Rozměr \hsize určuje šířku, na kterou se sází odstavec.
\vbox to 10cm{} je vbox vysoký přesně 10 cm. Ještě existuje \vtop,
který má referenční bod v referenčním bodu prvního z objektů uvnitř, kdežto
\vbox má referenční bod v referenčním bodě posledního z objektů uvnitř.
Pozor, jakmile se uvnitř vboxu objeví odstavec, tak má vbox automaticky
šířku \hsize.
Proč tolik řeším referenční bod, respektive účaří? Protože v drtivé většině
případů se objekty skládají do horizontálního boxu tak, aby jejich účaří
lícovala s účařími toho horizontálního boxu.
A proč má vlastně každý box výšku a hloubku? Sázíme-li písmena na řádek, pak
některé znaky přesahují pod řádek: gjpqy – ty pak mají nenulovou hloubku.
Stejně jsou na tom například závorky: ()
Módy, čáry a prázdné místo
TeX operuje v různých módech. Na začátku je ve vertikálním módu, tedy skládá
boxy pod sebe. Jakmile začnete odstavec, přejde do horizontálního módu a skládá
boxy vedle sebe. Když skončí odstavec (\par), způsobí zalámání a přejde
zpět do vertikálního módu.
Taktéž uvnitř vboxu je ve vertikálním módu a uvnitř hboxu
v horizontálním, jen s tou výjimkou, že uvnitř boxů jste jistým způsobem
ohraničeni, například hbox se vám nezaláme.
Když chcete nakreslit vodorovnou nebo svislou čáru, použijte \hrule nebo
\vrule. Pozor, \hrule smí být použita jen ve vertikálním módu a
\vrule jen v horizontálním.
Vodorovná čára je standardně vysoká 0.4 pt a široká stejně jako box, který ji
ohraničuje (což je buď příslušný vbox, nebo celá stránka). Pokud se nám
to nelíbí, můžeme to změnit: \hrule width 2cm height 1pt depth 1pt.
Analogicky funguje svislá čára v horizontálním boxu.
Doporučuji za takovýhle příkaz napsat \relax, čímž zamezíte tomu, aby se
TeX pokoušel interpretovat nějaký následující text jako rozměry čáry.
Nakonec, když chcete bílé místo, použijte příkaz \vskip nebo
\hskip podle módu, ve kterém jste: \vskip 15mm
vytvoří 15 mm vertikální mezeru.
Pokud potřebujete roztažitelnou mezeru, použijte \vfil nebo
\hfil. Taková výplň se může roztahovat do nekonečna. Takže například
centrovaný řádek vypadá takto: \line{\hfil obsah\hfil}. Nebo
můžete použít konstrukci \centerline{obsah}, ta funguje stejně.
K boxům a výplním se ještě vrátíme ve čtvrté sérii a vysvětlíme si, jak fungují
doopravdy uvnitř různých procedur TeXu.
Makra
Máte-li pocit, že nějaký kus textu nebo kódu píšete vícekrát, jsou makra přesně
pro vás. Fungují podobně jako funkce v běžných programovacích jazycích.
Základní variantou je makro bez parametrů. Definuje se pomocí primitiva
\def:
\def\nazevmakra{obsah {\bf makra}}
Na takto definované makro se pak můžete kdekoli dál odvolat pomocí
\nazevmakra. Typické použití může být třeba takovéto:
\def\podpis{Karel Povolný, MFF UK\par}
Text dopisu 1
\podpis
\vfil\eject %% další stránka
Text dopisu 2
\podpis
\vfil\eject
\bye
Primitivum \par způsobí přechod na nový odstavec, stejně jako prázdný řádek.
S makry jste se už potkali v minulé sérii. Například \TeX je makro,
které vysází název programu TeX se správně posunutými písmeny.
Každé makro je definované jen v rámci své skupiny. Vyzkoušejte, jak se přeloží
například následující zdroják:
\def\makro{ABC}{\def\makro{DEF}\makro}\makro
Definicí již existujícího makra předefinujete stávající. Tím si můžete
absolutně rozbít prostředí, takže je potřeba si vybírat jména, která zatím
neexistují. Spolehlivý test vypadá například takto:
\def\isdefined#1{\ifx\undefined#1N\else Y\fi}
\isdefined{\macro}
\isdefined{\wtf} ...
Takové testování proveďte jednou. Ve chvíli, kdy makro definujete, si ověřte,
že tím nic nezkazíte. Pak takový test zrušte, nemá smysl, zbytečně by akorát
zaplevelil zdroják. Žádná budoucí verze plainu vám vaše makro
nerozbije (D. E. Knuth prohlásil, že plain nebude měnit, zůstane navěky stejný.).
Makra s parametry
Funkce obvykle můžou mít parametry, stejně na tom jsou makra.
\def\makro#1#2#3{Tohle je makro se třemi
parametry. Parametr 1 je #1, parametr 2 je #2
a parametr 3 je #3.}
\makro{kombajn}{bagr}{traktor}
Tohle je makro se třemi parametry. Parametr 1 je kombajn, parametr 2 je
bagr a parametr 3 je traktor.
Každé makro může mít až 9 parametrů, číslovaných od 1. Na n-tý parametr se
odkazujeme pomocí #n. Na každý parametr se můžeme odkázat klidně
vícekrát, nebo také vůbec.
\def\rekl#1{Karel řekl: \uv{#1}
Opravdu řekl: \uv{#1}}
\def\ignoruj#1#2#3{}
Makra s oddělenými parametry
Makra jsou mocnější zbraň, než by se mohlo zdát. Parametry totiž nemusí být
jenom uzavřené ve složených závorkách. Mohou být odděleny prakticky čímkoli.
Taková definice vypadá například takto:
\def\uloha#1: #2b{Úloha za #2 bodů: #1\par}
\uloha Třídění: 4b
\uloha Grafy: 5b
Parametr #1 v uvedeném příkladu tedy požere všechno až do dvojtečky a
následující mezery. A parametr #2 požere všechno od toho místa dál až do
nejbližšího b.
Mějme následující definici a zkoumejme chování makra \mc:
\def\mc#1::#2:#3::#4:{(#1)(#2)(#3)(#4)}
\it
\mc::::::
\mc:a::b:c::d:
\mc a::b::c::d::
\mc::::a::
\mc::a::::
::::::
Výstup vypadá takto:
()()()() (:a)(b)(c)(d) (a)(b)(:c)(d): ()()(:a)(():a)()(: )():::
Ještě stojí za poznámku, že je možno míchat oddělené a neoddělené parametry.
Platí, že za neodděleným parametrem není žádný oddělovač, v definici
\def\mc#1:#2#3#4:: jsou to parametry 2 a 3, kdežto 1 a 4 jsou oddělené
dvojtečkou, resp. čtyřtečkou.
Značka #n je zjednodušeně odkaz na příslušný parametr. Pokud byste
například ale chtěli napsat „makro, které definuje makro“, možná budete
potřebovat ##, což se expanduje na jediný znak #. Vyzkoušejte
následující kód:
\def\obalmakro#1#2{\def#1##1{##1#2##1}}

Úkol 1 [3b]
Nakreslete TeXem šachovnici 8×8. Hrana čtvercového
políčka nechť je přesně 2 cm. Bodujeme hlavně preciznost a čistotu kódu.
Měla by vypadat takhle, jen větší:
Úkol 2 [2b]
Definujte makro \uloha, které se bude volat takto:
\uloha 25-2-7: Zaléváme dokument (13)
a vysází se tak, aby výsledek
vypadal co nejvíce jako hlavička úlohy v letácích KSP. Skloňování u počtu bodů
můžete ignorovat, za výraz „3 bodů“ vám žádné body nestrhneme.
Kategorie znaků
TeX rozlišuje 16 kategorií znaků:
| Číslo | Název | Znaky |
| 0 | Escape char | \ |
| 1 | Open group | { |
| 2 | Close group | } |
| 3 | Math | $ |
| 4 | Alignment | & |
| 5 | End of line | CR (znak s ASCII kódem 13) |
| 6 | Parameter | # |
| 7 | Superscript | ^ |
| 8 | Subscript | _ |
| 9 | Ignored | znak s ASCII kódem 0 |
| 10 | Space | ␣ |
| 11 | Letter | a-z, A-Z |
| 12 | Other | cokoli jiného neuvedeného |
| 13 | Active | ~ |
| 14 | Comment | % |
| 15 | Invalid | znak s ASCII kódem 127 |
Znaky se mezi kategoriemi dají přehazovat užitím primitiva \catcode. Ve
skutečnosti je to 256 nezávislých 4-bitových čísel. Prostým uvedením ASCII kódu
znaku za \catcode vybíráte jeho kategorii: \catcode 71 odpovídá
kategorii znaku G, tedy 11.
Když chceme číslo vypsat (vysázet), použijeme primitivum \the:
\the\catcode 64 by mělo vysázet 12 (což je kategorie znaku @). Když
chceme číselnou hodnotu nastavit, použijeme následující konstrukci:
\catcode 64 = 13 %% Přehlednější varianta
\catcode 64 13 %% Totéž jako předchozí
Číslo je také možno zapsat jinak než decimálně: 'xyz je oktalový zápis,
"xy je hexadecimální zápis a `\x je ASCII kód znaku x.
Tedy '107, 71, "47 a `\G znamenají totéž číslo.
Kategorie znaků mají různý význam. Escape char uvozuje řídící sekvenci, avšak
nezapočítává se do ní: Je-li \catcode `\@=0, pak @par a
\par mají úplně stejný význam.
Open group a close group slouží k uzávorkování všeho možného. Stejně jako
u escape charu, nezáleží na ASCII kódu znaku, otevřít resp. uzavřít skupinu
může kterýkoli znak kategorie 1 resp. 2.
Uvozovací znak matematiky už znáte z minula. Alignment se používá v tabulkových
konstrukcích, to nás čeká v nějaké z dalších sérií.
Znaky end-of-line se chovají stejně jako mezera, až na to, že za EOL se
ignoruje zbytek řádky. Zkuste si to v praxi sami. Je-li navíc znak EOL na
začátku řádky, přeloží se na \par.
Parameter slouží k označení parametrů maker, také se s ním potkáme v tabulkách.
Subscript a superscript se používají v matematice na horní a dolní index.
Ignored a invalid se chovají téměř stejně – jsou ignorovány. V případě
invalidního znaku si ještě navíc TeX stěžuje.
U mezery se ignoruje ASCII kód a nahrazuje se bílým místem podle parametrů
fontu. Mezera je totiž divný znak – všimněte si, že jako jediná může mít
různou šířku podle potřeby.
Písmena a ostatní znaky se liší prakticky jedinou věcí – tím, jak se chovají
za escape charem. Řídící sekvence je totiž escape char + všechny následující
znaky kategorie 11, nebo escape char + jeden následující znak libovolné kategorie.
Aktivní znaky se chovají stejně jako řídící sekvence. Můžete je použít za
\def a definovat.
A konečně znak komentáře. Od toho se ignoruje vše až ke konci řádky.
Řádky
Možná vás zarazilo, že jenom znak CR (13) je end-of-line, když na Linuxu je
konec řádky znak LF (10).
TeX čte vstup po řádkách tak, jak je dostává od systému. Na Linuxu je to
tedy znak LF (kód 10), na Windows dvojice znaků CR+LF (13 a 10). Systémový znak
konce řádku se uřízne, ořežou se bílé znaky a na konec řádku se vloží znak CR.
Na vstupu může také probíhat netrivální překódování, obvykle se tím ale
není třeba zabývat.
Tokeny
Je důležité vědět, jak se TeX vlastně chová ke svému vstupu. Každý znak,
který se objeví, je tokenizován. Je určena jeho kategorie a jeho ASCII kód
společně s kategorií je uložen jako token. Tokeny budeme značit takto:
(znak, kategorie).
Dlužno podotknouti, že řídící sekvence se považuje za jeden token, tedy
například \par je jen jeden token (par, 0).
Tento kód nefunguje tak, jak byste čekali. Zkuste si to:
\catcode `\@ 11 %% @ je letter
\def\mac #1@{parametr: (#1)}
\catcode `\@ 12 %% @ je other
\mac něco @
\catcode `\@ 11 %% @ je letter
\mac něco @
Makro totiž očekává token (@, 11), nikoli (@, 12). A tak čte
tokeny jeden za druhým a čeká, jestli se neobjeví ten správný. A on se
neobjeví, protože i když postupně přečte \catcode `\@ 11 na pátém řádku,
tak jsou to pro něj stále jen tokeny, které přijdou do prvního parametru…
Expanze maker
Když se na nějakém místě objeví řídící sekvence, která je definována jako
makro, tak se TeX podívá, jak se má volat a jak mají vypadat parametry. Pak
čte tokeny jeden za druhým, dokud nenačte všechny parametry makra.
Přečtené tokeny odstraní a místo nich vloží definici makra. V ní nahradí
všechny výskyty #n příslušnými parametry a všechny dvojice tokenů
(#, 6) zredukuje na jednotlivé výskyty. A pak se na to pustí hledání
maker znova a znova, dokud tam nezůstanou jenom znaky a primitiva.
TeX navíc obsahuje omezení pro případ běžných překlepů (zapomenutých pravých
závorek) – standardně není povoleno, aby parametr makra obsahoval \par.
Když to potřebujete, předřaďte před definici makra \long:
\long\def\a#1{}
\def\b#1{}
\a{\par} %% projde
\b{\par} %% vyhodí chybu
Úkol 3 [8b]
Vymyslete, jak přepnout TeX do módu, kdy vysází na výstup (téměř) přesně to,
co má ve vstupu. Hodnotí se funkčnost, čistota kódu a nápad. Nebojte se zeptat
ve fóru, rádi poradíme a pomůžeme, také se tam můžete dozvědět různá doporučení
a upřesnění úlohy.
Spolu s hotovým makrem dodejte také ukázkové použití – vysázené řešení nějaké
jiné úlohy z této série se zdrojovým kódem. Toto řešení dodejte jako součást
řešení této úlohy, jinak nebude hodnoceno.
Pokud by vás náhodou napadlo prozkoumat zdrojové kódy LaTeXu, nedělejte to,
byť by se v nich jedno možné řešení dalo najít. Jsou spletité a akorát se
v nich zamotáte. Radši to zkuste vymyslet sami.
Během řešení úloh se vám ještě může hodit primitivum \let: Po provedení
\let\xyz\abc má \xyz identický význam jako \abc. Používá
se například na uložení původního významu řídící sekvence, případně na
„nakopírování“ makra. I když se pak změní význam původní sekvence
(v uvedeném příkladě \abc), význam nové sekvence zůstává. Vyzkoušejte:
\def\abc{ABC} \abc
\let\xyz\abc \xyz
\def\abc{DEF} \abc \xyz
Ve skutečnosti \let nepřiřazuje význam řídící sekvence, ale význam
tokenu, takže například můžete použít konstrukci \let\zavinac @ a pak
bude mít \zavinac stejný význam jako token (@, 12).
Také se vám při definování maker můžou hodit primitiva \begingroup a
\endgroup. Hodí se ve chvíli, kdy potřebujete například jedním makrem
otevřít a jiným pak zavřít skupinu, neboť definice makra musí být dobře uzávorkovaná.
Pozor, toto je jiný typ skupiny než ta, která je ohraničena tokeny (*, 1) a (*, 2) (U tokenů kategorie 1 a 2 nezáleží na kódu znaku, proto jsou uvedeny hvězdičky.).
Takže skupina otevřená primitivem \begingroup musí být uzavřená pomocí
\endgroup, jinak si TeX stěžuje (a obráceně skupina otevřená tokenem
kategorie 1 musí být uzavřená tokenem kategorie 2).
Toť protentokrát vše. Přeji mnoho štěstí při definování maker. Dotazy a
doplnění posílejte do fóra, stejně jako v první sérii.
Jan „Moskyto“ Matějka
Řešení
 Lehčí varianta (za 7 bodů): Řešte stejnou úlohu za předpokladu, že grafem
představujícím dopravní síť je cesta.
Lehčí varianta (za 7 bodů): Řešte stejnou úlohu za předpokladu, že grafem
představujícím dopravní síť je cesta.
 Základem organizovanosti je vybrání dobrého místa pro zastavení
dodávky. Mafiáni se kolem ní pak rozestaví v pomyslné čtvercové síti a
předávají si zboží, které se má dopravit na jednotlivá místa. Je
žádoucí, aby počet mafiánů potřebných na vyložení všeho zboží byl co
nejmenší. Pohyb mafiánů po čtvercové síti odpovídá pohybu krále po
šachovnici.
Základem organizovanosti je vybrání dobrého místa pro zastavení
dodávky. Mafiáni se kolem ní pak rozestaví v pomyslné čtvercové síti a
předávají si zboží, které se má dopravit na jednotlivá místa. Je
žádoucí, aby počet mafiánů potřebných na vyložení všeho zboží byl co
nejmenší. Pohyb mafiánů po čtvercové síti odpovídá pohybu krále po
šachovnici.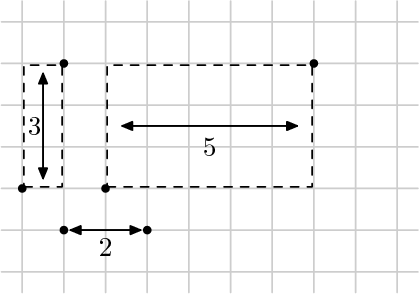
 Novinový článek se může nacházet v mnoha různých stavech a mezi každými dvěma
z nich ho může přesouvat nejvýše jeden redaktor. Každému takovému redaktorovi
se ale platí, a šéfredaktoři se rozhodli snížit výdaje. Chtějí tedy některé
redaktory propustit, aby součet platů těch zbylých byl co nejmenší.
Novinový článek se může nacházet v mnoha různých stavech a mezi každými dvěma
z nich ho může přesouvat nejvýše jeden redaktor. Každému takovému redaktorovi
se ale platí, a šéfredaktoři se rozhodli snížit výdaje. Chtějí tedy některé
redaktory propustit, aby součet platů těch zbylých byl co nejmenší.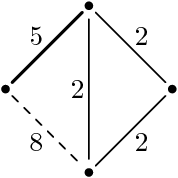
 Upozornění: Přesný vzhled vysázených konstrukcí je v PDF verzi! Ve
webové verzi mohou být různé nepřesnosti, zvláště u vzhledu vysázených vzorců.
Pokud si tedy chcete být jisti tím, jak něco vypadá, sáhněte prosím po verzi
v PDF.
Upozornění: Přesný vzhled vysázených konstrukcí je v PDF verzi! Ve
webové verzi mohou být různé nepřesnosti, zvláště u vzhledu vysázených vzorců.
Pokud si tedy chcete být jisti tím, jak něco vypadá, sáhněte prosím po verzi
v PDF.