Pátá série dvacátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 26-5-1: Made in China
- 26-5-2: Cesta pralesem
- 26-5-3: Náhradní kabel
- 26-5-4: Rozdělování jídla
- 26-5-5: Průjezd tunelem
- 26-5-6: Nejvyšší stavby
- 26-5-7: Partie piškvorek
- 26-5-8: Automatizovaný graf
26-5-1 Made in China (Zadání)
První úloha byla trochu netradiční tím, že správné řešení má časovou i paměťovou složitost konstantní. Číslo relé totiž dostaneme tak, že spočítáme bitový xor obou souřadnic (počítáme-li od nuly).
Pro jistotu si zopakujme, jak takový xor funguje: Obě čísla zapíšeme pod sebe ve dvojkové soustavě a kdekoliv se pod sebou objevily dvě různé číslice, píšeme do výsledku jedničku, všude jinde nulu. Takže třeba
11011 xor 10001 =
01010 = 10.
Zajímavější je, jak se na takovou věc přijde. Pokusíme se zde jeden z možných myšlenkových postupů nastínit.
Podívejme se na jednotlivé řádky trochu zvětšené tabulky ze zadání:
0 1 2 3 4 5 6 7
1 0 3 2 5 4 7 6
2 3 0 1 6 7 4 5
3 2 1 0 7 6 5 4
4 5 6 7 0 1 2 3
5 4 7 6 1 0 3 2
6 7 4 5 2 3 0 1
7 6 5 4 3 2 1 0
Nultý řádek odpovídá uspořádaným číslům. Na prvním jsou sousední čísla prohozená. Druhý prohazuje celé dvojice dohromady. Třetí kombinuje prohazováni prvního a druhého řádku. Čtvrtý vyměňuje celé čtveřice čísel. A tak dál.
Číslo řádku nám tedy přímo udává, jaký je vztah mezi číslem sloupce a samotným relé. Nejsnazší je se na číslo řádku podívat ve dvojkové soustavě. Každá jednička představuje jedno prohazování po blocích velikosti odpovídající příslušné mocnině dvojky. Například pátý řádek (ve dvojkové soustavě 101) prohazuje po blocích velikosti 4 a 1. Všechna čísla tedy budou posunuta nejdříve o 4 a následně o 1.
Chceme-li určit hodnotu na pozici [r, s], stačí zjistit, na jaké pozici je stejné číslo na nultém řádku. Z pořadí řádku již víme, o kolik budeme posouvat. Směr poznáme po celočíselném vydělení čísla s daným posunem. Lichá čísla posuneme doleva, sudá doprava.
Když se trochu zamyslíme nad uvedeným dělením, zjistíme, že se jen díváme na hodnotu jednoho bitu v čísle s. Protože posouváme o mocniny dvojky, tak tím vždy měníme hodnotu jenom jediného bitu. Každému bitu z čísla s změníme hodnotu právě tehdy, když je daný bit jedničkový i v čísle r. Dostali jsme tak přímo slibovaný bitový xor.
 Kdyby vám uvedený postup přišel nedostatečně formální a chtěli jste
důkladný důkaz, máte ho mít. Budeme postupovat indukcí a v i-tém
kroku indukce dokážeme, že tabulka velikosti 2i×2i popisuje
operaci xor.
Kdyby vám uvedený postup přišel nedostatečně formální a chtěli jste
důkladný důkaz, máte ho mít. Budeme postupovat indukcí a v i-tém
kroku indukce dokážeme, že tabulka velikosti 2i×2i popisuje
operaci xor.
Pro i=0, tedy tabulku 1×1, tvrzení evidentně platí.
Nyní krok od i k i+1. Tabulku 2i+1×2i+1 rozdělíme na čtyři podtabulky velikosti 2i×2i. Budeme jim říkat LH, PH, LD, PD (levá horní atd.).
LH nezávisí na ostatních podtabulkách, takže podle indukčního přepokladu odpovídá xoru. Navíc si všimneme, že v každém řádku i každém sloupečku této podtabulky leží všechna čísla od 0 do 2i-1. (Xorování čísel 0 až 2i-1 libovolnou konstantou z téhož rozsahu musí tato čísla jenom přeházet po dvojicích.)
Nyní se zaměřme na podtabulku PH. Shora není ničím ovlivněna, zleva jsou tabulkou LH blokovaná všechna čísla od 0 do 2i-1. Jsme tedy ve stejné situaci jako v LH, jenom je ke všem číslům přičteno 2i. Analogicky v tabulce LD.
Zbývá podtabulka PD. Ta má od LD i od PH zablokovaná čísla 2i až 2i+1-1, ale žádná nižší, takže opět dopadne stejně jako LH.
Toto chování podtabulek přitom přesně odpovídá xoru: LH a PD mají nejvyšší bit obou souřadnic stejný, takže vypadají stejně jako xor o bit kratších čísel; LD a PH ho mají různý, takže oproti xoru kratších čísel přibude ještě nejvyšší jedničkový bit, který odpovídá posunutí hodnot o 2i.
26-5-2 Cesta pralesem (Zadání)
Úvodem řešení si jdu sypat popel na hlavu, neboť jsem jako autorka úlohy zapomněla ohlídat, že se v zadání objeví některé předpoklady.
Předně, koeficienty přehlédnutelnosti jsou vždy nezáporné (ale většina z vás naštěstí předpokládala, že až tak podlí organizátoři nejsou).
Zadruhé, v zadání mělo být asi jasněji ukázáno, že navzdory běžnému vnímání pojmu cesta v této úloze připouštíme cesty, ve kterých se opakují vrcholy, dokonce i takové, ve kterých se opakují (neorientované) hrany.
Omlouvám se všem, kterým opomenuté předpoklady způsobily komplikace při řešení.
Ukažme si ještě, že ačkoli je neopakování hran a vrcholů obvykle velice přirozené, v naší úloze se zopakování skutečně může vyplatit. Představme si následující situaci (první číslo je přehlédnutelnost při průchodu rovně, druhé při odbočení):

Zatímco kdybychom odbočili rovnou, dostaneme přehlédnutelnost 9, při obejití políčka bude přehlédnutelnost pouze 4. To vysvětluje opakování vrcholů. A kdy se vyplatí zopakovat i hrany? Třeba v takovémto případě:
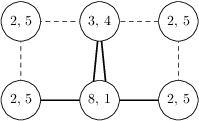
Přímý průchod má přehlédnutelnost 8, při „odskoku“ na jiné políčko dostaneme výslednou přehlédnutelnost 6.
Ale teď už honem na samotné řešení. Na hledání v grafech (a čtvercová mřížka je jen trochu speciální graf) se často vyplatí použít Dijkstrův algoritmus, který máme blíže popsaný v kuchařce o cestách. Jenže použití tohoto algoritmu brání fakt, že ohodnocení závisí na tom, z kterého vrcholu jsme přišli.
Potřebujeme tedy vstup nejprve nějak upravit. Každý vrchol si rozčtvrtíme, jednotlivé čtvrtiny budou reprezentovat právě to, odkud jsme do daného vrcholu přišli. Všechny čtvrtiny pak pospojujeme s příslušnými čtvrtinami sousedních vrcholů, hrany ohodnotíme podle toho, zda odbočujeme, nebo procházíme rovně.
Pozor na to, že v této fázi musíme u každé čtvrtiny vytvořit také hranu odpovídající situaci, kdy se na dané křižovatce otočíme čelem vzad. Ohodnocení této hrany bude odpovídat koeficientu přehlédnutelnosti při odbočení.
Ještě potřebujeme ošetřit počáteční a koncové políčko. Vytvoříme dva nové vrcholy. První z nich spojíme hranami ohodnocenými 0 se všemi čtvrtinami, do kterých se lze dostat z počátečního políčka, druhé spojíme se čtvrtinami políčka koncového.
V takto upraveném grafu (kde se na čtvrtiny díváme jako na plnohodnotné vrcholy) už jsou všechna ohodnocení jednoznačná, můžeme v něm tedy použít Dijkstrův algoritmus.
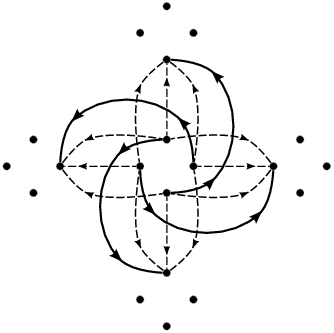
Na následujícím obrázku můžete sledovat, jak konstrukce grafu funguje. Nakreslili jsme hrany vedoucí ze čtvrtin jednoho vrcholu; plné hrany odpovídají chůzi rovně, čárkované zabočení.
Zbývá vyřešit složitost. Každý vrchol jsme nahradili čtyřmi, v novém grafu jich tedy máme konstanta-krát víc, podobně s hranami. Úpravu grafu bychom zvládli v lineárním čase, složitost Dijkstrova algoritmu je (při použití binární haldy) O((N+M) log N), kde N označuje počet vrcholů a M počet hran.
Ve čtvercové mřížce máme hran 4N (a v našem upraveném grafu 16N), celkovou složitost řešení tak můžeme odhadnout na O(N log N). Paměťová složitost je lineární, O(N).
26-5-3 Náhradní kabel (Zadání)
Přiznáváme, že úloha byla trochu složitější, než se mohlo podle deseti bodů zdát. Možná i proto dorazila pouze tři řešení. Trochu však mohla napovědět přiložená kuchařka o vyhledávání v textu.
Jak ale použít textové algoritmy k porovnávání stromů? Inu, budeme muset každý strom nějak popsat pomocí textového řetězce. Takovémuto popisu obvykle říkáme kód daného stromu. Různých kódování (tedy způsobů, jak stromům přiřazovat řetězce) můžeme vymyslet spousty. Na dvě z nich se teď podíváme.
Potřebujeme, aby v kódu bylo zachyceno pořadí synů. Toho můžeme dosáhnout tím,
že projdeme strom
do hloubky, v každém vrcholu vždy procházíme syny postupně od levého k pravému. Cestou si budeme
zaznamenávat každý vrchol, kterým projdeme, a to i když už se do něj poněkolikáté vracíme.
Pokud prohledávání zahájíme z jiného vrcholu,
dostaneme kód, který je rotací (Rotace znamená, že nějaký počet znaků přesuneme ze
začátku na konec. Jednou z rotací řetězce abcdef je například cdefab.) původního. To platí proto, že průchod je ekvivalentní „obejití
stromu po obvodu“:
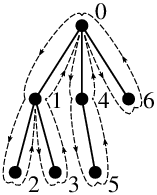
Řetězec reprezentující strom na obrázku by mohl vypadat následovně:
0 1 2 1 3 1 0 4 5 4 0 6.
Máme však problém. Co když nám někdo vrcholy přečísluje? V tu chvíli by se nám kódy porovnávaly dost špatně. Zkusme tedy vrcholy reprezentovat nějak jinak než jejich číslem. Můžeme použít například stupeň. To je číslo udávající počet hran, které z daného vrcholu vedou. Podívejme se opět na první strom:
3 3 1 3 1 3 3 2 1 2 3 1.
Musíme si ještě rozmyslet, že dva odlišné stromy nebudou mít nikdy stejný kód, jinými slovy, že z každého kódu dokážeme sestavit jednoznačně původní strom. To však naštěstí platí. Stačí si při vytváření stromu pamatovat, kolik hran jsme ve kterém vrcholu již použili, a tedy zda máme vytvářet nový vrchol, nebo se už vracíme. Zkuste si to nakreslit.
Pokud máme dva stromy se stejným počtem vrcholů, stačí nám každý z nich projít do hloubky a vygenerovat kód. Nyní jen ověříme, zda je jeden rotací druhého. To můžeme provést tak, že jeden kód napíšeme dvakrát za sebe a ve vzniklém řetězci se pokusíme najít ten druhý. Pokud hledání uspěje, představují oba stromy stejný kabel, jinak jsou různé. Pro samotné vyhledávání použijeme algoritmus KMP z kuchařky. Celé řešení tak pracuje v čase i prostoru O(N), tedy lineárně s počtem vrcholů.
Porovnání dvou kabelů pomocí KMP (C++)
Hledání dvojice kabelů
Teď umíme o dvou kabelech říct, zda jsou stejné. Co dělat, když máme více kabelů a cheme najít dvojici stejných? Mohli bychom použít algoritmus Aho-Corasickové k hledání kódů všech stromů najednou. Problém je v tom, že máme moc velkou abecedu – stupeň vrcholu může nabývat až N-1 různých hodnot (představte si třeba kabely ve tvaru „hvězdiček“ s různým počtem ramen). A Aho-Corasicková (alespoň ve verzi z kuchařky) potřebuje abecedu konstantně velkou.
Slibovali jsme na začátku, že ukážeme více způsobů kódování stromu do řetězce.
Teď je ta správná chvíle pro druhý z nich. Je vcelku jednoduchý. Strom projdeme
opět stejným způsobem, ale tentokrát si budeme zaznamenávat průchod po hranách.
Konkrétně při každém průchodu hranou zapíšeme, zda se pohybujeme dolů (D),
tedy přicházíme do nového vrcholu, nebo nahoru (N), čili se vracíme z již
prohledaného podstromu. Strom ze zadání tedy vytvoří kód
D D N D N N D D N N D N.
Kód nám přímo říká, jak máme strom kreslit. Nestane se nám proto, že by mu odpovídaly dva různé stromy. Je tu však jiný háček. Pokud začneme prohledávání z jiného vrcholu, dostaneme jiný kód.
Potřebovali bychom nějaký způsob volby počátečního vrcholu, který u stejných kabelů vybere stejný vrchol. Jednou z možností je najít takzvané centrum stromu. Získáme jej tak, že ze stromu postupně po krocích odebereme vždy všechny listy. Na konci nám zbude buď jeden jediný vrchol, nebo dva vrcholy spojené hranou. V prvním případě máme vyhráno. Ve druhém danou hranu rozdělíme – vytvoříme uprostřed nový umělý vrchol. Tento nový vrchol prohlásíme za centrum. Snadno si rozmyslíte, že shodné kabely (dokonce libovolné dva izomorfní stromy) opravdu mají stejné centrum.
Nejdříve si stromy rozdělíme do skupin podle počtu vrcholů. V každé skupině pak provedeme následující kroky:
- Najdeme centrum každého stromu.
- Každý strom projdeme do hloubky z jeho centra, a vytvoříme tak jeho kód.
- Sestrojíme vyhledávácí automat Aho-Corasickové pro jehelníček tvořený kódy všech stromů. U každé jehly si navíc musíme poznamenat (v koncovém vrcholu), ze kterého stromu vznikla.
- Pro každý ze stromů provedeme:
- Napíšeme jeho kód dvakrát za sebe, a takto vzniklý řetězec použijeme jako seno, na které spustíme výše vytvořený automat.
- Pokud automat najde výskyt nějaké jehly (kromě té, která odpovídá aktuálnímu stromu), znamená to, že aktuální kód je její rotací, tedy jsme našli dvojici stejných kabelů.
Všechny části stihneme opět v lineárním čase a zaberou jen lineárně prostoru, proto je i celý algortimus lineární s celkovým počtem vrcholů ve všech stromech dohromady.
26-5-4 Rozdělování jídla (Zadání)
Zadnání si můžeme přeformulovat také tak, že chceme vybrat nějakou množinu receptů tak, aby dohromady spotřebovaly surovin co nejvíc, ale zároveň nepřesáhly určitou mez (dostupné množství). To se náramně podobá problému batohu z kuchařky o dynamickém programování.
Přesněji pro (Připomeňme značení: K je počet surovin, N počet receptů, mi dostupné množství i-té suroviny a pro daný recept je ai množství i-té suroviny spotřebované tímto receptem, všechna čísla celá. ) K=1 jde přímo o problém batohu, jehož řešení je popsáno v kuchařce, pro vyšší K o jakousi „vícerozměrnou“ verzi.
Tu vyřešíme analogicky: pořídíme si K-rozměrné pole, kde na pozici (j1, …, jK) bude nenulová hodnota právě tehdy, když existuje podmnožina receptů, které dohromady spotřebují j1 první suroviny, j2 druhé, … Pole naplňujeme stejně jako u jednorozměrné verze: postupně procházíme předměty (recepty) a zkoušíme je všemi možnými způsoby do batohu přidat.
Alternativně se dá na recepty dívat jako vektory, které klasicky vektorově sčítáme a snažíme se je naskládat do batohu o kapacitě (m→). Naše vícerozměrné pole pak můžeme chápat jako pole indexované vektory.
Kuchařkové řešení
Při psaní tohoto řešení jsem nejdřív zkusil naprogramovat verzi přesně podle kuchařky (tedy opakované procházení celým polem odzadu a postupné zjišťování, jakých všech možných zaplnění batohu lze dosáhnout). Ve vícerozměrném poli „procházení odzadu“ odpovídá průchod do šířky z posledního („pravého dolního“) políčka. Později si ukážeme, jak takový průchod dělat efektivně.
Z důvodu šetření pamětí neukládáme do pole čísla receptů jako v kuchařce, nýbrž jen jedničky a nuly, podle toho, jestli extistuje tak velká množina receptů. Tím přijdeme o možnost zjistit, z jakých receptů se množina skládá, ale ježto nás zajímá jen celkové množství spotřebovaných surovin, nevadí to.
Leč takovéto řešení úspěšně vyřešilo jen jeden vstup (konkrétně osmý).
Problém je v tom, že kvůli průchodu do šířky čteme napřeskáčku z různých řádků vícerozměrného pole, a tedy z různých míst v paměti. A zatímco při teoretických úvahách pro zjednodušení předpokládáme, že všechny přístupy do pole trvají stejně (konstantně) dlouho, u opravdového počítače tomu tak není. Ukazuje se, že číst pole sekvenčně od začátku do konce (u vícerozměrného po řádcích) je výrazně rychlejší než neuspořádaně a napřeskáčku.
 Pokud se trochu zajímáte o fungování
počítačů, můžeme prozradit, že za to mohou přinejmenším dva jevy:
neefektivní využití keší procesoru (z každého načteného kešového
řádku obvykle použijeme jen jedno číslo) a prefetchování.
O obojím se můžete dozvědět např. v Medvědově textu
o programování s ohledem na hardware.
Pokud se trochu zajímáte o fungování
počítačů, můžeme prozradit, že za to mohou přinejmenším dva jevy:
neefektivní využití keší procesoru (z každého načteného kešového
řádku obvykle použijeme jen jedno číslo) a prefetchování.
O obojím se můžete dozvědět např. v Medvědově textu
o programování s ohledem na hardware.
Kuchařkové řešení „odpředu“
Proč vlastně procházíme pole odzadu? Představte si například, že máme jednorozměrnou verzi a jediný předmět o váze 2. Na začátku vypadá pole takto:
i 0 1 2 3 4 5
P[i] 1 0 0 0 0 0.
Pokud ho budeme procházet odzadu, dostaneme správný výsledek. Ale při průchodu odpředu získáme:
i 0 1 2 3 4 5
P[i] 1 0 1 0 1 0,
tedy stejný předmět jsme vložili do batohu několikrát. Tomu ale můžeme snadno zabránit tím, že si budeme do políček místo jedniček zapisovat číslo kroku, ve kterém byla vytvořena (stejně jako to dělá originální kuchařkové řešení, i když z jiných důvodů), a políčka vytvořená v aktuálním kroku ignorovat. Pak už můžeme s klidem zvolit průchod hezky po řádcích z levého horního rohu.
To ovšem zvýší paměťové nároky, neb si v poli musíme pamatovat hodnoty z rozsahu 0… N, tedy pro větší N nám nebude stačit jeden bajt na položku. A překvapilo mě, jak to bylo obtížné nepřekročit paměťové limity nastavené v CodExu. Nakonec jsem zjistil, že pro dodržení limitů se nedalo naprogramovat jedno univerzální řešení, ale muselo se rozlišit několik případů podle maximální hodnoty N, a pro každý zvolit jinak velký typ položek v matici (pro N ≤ 255 stačí jednobajtový, pro větší dvoubajtový). Ve zdrojáku je toto pro přehlednost jen zmíněno v komentáři.
Takovéto řešení už selhalo jen na třech vstupech (vypršel časový limit).
Problém obou algoritmů je také v tom, že receptů je málo, a tudíž hlavní pole je zaplněné velmi řídce (na drtivé většině míst má nuly). A náš algoritmus stráví spoustu času vytrvalým procházením tohoto moře nul, aby mezi nimi našel tu a tam nějakou nenulovou hodnotu.
Tomuto by velice pomohlo, kdybychom si pamatovali, kam nejdál jsme se v poli zatím dostali. Ale to jsem již ani nezkoušel testovat a programovat. Za chvíli si ukážeme ještě lepší řešení – ale nejdříve slibované odbočka o průchodu do šířky.
Průhod do šířky
Snadno si povšimneme, že při prohledávání dvourozměrné mřížky do šířky z jednoho jejího rohu projdeme v i-té fázi právě i-tou diagonálu v pořadí od tohoto rohu. Dobře je to vidět, když si do matice napíšeme vzdálenosti jednotlivých políček od pravého dolního rohu:
6 5 4 3
5 4 3 2
4 3 2 1
3 2 1 0
Takže vůbec nepotřebujeme frontu, ale průchod ve správném pořadí zajistíme vhodným dopočítáváním souřadnic na diagonálách (vizte zdroják).
Pro více rozměrů je dobrý mezikrok dívat se, jak by to dopadlo pro krychli. Tam se to dá představit tak, že postupně ukrajujeme z rohu.
Nyní bychom rádi tento postup zobecnili do více dimenzí. Podívejme se například na posloupnost souřadnic, které projdeme ve dvourozměrné tabulce výše:
0. vrstva: (4,4)
1. vrstva: (4,3) (3,4)
2. vrstva: (4,2) (3,3) (2,4)
...
Snadno si všimneme, že každou vrstvu tvoří políčka se stejným součtem souřadnic (ba dokonce všechna s takovým součtem), a tyto součty se postupně o jedničku snižují.
To není žádné velké překvapení. Každé políčko se do i-té vrstvy dostane tak, že je v nějaké souřadnici „levým sousedem“ některého políčka v (i-1)-ní vrstvě, tedy příslušnou souřadnici má o jedničku menší. A pokud má právě jednu souřadnici o jedničku menší, pak i součet souřadnic je pochopitelně o jedničku menší.
No a najít k-tice čísel s daným součtem už je snadné programátorské cvičení.
Řešení se spojákem
Problému řídkého pole se můžeme vyhnout tak, že si budeme udržovat spojový seznam nenulových políček. Pak stačí procházet tento seznam místo toho, abychom je v poli dlouho hledali.Mírnou nevýhodu může představovat, že spoják zabere nějakou paměť navíc. Ale vzhledem k tomu, že matice je zaplněná řídce, moc velký nebude. Navíc nyní nám opět stačí ukládat si do matice jen jedničky a nuly (Problému vícenásobného přidávání se můžeme vyhnout třeba tak, že budeme nová políčka připojovat na začátek spojáku. Nebo si je budeme skládat do pomocného spojáku, který k hlavnímu připojíme až na konci každého kroku.), pročež nám opět stačí jen jeden bajt na položku v hlavním poli (stačil by i jeden bit, ale tím nebudeme řešení zbytečně komplikovat).
Závěr
Doufám, že jste si z této úlohy odnesli to, že asymptotická složitost není vždy ekvivalentní s tím, jak rychle program poběží. A že více implementací ve stejném jazyce a se stejnou složitostí se může výrazně lišit dobou běhu.Pokud máte k něčemu z řešení (případně k implementaci) dotaz, nebojte se zeptat na fóru, rádi odpovíme.
Verze bez spojáku od konce (C)
Verze bez spojáku od začátku (C)
26-5-5 Průjezd tunelem (Zadání)
V řešení budeme značit W šířku a H výšku obdélníka.
Hodně z vás v mnohoúhelníku hledalo první a poslední místo, kde je mnohoúhelník vysoký alespoň H, a pak zkontrolovalo, jestli jsou tato dvě místa vzdálená alespoň W. Takové řešení však nefunguje. Nic nám nezaručuje, že obě nalezená místa se nachází ve stejné výšce. Dobrým protipříkladem je například kosodélník.
My si ukážeme dva možné přístupy k řešení. Jeden je založen na technice zametání roviny přímkou (anglicky plane sweeping či sweep line), kdy mnohoúhelník budeme zametat zároveň dvěma svislými přímkami vzdálenými W. Ve druhém řešení více využijeme vlastností konvexnosti a získáme všechna možná řešení pronikáním různě posunutých původních mnohoúhelníků. Obě řešení budou pracovat v čase O(n), kde n je počet bodů mnohoúhelníka.
První způsob řešení si pro jednoduchost popíšeme nejdříve jen pro hledání svislé úsečky dlouhé H. Na to nám bude stačit jedna zametací přímka.
Zametání přímkou je poměrně obecná technika pro řešení širokého spektra geometrických úloh. Spočívá v tom, že si představujeme přímku pohybující se spojitě napříč geometrickou scénu, která sleduje, co se děje „pod ní“ a umí „ohlásit“, když narazí na něco pro nás zajímavého.
V našem případě zametáme svislou přímkou, která se posouvá postupně přes mnohoúhelník od jeho nejlevějšího bodu po nejpravější. Pro každou polohu zametací přímky si (myšleně) spočítáme, jak vysoký je v daném místě mnohoúhelník. Pokud zametací přímka projde místem s výškou alespoň H, ohlásí na výstup příslušnou x-ovou souřadnici (stačí jednou).

Tohle je dobrý způsob, jak si řešení představit, ale určitě jej nemůžeme takto naprogramovat, neb bychom museli počítat výšku mnohoúhelníka pro každou z nekonečně mnoha x-ových pozic, kterými přímka prochází.
Všimneme si, že v každý okamžik (až na konečně mnoho výjimek) protíná zametací přímka právě dvě strany mnohoúhelníka. Navíc to, které dvě to jsou, se mění pouze, když přímka projde nějakým vrcholem mnohoúhelníka. Můžeme tedy podle x-ových souřadnic vrcholů rozdělit mnohoúhelník na svislé pásy, v každém z kterýchž protíná zametací přímka vždy nějakou pevnou dvojici stran mnohoúhelníka.
V rámci jednotlivého pásu už snadno určíme místo s výškou alespoň H, aniž bychom museli zkoušet všechny možnosti. K tomu se nám bude hodit malá odbočka do analytické geometrie.
Máme-li dané dva body A = [xA, yA], B = [xB, yB], pak všechny body na úsečce AB se dají vyjádřit soustavou rovnic:
| x | = xA + t(xB - xA) |
| y | = yA + t(yB - yA) |
| t | ∈<0, 1> |
Tedy po dosazení libovolného t z intervalu <0, 1> dostaneme souřadnice bodu ležícího na úsečce AB. Mějme nyní spodní úsečku AB a horní úsečku CD, chceme najít souřadnici x, kde jsou úsečky od sebe svisle vzdálené alespoň H. Tu získáme vyřešením následující soustavy (ne)rovnic:
| xA + t(xB - xA) | = xC + s(xD - XC) |
| yA + t(yB - yA) | ≤ yC + s(yD - yC) - H |
Neznámými jsou proměnné s a t. Pokud získáme řešení, kde s, t ∈<0, 1>, tak jsme našli místo, kam se nám vejde svislá úsečka délky H.
Implementace je nyní už jednoduchá. Obvod mnohoúhelníka si rozdělíme na horní a spodní polovinu – tedy části, které vedou od nejlevějšího bodu k nejpravějšímu „horem“, resp. „spodem“. Všimněte si, že pokud existuje víc nejlevějších (nejpravějších) bodů, je jedno, který si vybereme.
Nyní bychom chtěli postupně zleva doprava projít všechny pásy a pro každý z nich provést nás výpočet se správnou dvojicí úseček. To uděláme tak, že si budeme průběžně udržovat, která úsečka je aktuálně horní a spodní. Na začátku jsou to strany sousedící s nejlevějším vrcholem mnohoúhelníka. Poté postupně procházíme všechny zbylé body mnohoúhelníka v pořadí dle x-ové souřadnice a s každým vyměníme buď horní, nebo dolní úsečku za jinou, čímž přejdeme do sousedního pásu.
Jelikož úseček je celkem n a každou vyměníme maximálně jednou, tak celý algoritmus má časovou složitost O(n).
Nyní řešení upravíme pro hledání obdélníka. Na to nám jen jedna zametací přímka stačit nebude, ale budeme potřebovat dvě od sebe vzdálené W. Pro obě přímky si budeme udržovat horní a spodní úsečku, kterou zrovna prochází, a řešení budeme přepočítávat vždy, když některá z přímek projde vrcholem mnohoúhelníka.
A jak se bude lišit výpočet? Potřebujeme najít místo, kde vzdálenost výše postavené spodní úsečky a níže postavené horní úsečky je alespoň H. To spočítáme tak, že pravou horní a spodní úsečku posuneme o W doleva. Jednoduchými lineárními nerovnicemi zjistíme, pro jaké intervaly je která horní (resp. spodní) úsečka níže (resp. výše).
Tím se nám řešení rozpadne nejvýše na tři intervaly, protože v každé dvojici se maximálně jednou může změnit, která úsečka je horní (resp. spodní). Pak jen pro každý takový interval použijeme původní výpočet pro svislou úsečku o délce H. Časová složitost tohoto řešení je také O(n), protože pro obě zametací přímky uděláme maximálně n výměn úseček a mezi dvěma výměnami provádníme jen konstatně dlouhý výpočet.
Druhý způsob řešení zde pouze naznačíme. Každý konvexní útvar má tu vlastnost, že pokud v něm leží body A a B, tak pak v něm leží i celá úsečka AB. Speciálně pokud v mnohoúhelníku najdeme umístění všech rohů obdélníka, tak v něm leží i celý obdélník.
Opět se nejdříve podíváme, jak najít svislou úsečku délky H. Taková úsečka může mít svůj spodní konec ve všech bodech, které splňují, že bod o H nad nimi je také uvnitř mnohoúhelníka. Takže všechny takové body získáme tak, že mnohoúhelník posuneme o H nahoru a určíme jeho průnik s původním mnohoúhelníkem.
Průnik konvexních mnohoúhelníků je opět konvexní mnohoúhelník. Ten teď vezememe posuneme jej o W doleva a znovu nalezneme průnik. Tím dostaneme konečný mnohoúhelník, který obsahuje právě všechny body, kde obdélník může mít svůj levý horní roh.
Jak provedeme onen průnik mnohoúhelníků? Ukážeme si to pro první průnik. Ve druhém případě nám jen stačí situaci otočit o 90 stupňů a výpočet zopakovat. Jelikož jsou oba mnohoúhelníky shodné, tak nám jen stačí najít první a poslední průsečík horní části spodního mnohoúhelníka a spodní části horního mnohoúhelníka. Pak body mezi těmito průsečíky tvoří obvod výsledného průniku.
Na hledání příslušných průsečíků opět použijeme zametání přímkou a dostaneme řešení fungující v čase O(n).
26-5-6 Nejvyšší stavby (Zadání)
„Hledání maxim ve 2D nebo dokonce jen 1D oblastech matice? To jsou jasný haldy,“ řekne si kdekterý KSPák. Jenže v optimálním lineárním řešení se haldy nepoužívají, jen by ho zdržovaly. Pomocí hald či binárních výhledávacích stromů lze dosáhnout časové složitosti O(RS (log r + log s)), což ponecháme jako cvičení na práci s těmito strukturami. Lineární řešení však nevyžaduje kromě pár triků žádnou složitější datovou strukturu než spojový seznam.
Lehčí varianta fungovala jako nápověda, proto si pojďme nejprve vyřešit v lineárním čase 1D oblasti. Pro R = r = 1 máme tedy posloupnost S čísel a chceme zjistit nejvyšší číslo v každém souvislém úseku délky s. V prvním, nejlevějším úseku najdeme nejvyšší číslo snadno tím, že projdeme všechna čísla úseku. Poté budeme posouvat aktuální úsek o jedno číslo doprava.
Když posuneme úsek o jedna doprava, jedno číslo nám vypadne a jedno přibude. Pokud je nové číslo vyšší než dosavadní nejvyšší číslo úseku, bude i nejvyšším číslem nového úseku, jinak jím zůstane původní číslo. Problém nastane, když dosavadní nejvyšší číslo z posloupnosti vypadne. V tom případě by ho mělo nahradit druhé nejvyšší číslo, jež však také musíme udržovat. Kdyby však vypadlo i toto náhradní číslo, tak musíme mít ještě dalšího náhradníka, uvažte třeba klesající posloupnost.
Proto si budeme udržovat seznam kandidátů na nejvyšší číslo, reprezentovaný obousměrným spojovým seznamem. Prvním kandidátem bude samo nejvyšší číslo úseku, druhým bude nejvyšší číslo napravo od nejvyššího čísla úseku, třetím nejvyšší číslo napravo od druhého kandidáta, … Kandidáti budou tedy tvořit nerostoucí podposloupnost aktuálního úseku. U kandidátů si navíc budeme pamatovat jejich pozici v posloupnosti, abychom věděli, kdy vypadnou ze seznamu.
Při každém posunutí úseku o jedna doprava nám z kandidátů může vypadnout jen první, ten největší, a v tom případě se nejvyšší číslo úseku přesouvá na druhého kandidáta. Nové číslo, jež přibylo do úseku, přidáme do seznamu kandidátů. Navíc z tohoto seznamu od konce smažeme všechny kandidáty menší nebo rovné přidanému číslu, díky čemuž bude seznam kandidátů klesající podposloupnost úseku. Poslední číslo aktuálního úseku tak vždy bude kandidátem.
Jaká je časová složitost tohoto postupu? Nejlevější úsek a seznam kandidátů inicializujeme jistě v O(s), nicméně i posun úseku může zabrat až O(s), neboť kandidátů je až s a my je při jednom posunu můžeme všechny smazat. To se však stane jen relativně málo často.
K důkazu, že tento algoritmus je lineární, nám pomůže amortizovaná složitost. Každé číslo posloupnosti totiž do seznamu kandidátů jednou přidáme a maximálně jednou ho smažeme, čili celkový počet operací vyjde na O(S). Dodatečné paměti (bez vstupní posloupnosti) použijeme O(s), neboť kromě seznamu kandidátů a jejich pozic si už nepotřebujeme nic ukládat.
Nyní zobecníme řešení pro těžší, dvourozměrnou variantu. Výše představený postup pro jeden řádek budeme dělat najednou pro všechny řádky. Nejprve zpracujeme nejlevější úseky všech řádek a získáme sloupec maxim těchto úseků, na němž provedeme stejný postup jako na řádku, akorát s parametry R a r místo S a s. Tímto získáme maxima v obdélnících sousedících s levým okrajem, tedy první sloupec výsledné tabulky.
Pak posuneme úseky v každém řádku o jedna a opět dostaneme sloupec maxim, na kterém provedeme algoritmus pro jednorozměrnou variantu. Toto opakujeme, dokud nedojdeme s řádkovými úseky k pravému okraji. Algoritmus vrátí správné řešení, neboť maximum na obdélníku počítáme jako maximum z maxim na příslušných úsecích v jednotlivých řádcích.
Posouvání úseků na každém řádku zabere O(S), čili celkově O(RS). Jeden sloupec maxim z aktuálních úseků řádků zpracujeme v O(R), což dává opět O(RS), takže algoritmus je lineární s velikostí vstupu. Kromě vstupní matice čísel si stačí pamatovat kandidáty pro každý řádek a pro aktuálně zpracovávaný sloupec, tedy O(Rs+r) čísel.
Medvědí poznámka: Existuje ještě jiný, podobně elegantní způsob, jak vyřešit jednorozměrnou verzi. Posloupnost rozdělíme na bloky délky s a pro každý z nich předpočítáme prefixová minima (tedy minima od začátku bloku do každého jeho prvku) a podobně suffixová minima (od prvku do konce bloku). Pak si všimneme, že každý úsek délky s je buďto blok, nebo ho lze složit ze suffixu jednoho bloku a prefixu následujícího bloku. Stačí tedy v konstantním čase zkombinovat nejvýše dvě přepočítaná minima. Pokud bychom z tohoto algoritmu odvodili 2D řešení, bylo by stejně rychlé, ale potřebovalo by paměť na pomocnou matici.
26-5-7 Partie piškvorek (Zadání)
Řešení vybudujeme postupně: začneme absurdně zjednodušenou verzí úlohy a postupně se budeme všech omezení zbavovat. Hracímu plánu budeme říkat mřížka, křížkům a kolečkům symboly a souvislým úsekům stejných symbolů linie. Linii nejde ani jedním směrem rozšířit, z obou stran je tedy ohraničena mezerou, opačným symbolem, případně okrajem mřížky.
Jeden rozměr, jeden symbol, jedna operace
Prozkoumejme nejprve úlohu, v níž má mřížka jediný řádek o n políčkách, pokládáme jenom jeden druh symbolů (třeba křížky) a navíc je nikdy nemažeme.
Postačí udržovat si pro každé políčko mřížky, zda na něm nějaká linie začíná nebo končí, a pokud ano, tak kde leží její opačný konec.
Na počátku výpočtu žádné linie neexistují. Kdykoliv přidáme křížek, podíváme se, zda nějaká linie končí těsně před ním nebo začíná těsně za ním. Rozlišíme čtyři případy:
- Nenastane ani jedno: tehdy zakládáme novou linii o jednom křížku a k aktuálnímu políčku napíšeme, že na něm tato linie začíná i končí.
- Před námi končí linie, za námi žádná nezačíná: tehdy prodlužujeme linii před námi o jedno políčko. Posuneme koncovou značku a u té počáteční přepíšeme informaci o konci.
- Symetrický případ, kdy za námi linie začíná, ale před námi nekončí, ošetříme obdobně.
- Zbývá případ, kdy nastane obojí současně, čili naše políčko propojuje dvě linie. Tehdy zrušíme konec levé a začátek pravé, načež začátek levé necháme ukazovat na konec pravé a naopak.
Navíc se pokaždé podíváme, zda nově vzniklá linie není delší než dosavadní maximum. To vše zvládneme v konstantním čase, navíc ale musíme připočíst lineární čas na inicializaci pole začátků a konců.
Přidáváme mazání
Nyní strukturu vylepšíme, aby uměla křížky mazat. Opět mohou nastat čtyři případy: buďto byl smazaný křížek osamocený (tehdy prostě zrušíme celou linii), nebo leží na začátku či na konci linie (to poznáme podle značek začátků a konců a linii prostě zkrátíme), nebo leží uvnitř linie. Tehdy potřebujeme najít její začátek a konec a linii rozdělit na dvě.
První tři případy rozpoznáme pomocí značek na aktuálním poličku a jeho sousedech. Pokud ale políčko leží kdesi uvnitř dlouhé linie, potřebujeme rychle zjistit, kde leží nejbližší značka.
Pořídíme si tedy navíc vyhledávací strom, v němž si budeme pamatovat pozice všech značek začátku. Kdykoliv mažeme nějaký křížek, zeptáme se stromu, jaká je nejbližší nižší pozice začátku. To strom zvládne v logaritmickém čase a jakmile známe polohu začátku, příslušná značka nám prozradí, kde leží konec. Navíc musíme strom aktualizovat, kdykoliv se nějaký interval změní. To naštěstí nastane O(1)-krát za operaci, takže to celkově trvá O(log n).
Ještě se nám ovšem zkomplikovalo udržování nejdelší linie. Už totiž není pravda, že by se nejdelší linie stále jen prodlužovala. Pořídíme si proto další vyhledávací strom, do kterého budeme ukládat délky všech existujících linií. Jelikož se délky linií mohou opakovat, budeme si u každé délky pamatovat počítadlo, abychom věděli, kdy ji smazat. Každá operace s intervaly opět způsobí O(1) změn stromu, které potrvají O(log n). Na konci operace se pak stačí zeptat tohoto stromu (budeme mu říkat souhrnný strom) na aktuální maximum.
Souhrnný strom bychom navíc mohli snadno upravit, aby si pamatoval nejen délky linií, ale i jejich polohy. Pak bychom věděli nejen jak dlouhá je maximální linie, ale také kde přesně leží.
Jedno umístění nebo mazání křížku nám tedy trvá O(log n) a navíc potřebujeme čas O(n) na inicializaci struktury.
Jednorozměrná verze s křížky a kolečky
Teď je na čase si přiznat, že v piškvorkách hrají nejen křížky, ale také kolečka. To nám úlohu zkomplikuje jen kosmeticky: pořídíme si dvě datové struktury, jedna si bude pamatovat linie křížků, druhá linie koleček. A necháme je pracovat se společným souhrnným stromem, takže rovnou dostaneme maximum z křížků a koleček. Časová složitost se asymptoticky nezměnila.
Dvojrozměrná verze
Opravdová piškvorkovnice je ovšem dvojrozměrná, řekněme n×n. Poradíme si jednoduše: pořídíme si samostatnou jednorozměrnou strukturu pro každý řádek, každý sloupeček i každou úhlopříčku a kdykoliv umístíme nebo smažeme symbol, řekneme o tom všem čtyřem strukturám, ve kterých dané políčko leží. Opět všechny struktury necháme pracovat se společným souhrnným stromem, takže nám budou udržovat globální maximum.
Časová složitost na operaci zůstává O(log n), protože pokaždé přepočítáváme O(1) struktur, z nichž každá pracuje v logaritmickém čase. Na začátku výpočtu inicializujeme řádově n struktur o n prvcích, což dohromady trvá O(n2).
Malé kouzlo na závěr
 Celé řešení je ještě možné zrychlit. Stačí si všimnout, že do vyhledávacích
stromů ukládáme pouze čísla od 1 do n. Můžeme proto místo klasických stromů
použít některou ze speciálních celočíselných datových struktur, například
van Emde-Boasovy stromy. Jejich popis najdete ve skriptíčkách
Krajinou grafových algoritmů. Zde
prozradíme pouze to, že pro hodnoty od 1 do U jim jedna operace trvá
O(log log U), takže se naše piškvorková struktura zrychlí na O(log log n)
na operaci plus O(n2) na inicializaci.
Celé řešení je ještě možné zrychlit. Stačí si všimnout, že do vyhledávacích
stromů ukládáme pouze čísla od 1 do n. Můžeme proto místo klasických stromů
použít některou ze speciálních celočíselných datových struktur, například
van Emde-Boasovy stromy. Jejich popis najdete ve skriptíčkách
Krajinou grafových algoritmů. Zde
prozradíme pouze to, že pro hodnoty od 1 do U jim jedna operace trvá
O(log log U), takže se naše piškvorková struktura zrychlí na O(log log n)
na operaci plus O(n2) na inicializaci.
26-5-8 Automatizovaný graf (Zadání)
Část z vás se automatů ve vrcholech grafu zalekla a nepouštěla se dále než za první nebo druhý úkol. Ale jsem velmi rád, že se mezi vámi našlo i dost odvážlivců, kteří se rozhodli poprat se i se zbylými úkoly.
Úkol 1
Tento úkol byl velmi podobný druhému ukázkovému příkladu – vyslat dva signály proti sobě a tam, kde se potkají, označit vrchol. Abychom ale označili vrchol ve třetině kružnice, musel by jeden ze signálů běžet dvakrát tak rychle než druhý.
Zrychlit signál neumíme (musel by přeskakovat najednou přes dvě hrany, což ale nejde, protože každý automat ve vrcholu vidí pouze do svých bezprostředních sousedů), ale umíme jeden ze signálů zpomalit na polovinu a tím zařídit stejný efekt. Zpomalení na polovinu uděláme tak, že signál v každém vrcholu na jeden takt pozdržíme a teprva poté pošleme dál.
Abychom označili vrcholy ve třetině a dvou třetinách, budeme muset na začátku vyslat čtyři signály. Na jednu stranu signál A o normální rychlosti a signál B o poloviční rychlosti, na druhou stranu naopak (A o poloviční a B o normální). A poté, v místě kde se potkají signály A a B, tam označíme výsledné vrcholy a počkáme na ustálení.
Signály nám tak obejdou kružnici jen jednou a celkově tak vykonáme O(N) taktů výpočtu. Program by mohl vypadat třeba takto:
# Proměnné:
# x - rozsah 0..1
# signalA, signalB - rozsah 0..1, vých. hod. 0
# statusA, statusB - rozsah 0..2, vých. hod. 0
if x == 1:
# Vyšleme úvodní signál na obě
# strany a skončíme
signalA = signalB = 1
stop
# Dostali jsme signál z obou stran
if S[0].signalA and S[1].signalA:
x = 1
stop
# A proti směru: Počkáme na odeslání 1 tah
elif S[0].signalA and statusA == 0:
statusA = 1
# A po směru nebo již čekáme: Odešleme ihned
elif S[1].signalA or waitA:
statusA = 2 # Abychom neodesílali znovu
signalA = 1
# ... obdobně pro signalB a statusB
Úkol 2
K nalezení kostry grafu použijeme simulaci prohledávání do šířky. Spustíme prohledávání z jednoho vrcholu a budeme postupně přivěšovat vrcholy, které patří do dosud nenavštívené části grafu. Každý vrchol přivěsíme za právě jednu hranu, tedy nám určitě nikdy nevznikne cyklus a výsledný graf po zastavení bude strom.
Pokud byl původní graf souvislý, tak ke každému vrcholu existuje od počátečního vrcholu cesta. Ve chvíli, kdy zpracujeme sousední vrcholy, navěsíme i tento vrchol do vznkajícího stromu. Protože výsledný strom bude obsahovat všechny vrcholy, vznikne nám tak kostra.
Prohledávání budeme dělat tak, že každý dosud nezpracovaný vrchol bude sledovat své sousedy. Ve chvíli, kdy se nějací sousedé stanou součástí vznikajícího stromu (stanou se zpracovanými), vybere si z nich aktuální vrchol jednoho a s tím se spojí hranou (nastaví odpovídající proměnnou na svojí straně na jedničku).
Končit budeme ustálením.
# Proměnné:
# a - vstup, rozsah 0..1
# kostra[i] - výstup, rozsah 0..1, výchozí 0
# Už jsem v kostře, jen sleduji sousedy.
if a == 1:
for i in range(5):
if S[i].kostra[P[i]]:
kostra[i] = 1
# Nejsem v kostře. Pokud je nějaký soused
# v kostře, připojím se k němu.
else:
for i in range(5):
if S[i].a:
kostra[i] = 1
a = 1
Prohledání grafu do šířky trvá asymptoticky lineárně dlouho a tedy i celý program pro grafomat skončí po ustálení za O(N) kroků (tím, že je graf 5-regulární, by šel odhad ještě upřesnit, ale zlepšíme ho tak pouze o konstantu).
Úkol 3
V zadání nám uteklo, že graf je souvislý, za což se omlouváme. Nikoho z řešitelů to však nezmátlo a všichni správně řešili verzi pro souvislý graf.
| 1 |
| N |
Budeme potřebovat vymyslet řešení, které za každý vrchol stráví nějaký konstantní čas, než předá práci dalšímu vrcholu. K tomu se přímo nabízí využít DFS neboli prohledávání do hloubky.
Začneme v označeném startovním vrcholu a půjdeme po dosud nenavštívených vrcholech tak dlouho, dokud to půjde. Ve chvíli, kdy narazíme na slepou uličku, tak se vrátíme a zkusíme to jinudy. Po každé hraně vzniklého DFS stromu tak právě jednou sestoupíme dolů a právě jednou se po ní vrátíme, skončíme opět ve startovním vrcholu.
Můžeme si to představit tak, že vrcholy si budou předávat nějaký token. Vrchol, který drží token, si vždy vybere nějakého ze sousedů, kterému token odešle (nastaví u sebe proměnnou, které si pak soused v dalším taktu všimne) a správný soused si token převezme. Při vracení se zpět budeme navíc vrcholy zastavovat a výpočet grafomatu tak ukončíme celkovým zastavením.
Tím, že obejdeme graf pomocí DFS, nám vznikne strom na N vrcholech. Ten má ale N-1 hran, takže celkově výše popsaný postup provede 2N-2 kroků. Tím, že na začátku počkáme právě dva kroky, už dosáhneme přesného počtu 2N kroků. Program může vypadat třeba takto:
# Proměnné:
# start - vstup, rozsah 0..2
# navstiveno - rozsah 0..1, výchozí 0
# uzavreno - rozsah 0..1, výchozí 0
# smer - rozsah 0..K, výchozí K
# Hlavní funkce: Pokusí se mezi sousedy najít
# zatím nenavštíveného a předat mu token, pokud
# ale takového nenajde, uzavře aktuální vrchol.
def predejToken():
for i in range(K):
if S[i].navstiveno == 0:
# Pošleme token tímto směrem
smer = i
return
# Pokud se nám nepovede token nikam
# poslat, uzavřeme tento vrchol
uzavreno = 1
stop
# 1. Na startu musíme počkat
if start == 1:
start = 2
elif start == 2:
start = 0
predejToken()
# 2. Sledujeme, jestli nam nekdo neco neposlal
elif navstiveno == 0:
for i in range(K):
# Jestli ukazuje na nás
if S[i].smer == P[i]:
navstiveno = 1
predejToken()
# 3. Pokud už jsme někam token poslali,
# sledujeme, jestli se nám nevrací
else:
if S[smer].uzavreno:
predejToken()
Úkol 4
Kdybychom měli k dispozici počítadlo, byl by úkol velmi jednoduchý. Stačilo by jen si závorky postupně posouvat doleva k prvnímu vrcholu, zde je zpracovávat a počítat počet otevřených závorek. Pokud bychom se někdy dostali pod nulu, skončili bychom s chybou, stejně jako kdyby na konci mělo počítadlo nenulovou hodnotu.
Všechnu práci budeme dělat v prvním, označeném, vrcholu. V ostatních budeme jen posouvat závorky. Vrchol, který bude potřebovat závorku, si ji vždy nakopíruje od souseda a zapíše v nějaké domluvené proměnné, že si ji vzal. Druhý vrchol se podívá na tuto proměnnou svého souseda, zjistí, že byl „okraden“, a sebere závorku sousedovi na druhé straně.
Takto lze zařídit postupné posunutí všech závorek až do prvního vrcholu, kde se zpracovávají. Jenom musíme na přesun počítat se dvěma kroky výpočtu: v prvním seberu závorku sousedovi, ve druhém teprve soused zjistí, že mu chybí, a sebere ji zase svému sousedovi. Zbývá zařídit počítadlo.
Počítadlo si ale jednoduše můžeme vyrobit jako bitové počítadlo kombinací vícero vrcholů – nejblíže prvnímu vrcholu budu mít nejnižší bity a dále bude jejich hodnota vzrůstat. Největší číslo, které budeme potřebovat, bude N – to zakódujeme do log N bitů a vrcholy nám tak bohatě stačí.
Na začátku výpočtu bude počítadlo ve všech vrcholech nastaveno na nulu. Při přičtení jedničky zvětšíme počítadlo v aktuálním vrcholu o jedna a kdyby mělo přetéct, nastavíme ho na nulu a do domluvené proměnné uložíme přenos. Soused se podívá na naší domluvenou proměnnou a případně přenos přičte ke své hodnotě.
Odčítání bude fungovat obdobně: Pokud budu mít ve svém vrcholu jedničku, změním ji na nulu a končím, pokud ale budu mít nulu, změním ji na jedničku a směrem dál odešlu přenos s hodnotou mínus jedna. Pokud takový přenos dojde nazpět až k prvnímu vrcholu, dostal jsem se právě do záporných čísel a vyhlásím chybu.
Poslední, co zbývá, je po konci výpočtu zkontrolovat, že nám v počítadlu zbyly samé nuly. To uděláme jednoduše tak, že vyšleme z prvního vrcholu signál, který když cestou narazí na jedničku, vyhlásí chybu. Pokud dojde nazpět až k prvnímu vrcholu, je uzávorkování správné a zahlásíme úspěch.
# Proměnné:
# prvni -vstup, rozsah 0..1
# zavorka - vstup, rozsah -1..1
# prenos_zavorky - rozsah 0..1, výchozí 0
# pocitadlo - rozsah 0..1, výchozí 0
# prenos - rozsah -1..1, výchozí 0
# vystup - rozsah 0..1, výchozí 1
# signal - rozsah 0..1, výchozí 0
levy = S[0]
pravy = S[1]
# Reset hodnot
prenos = 0
signal = 0
if prvni == 1:
# 1. Počítadlo přeteklo do mínusu, nebo přišel
# signál s chybou -> chyba
if levy.prenos == -1 or levy.vystup == 0:
vystup = 0
stop
# 2. Zpracování závorek, dokud jsou
if prenos_zavorky:
# Jenom počkáme, než soused bude mít
# připravenou novou závorku
prenos_zavorky = 0
else:
if zavorka == 1:
prenos = pocitadlo
pocitadlo = (pocitadlo + 1) % 2
elif zavorka == -1:
prenos = -1 * pocitadlo;
pocitadlo = (pocitadlo - 1) % 2
# 3. Závorky došly, spuštění kontroly
else:
signal = 1
# Zkopírujeme si závorku zprava
zavorka = pravy.zavorka
prenos_zavorky = 1
else:
# Reset hodnot
prenos_zavorky = 0
# 1. Pokud přišla chyba, vyhlásíme ji také
# a končíme
if levy.vystup == 0 or pravy.vystup == 0:
vystup = 0
stop
# 2. Přenos závorek
if levy.prenos_zavorky:
# Pokud ještě existuje závorka napravo
if pravy.prvni != 1 and pravy.zavorka != 0:
zavorka = pravy.zavorka
prenos_zavorky = 1
else: # Již není závorka napravo
zavotka = 0
# 3. Počítadlo
if levy.prenos == 1:
prenos = pocitadlo
pocitadlo = (pocitadlo + 1) % 2
if levy.prenos == -1:
prenos = -1 * pocitadlo;
pocitadlo = (pocitadlo - 1) % 2
# 4. Závěrečná kontrola počítadla
if levy.signal:
if pocitadlo =! 0:
vystup = 0
stop
else:
signal = 1
Přesunování závorek nám na každou z nich zabere 2 kroky, aktualizaci počítadla zvládneme dělat průběžně během posouvání závorek, a nakonec ještě jednou projdeme všechny vrcholy. Dohromady tak provedeme O(N) kroků výpočtu.