Čtvrtá série dvacátého šestého ročníku KSP
Celý leták v PDF.
I v této sérii můžete získat sladkou odměnu! Každému, kdo
v této sérii získá alespoň dva body z každé úlohy, pošleme čokoládu.
Zadání úloh
Jacob pomalu popadal dech. Právě se mu podařilo uniknout před proudem lávy
valící se z rozběsněné sopky. Dokonce našel malý převis, který ho uchránil
před deštěm kamení a žhavého sopečného popela.
Jeho myšlenkami letěly vzpomínky na události, které zažil od okamžiku,
kdy ho ztroskotání vesmírné lodi UFC Freya uvěznilo na této planetě.
První opatrné zkoumání pralesa. Setkání s mimozemšťany. Polámané nohy.
Dlouhé léčení. Tajuplná Ada. Podzemní bratrstvo. Darovaný meč. Probuzený
vulkán …
Podařilo se aspoň části členů Bratrstva utéci do bezpečí, nebo všechny
v jejich podzemním komplexu zaplavila láva? To se Jacob ještě nějaký
čas nedozví – teď mu totiž nezbývá než vyčkat v úkrytu, dokud se sopka
neuklidní. Aby zahnal nervozitu, zkouší hrát nejrůznější hry pro jednoho
hráče neboli solitéry. Třeba s kamínky, těch je teď všude plno.
26-4-1 Kamínkový solitér (10 bodů)
Jacob hraje následující hru. Nejprve vytvoří n hromádek kamínků.
Pak odebírá kamínky podle následujícího pravidla: Vždy si vybere dvojici
různě velkých hromádek a z té větší odebere tolik kamínků, kolik jich je na té
menší. Cílem hry je zbavit se co nejvíce kamínků.
Vymyslete algoritmus, který pro tuto hru najde optimální strategii.
Na vstupu dostane počet hromádek n a počáteční počty kamínků h1,… ,hn.
Výstupem má být posloupnost tahů typu „od hi odečti hj“ taková,
že po provedení těchto tahů bude součet h1+… +hn nejmenší možný.
 Lehčí varianta (za 4 body):
Rozmyslete si, jak úloha dopadne pro dvě hromádky. Své tvrzení dokažte.
Lehčí varianta (za 4 body):
Rozmyslete si, jak úloha dopadne pro dvě hromádky. Své tvrzení dokažte.
Řešení
Jacob se s trhnutím probudil. Co to bylo? Venku byla tma jako v pytli,
hvězdy pohltil všudypřítomný sopečný prach. Opodál cosi šramotilo. „Psst, Jacobe,
to jsi ty?“ špitl hlas nápadně podobný Adinu. Po chvilce oboustranného
ujišťování se ze tmy vynořila Ada spolu s dalšími čtyřmi mimozemšťany,
kteří s Jacobem zkoumali kráter sopky. Bylo to včera, ale zdálo se to jako
věčnost …
Přeci jen se jim podařilo uniknout potokům prskající lávy a schovat se
ve stejných skalách, které poskytly azyl Jacobovi. Jacob si pomyslel,
že jsou jistě celí žhaví zjistit, co se událo v okolí. Nejspíš i doslova.
Každopádně jim nezbývá než zůstat v úkrytu, dokud se popel nerozptýlí. Zatím
není vidět na krok a kdo ví, jak se erupcí změnila krajina.
Sedli si tedy společně na teplou zemi. Ze začátku tiše, ale po chvíli
jeden z tvorů vytáhl jakési zvíře podobné bažantovi, které našel pod
vrstvou rozpáleného popela. Zjevně dobře upečené. Po dobrém jídle
nervozita opadla a Jacob využil příležitosti a zeptal se na pár věcí,
které mu už delší dobu vrtaly hlavou.
Například proč mají všichni členové Bratrstva na krku podivný amulet –
náhrdelník s řadou barevných korálků. Každý s jinou kombinací barev,
ale přeci jen bylo možné vysledovat určité podobnosti. Ada usoudila,
že teď už před Jacobem není potřeba nic tajit. Prozradila mu,
že amulet slouží jako poznávací znamení členů Bratrstva
a obsahuje heslo, které se čas od času mění.
26-4-2 Výroba amuletu (10 bodů)
Amulet definujeme jako posloupnost červených, zelených
a modrých korálků. Heslo je také nějaká posloupnost korálků.
Amulet obsahuje heslo, pokud lze z amuletu vypustit některé
korálky tak, aby zbylo právě heslo. Matematik by tedy řekl,
že heslo tvoří vybranou podposloupnost amuletu.
Ada zná nové heslo a chce svůj amulet upravit tak, aby
toto heslo obsahoval. Upravovat ho může vkládáním korálků
na libovolné místo. Ovšem výroba jednoho korálku trvá nějaký
čas závislý na jeho barvě, tak by chtěla vymyslet, kam vložit
který korálek, aby tím celkově strávila co nejméně času.
Vymyslete algoritmus, který jí v tom pomůže. Na vstupu dostane
dva řetězce písmen R, G a B: amulet a heslo.
Mimo to ještě dostane celá kladná čísla cR, cG a cB
udávající, kolik času trvá vyrobit korálek které barvy.
Výstupem algoritmu má být posloupnost operací „za i-tý korálek
vlož korálek barvy b“, která zabere nejkratší možný čas.
Řešení
Noc pokračuje. Skupinka se snaží usnout, ale ve stísněném
prostoru pod převisem to jde jen obtížně. Polštáře tu nejsou,
tak musel Jacob vzít zavděk jakýmsi kamenem. Nepříjemně
tlačil do ucha a navíc se z něj ozývalo podivné zvonění,
jako by v hlubinách planety nějaký skřítek mlátil kladivem
do skály.
Zvonění je ale podivně pravidelné. Skoro jako by si ti skřítci
posílali nějaké zprávy. Jacob místo počítání oveček přemýšlí, jak by
takový přenos zpráv mohl fungovat. Snaží se vymýšlet různé způsoby
a zkoušet pomocí nich zvonění dešifrovat. Evidentně to k ničemu
nebude, ale aspoň svou mysl unaví a konečně usne.
„J…S…M…E…Z…A…S…Y…P…“
Cože??!!! Jacob ihned vzbudil ostatní a společně naslouchali
skalám. Text byl poněkud zmatený, postupně však pochopili, že se
jedná o víc překrývajících se zpráv. Posílají je skupinky členů
Bratrstva uvězněné na různých místech v podzemí.
Do jeskynního systému nejspíš nenatekla žádná láva, ale výbuch
na mnoha místech zavalil chodby. Ada hned začala do vrstvy
popela zapisovat, které části podzemí zůstaly propojené,
ale situaci znepřehledňovalo, že se zprávy o spojení jeskyní
často opakovaly.
26-4-3 Obnovené spojení (10 bodů)
Mějme n jeskyní a m neuspořádaných dvojic {xi,yi},
které popisují, že jeskyně xi je propojena s jeskyní yi.
Navrhněte co nejefektivnější algoritmus, který z tohoto seznamu
odstraní opakující se dvojice.
Výstupem je tedy seznam navzájem různých dvojic, které se alespoň
jednou vyskytly ve vstupním seznamu. Na pořadí dvojic nezáleží.
Řešení
Ada dokreslila plán podzemí a ve tváři jí zazářila radost. Právě zjistila,
že navzdory všem závalům stále existuje cesta, jak se do všech obydlených
jeskyní dostat. Značně složitá, ale je tu.
Vzduch, který se mezitím trochu pročistil, ovšem odhalil, že okolní
skaliska jsou zasypaná hromadami sopečného popela, tufu a kamení.
Dříve důvěrně známé kopce se najednou proměnily v nepřehlednou
krajinu plnou skrytých nebezpečí.
Skupina se rozdělila a každý dostal za úkol důkladně, ale velmi
opatrně prozkoumat část okolí a pokusit se nakreslit mapu. Když se
vrátili, zjistili, že mapy se poněkud překrývají. Některá místa
nejsou zmapována vůbec, zatímco jiná velmi důkladně. Jak se
v tom vyznat?
26-4-4 Skládání mapy (12 bodů)
 V rovině je položeno několik kusů mapy. Kusy mají tvar obdélníků
se stranami rovnoběžnými s osami souřadnic.
V rovině je položeno několik kusů mapy. Kusy mají tvar obdélníků
se stranami rovnoběžnými s osami souřadnic.
Naším úkolem je vytvořit datovou strukturu, která bude umět rychle
odpovídat na dotazy typu „v kolika obdélnících leží zadaný bod?“
Důležitá je přitom jak časová složitost dotazů, tak čas potřebný
na vybudování struktury.
Řešení
Konečně se podařilo poskládat jednotlivé mapy do jednoho jakž takž
použitelného celku a naplánovat záchrannou akci. Než se ale podaří
zpustošené podzemí vrátit do obyvatelného stavu, bude potřeba vybudovat
pro všechny provizorní tábor v horách.
Tiše přemýšleli, kde ve skalách vzít kousek rovné plochy. Naštěstí
sopečné tufy a popel jsou lehké, takže menší nerovnosti půjde snadno
srovnat. I tak by ale bylo milé si co nejvíc práce ušetřit. Sesedli
se okolo mapy a uvažovali nad vhodným místem.
26-4-5 Místo pro tábor (14 bodů)
Je dána výšková mapa krajiny. Terén je rozdělen na R×S
políček a pro každé z nich známe jeho nadmořskou výšku v mimozemských
pídích.
Na nějakém místě chceme postavit tábor. To obnáší vybrat obdélníkovou část
krajiny o rozměrech r×s políček a srovnat ji do roviny. Tedy přesunout
mezi těmito políčky zeminu tak, aby všechna políčka byla stejně vysoko.
Jednotky si zvolme tak, že zvýšení políčka o jednu mimozemskou píď
vyžaduje přivezení jedné mimozemské kárky zeminy.
Vaším úkolem je pro zadanou výškovou mapu a velikost tábora najít
takové místo pro tábor, abychom museli přesunout co nejméně zeminy.
Zemina je neomezeně dělitelná, ale lze ji pouze přesouvat.
Není možné ani vytvořit zeminu z ničeho, ani ji zničit.
 Lehčí varianta (za 10 bodů):
Vyřešte pro jednorozměrnou krajinu (S=s=1).
Lehčí varianta (za 10 bodů):
Vyřešte pro jednorozměrnou krajinu (S=s=1).
Řešení
Tábor utěšeně rostl. Proudili do něj stále noví členové Bratrstva,
vysvobození z čím dál vzdálenějších částí jeskynního systému. Na krajinu
se snášela další noc, mnohem optimističtější než ty předchozí.
Středu tábora vévodilo veliké ohniště, u kterého právě odpočíval Ubu
spolu s několika staršími mimozemšťany. Jacob si k nim přisedl. Chtěl
totiž využít klidné chvilky a dozvědět se něco o tom, co je Bratrstvo
zač a proč se tolik snaží svou existenci utajit.
A důvody k tajnostem skutečně existovaly: Bratrstvo organizovalo odboj
proti místnímu králi. Členové královské dynastie byli sice považováni za
potomky bohů (a dokonce prý vypadali trochu jinak než jejich poddaní), ale
vládli velmi nevybíravě a nebývale krutě.
Spiklenci už dlouho připravovali plán na svržení panovníka. Podezírali
ale krále, že o jejich úmyslech ví a že se celého Bratrstva pokusil
zbavit výbuchem sopky vyvolaným magií. Jacob se tvářil značně nedůvěřivě
– na kouzla nevěřil a ještě méně pravděpodobné bylo, že by kdokoliv na této
planetě disponoval potřebnou technikou.
Ale dost už pochybností, dnes je den mnoha šťastných shledání a takový
si zaslouží oslavu. Jacoba napadlo, že by ostatní mohl naučit nějakou
pozemskou hru. Všiml si, že sopečný tuf je natolik měkký a lehký,
že z něj jde nožem vyřezávat něco jako sněhové koule. Sice tolik nestudí,
vlastně vůbec, ale házet jdou úplně stejně. Hej! Kryj se! Pal!
26-4-6 Sněhová bitva (11 bodů)
V rovině stojí n bojovníků se sněhovými koulemi v rukou. Za chvíli začne velká řež.
Pokud bojovník A hodí kouli po bojovníkovi B, může trefit kohokoliv, kdo se
nachází na polopřímce AB.
Na vstupu dostanete polohy bojovníků v rovině. Vaším úkolem je vytvořit
datovou strukturu, pomocí které budete umět efektivně odpovídat na dotazy
„Pokud A míří na B, může zasáhnout někoho dalšího?“. Jako odpověď
stačí ano nebo ne, není potřeba hledat, koho zasáhnete.
Řešení
Do všeobecného veselí se vkrádaly stíny nedůvěry. Jak se mohl
král o existenci Bratrstva dozvědět? Není mezi nimi nějaký špión,
nebo dokonce víc takových? Královská tajná policie je přeci svými
schopnostmi po celé říši proslulá.
Jacoba napadlo, že to mohl být důvod, proč se k němu jeho někdejší
léčitelé chovali tak uzavřeně a odmítali mu odpovídat na jeho otázky.
Konec konců, královská rodina přeci má vypadat jinak než ostatní
obyvatelé planety, tak není divu, že byl Jacob krajně podezřelý.
O to víc si vážil důvěry Bratrstva.
Teď s Ubuem probírali různé hypotézy, jak by si mohli královi zvědové
předávat informace.
26-4-7 Královští špioni (9 bodů)
 Král má n špionů. Každý špion má pevně určeno, kterému jednomu
špionovi předává všechny informace, jež zjistí.
Král má n špionů. Každý špion má pevně určeno, kterému jednomu
špionovi předává všechny informace, jež zjistí.
Špionská síť s osmi špiony může například vypadat následovně:
Pokud špion dostane zprávu, kterou už zná, neposílá ji dál.
Šíření každé zprávy se tedy po konečném počtu kroků zastaví.
Váš algoritmus dostane zadanou síť špionů. Jeho úkolem je pro
každého špiona spočítat, jak dlouho bude v síti putovat zpráva,
kterou tento špion vyšle.
V síti na obrázku jednotlivé zprávy urazí postupně v pořadí dle čísla
vysílajícího špiona 5, 3, 3, 2, 5, 4, 3 a 2 kroků.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Jakmile v táboře přestala být potřeba každá pomocná ruka, Jacob dostal chuť
projít se po okolí. Chtěl si zblízka prohlédnout ztuhlé potoky lávy,
na kterých se utvořily zajímavé obrazce.
Zvolna kráčel mezi skalami a sledoval pustou krajinu. Připomněla
mu povrch Měsíce. Posmutněl, když si uvědomil, že tam už se nejspíš
nikdy nepodívá.
Najednou mu nohy uvázly v sopečném popelu. Když se je pokusil vyprostit,
jenom se propadl o něco hlouběji. Zjevně narazil na jámu plnou popela.
Marně se pokoušel rukama zachytit okraje. Sjížďěl čím dál rychleji.
„Už zase!“ blesklo mu hlavou.
Proletěl jakousi šikmou chodbou a přistál na podlaze nevelké jeskyně.
Všude se válely podivné kovové krabice. Značně omšelé a propojené
zašlými zkroucenými kabely. Na nejbližší z nich zahlédl kovový
štítek s nápisem.
Stálo na něm: „Made in China.“ Uhhh…
Pokračování příště…
O Jacobových příhodách na vzdálené planetě vyprávěl
Martin „Medvěd“ Mareš
26-4-8 Dlaždičky (16 bodů)
 V naší zoo výpočetních modelů jsme zatím potkávali volně pasoucí se exempláře.
Dnes uvidíme první zdi. Není to ovšem proto, že by náš model potřeboval chránit
před větry dešti, nýbrž proto, že tyto zdi bude náš program obkládat dlaždicemi.
V naší zoo výpočetních modelů jsme zatím potkávali volně pasoucí se exempláře.
Dnes uvidíme první zdi. Není to ovšem proto, že by náš model potřeboval chránit
před větry dešti, nýbrž proto, že tyto zdi bude náš program obkládat dlaždicemi.
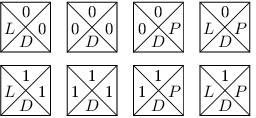
Pojďme si nejprve říct, co je to taková dlaždice. Dlaždice představuje čtverec
jednotkové velikosti, který má každou hranu obarvenou nějakou barvou.
Obarvení jednotlivých hran může a nemusí být stejné, ale každá hrana musí být
obarvena právě jednou barvou. Dohodněme se také, že barvy budeme označovat
nějakými symboly, typicky čísly a písmeny.
Často budeme pro názornost dlaždice zobrazovat opravdu jako čtverce rozdělené
na čtyři části, ale formálně dlaždici zavedeme jako uspořádanou čtveřici (ℓ, h, p, d),
kde jednotlivé symboly ℓ, h, p, d označují po řadě obarvení levé, horní, pravé
a dolní hrany dlaždice.
Z takových dlaždic můžeme skládat dláždění. Prostoru, který chceme dlaždičkovat,
říkejme zeď. Ta je obdélníková a má rozměry r ×s (přičemž
jednotkou bude délka hrany dlaždice).
Okraje zdi jsou rozděleny na úseky o jednotkové délce, a každý
z těchto úseků má podobně jako hrany dlaždic nějaké obarvení.
Jako dlaždění označujeme pokrytí zdi dlaždicemi, pokud toto pokrytí splňuje
několik podmínek. V první řadě požadujeme, aby v každém z r ×s čtverců
byla umístěna právě jedna dlaždice. Dále každé dvě sousední dlaždice musí mít
ty hrany, kterými se dotýkají, obarvené stejnou barvou. Požadavek na stejnou
barvu máme i na okrajové dlaždice, tedy dlaždice, které přiléhají k okraji zdi,
musí mít příslušnou hranu obarvenou stejnou barvou, jakou je obarvený příslušný
úsek okraje. Poslední podmínka, dlaždice nesmíme při tvorbě dláždění otáčet.
Dodejme ještě, že každou dlaždici smíme použít libovolně-krát.
Pomocí dláždění, resp. jeho existence nebo neexistence, můžeme snadno rozhodovat
úlohy, na které se odpovídá ano, nebo ne. Jak to uděláme? Musíme sestavit vhodnou
množinu dlaždic, z kterých budeme smět vybírat při tvorbě dláždění. Horní okraj zdi
obarvíme podle vstupu. Ještě potřebujeme obarvit ostatní okraje, s tím, že všechny
jejich úseky obarvíme stejnou barvou (můžeme o tom tedy uvažovat jako o obarvení
celého okraje jednou barvou). Dlaždice a obarvení vybíráme tak, aby dláždění
existovalo, právě když odpověď na úlohu je ano.
Možných dláždění (a jim příslušných množin dlaždic a obarvení okrajů) může existovat
velmi mnoho, tak si je alespoň trochu omezme. Požadujeme, aby zeď byla vždy
široká právě tak, jak dlouhý je vstup. Horní okraj tedy bude vstupu přesně
odpovídat. Navíc chceme, aby výška zdi byla nejmenší možná.
To, co jsme před chvilkou popsali, je dlaždicový program. Ten se skládá
z nějaké konečné množiny dlaždic a nějakého obarvení okrajů zdi. Formálně by se jednalo
o uspořádanou čtveřici (D, ℓ, p, d), kde D je množina dlaždic a ℓ, p, d
představují obarvení levého, pravého a dolního okraje.
Program na zadaný vstup odpoví ano, pokud je možné vydláždit nějakou zeď
dlaždicemi z množiny D tak, aby horní okraj byl obarven podle vstupu
a zbývající okraje barvami ℓ, p a d. Neexistuje-li žádné takové
dláždění, výstupem programu je ne.
Dlaždicové programy jsou chráněná zvířátka, a tak jim budeme na vstupu předkládat
pouze neprázdné řetězce.
Bývá hezké umět u programů ve výpočetním modelu určovat složitost. U dlaždicových
programů to zvládneme jednoduše: za dobu výpočtu prohlásíme minimální výšku zdi,
pro kterou existuje dláždění (časová složitost je pak maximum z dob výpočtu přes všechny
vstupy dané délky), použitou paměť pak představuje plocha vydlážděné zdi.
Vstupy, na něž je odpověď ne, takže žádné dláždění neexistuje, složitost neovlivní.
Dost bylo teoretizování, pojďme se podívat, jak se náš model návštěvníkům
předvede.
Mějme na vstupu nějakou posloupnost nul a jedniček. Naším úkolem je rozhodnout,
jestli je tato posloupnost konstantní, tedy zda obsahuje pouze nuly nebo pouze
jedničky. Využijeme k tomu dlaždicový program s následujícími dlaždicemi. Můžeme je rozdělit do čtyř typů, každý typ existuje ve
dvou barvách:
Levý okraj obarvíme L, pravý P, dolní D. Náš program určitě odpoví správně,
a dokonce mu k tomu bude stačit jeden řádek. Takové odvážné tvrzení by se ale
slušelo dokázat.
Jelikož všechny dlaždičky mají dolní hranu obarvenou D a žádná nemá barvou D
obarvenou hranu horní, buď bude mít dláždění výšku 1, nebo vůbec nepůjde vytvořit.
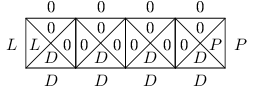
Pro konstantní posloupnost jistě dláždění existuje. V případě jednoprvkové posloupnosti
použijeme příslušnou dlaždici čtvrtého typu, v případě posloupnosti delší pomocí vhodné
dlaždice prvního typu „zvolíme číslo“ a následně ho „propagujeme“ až
k pravému okraji:
Platí i to, že vše, pro co dláždění existuje, musí být konstantní posloupnost. K levému
i k pravému okraji může přiléhat vždy jen jedna konkrétní dlaždice (podle hodnoty na vstupu),
a k jejich spojení je potřeba „předávat“ stále stejné číslo.
Úkol 1 [3b]
Sestavte dlaždicový program, který o posloupnosti nul a jedniček na vstupu zjistí,
zda je v ní počet jedniček dělitelný třemi.
Úkol 2 [2b]
Mějme nějaký dlaždicový program, který pracuje v čase t, kde t je konstanta.
Dokažte, že existuje jiný dlaždicový program, který odpovídá na tutéž otázku,
ale stačí mu čas 1.
Závorkování nás stále baví
V jednotlivých dílech seriálu jste si mohli zkoušet v různých výpočetních modelech
ověřovat, že zadaná posloupnost je správně uzávorkovaná. Toho jsou schopné i dlaždicové
programy, a na rozdíl od počítadlových strojů z minulého dílu jim ani nemusíme
posloupnost nějak speciálně kódovat.
Úkol 3 [4b]
Sestavte dlaždicový program, který o posloupnosti otvíracích a zavíracích závorek
na vstupu rozhodne, zda je správně uzávorkovaná.
Úkol 4 [3b]
Dokažte, že rozhodnutí uzávorkování nelze pomocí dlaždicových programů dosáhnout
v lepší než logaritmické časové složitosti. Kdybyste si nevěděli rady, zkuste
alespoň dokázat, že konstantní čas nestačí.
Příbuzní Turingových strojů?
Když jsme se na začátku seriálu zastavili u Turingových strojů, nepřečetli jsme
si jednu ceduli o jejich příbuzných.
Připomeňme si, že stroj se v každém kroku výpočtu rozhoduje podle stavu, ve kterém
se právě nachází, a podle znaku na aktuálním políčku pásky. A každé kombinaci
stavu a znaku jeho program přiřadí instrukci, která se má provést. Instrukce říká, co má
stroj dál udělat (na jaký znak přepsat aktuální část vstupu, kam se posunout, do jakého přejít
stavu). Ke každé kombinaci stavu a znaku jsme měli právě jednu možnost.
Ale co kdyby těch možností bylo víc? Co kdybychom jedné kombinaci stavu a
vstupu přiřadili hned několik možných reakcí? Přesně tak to totiž mají nedeterministické
Turingovy stroje. Jak si ale takový stroj z možných reakcí vybere tu, kterou
doopravdy provede?
Jedna možnost je představit si, že nedeterministický stroj umí vracet svůj
výpočet. Pak můžeme říct, že nedeterministický stroj v každém kroku výpočtu
vykoná první nevyzkoušenou možnou reakci (nevyzkoušenou v daném kroku) a pokračuje dál.
Pokud se někdy dostane do stavu, kdy už nemá další možné reakce, nebo do koncového
stavu ne, jednoduše vrací svůj výpočet až do toho kroku, kdy měl naposledy na výběr.
Teprve v případě, že se vrátí do počátečního stavu a už nemá co vyzkoušet, zapíše
ne.
Nebo si můžeme představit, že je stroj vybaven křišťálovou koulí (neboli orákulem),
které mu pokaždé poradí takovou reakci, aby na konci výpočtu stroj odpověděl ano.
Jen pokud taková posloupnost rad neexistuje, odpověď zní ne.
Úplně mimo ale není ani představa, že v každém kroku se vesmír rozštěpí na tolik kopií,
kolik má nedeterministický Turingův stroj právě možností, v každém ze vzniklých vesmírů
se provede jedna reakce a výpočet pokračuje dál. Důležité pro nás je, jestli alespoň
v jednom vesmíru dojde stroj do stavu ano.
Úkol 5 [4b]
Dokažte, že dlaždicové programy jsou ekvivalentní nedeterministickým Turingovým strojům
pracujícím v lineárním prostoru. Tedy máte za úkol dokázat, že jakýkoli
nedeterministický Turingův stroj, který má lineární prostorovou složitost, lze
reprezentovat jako dlaždicový program, a naopak, každý dlaždicový program (při našich
omezeních na rozměry zdi) lze reprezentovat jako nedeterministický Turingův stroj
pracující v lineárním prostoru.
Prozradíme vám malou nápovědu k předchozímu úkolu: tvrzení stačí dokázat o Turingových
strojích pracujících v prostoru přesně n (kde n je velikost vstupu). Pokud totiž
stroj používá prostor cn pro nějakou konstantu c>1, můžeme podobně jako v úkolu 2
vytvořit jiný stroj, kterému bude stačit prostor n.
Karolína „Karryanna“ Burešová
Řešení
 Lehčí varianta (za 4 body):
Rozmyslete si, jak úloha dopadne pro dvě hromádky. Své tvrzení dokažte.
Lehčí varianta (za 4 body):
Rozmyslete si, jak úloha dopadne pro dvě hromádky. Své tvrzení dokažte. V rovině je položeno několik kusů mapy. Kusy mají tvar obdélníků
se stranami rovnoběžnými s osami souřadnic.
V rovině je položeno několik kusů mapy. Kusy mají tvar obdélníků
se stranami rovnoběžnými s osami souřadnic. Král má
Král má 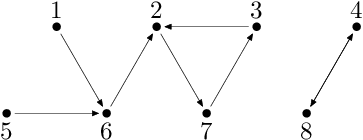
 V naší zoo výpočetních modelů jsme zatím potkávali volně pasoucí se exempláře.
Dnes uvidíme první zdi. Není to ovšem proto, že by náš model potřeboval chránit
před větry dešti, nýbrž proto, že tyto zdi bude náš program obkládat dlaždicemi.
V naší zoo výpočetních modelů jsme zatím potkávali volně pasoucí se exempláře.
Dnes uvidíme první zdi. Není to ovšem proto, že by náš model potřeboval chránit
před větry dešti, nýbrž proto, že tyto zdi bude náš program obkládat dlaždicemi.