Pátá série dvacátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 27-5-1: Šíření poplašné zprávy
- 27-5-2: Survivalisté
- 27-5-3: Čekání na poště
- 27-5-4: Školení zaměstnanců
- 27-5-5: Kniha přání a stížností
- 27-5-6: Autobazar
- 27-5-7: Shellová automatizace
 27-5-1 Šíření poplašné zprávy (Zadání)
27-5-1 Šíření poplašné zprávy (Zadání)
K postavení rychlého řešení si připomeneme něco o stromech. Kdybychom volali jenom do jedné kanceláře, hledali bychom střed stromu: vrchol, který má maximální vzdálenost do jiných vrcholů nejmenší. Poloměr stromu je „poloměr kružnice opsané“: největší vzdálenost mezi středem stromu a jinými vrcholy. Strom obsahuje jednu nebo více nejdelších cest. Nejdelší cesta jde najít v lineárním čase například některým z postupů v řešení úlohy 12-1-2. Prostřední vrchol nejdelší cesty je střed stromu a poloměr stromu je polovina délky nejdelší cesty. (Pokud má nejdelší cesta liše hran, je poloměr ta větší polovina a střed není jednoznačný.)
Představme si teď, že ty dva vrcholy, do kterých je nejlepší zatelefonovat, už známe, a označme je jako a a b. Rozdělíme si vrcholy stromu na dva sektory Sa a Sb podle toho, ze kterého z vrcholů a, b dorazí signál dříve. Pokud někam dorazí z obou směrů zároveň, patří daný vrchol do obou sektorů. Místo, kde se sektory poprvé potkají, je buď společný vrchol, nebo jedna hrana.
Na následujícím obrázku je příklad rozdělení stromu na sektory s poloměry 2 a 3. Při takovémto rozdělení se poplašná zpráva rozšíří za 3 jednotky času. Snadno si rozmyslíte, že lépe to nejde. Přestože sektory mají složitější průnik, na nejdelší cestě (vodorovné) z něj najdete jen jediný bod (označen čtverečkem). Právě tomu budeme říkat hraniční bod. Kdybychom místo vrcholu b vyslali signál z jeho pravého souseda, dostaneme stejně dobré řešení, ale hranici mezi sektory bude tvořit hrana nejdelší cesty.

Ukážeme si nejdřív pomocné tvrzení: když si vybereme nějakou nejdelší cestu, pak v některém optimálním řešení na této nejdelší cestě leží hranice sektorů.
Poloměr Sa i Sb musí být nejvýše stejný jako poloměr celého stromu. V případě, že některý ze sektorů má stejný poloměr jako celý strom, tak víme, že optimální řešení by kromě zvoleného {a,b} bylo například zavolat do středu celého stromu a jednoho z konců nejdelší cesty. Když si zvolíme tenhle pár kanceláří, dostaneme optimální řešení, ve kterém na zvolené nejdelší cestě leží hranice sektorů.
Když jsou poloměry Sa i Sb ostře menší než poloměr celého stromu, pak nemůže celá naše nejdelší cesta ležet uvnitř jednoho sektoru: nevešla by se tam, protože sektory mají menší poloměr než celý strom. Nejdelší cesta tedy leží v obou sektorech, a proto obsahuje jejich hranici.
Když teď víme, že na libovolné nejdelší cestě leží hranice optimálních sektorů, nějakou nejdelší cestu si vybereme a hranici tam zkusíme najít. Když jako hranici zkoušíme hranu, bude levý a pravý sektor tvořený půlkami stromu, které vzniknou po odebrání hrany. Když jako hranici zkoušíme vrchol, musíme se ještě rozhodnout, co uděláme s případnými hranami do vrcholu, které nevedou po nejdelší cestě. Podstromy, do kterých tyto hrany vedou, připojíme do obou sektorů: jestli je opravdu optimální rozdělit sektory tímto vrcholem, tak signál do vrcholu dorazí z obou stran ve stejnou chvíli, a proto ve stejnou chvíli dorazí i do ostatních hran pověšených na tento vrchol.
Každý levý sektor se tedy skládá z nějakého začátku nejdelší cesty a ze všech podstromů, které na této části nejdelší cesty „visí“. Délku začátku nejdelší cesty si označme i. Pro každou hodnotu i si spočítáme poloměr příslušného levého sektoru a označíme ho jako R1[i]. Podobně pro všechny délky j pravého konce spočítáme poloměry pravých sektorů R2[j].
Když má nejdelší cesta ℓ vrcholů, projdeme všech O(ℓ) možných rozdělení na sektory a vybereme to, ve kterém bude obvolání celého stromu trvat co nejkratší čas. Dělit sektory můžeme buď v hraně, nebo ve vrcholu. Když dělíme v i-té hraně, bude nám obvolání celého stromu trvat čas max{R1[i], R2[ℓ-i+1]}, a když v i-tém vrcholu, bude to trvat čas max{R1[i], R2[ℓ-i+2]}.
Zbývá vyřešit, jak budeme počítat poloměry sektorů. Kdybychom se spokojili se složitostí O(N2), stačilo by každý poloměr spočítat v lineárním čase. My však použijeme dynamické programování a dostaneme optimální čas O(N). Postup si ukážeme na levém sektoru. Vrcholy nejdelší cesty si očíslujeme zleva doprava.
Všimneme si, že nejmenší možný sektor je list, který pod sebou nemá žádné hrany, protože bychom jinak mohli o tuto hranu protáhnout nejdelší cestu. Obecněji: když si odmyslíme hrany v nejdelší cestě, tak v podstromu pod i-tým vrcholem sektoru nesmí být větev hlubší než i. Dále si všimneme, že nejdelší cesta uvnitř sektoru vede vždycky z nejhlubší větve pod jedním vrcholem nejdelší cesty do nejhlubší větve pod jiným vrcholem nejdelší cesty.
Místo poloměru sektoru budeme udržovat délku jeho nejdelší cesty, ze které jde poloměr spočítat podělením dvěma. Dynamické programování bude postupně k sektoru přidávat segmenty, které se skládají z přidaného vrcholu nejdelší cesty a nového podstromu pod ním. Poslednímu vrcholu nejdelší cesty, který jsme do sektoru přidali, říkejme konec sektoru. Nejdříve si pro každý vrchol na nejdelší cestě předpočítáme maximální hloubku jeho podstromů (když ignorujeme hrany nejdelší cesty) a uložíme je do pomocného pole A.
Dynamické programování bude udržovat:
- M: délku nejdelší cesty v zatím prošlém sektoru.
- D: délku nejdelší cesty z konce zatím prošlého sektoru.
Po přidání nového segmentu číslo i může M buď zůstat stejné, nebo můžeme zjistit, že nejdelší cesta do nového konce sektoru zleva plus nejhlubší větev pod novým koncem sektoru tvoří delší cestu délky D+A[i]+1. Nová hodnota M tedy bude max{M, D+A[i]+1}. Nejdelší cesta z konce sektoru se buď prodlouží o jeden vrchol, nebo změní na nejhlubší cestu do stromu pověšeného pod novým vrcholem, proto D upravíme na max{D+1, A[i]}.
Náš algoritmus tedy najde nejdelší cestu, nad kterou dynamickým programováním spočítá poloměry levých a pravých sektorů, a nakonec najde nejlepší místo k rozdělení. Kanceláře, do kterých chceme poslat signál, pak můžeme dopočítat jako středy sektorů, na které strom rozdělíme. Stačí nám jen O(N) času i paměti.
 27-5-2 Survivalisté (Zadání)
27-5-2 Survivalisté (Zadání)
Zadání požaduje, aby každý člověk právě jednu věc dal jinému a alespoň jednu dostal. Ale snadno nahlédneme, že pokud jsou tyto podmínky splněny, musí každý i dostat právě jednu věc. V oběhu je N věcí (kde N je počet survivalistů), a pokud by někdo dostal dvě z nich, na jiného žádná nezbude.
Chceme tedy vybrat nějaké dvojice (dárce, příjemce) takové, že každý je právě v jedné dvojici jako dárce a právě v jedné jako příjemce. To velice připomíná problém maximálního párování v bipartitním grafu. Bez znalosti tohoto pojmu úloha příliš řešit nešla, takže pokud jej potkáváte poprvé, nahlédněte do naší Encyklopedie.
Náš graf sice není bipartitní, ale snadno z něj bipartitní vyrobíme. Od každého vrcholu (u) vyrobíme dvě kopie: jedna bude reprezentovat daného survivalistu v roli dárce (ud), druhá jako příjemce (up). Každou hranu z původního grafu povedeme z odpovídajícího dárcovského do odpovídajícího přijímajícího vrcholu – tedy z původní hrany uv vytvoříme v novém grafu hranu udvp. Tím nám přirozeně vznikne bipartitní graf s partitami dárců a příjemců.
Například z grafu v zadání:
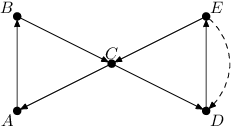
vznikne následující:
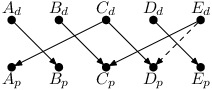
Maximální párování v tomto grafu (bez čárkované hrany) má velikost 4:
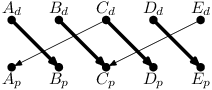
Každá hrana tohoto párování popisuje jednu předanou věc: například A předá něco B. V případě tohoto grafu požadavek ze zadání splnit nelze – E nic nedostane. Snadno si rozmyslíte, že zadání splníme právě tehdy, když jsou spárovány všechny vrcholy (takovému párování říkáme perfektní). Pokud perfektní párování existuje, určitě je maximální. Tedy není-li nalezené maximální párování perfektní, graf zadání nesplňuje.
Pokud zahrneme do vstupního grafu čárkovanou hranu, perfektní párování již existuje:
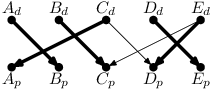
Graf s čárkovanou hranou tedy, jak už koneckonců víte ze zadání, požadavky splňuje.
Algoritmus bude vypadat tak, že v lineárním čase vytvoříme ze vstupu odpovídající bipartitní graf a spustíme na něj nějaký párovací algoritmus. Pokud je velikost nalezeného maximálního párování rovna počtu survivalistů, odpovíme „ano“, jinak odpovíme „ne“. Například při použití Hopcroftova-Karpova algoritmu dosáhneme časové složitosti O(M√N), kde M je počet hran a N počet vrcholů. Vystačíme si s lineární pamětí (O(N+M)).
Jako třešničku na dortu pro zkušenější řešitele ukážeme, že řešení pomocí párování je optimální. Použijeme k tomu stejný trik, jaký se používá při dokazování NP-úplnosti: ukážeme, že lze problém perfektního párování v bipartitním grafu převést na řešení naší úlohy.
Předpokládejme, že máme zadaný nějaký bipartitní graf, ve kterém chceme najít perfektní párování (resp. ověřit jeho existenci). Aby to mělo smysl, musí být obě partity stejně velké. Naším úkolem je sestrojit z něj takový vstup pro Survivalisty, který bude korektní právě tehdy, když původní graf má perfektní párování.
To je ale jednoduché: každou hranu zorientujeme z horní partity do dolní, a navíc přidáme „zpětné hrany“, které povedou vždy z i-tého vrcholu dolní partity do i-tého vrcholu horní. Například z grafu (zvýrazněno perfektní párování)
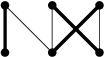
vznikne vstup (zvýrazněna korektní množina předání)
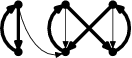
Nyní si snadno rozmyslíte obě implikace. Pokud existuje perfektní párování, snadno z něj utvoříme řešení Survivalistů: použijeme párovací hrany a všechny zpětné. Naopak každé korektní řešení Survivalistů musí nutně použít všechny zpětné hrany (z libovolného vrcholu dolní partity vede jen jedna hrana – zpětná – takže musí být použita), jejich odebráním dostaneme perfektní párování.
Tím jsme ukázali, že libovolný algoritmus řešící naši úlohu můžeme použít jako trochu zvláštní párovací algoritmus: připravíme mu vstup se zpětnými hranami (to zvládneme v lineárním čase, který můžeme zanedbat, neboť lineární čas potřebujeme i na pouhé načtení vstupu), zeptáme se na řešení a víme, zda původní graf obsahoval perfektní párování. Tedy žádné řešení Survivalistů nemůže být rychlejší než nejrychlejší algoritmus, který umí rozhodnout o existenci perfektního párování v bipartitním grafu, protože bychom pomocí něj uměli vytvořit rychlejší párovací algoritmus, což je ve sporu s tím, že ten původní byl nejrychlejší.

 27-5-3 Čekání na poště (Zadání)
27-5-3 Čekání na poště (Zadání)
Nejprve si úlohu trochu zjednodušíme. Budeme uvažovat frontu lidí skutečně jako frontu a ne jako uzavřený okruh. Naším úkolem tedy bude pospojovat body v rovině lomenou čarou tak, aby se nikde neprotínala. Toho můžeme docílit jednoduše tím způsobem, že si body seřadíme podle y-ové souřadnice (v případě rovnosti pak podle x-ové).
Tento setříděný seznam bude přesně popisovat pořadí bodů, ve kterém je bude lomená čára procházet. Nikde se neprotne, neboť každá úsečka je ve všech bodech níže než ta předchozí (v případě dvou bodů se stejnou y-ovou souřadnicí je celá napravo).
Jak nám toto pozorování pomůže k vyřešení původní úlohy? Určitě nebude stačit body vypsat v setříděném pořadí, protože pak by nám mohla poslední úsečka spojující první a poslední bod protínat nějaké předchozí. Dobrým trikem ale je rozdělit si body na dvě části a tyto dvě části vyřešit předcházejícím algoritmem. V jedné části začneme od nejvýše položeného bodu a postupně budeme klesat až do nejnižšího bodu (tato část bude tvořit jakousi „levou polovinu“ mnohoúhelníka). Ve druhé části naopak začneme od nejníže položeného bodu a postupně budeme po zbylých bodech stoupat, až se opět dostaneme k výchozímu, nejvýše položenému bodu (tato lomená čára bude tvořit „pravou polovinu“ mnohoúhelníka). Budeme tím pádem chtít, aby každý bod byl v právě jedné části, s výjimkou nejvýše a nejníže položeného bodu, které můžeme pomyslně zařadit do obou částí.
Musíme ještě body do těchto dvou částí rozdělit. Potřebujeme, aby se úsečky z jedné části nekřížily s těmi z části druhé. Jedno řešení je přijít s nějakou přímkou a body nalevo od této přímky přiřadit do první části a body napravo do druhé. Toto nám zaručí, že žádná část lomené čáry nepřekročí tuto rozdělující přímku, a tím spíš se nebude křížit s žádnou částí druhé lomené čáry. Jelikož chceme nejvyšší a nejnižší bod v obou těchto částech, nabízí se vzít právě přímku určenou těmito dvěma body.
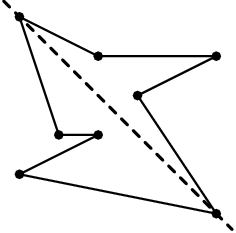
Pro určení, na které straně přímky bod leží, stačí vzít determinant matice, jejíž první řádek je směrový vektor naší rozdělující přímky a druhý řádek je vektor určený nejnižším bodem a zkoumaným bodem. Podle znaménka tohoto determinantu pak můžeme určit, na které straně se zkoumaný bod nachází. Pokud nám to nevěříte, tak nahlédněte do naší geometrické kuchařky, kde naleznete podrobnější popis.
Celkovým výstupem algoritmu bude seznam bodů v setříděném pořadí nejprve z jedné části a pak z druhé. Nesmíme ale zapomenout na to, že náš původní algoritmus obě části seřadil odshora dolů, chceme tedy jednu z částí vypisovat v opačném pořadí.
Jak je to s časovou a paměťovou složitostí? Setřídění prvků zvládneme v čase O(N log N). Roztříděním do dvou částí strávíme na každém bodě konstantní čas, tedy dohromady O(N), a samotné vypsání pak stihneme také v lineárním čase. Takže celková časová složitost je O(N log N). Pamatovat si musíme pouze body na vstupu, takže si vystačíme s lineární pamětí.
 27-5-4 Školení zaměstnanců (Zadání)
27-5-4 Školení zaměstnanců (Zadání)
V zadání jste dostali pěkně zakořeněný strom, to přímo vybízí k tomu ho nějak prohledat. Ukážeme si řešení využívající prohledání do hloubky.
Máme-li podstrom hloubky ostře menší než K, žádný vyškolený zaměstnanec v něm zatím být nemusí. Jakmile ale dostaneme podstrom s hloubkou právě K, už v něm nějakého zaměstnance vyškolit musíme – z vyšších pater stromu už bychom nedosáhli do listů tohoto podstromu. Vhodným kandidátem je kořen právě prozkoumávaného podstromu, žádný jiný vrchol nemusí dosáhnout do všech větví.
Kdybychom pouze takto odřezávali podstromy, nemusí nám vyjít správné řešení, protože ignorujeme dosah zaměstnance nahoru po stromě. Myšlenku si tedy zobecníme a zavedeme si u každého vrcholu vyškolenost.
Vyškolenost zaměstnance, kterého na školení pošleme, bude K. Směrem od něj se bude vyškolenost snižovat. Všimněte si nyní, že řešení splňující podmínky musí mít na konci v každém vrcholu vyškolenost alespoň nula.
Nastavíme vyškolenost listů na nulu a budeme konstruovat řešení rekurzivně pro vnitřní vrcholy. Na chvíli si dovolíme, aby vyškolenost klesla u některých vrcholů do záporných čísel, a teprve až bude příliš nízká, tak ji spravíme vyškolením zaměstnance v kořeni.
Jak tedy spočítáme vyškolenost vnitřního vrcholu? Podíváme se na minimum a maximum vyškoleností synů. Pokud má některý ze synů vyškolenost tak vysokou, že pokryje nedostatky ostatních synů (max + min > 0), můžeme vyškolenost aktuálního vrcholu nastavit na max - 1 a tím je celý podstrom vyřešen.
Jinak musíme respektovat nejméně vyškoleného syna. Pokud je min = -K, pak nezbývá než poslat na školení aktuální vrchol, a tím všechny syny spravit (vyškolenost bude K). Jinak vrátíme min - 1 a odložíme vyřešení na později.
Z této úvahy se vymyká již jen kořen celého stromu, kde nelze řešení odkládat. Proto jej na konci přidáme, pokud musíme. Minimalita nalezeného řešení vychází z úvahy ve druhém odstavci.
Algoritmus poběží v lineárním čase k počtu vrcholů, stejně tolik spotřebuje paměti. Jen pozor, Python při přímočaré implementaci rekurzí příliš plýtvá místem na zásobníku pro volání funkce, proto v něm úloha byla řešitelná, pouze pokud jste použili explicitní zásobník jen na vrcholy a rekurzi jste se vyhnuli.
 27-5-5 Kniha přání a stížností (Zadání)
27-5-5 Kniha přání a stížností (Zadání)
V úloze je nutné ve vstupním textu hledat výskyty různých slov, navíc byla úloha v letáku označena jako kuchařková. Jak jste někteří sami zformulovali, to přímo vybízí k použití Aho-Corasickové.
Ale teď jak ji použít. Předně, můžeme si ji trochu zjednodušit: jelikož slova nejsou svými sufixy, nemusíme vůbec řešit zkratky.
Naivní řešení může pomocí Aho-Corasickové hledat výskyt libovolné jehly (tedy libovolného zakázaného slova) v celém vstupu. Kdykoliv nějakou najde, smaže ji a hledání se opět spustí od začátku. To je zaručeně správný postup, ovšem běží v O(S2), kde S značí délku vstupu. Přitom řetězcové úlohy se, zejména v soutěžích, obvykle dají řešit lineárně.
Můžeme si rozmyslet, že stačí vracet se ve vstupním řetězci ne na začátek, ale pouze o délku nejdelší jehly. Delší jehlu jsme vytvořit nemohli, a kdyby se nějaká v řetězci už vyskytovala, našli bychom ji dřív, než bychom došli k aktuálnímu znaku. Tím jsme se sice z O(S2) dostali na O(S · jmax), nicméně to stále není lineární.
Hlavní problém naivního řešení je, že spoustu věcí zbytečně počítá opakovaně. Náš průchod automatem (resp. trií) bude v té části řetězce, která se nezměnila, stále stejný. Pokud jsme při zpracování řetězce došli na pozici i, a tím se dostali do vrcholu v, i když smažeme nějaké znaky i+1, …, i+j a vrátíme se v řetězci na začátek, stejně na pozici i zase skončíme ve vrcholu v.
Kdybychom tedy věděli, v jakém vrcholu jsme na pozici i byli, můžeme se po smazání jehly začínající na pozici i+1 prostě „přepnout“ do daného vrcholu a nerušeně pokračovat ve zpracovávání řetězce. To zvládneme snadno, stačí nám pořídit si pole, do kterého si pro každou pozici uložíme odpovídající vrchol trie.
Jeden problém jsme tím ovšem vyrobili. Přesněji řečeno jsme si rozbili časovou složitost. Původní argument pracuje s tím, že při načtení znaku se sice můžeme vracet o mnoho vrstev trie nahoru, ale nemůžeme se celkem vracet vícekrát, než kolikrát jsme sestoupili níž. A protože při přečtení znaku sestoupíme maximálně o jednu vrstvu, bude i návratů nejvýš lineárně.
Jenže přepínáním stavů se za každý načtený znak můžeme přesunout o mnohem víc vrstev dolů, a tedy i těch návratů může být mnohem víc. Hodilo by se nám proto přímo vědět, ve kterém stavu se vracet přestaneme a budeme moci zase přejít o úroveň níž.
To si (alespoň pro rozumně velkou abecedu) můžeme předpočítat. Musíme to ale udělat šikovně. Půjdeme na to opět po vrstvách. Začneme s kořenem, pro ten je to jednoduché – pro každý znak abecedy buď vede hrana někam dolů, nebo zůstáváme v kořeni.
Pro každý další vrchol v a každý další znak abecedy z pak bude platit, že buď z v existuje hrana dolů označená z, nebo se vracíme tam, kam bychom při čtení z došli z toho vrcholu u, do kterého vede zpětná hrana z v. Protože postupujeme po vrstvách, to, kam bychom při čtení z došli z u, už určitě víme. Zpracování každé dvojice vrchol a znak tak zabere jen konstantní množství času, dohromady tedy O(J · |Σ|). Časovou složitost konstrukce trie jsme si tedy nezhoršili.
Návraty v trii nahoru jsme vyměnili za konstantní přepnutí stavu. Sestupů dolů bude maximálně lineárně, protože při přečtení znaku se stále posuneme maximálně o jednu úroveň níž. Celková velikost výstupu (toho, co nám bude Aho-Corasicková postupně vracet) bude díky mazání již nalezených jehel maximálně S. Hledání samo o sobě tedy zabere O(S).

Zbývá rozmyslet si, kolik času nám zabere samotné smazání jehly ze vstupu. Tady totiž záleží, jak se rozhodneme se vstupem pracovat. Pokud si ho uložíme do pole, narazíme na to, že mazání v poli je obecně drahé – přinejhorším lineární. Asi nejpříjemnější řešení je pořídit si ještě druhé pole, v kterém budeme postupně vytvářet výstup. Při zpracování znaku ho zkopírujeme do výstupního pole, při mazání jehly ji mažeme právě z výstupního pole.
Tím vždy mažeme z konce, tedy smazání znaku je konstantní, smazání jehly lineární v její délce. A protože nemůžeme smazat víc znaků, než jsme jich na vstupu dostali, zaberou všechna mazání dohromady maximálně O(S). Celý algoritmus tak poběží v čase O(S + J · |Σ|) a spotřebuje stejné množství paměti.
Pro úplnost dodejme, že kdyby byla abeceda příliš velká na předpočítání, můžeme návraty počítat „za běhu“. Stavy, do kterých se přepínat, si můžeme ukládat do binárního stromu stejně jako stavy, do kterých vedou běžné hrany dolů. Při načtení znaku se podíváme, zda už máme stav spočítaný, a pokud ne, spočítáme ho (a při návratu z výpočtu uložíme přepínaný stav i všem vrcholům, přes které jsme prošli). Přepnutí stavu bych pak bylo O(log |Σ|), celková složitost O((S+J) log |Σ|).
 27-5-6 Autobazar (Zadání)
27-5-6 Autobazar (Zadání)
Nejprve uveďme na pravou míru pár nešťastných formulací ze zadání, které tiskařský šotek propašoval několika koly korektur a které se naštěstí ujasnily v diskusi ve fóru. Číslo vyjadřující počet aut se pochopitelně do paměti vejde (jinak by úloha vůbec nebyla řešitelná). To, co se nevejde, je libovolná datová struktura obsahující všechna auta nebo všechny jejich barvy. Celkově smíme používat jen konstantně velkou paměť, ovšem neměříme ji v bitech. Jako jednotku prostorové složitosti používáme zde, jakož i jinde v KSPčku, čísla velká srovnatelně s těmi ze vstupu (případně polynomiálně větší). Za zmatky se každopádně omlouváme.
Binární vyhledávání
Úkolem je najít v posloupnosti n čísel takové, které se vyskytuje více než (n/2)-krát. Takovému číslu budeme říkat vítěz.
Náš první algoritmus na nalezení vítěze bude založený na binárním vyhledávání. Začneme tím, že spočítáme minimum a maximum ze zadaných čísel, označíme si je třeba m a M. Pak interval mezi nimi rozdělíme na poloviny a pro každou z polovin spočítáme, kolik čísel se v ní vyskytuje. Pokud existuje vítěz, pak ta z polovin, v níž leží, musí obsahovat aspoň n/2 čísel. Tuto polovinu opět rozdělíme na poloviny a tak dále, až interval omezíme na jedinou hodnotu.
Celkem provedeme O(log(M-m)) kroků, každý z nich jednou přečte celý vstup. Celý algoritmus tedy běží v čase O(n · log(M-m)).
Hlasování o číslicích
Jiný způsob s podobnou časovou složitostí je založený na následující úvaze: Kdyby byla všechna čísla řekněme dvojciferná a vítězem bylo číslo 42, pak nadpoloviční většina čísel musí začínat čtyřkou (tou začínají všechny výskyty vítěze a možná ještě nějaká další čísla). Podobně musí nadpoloviční většina končit dvojkou.
Můžeme si tedy všechna čísla rozložit na číslice v desítkovém zápisu a uspořádat hlasování o nejpopulárnější číslici. To pro každou pozici trvá O(n) a pozic je celkem O(log M).
Pakliže vítěz existuje, musí být tvořen odhlasovanými číslicemi. Pozor ale na to, že i ve vstupu bez vítěze může na každé pozici mít nějaká číslice nadpoloviční většinu – triviální příklad je třeba vstup 12, 13, 23. Odhlasované číslo je tedy potřeba dodatečně ověřit.
Tento algoritmus má složitost O(n · log M). Dodejme ještě, že implementaci by zjednodušilo, kdybychom použili místo desítkové soustavy dvojkovou.
Optimální řešení
Všechny tyto úvahy o číslech nás ale od optimálního řešení spíš odvádějí. Zapomeňme na to, že barvy aut mají nějakou strukturu, a považujme je za něco, co lze jenom porovnávat na rovnost. Tím jsme algoritmu dovolili v zásadě jen pamatovat si nějakých konstantně mnoho barev (víc se nám do paměti nevejde) a počítat, kolikrát se vyskytly. To nás dovede k překvapivě jednoduchému řešení.
V každém okamžiku si budeme pamatovat jednu barvu, té budeme říkat kandidát, a udržovat si počítadlo výskytů této barvy.
 Na počátku výpočtu se kandidátem stane první prvek vstupu a počítadlo
nastavíme na jedničku. Kdykoliv pak narazíme na další výskyt téže
hodnoty, počítadlo o jedna zvýšíme. Pokud na výskyt jakékoliv jiné
barvy, počítadlo o jedničku snížíme. A pokud počítadlo klesne na nulu,
zapomeneme na všechno, co jsme viděli, a prohlásíme za kandidáta
bezprostředně následující prvek.
Na počátku výpočtu se kandidátem stane první prvek vstupu a počítadlo
nastavíme na jedničku. Kdykoliv pak narazíme na další výskyt téže
hodnoty, počítadlo o jedna zvýšíme. Pokud na výskyt jakékoliv jiné
barvy, počítadlo o jedničku snížíme. A pokud počítadlo klesne na nulu,
zapomeneme na všechno, co jsme viděli, a prohlásíme za kandidáta
bezprostředně následující prvek.
Tvrdíme, že existuje-li vítěz, je roven tomu kandidátovi, který nám zbyl na konci výpočtu.
Jakmile dokážeme, že je to pravda, bude algoritmus hotový: prvním průchodem budeme počítat kandidáty, druhým průchodem ověříme, že finální kandidát je skutečně vítězem. To zabere čas O(n) a konstantní prostor (stačí nám čtyři proměnné: aktuální prvek, kandidát, počítadlo a celkový počet prvků).
Pro potřeby důkazu rozdělíme vstup na epochy. Epocha skončí buďto vynulováním počítadla, nebo tím, že dojde vstup. Například takto:
První prvek epochy se stane kandidátem a zůstává jím až do konce epochy. Pro každou epochu kromě poslední platí, že počet zvýšení počítadla se musel rovnat počtu snížení, takže kandidát je roven právě polovině prvků v epoše. Jen poslední epocha může končit kladnou hodnotou počítadla, takže kandidát se v ní může vyskytovat vícekrát než ostatní prvky.
Teď už si stačí všimnout, že pokud je nějaký prvek vítězem, musí se vyskytovat v nadpolovičním počtu případů v alespoň jedné epoše. Už ale víme, že prvek s touto vlastností může ležet pouze v poslední epoše a musí to být její kandidát. Hotovo.
 27-5-7 Shellová automatizace (Zadání)
27-5-7 Shellová automatizace (Zadání)
Podúloh v tomto díle seriálu bylo mnoho, pojďme se do nich pustit popořadě.
Úkol 1 – Počítání řádek v souborech
Tento úkol měl vlastně dva jednoduché kroky: prvním z nich bylo získat všechny
soubory s příponou .txt a pak je vhodným způsobem poslat do příkazu
wc a nechat spočítat řádky v nich.
V podstatě tedy šlo jen o zavolání příkazů find a přes xargs
příkazu wc. Nakonec se ještě pomocí tail a awk dalo
z výstupu wc vyseknout jen celkový součet na posledním řádku:
find . -name "*.txt" -print0 | xargs -0 wc -l
| tail -n1 | awk '{print $1}'
Úkol 2 – Hledání prázdných podadresářů
Při zadávání tohoto úkolu jsme si neuvědomili, že samotný find má přepínač
-empty a stačilo tak pouze zavolat následující příkaz (-mindepth
je zde z důvodu, aby nebyl vypsán i aktuální adresář, kdyby byl prázdný):
find . -mindepth 1 -type d -empty
Naše původní (a výrazně pomalejší) řešení spočívalo v tom, že si necháme vypsat
příkazem find všechny složky a jednu po druhé budeme testovat jejich
prázdnost (třeba podle toho, jestli ls -A něco vypíše):
find -mindepth 1 -type d | while read -r dir; do
[ -z "$(ls -A "$dir")" ] && echo "$dir";
done
Úkol 3 – Změna přípony
Úkolem bylo změnit všechny přípony .tvuj na .muj, na první pohled
jednoduchá práce. Nalezení všech souborů, jichž se to týká, je už jen jednoduché
použití známého příkazu find, změna přípony je ale záludnější.
Kdyby šlo pouze o to příponu přidat, bylo by to jednoduché použití mv
ve stylu mv "$0" "$0.muj". Ale takto je to o trochu složitější.
Zde se hodí zmínit expanzi a substituci v proměnných, o které v seriálu
zmínka nepadla. Pokud napíšeme ${promenna%.txt}, tak dostane obsah
proměnné oseknutý o koncové .txt. Bez tohoto by nový název souboru šel
zkonstruovat třeba voláním subshellu (pomocí `...` nebo $(...))
a v něm příkazu sed. Ve vzorovém řešení níže ale použijeme kratší zápis.
Pokud bychom dostali název souboru v proměnné $0, vypadal by pak příkaz
jako níže (uvozovky jsou tam třeba kvůli mezerám v názvech souborů):
mv "$0" "${0%.tvuj}.muj"
Když budeme příkaz dávat do -exec části příkazu find, musíme ještě
navíc udělat jeden trik. Samotný find nám žádnou proměnnou, na které by
se dala provádět tato expanze, neposkytne, ale můžeme si zavolat shell, kterému
hodnotu od findu předáme jako první parametr a pak ji budeme mít uvnitř
dostupnou právě jako proměnnou $0:
sh -c 'mv "$0" "${0%.tvuj}.muj"' "{}"
Poslední záludnou věcí, na kterou se hodí pamatovat, je to, že na .tvuj
může končit i jméno adresáře a ten bychom měli také přejmenovat. Ale když to
uděláme dříve, než přejmenujeme soubory v tomto adresáři, máme problém – k těmto
souborům se už s původní cestou nedostaneme a museli bychom složitě
modifikovat to, co nám vrátil find. Co ale kdybychom nejdříve zpracovali
celý obsah adresáře a samotný adresář přejmenovali až na konci? A přesně k tomu
slouží přepínač -depth.
Celý zkonstruovaný příkaz pak vypadá takto:
find . -depth -name "*.tvuj" -exec \
sh -c 'mv "$0" "${0%.tvuj}.muj"' "{}" \;
Jiná verze používající nezmíněný, ale šikovný příkaz rename:
find . -depth -name "*.tvuj" -exec \
rename "s/tvuj$/muj/" "{}" \;
Úkol 4 – Paralelizace
Při vymýšlení řešení jste mohli narazit na několik záludností. Aby bylo možné
v bashovském skriptu odchytávat signál SIGCHLD, je potřeba zapnout job control
pomocí set -m. Stále však můžeme narazit na to, že se stejné signály
neřadí do fronty. Pokud skončí dva paralelní úkoly současně, může se stát, že
zaznamenáme jen jeden signál.
Mohli bychom to obejít tím, že každý z řádků obalíme naší vlastní funkcí. Ta nás bude o dokončení informovat nějakým jiným způsobem – například zápisem řádku do jednoho společného souboru.
Také si musíme dát pozor na další zákeřnost. Není úplně dobré číst jeden vstup ve více paralelně běžících vláknech. Nikdo nám totiž nezaručí, že se data rozdělí přesně po celých řádcích.
Zkusíme se tedy těmto úskalím vyhnout:
max="$1"
while read cmd; do
cnt="`jobs | wc -l`"
if [ "$cnt" -ge "$max" ]; then
wait -n
fi
eval "$cmd" &
done
wait
Vždy ve smyčce překontrolujeme počet běžících jobů – řádků vstupu. Pokud jich
je méně než maximum, spustíme další. Jinak pomocí wait -n počkáme na
konec libovolného z nich. V některých shellech tento parametr chybí. Pro ně můžeme
kontrolu nahradit aktivní smyčkou.
Pozor na to, že `jobs | wc -l` může běžet v subshellu, ze kterého již
nebudou vidět naše spouštěné příkazy. V některých shellech je potřeba místo
tohoto řádku používat přesměrování do souboru. Výsledek by pak vypadal následovně:
max="$1"
tmp="`mktemp`"
trap "rm -f "$tmp";echo;exit 0" INT QUIT
while read cmd; do
jobs > "$tmp"
cnt="`wc -l < "$tmp"`"
while [ "$cnt" -ge "$max" ]; do
sleep 1
jobs > "$tmp"
cnt="`wc -l < "$tmp"`"
done
eval "$cmd" &
done
wait
rm -f "$tmp"
Vaší pozornosti doporučujeme ještě použitý příkaz mktemp pro vytvoření
dočasných souborů. Ten vytvoří soubor (případně adresář -d) s unikátním
názvem. Už nikdy si tak pomocnými soubory nepřepíšete důležitá data, případně
nezanesete svůj pracovní adresář či home.
Pro zajímavost si ještě ukážeme, že paralelizace můžeme dosáhnout i využitím
make. Zavoláme-li jej s parametrem -j [N], bude se provádět vždy
nejvýše N cílů současně. Make přitom dodrží všechny závislosti. Čtvrtý úkol
tedy šlo vyřešit i následovně:
mf=`mktemp`
cat -n | sed -r > "$mf" \
's/[[:space:]]*([0-9]+)\t(.*)/pr\1:\n\t\2\n/'
make -sBf "$mf" -j $1 `grep ^pr "$mf" | tr -d :`
rm -f "$mf"
Vstup převedeme na Makefile, kde každému řádku odpovídá jedno pravidlo,
a následně necháme make paralelně provést všechna pravidla. Důležitý je
parametr -B, díky kterému se znovu provede vše nezávisle na existenci
souborů se stejným názvem jako pravidlo. Prakticky tím děláme ze všech cílů
.PHONY. Parametr -s zařídí, aby make nevypisoval právě prováděný příkaz.
Trik s make je pro obecné skripty trochu nepraktický, ale pokud chcete například hromadně vytvářet náhledy fotek, vyjde výroba Makefile a shellového skriptu přibližně nastejno.
Pro úplnost dodejme, že v GNU rozšíření xargs existuje parametr
-P, kterým můžeme paralelizaci snadno získat. Řešení zkrátíme na
xargs -P $1 -n 1 -d "\n" bash -c. Jenom jsme museli omezit počet
parametrů pro jedno spuštění příkazu pomocí -n 1 a vybrat nový řádek
jako jediný oddělovač.
Úkol 5 – Výpis procesů
Zde nebylo skoro co řešit. Jednoduše stačilo v každém adresáři složeném pouze
z čísel (resp. začínajícím na číslo) přečíst pár souborů a hezky je vypsat – s tím nám pomůže starý známý column ze čtvrtého dílu seriálu.
Seznam všech argumentů dostaneme z /proc/PID/cmdline. Jenom jsou oddělené
pomocí nulového bytu, který v terminálu není vidět. Můžeme ho snadno zobrazit
pomocí tr "\0" " ", nebo xargs -0 echo. Protože echo je
defaultní příkaz pro xargs, nemusíme jej ani psát.
{ echo "PID#User# RSS#CWD#Command"
for i in /proc/[0-9]*; do
cd "$i" || continue
pid="${i#/proc/}"
uid="`grep ^Uid: status | cut -f 3`"
unm="`getent passwd "$uid" | cut -f1 -d:`"
rss="`grep ^VmRSS: status | cut -f 2`"
cwd="`readlink cwd`"
cmd="`xargs -0 < cmdline`"
[ -z "$unm" ] && unm="$uid"
[ -z "$rss" ] && rss=" ?"
[ -z "$cwd" ] && cwd="?"
[ -z "$cmd" ] && cmd="?"
[ -e ./ ] || continue
echo "$pid#$unm#$rss#$cwd#$cmd"
done } 2>/dev/null | sort -n | column -s "#" -t
Protože náš skript chvíli poběží, mohou mezitím některé procesy skončit. Kdybychom měli opravdu velkou smůlu, vznikne v průběhu jiný proces se stejným PID. Pak by se mohlo stát, že na jednom řádku budeme mít kombinaci informací o dvou procesech.
Popsanému problému jsme se však vyhli tím, že měníme náš pracovní adresář.
Pokud vznikne nový proces se stejným PID, vznikne také nový adresář se stejným
jménem. Ten starý, ve kterém jsme, již existovat nebude. Pokud tedy proces
skončí dřív, než o něm zjistíme veškeré informace, raději je nevypíšeme vůbec.
O to se postará [ -e ./ ] || continue.
Úkol 6 – Jednoduchý Makefile
Toto bylo v podstatě cvičení na to, jestli jste pochopili smysl Makefilů. Pro většinu z vás to nebylo nic těžkého, Makefile odpovídající zadání by mohl vypadat třeba takto:
A: A.data
B: B.data
C: C.data
AB: A.data B.data
BC: B.data C.data
%:
generuj $^ >$@
FIN1: A AB B
FIN2: BC C
FINAL: A AB B BC C
FIN%:
finalizuj $^ >$@
Abychom nemuseli příkaz psát ke každému cíli, tak jsme pro každý cíl
specifikovali jen jeho závislosti a příkazy jsme napsali vždy pro celou skupinu
cílů najednou. Jak jste si mohli ozkoušet, make volí vždy ten nejvíce
specifický cíl, takže bylo možné příkaz generuj umístit do obecného cíle
% a příkaz finalizuj do (o trochu méně) obecného cíle FIN%.
Závislosti u finálních souborů byly natolik specifické, že je bylo nutné vypsat
ručně, ale nešla by nějak zautomatizovat tvorba základních souborů? Šla
a Richard Hladík přišel s velmi elegantním postupem. Dá se využít prostá
shellová expanze wildcardů, kdy se [AB].data expanduje na
A.data B.data (pokud tyto existují, což jsme ale měli slíbeno).
Tímto velmi elegantním způsobem šlo místo pěti pravidel pro výrobu
„písmenkových“ souborů a jednoho společného pravidla použít jen upravené
společné pravidlo a přídavné pravidlo, že %.data na ničem nezávisí.
Zkrácená verze tedy vypadá takto:
%.data:
FIN1: A AB B
FIN2: BC C
FINAL: A AB B BC C
%: [%].data
generuj $^ >$@
FIN%:
finalizuj $^ >$@
Teď ke generování:
-
make FINAL: Dojde k vyrobení všech „písmenkových“ souborů a souboruFINAL. -
make FIN1: Protože už jsou souboryA,ABiBvygenerované, vyrobí se jen souborFIN1. -
touch A.data -
make FIN2: Na souborech, na kterých závisí tento cíl (BCaCa tranzitivněB.dataaC.data) se nic nezměnilo, a tak se vyrobí jen souborFIN2. -
touch C.data -
make FIN1: Protože se od doby vygenerováníFIN1změnil souborA.data, musí se znovu vygenerovat souboryA,ABa teprve po nichFIN1.
Úkol 7 – Cyklický Makefile
Poslední úkol se možná ukázal trošku složitějším na správné pochopení zadání, ale když se na něj člověk chvíli díval (a třeba si závislosti nakreslil na papír), tak byl řešitelný celkem jednoduše.
Pokud si napíšeme Makefile jako tento níže (a když víme, že při zavolání
příkazu pdftex nám vznikne i nový obsah.toc), tak už je problém
vidět. Každé zavolání make kniha.pdf nám způsobí přegenerování všeho,
i když se zdroják vůbec neměnil.
kniha.tex: zdrojak.tex obsah.toc
cat $^ >$@
kniha.pdf: kniha.tex
pdftex $<
Řešením je používat pomocný soubor s obsahem, a jen pokud se ten změní, přenést změny i do hlavního souboru s obsahem (a tím změnit jeho čas modifikace). Třeba takto:
obsah2.toc: obsah.toc
diff $< $@ || cp $< $@
kniha.tex: zdrojak.tex obsah2.toc
cat $^ >$@
kniha.pdf: kniha.tex
pdftex $<
Pravidlo obsah2.toc přepíše tento soubor, pouze pokud se liší od souboru
obsah.toc. Při opakovaném spuštění make kniha.pdf se tedy jen
porovnají změny (pokud nejsou, opakovaný překlad TeXu se neprovede).