Třetí série dvacátého osmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 28-3-1: Pyramida z helmic
- 28-3-2: Líný písař
- 28-3-3: Formulář na zbroj
- 28-3-4: Katapulty
- 28-3-5: Závaží z fošen
- 28-3-6: Počítání přeživších
- 28-3-7: Legie v lese
- 28-3-8: Inteligence hejna
 28-3-1 Pyramida z helmic (Zadání)
28-3-1 Pyramida z helmic (Zadání)
 Úvodem dnešních řešení se vám všem musíme omluvit za naprosto neodpovídající
ohodnocení pyramidové úlohy (a to ještě vypadalo krásně, že nejlehčí úloha
vyšla jako první!). Pokud jste si tedy nad úlohou lámali hlavu a nemohli na
nic kloudného přijít, možná jste jen projevili víc rozumu než orgové, kteří
kdysi uvěřili tomu, že úloha je přece jednoduchoučká.
Úvodem dnešních řešení se vám všem musíme omluvit za naprosto neodpovídající
ohodnocení pyramidové úlohy (a to ještě vypadalo krásně, že nejlehčí úloha
vyšla jako první!). Pokud jste si tedy nad úlohou lámali hlavu a nemohli na
nic kloudného přijít, možná jste jen projevili víc rozumu než orgové, kteří
kdysi uvěřili tomu, že úloha je přece jednoduchoučká.
Doufáme, že příště bude bodové ohodnocení lépe vypovídat o obtížnosti úlohy, a hlavně že jsme nikoho od řešení neodradili. Ale teď už honem na řešení.
Snadno si můžeme rozmyslet, že pro N ≤ 2 vždy vyhraje druhý hráč. Naopak dost komplikovaně můžeme dojít k tomu, že pro N ≥ 3 existuje vyhrávající strategie pro prvního hráče.
Nejprve tuto vyhrávající strategii popíšeme, a pak teprve dokážeme, že opravdu funguje a soupeř nemá šanci. Zaveďme si teď pár označení, ať se nám strategie popisuje snáz. Předně, lichým řádkem budeme myslet řádek obsahující lichý počet helmic. Drahý střed pak bude prostřední helmice na nejspodnějším lichém řádku a levný střed prostřední helmice na druhém lichém řádku odspodu. Také si dovolme používat pojem pyramida, přestože tvar, který budou helmice v průběhu hry vytvářet, nebude vždy pyramidu připomínat.
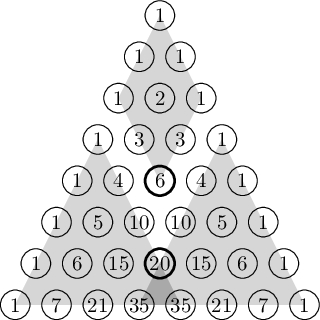
- Hned v prvním tahu shodíme levný střed. Tím jakoby vznikly dvě shodné pyramidy, které se částečně překrývají.
- Potom budeme „kopírovat“ soupeřovy tahy, dokud soupeř nestrčí do drahého středu. Jinými slovy, soupeř strčí do nějaké helmice v jedné z pyramid, my strčíme do stejné helmice ve druhé pyramidě.
- Když soupeř strčí do drahého středu, začneme hrát hladově. To znamená, že vždy shodíme tu helmici, která právě obsahuje nejméně kamínků.
Dokazování vezměme trochu na přeskáčku. Začněme tím, že opravdu můžeme hrát podle druhého bodu. Pyramidy vzniklé po našem prvním tahu totiž mají průnik (překryv) a nemusí být jasné, že pokud soupeř strčí do něčeho z tohoto průniku, můžeme kopírovat.
Ten průnik ale není velký: obsahuje drahý střed a případně (je-li N sudé) dvě helmice pod ním. Drahý střed máme ošetřený zvlášť. Helmice nikdy neshodí helmici stojící vedle ní, takže shodí-li soupeř jednu, my shodíme druhou. Kopírovat tedy můžeme vždy.
To, že každý tah kromě strčení do drahého středu umíme zkopírovat, je důležité. Právě proto to musí být soupeř, kdo strčí do drahého středu, případně ho shodí spolu s helmicí pod ním.
Jak se kopírovací část strategie projeví na počtu sebraných kamínků? Určitě platí, že když okopírujeme tah, sebereme maximálně tolik, kolik sebral soupeř. Ve skutečnosti sebereme ostře méně právě tehdy, když soupeř shodí něco z průniku pyramid. V takovém případě ale určitě shodil drahý střed. To dohromady znamená, že po konci kopírovací strategie se rozdíl našich a soupeřových kamínků zvýší alespoň o hodnotu drahého středu.
Nesmíme ale zapomínat, že před kopírovací částí jsme sami sebrali levný střed. My ovšem ukážeme, že součet kamínků v helmicích, které shodíme shozením levného středu, je o jedna menší než hodnota drahého středu. Když tohle platí, máme po kopírovací strategii alespoň o jeden kamínek méně než soupeř.
Indukcí podle r budeme dokazovat obecnější tvrzení: Počet kamínků získaných shozením střední helmice v r-tém lichém řádku shora je o jedna menší než počet kamínků ve střední helmici na (r+1)-ním lichém řádku.
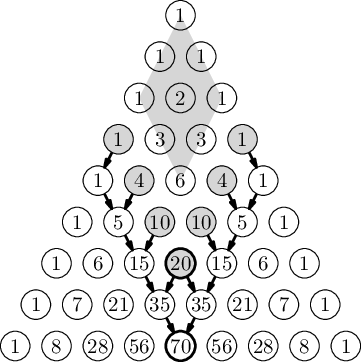
Pro r=1 naše tvrzení evidentně platí (1=2-1). Indukční krok sledujme na obrázku. Pokud shodíme střed 3. lichého řádku, což je číslo 6, spadne celý „diamant“ a z indukce už víme, že jeho součet je 19.
Shodíme-li střed o řádek níž, tedy číslo 20, spadnou navíc dvě diagonály vedoucí od okraje ke středu 20. Šipky na obrázku ukazují, že každá z těchto diagonál se sečte na 35, takže obě diagonály dohromady na 70, což je přesně střed následujícího lichého řádku.
Ovšem číslo 20 leží v obou diagonálách, takže jsme ho započítali dvakrát. To je ale správně: jednou reprezentuje samo sebe, podruhé součet diamantu nad diagonálami zvětšený o jedničku. Analogická úvaha funguje pro libovolné r.
Hurá! Tím jsme ukázali, že po kopírovací části bude mít soupeř alespoň o jeden kamínek víc. Pokud ale soupeř shodí drahý střed přímo, pokračujeme třetí částí (hladovou). Teď musíme ukázat, že i z téhle části získáme nejvýše tolik, kolik soupeř.
Máme před sebou dvě symetrické pyramidy (které už možná jako pyramidy vůbec nevypadají) a chceme získat maximálně stejně, to by svádělo právě k nějaké kopírovací strategii. Jenže my začínáme a nemáme ani tu nejmenší jistotu, že soupeř bude naše tahy kopírovat. Co víc, nemáme ani jistotu, že soupeř bude hrát poslední.
Budeme tedy muset na důkaz toho, že naše strategie funguje, jít jinak. Držte si klobouky, pojedeme z kopce.
 Nejprve si zavedeme další označení, tentokrát pro helmice, na kterých neleží
žádná další (takže jejich shozením neshodíme nic dalšího). Těm budeme říkat
volné.
Nejprve si zavedeme další označení, tentokrát pro helmice, na kterých neleží
žádná další (takže jejich shozením neshodíme nic dalšího). Těm budeme říkat
volné.
Všimněme si, že mezi všemi helmicemi s momentálně minimální hodnotou je alespoň jedna volná. To plyne z toho, že směrem dolů hodnoty helmic neklesají. Také si snadno rozmyslíme, že my bereme vždy volnou helmici – alespoň nějaká z nich má nejmenší hodnotu, takže se nám určitě nevyplatí shazovat helmic víc.
Přiřaďme teď jednotlivým helmicím v jedné ze symetrických pyramid označení xi taková, že xi ≤ xi+1. Každé xi se ve hře (resp. této hladové části hry) vyskytuje dvakrát – na začátku je jednou v první pyramidě, jednou ve druhé.
Helmice můžeme rozdělit na naše a na soupeřovy podle toho, kdo je shodil. K tomu si zavedeme další označení, a to hlavní helmice. To bude pro každý tah nejmenší z helmic, které hráč v daném tahu shodil. Pokud helmic shodil více, označíme ty ostatní jako vedlejší.
Snadno si všimneme, že všechny naše helmice jsou hlavní (jelikož nikdy neshodíme víc než jednu helmici naráz).
Nyní bychom chtěli spárovat své helmice se soupeřovými, a to tak, aby vždy naše helmice měla maximálně takovou hodnotu, jakou má spárovaná soupeřova helmice. Některé soupeřovy helmice možná zůstanou nespárované, ale to nám nijak nevadí. Kdyby se nám takové párování podařilo najít, musí být náš počet kamínků maximálně stejný jako soupeřův.
Představme si, že vždy spárujeme naši hlavní helmici s hlavní helmicí, kterou soupeř vezme v příštím tahu. Pro takové párování by nerovnost určitě platila. Jenže se může stát, že v posledním tahu hrajeme my, tedy zbývá jedna nespárovaná helmice, kterou už není s čím spárovat. Ukážeme ale, že v takovém případě můžeme helmice přepárovat.
Označme nespárovanou helmici jako X a její hodnotu jako xi. Nyní se podíváme na suffix xi, … , xN všech hodnot, které byly ve hře. Existují dvě možnosti.
Zaprvé, existuje vedlejší soupeřova helmice s hodnotou z tohoto suffixu. Jelikož jsme zatím párovali vždy s hlavními helmicemi, je tato vedlejší helmice nespárovaná, a navíc má určitě aspoň stejnou hodnotu jako X. Tedy můžeme X spárovat s touto vedlejší helmicí. Tím máme vše spárováno a nerovnosti platí.
Zadruhé, žádná taková vedlejší helmice neexistuje. To znamená, že suffixu odpovídají pouze hodnoty hlavních helmic. Zároveň ovšem suffixu odpovídají hodnoty sudého počtu helmic, a jedna z těchto helmic je X. To znamená, že alespoň jedna hlavní helmice je spárovaná s nějakou, jejíž hodnota je menší než xi.
Označme helmice v tomto páru jako A a B, nechť A ≤ B (tedy hodnota A v suffixu neleží, hodnota B ano). V dosavadním párování platí, že hodnota naší helmice je menší než soupeřovy, tedy A je naše. Přepárujme nyní X s B; A se stane nespárovanou.
Jelikož xi bylo v suffixu nejlevěji, je určitě hodnota X neostře menší než hodnota B, takže nerovnosti nám stále platí. Může se zdát, že jsme si nepomohli, opět máme jednu nespárovanou helmici. Její hodnota ale určitě leží v řadě hodnot o jedna víc než vlevo, tedy opakováním přepárování spárujeme všechny helmice v konečném čase.
Tady ještě zdůrazněme, že pokud se dostaneme až do situace, kdy má nespárovaná helmice hodnotu x1, musí mít soupeř nutně alespoň jednu vedlejší helmici. V opačném případě by muselo existovat párování vedoucí před suffix, ale před x1 už nic není.
Vždy tedy umíme vytvořit párování takové, že naše helmice má maximálně stejnou hodnotu, jakou soupeřova, tedy i z hladové části hry budeme mít maximálně tolik, kolik získá soupeř.
Tím jsme dokázali, že popsaná strategie je skutečně vyhrávající. Ufff!
 28-3-2 Líný písař (Zadání)
28-3-2 Líný písař (Zadání)
Označme si věty jako řetězce A a B, bez újmy na obecnosti předpokládejme, že |A| ≥ |B|. Podívejme se nejprve, jakým způsobem sestrojíme řetězec S takový, aby obsahoval po odstranění některých znaků každou větu a také byl nejkratší, neboli aby tento řetězec byl nejkratší společnou nadposloupností A, B. Jak ale tento řetězec bude vypadat?
Určitě se nám vůbec nevyplatí mít délku |S| > |A|+|B|, jelikož bychom museli přidat další zbytečné znaky. Řetězec dále můžeme zkrátit tím, že znaky společné oběma větám zapíšeme do našeho řetězce S jen jednou.
Tyto společné znaky však vůbec nemusí být na stejných pozicích u obou řetězců. Příkladem jsou řetězce
xAxBxCxDxE, B=klmABCDkElm,
kde společné znaky ABCDE tvoří nejdelší společnou podposloupnost
(zkráceně NSP). Znaky této NSP se ale v obou řetězcích vyskytují na
různých indexech: v A na indexech [1,3,5,7,9] a v B na indexech
[3,4,5,6,8]. My potřebujeme zjistit jak samotnou NSP, tak indexy
jejích znaků v obou řetězcích.
K vyřešení problému nalezení NSP lze využít dynamického programování, algoritmus je přímo popsán v kuchařce. Tento algoritmus nás stojí O(|A|·|B|) času.
Jakmile máme indexy společných znaků z obou vět, můžeme sestrojit náš požadovaný řetězec S. Mějme i-tý společný znak, ai a bi indexy tohoto společného znaku v A a B. Potom postupně budeme zvyšovat i od 1 po délku NSP a při každé iteraci vypíšeme všechny znaky z A, B mezi (i-1)-ním a i-tým společným znakem a nakonec samotný i-tý znak. Tento algoritmus nám zabere O(|A|+|B|) času.
Celkově algoritmus zabere O(|A|·|B|) času. Důvod je takový, že nám právě nejvíce času potrvá vyhledání NSP. Samotné vypsání řetězce trvá jen lineárně, což nám asymptotickou složitost nezmění.
Jiný pohled na úlohu
Na tuto úlohu existuje i řešení založené na odlišné myšlence, které nakonec bude stejně efektivní. Představme si orientovaný graf, jehož vrcholy jsou reprezentovány uspořádanou dvojicí [ai,bi]. Tyto vrcholy si můžeme graficky znázornit, že jsou položené na mřížce o velikosti |A|, |B|, ve které souřadnice vrcholů určují indexy jednotlivých řetězců s tím, že vlevo nahoře máme vrchol S = [0,0] a vpravo dole je vrchol C = [an-1,bn-1].
Pro každý vrchol dále bude platit, že z něj vede hrana doprava a dolů vždy, pokud není poslední ve své souřadnici, a dále si zavedeme zkratkové hrany, které nám budou vést přes diagonálu dolů doprava. Tyto hrany budou vést z těch vrcholů, které nám označují znak společný oběma řetězcům.
Nyní, když máme takový graf postavený, nalezneme nejkratší cestu z vrcholu [0,0] do vrcholu [A,B]. Jakmile jsme jednu takovou cestu našli, vydáme se po ní a zařídíme se podle toho, kterým směrem se rozhodneme vydat z vrcholu [ai,bj]:
- Pokud je následující vrchol cesty napravo od aktuálního, vypíšeme na výstup znak ai.
- Pokud je následující vrchol cesty směrem dolů od aktuálního, vypíšeme znak bi.
- Pokud se následující vrchol cesty nachází směrem po diagonále, je celkem jedno, který znak necháme vypsat, protože aktuální vrchol označuje společný znak.
Tímto jsme vypsali na výstup hledanou nejkratší společnou nadposloupnost. Samotné sestavení grafu nám potrvá O(|A|·|B|), jelikož tento graf má počet vrcholů stejný, jako je součin délky obou řetězců A ·B. Nejkratší cestu potom umíme nalézt v lineárním čase jednoduchým prohledáním, takže nám to časovou složitost neporuší. Výsledný algoritmus má tímto stejnou asymptotickou složitost jako algoritmus popsaný výše.
 28-3-3 Formulář na zbroj (Zadání)
28-3-3 Formulář na zbroj (Zadání)
Nejprve si úlohu převedeme na grafovou. Pro každý formulář vytvoříme jeden vrchol. Říkejme, že formulář x (přímo) závisí na formuláři y, pokud k získání x musíme předložit vyplněné y. Pro každou takovouto dvojici vytvoříme v grafu orientovanou hranu x →y. Některé formuláře jsou vydávány „zadarmo“ (nemají závislosti). Odpovídající vrcholy v grafu nemají žádné výstupní hrany – takovéto vrcholy obvykle nazýváme stoky.
Graf závislostí může vypadat třeba takto:
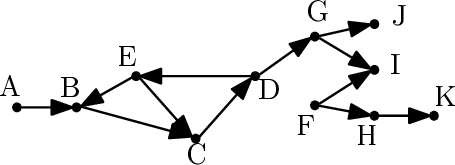
Stoky jsou v tomto případě vrcholy I, J, K. Dále řekneme, že nějaký formulář x nepřímo závisí na y, pokud z x vede orientovaná cesta do y. Takový x nemůžeme získat, aniž bychom někdy předtím získali y. Například F nepřímo závisí na K, a vskutku: bez K nedostaneme H, a tedy ani F.
Pokud nějaký formulář leží na orientovaném cyklu, nepřímo závisí sám na sobě. Takový určitě nemůžeme získat: například abychom získali E, potřebujeme C, který vyžaduje D, a ten zase E. Jinými slovy abychom dostali E, museli bychom nejdřív mít E. To určitě nejde, protože úředníci nevydávají formuláře na dluh.
Dalším formulářem, který určitě nemůžeme získat, je A, protože závisí na B, který leží na cyklu.
Řešení prohledáváním do hloubky
Pro každý formulář budeme chtít určit jeho ohodnocení, které může nabývat jedné ze tří následujících hodnot:
- 0, pokud formulář lze získat vyplněný záporně
- 1, pokud formulář lze získat vyplněný kladně
- X, pokud formulář není možné získat
Ohodnocení formuláře x najdeme jednoduchou rekurzivní funkcí Ohodnoť(x). Ta nejprve rekurzivním zavoláním získá ohodnocení všech přímých závislostí x, na jejich základě určí ohodnocení x, a to vrátí. To vlastně není nic jiného než prohledávání do hloubky.
Protože funkce Ohodnoť může být na tentýž formulář zavolána mnohokrát a nechceme plýtvat časem opakováním toho samého výpočtu, použijeme dynamické programování. Již spočítaná ohodnocení si budeme ukládat do pole H indexovaného čísly formulářů. Pokud je při zavolání Ohodnoť(x) hodnota H[x] již známa, prostě ji rovnou vrátíme a nepočítáme znovu.
Kostra ohodnocovací logiky je jednoduchá: pokud některou ze závislostí x nejde získat (má ohodnocení X), ani x nemůžeme získat, tedy vrátíme rovněž X. Pokud naopak jde získat všechny, pak jde získat i x a jeho ohodnocení vytvoříme tak, že ohodnocení závislostí zkombinujeme předepsanou logickou funkcí.
Ale to nestačí. Pokud graf obsahuje cykly, takováto implementace by skončila nekonečnou rekurzí. Potřebujeme umět nějak cykly detekovat a vrcholy na nich označit jako nezískatelné.
To můžeme udělat například tak, že na začátku funkce Ohodnoť(x) si vrchol x označíme jako rozpracovaný (a na konci toto označení zase zrušíme). Pokud potom někdy při procházení závislostí narazíme na rozpracovaný vrchol, víme, že leží na cyklu. Proč? Pokud narazíme při prohledávání na rozpracovaný vrchol x, znamená to, že funkce Ohodnoť(x) aktuálně běží (v nějakém vyšším patře rekurze). Všechny vrcholy, které navštívíme, zatímco běží Ohodnoť(x), patří mezi (nepřímé) závislosti x. Takže pokud narazíme na x, znamená to, že x závisí na x.
Zavedeme si dvě pomocné hodnoty, které se mohou vyskytovat v poli H, pokud ohodnocení daného vrcholu ještě neznáme:
- ?, pokud jsme dané pole ještě nenavštívili
- R, pokud je vrchol právě rozpracovaný
Upravený algoritmus bude vypadat následovně:
Ohodnoť(x):
- Pokud H[x] = R:
- H[x] ←X, vrať X.
- Pokud H[x] ≠ ?: vrať H[x].
- H[x] ←R
- Označ z1 až zk všechny závislosti x.
- Pro i=1 až k:
- h ← Ohodnoť(zi)
- Pokud h=X:
- H[x] ←X, vrať X.
- H[x] ←f(H[z1],… ,H[zk]), přičemž f je logická funkce předepsaná pro formulář x (and, or nebo xor).
- Vrať H[x].
Protože chceme zjistit ohodnocení všech formulářů, prostě funkci Ohodnoť zavoláme postupně na všechny vrcholy. Celkem budeme potřebovat lineární čas, přesněji O(N+M), kde N je počet formulářů a M je celkový počet závislostí. To nahlédneme následovně. Vnitřní část funkce Ohodnoť provedeme pro každý vrchol nejvýše jednou. Tím pádem nejvýše jednou provedeme vnitřní cyklus přes všechny hrany vycházející z daného vrcholu. Tudíž na každou hranu se podíváme maximálně jednou.
Ještě musíme uvážit čas strávený na prvních třech řádcích funkce Ohodnoť, které mohou být provedeny víckrát. Ale funkce Ohodnoť je volána jen ze dvou míst:
- Z hlavní smyčky, kde je volána jednou pro každý vrchol (celkem N×).
- Rekurzivně z jiného volání Ohodnoť, ale to se děje právě v místě, kde procházíme výstupní hrany. A už víme, že každou hranu navštívíme maximálně jednou, tedy těchto volání funkce Ohodnoť je dohromady maximálně M.
Z tohoto odhadu je taky vidět, že teď už se náš algoritmus nemůže zacyklit.
 28-3-4 Katapulty (Zadání)
28-3-4 Katapulty (Zadání)
Podívejme se prvně na lehčí variantu. Nabízí se umisťovat katapulty hladově, tedy dát každý katapult co nejlevěji to půjde.
Řekněme, že projdeme bitevní lajnu zleva a při procházení si udržujeme množinu dosud neumístěných katapultů, které můžeme umístit na aktuální políčko.
Na každém políčku pak přidáme do množiny katapulty, které můžeme nově umístit, a poté z téhle množiny vezmeme katapult, jehož úsek končí nejdříve. Zkontrolujeme, že pravá hranice povoleného úseku je maximálně rovna aktuální pozici, a pokud ano, katapult umístíme na toto políčko. Pokud náhodou ne, zahlásíme, že řešení neexistuje. Budeme-li mít zrovna prázdnou množinu, jednoduše se posuneme na další políčko.
Snadno nahlédneme, že pokud náš algoritmus vydá řešení, bude toto řešení korektní – každý katapult bude ve svém úseku a zároveň bude na každém políčku jen jeden.
Musíme ale také ukázat, že pokud naopak ohlásíme neexistenci řešení, skutečně žádné řešení neexistuje. Když jsme vyhlásili neúspěch, máme nějaký katapult P, který jsme nedokázali umístit. Na každém políčku v úseku, kam smíme P umístit, už se ale vyskytuje jiný katapult, jehož úsek končí nejpozději stejně, tedy žádný z nich nemůžeme přesunout doprava.
Ještě musíme uvážit, jestli jsme některý z těch katapultů nemohli umístit více vlevo. Podobným argumentem ale ukážeme, že ne – když vezmeme největší levou hranici těchto katapultů a podíváme se na úsek mezi ní a začátkem úseku pro P, opět máme na každém políčku katapult, který nemůžeme přesunout doprava.
Takto dojdeme až na začátek lajny. Vlastně to znamená, že se snažíme umístit L+1 katapultů na L políček, a to evidentně jít nemůže. Náš algoritmus tedy ohlásí neúspěch, pouze když řešení neexistuje.
Připomeňme teď, že počet katapultů označujeme K a délku lajny N.
Nejprve si všechny katapulty seřadíme podle levé hranice vzestupně. Tím pádem se můžeme postupně posouvat v poli katapultů a nalezení katapultů, které máme přidat do množiny, trvá lineárně v jejich počtu, za celý algoritmus tedy O(K). Samotné řazení nám zabere O(K log K).
K udržování katapultů, resp. k jejich přidávání a nalezení toho s minimální pravou hranicí, nám dobře poslouží halda. Tak bude každá operace trvat O(log K).
Nejprve tedy seřadíme katapulty a pak projdeme celou bojovou lajnu. Tento průchod nám trvá O(N), na každém políčku se ptáme na katapult s minimální souřadnicí a možná přidáváme katapulty do množiny. Takových přidání je ale dohromady O(K), takže celková časová složitost algoritmu je O(N log K). Přesněji tedy (K log K + N log K), ale klidně předpokládejme K ≤ N. Paměťová složitost je lineární v počtu katapultů, tedy O(K).
Pěkné je si všimnout, že políčka, na kterých se nic neděje, jsou nezajímavá a vlastně nás jen zdržují. Líbilo by se nám umět skákat jen po těch, kde se něco děje. To ale umíme zařídit – o každém katapultu víme, kde jeho úsek začíná a končí, takže se můžeme buď posunout o jedno políčko (máme-li po umístění katapultu neprázdnou množinu), nebo rovnou skočit na příští událost.
Události si můžeme udržovat v haldě, na každém políčku tedy ještě přidáme případné zjištění příští události. Jelikož pro umístění K katapultů použijeme nejvýš K políček, bude celková složitost O(K log K).
Teď těžší varianta, a pozor, přijde trik :) Všimneme si, že souřadnice katapultů jsou nezávislé – bez ohledu na to, do kterého řádku katapult umístíme, můžeme ho umístit do stejných sloupců.
Řešením úlohy tak není nic jiného než dvojí spuštění lehčí varianty, jednou pro řádky, jednou pro sloupce. A jelikož dvojka je konstanta, časová složitost zůstává O(K log K).
 28-3-5 Závaží z fošen (Zadání)
28-3-5 Závaží z fošen (Zadání)
Nejprve fošny ze zadání ohoblujeme až na strohou geometrickou realitu: Dostali jsme n desek, každá má danou šířku a výšku, všechny mají jednotkovou tloušťku. Chceme vytvořit kvádr. Uděláme to tak, že si vybereme podmnožinu desek, položíme je na sebe a případně některé z nich o 90 ° otočíme. Nakonec je ořízneme na šířku nejužší desky a výšku té nejnižší. Chceme přitom, aby vznikl kvádr o největším možném objemu.
Jak se zbavit otáčení
Úloha má nepříjemně mnoho stupňů volnosti: nejen, že si vybíráme, které desky použijeme, ale pro každou ještě určujeme natočení. Pojďme se otáčení zbavit. Dokážeme, že pokud každou desku předem natočíme „naležato“, tedy tak, aby její šířka byla větší nebo rovná výšce, o optimální řešení nepřijdeme.
Nejprve uvažujme situaci se dvěma deskami rozměrů a×b a x×y (první rozměr je šířka, druhý výška). Jistě můžeme předpokládat, že a≥ b a x≥ y (jinak desku otočíme) a navíc b≥ y (první deska je ta vyšší). Aby vznikl kvádr maximálního objemu, chceme desky posunout a otočit tak, aby se překrývaly v co největší ploše. Překryv jistě nezmenšíme, přiložíme-li na sebe levé dolní rohy obou desek.
Nyní rozlišíme dva případy. V prvním je x≤ a, čili nižší deska je i užší (levý obrázek). Tehdy se desky překrývají celou plochou té menší z nich, takže se jistě nevyplatí kteroukoliv desku otáčet.
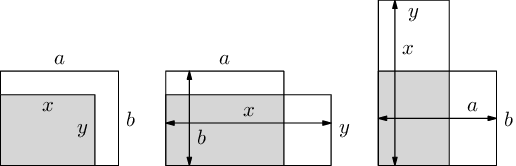
Zbývá nám případ x>a. Pokud obě desky ponecháme orientované stejně (prostřední obrázek), jejich společná část bude mít obsah a·y. Pakliže je vůči sobě otočíme (pravý obrázek), vyjde obsah b·y. První varianta je ovšem stejná nebo lepší, neboť a≥ b.
V obou případech platí, že překrývající se část má opět šířku větší nebo rovnou výšce, takže postup můžeme opakovat a o všech použitých deskách dokázat, že jsme je mohli nechat naležato. Ve zbytku řešení tedy budeme bezelstně předpokládat, že deskami není možné otáčet.
Elementární řešení
Náš první pokus o algoritmus bude založený na jednoduchém pozorování: výsledný kvádr zdědí jak svou šířku, tak svou výšku od některé desky, každou možná od jiné. Stačí tedy vyzkoušet n možných šířek, k nim n možných výšek a pokaždé probrat všechny desky a použít ty, které jsou dostatečně široké a vysoké. To zvládneme v čase O(n3) a získáme za to pár bodů.
Mimochodem, řešení tohoto druhu by fungovalo, i kdybychom brali v úvahu otáčení. Výšku i šířku kvádru bychom vybírali ze všech výšek i šířek (celkem 4n2 možností) a při testování, zda se deska vejde, bychom zkoušeli obě možné orientace.
Chytřejší řešení
V minulém řešení počítáme stále dokola podobné věci, takže zkusíme výpočet přeuspořádat, abychom se tomu vyhnuli.
Nadále budeme zkoušet všech n možných šířek. Pro každou šířku w vybereme všechny dostatečně široké desky. Budeme je procházet od nejvyšší k nejnižší a průběžně přepočítávat aktuální kvádr. Pro nejvyšší desku samotnou má kvádr šířku w, výšku této desky a tloušťku 1. Když přidáme další, nižší desku, šířka zůstane, výška klesne a tloušťka vzroste o 1. Tak pokračujeme a pokaždé spočítáme objem aktuálního kvádru a započítáme ho do průběžného maxima.
Toto vše se dá stihnout v čase O(n2): na počátku výpočtu setřídíme všechny desky podle výšky. Pak zkoušíme (v libovolném pořadí) všech n možných šířek, pro každou z nich probíráme desky v setříděném pořadí, přeskakujeme ty příliš úzké a pro ostatní v konstantním čase přepočítáváme objem kvádru.
Autor přiznává, že stále věří v existenci rychlejšího řešení, ale postupně si všechna taková vyvrátil. Kdybyste o nějakém věděli, dejte nám prosím vědět.
 28-3-6 Počítání přeživších (Zadání)
28-3-6 Počítání přeživších (Zadání)
Aby řešení mohlo existovat, graf musí být souvislý. To budeme nadále předpokládat. Nejprve vyřešíme jednodušší variantu, kdy graf přátelství je stromem. Hledanému předpisu, kdo komu má helmici předat, budeme říkat plán pro daný strom. Ten si lze představit prostě jako posloupnost vrcholů, kde dva sousední jsou vždy vzdálené ve stromě nejvýše tři hrany.
Strom si zakořeníme a použijeme obvyklý trik na stromové úlohy. Nejprve rekurzivně najdeme plán pro každý podstrom kořene a pak tyto plány nějak napojíme, abychom z nich poskládali plán pro celý strom. Předpokládejme pro začátek (později se ukáže, že je to trochu složitější), že každým podstromem začne helmice putovat od kořene.
To znamená, že když helmice opouští první podstrom, musíme ji předat rovnou kořeni druhého podstromu (přes kořen celého stromu to nejde, tam už byla):
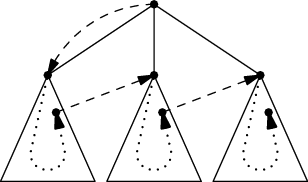
Tečkované čáry značí rekurzivně spočtené plány pro jednotlivé podstromy, čárkované jejich napojení. Aby předání mezi podstromy bylo korektní, musí plán pro každý podstrom končit v prvním patře tohoto podstromu (hned pod jeho kořenem). Kdyby končil hlouběji, předání bude přes víc než tři hrany.
Abychom mohli naše řešení použít rekurzivně, musí tedy i výsledný plán pro celý strom končit v prvním patře. Ale plán nastíněný v obrázku výše zřejmě končí v patře druhém…
Leč není třeba propadat panice. Všimneme si, že kdybychom z kořene poslali helmici do vrcholu, který je aktuálně poslední, a celý průchod průchod podstromy obrátili (díky neorientovanosti hran můžeme), skončíme v kýženém prvním patře:
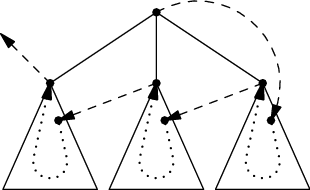
Máme tedy algoritmus, který nalezne plán pro daný strom začínající v kořeni a končící v prvním patře: Rekurzivním zavoláním téhož algoritmu nalezneme plán pro první podstrom kořene a obrátíme v něm pořadí vrcholů (jako první helmici obdrží nějaký vrchol v prvním patře tohoto podstromu, jako poslední jeho kořen). Za tento převrácený plán připojíme rovněž převrácené plány pro druhý, … až poslední podstrom. Helmice tedy skončí v kořeni posledního podstromu, tedy v prvním patře celého stromu, což přesně potřebujeme.
Pro zjednodušení implementace nemusíme plány ani dodatečně obracet. Stačí rekurzivnímu volání navíc předat jeden parametr, zda má generovat normální (z kořene do prvního patra), nebo obrácený (z prvního patra do kořene) plán. Díky tomu si nemusíme plány ukládat, nýbrž můžeme vrcholy rovnou vypisovat.
Snadno si rozmyslíte, že sousední vrcholy plánu jsou vzdálené maximálně tři hrany. Zbývá ještě vyřešit okrajové podmínky rekurze. Zastavíme se na jednovrcholovém stromě (tvořeném listem původního stromu), pro který je plánem prostě jednoprvková posloupnost obsahující tento vrchol.
Celý algoritmus v pseudokódu:
NajdiPlán(u, obrať):
- Pokud obrať=0: vypiš u.
- Pro všechny v syny u:
- NajdiPlán(v, 1-obrať)
- Pokud obrať=1: vypiš u.
Rozmyslete si, že opravdu odpovídá výše popsanému. Výsledný plán může vypadat třeba takto:
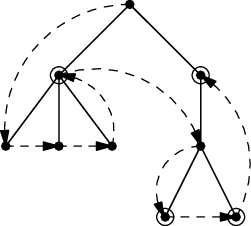
Zakroužkované jsou ty vrcholy, ve kterých hledáme obrácený plán. To jsou právě vrcholy v lichých patrech.
Obecné grafy
Zobecnit řešení na všechny grafy už je jednoduché. Z libovolného grafu můžeme udělat strom tak, že najdeme jeho kostru (např. prohledáním do hloubky) a na ni spustíme výše popsaný algoritmus. Protože pro každý strom existuje řešení, hrany mimo kostru jsou přebytečné a můžeme je ignorovat.
Navíc hledání kostry a konstrukci plánu nemusíme provádět odděleně, nýbrž je můžeme spojit do jednoho DFS průchodu grafem. Podrobněji ve vzorovém programu.
 28-3-7 Legie v lese (Zadání)
28-3-7 Legie v lese (Zadání)
Les je obdélník o hraně L, v němž leží S bodových stromů. Horní stranou do obdélníku vstoupí kruhová legie o průměru D a chce vylézt spodní stranou. Nesmí přitom narazit na žádný strom, ani na levou či pravou stranu obdélníku. Střed legie tedy musí stále udržovat vzdálenost alespoň D/2 od všech stromů i od bočních stran lesa.
Překážky a ploty
Navigační problémy tohoto druhu se řeší snáz, pokud se lesem místo kruhové formace pohybuje jediný bod. Úlohu proto trochu přeformulujeme: každý strom „nafoukneme“ na kruh o poloměru D/2 a boční strany lesa roztáhneme směrem dovnitř na obdélníky široké rovněž D/2. Aby se všechny překážky vešly do lesa, roztáhneme les nahoře i dole o D/2.
Legii naopak smrskneme do jediného bodu. Ten může stát právě na těch místech, která neleží v žádném kruhu ani obdélníku.
Dostaneme tedy nějaké překážky ve tvaru kruhů a obdélníků a ptáme se, zda bod může projít shora dolů a vyhnout se všem překážkám.
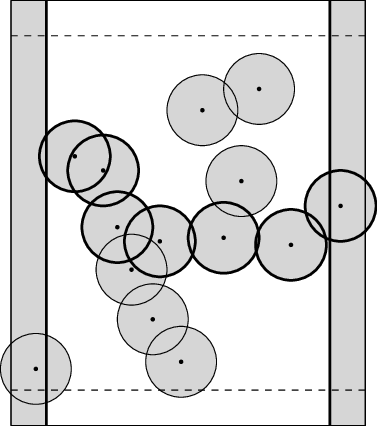
Na předchozím obrázku to možné není, protože v něm existuje plot – posloupnost na sebe navazujících překážek, která spojuje levý okraj s pravým. Každá trasa shora dolů musí plot alespoň na jednom místě protnout, takže trasa narazí na alespoň jednu překážku.
Dokonce platí, že kdykoliv nejde projít shora dolů, existuje nějaký plot, který tomu brání. Vskutku: množina bodů, do kterých se dá shora dojít, tvoří nějakou uzavřenou oblast. Hranice této oblasti se skládá z částí horní, levé a pravé strany lesa a nějakých částí překážek. Představme si, že hranici této oblasti obcházíme od levého horního rohu lesa proti směru hodinových ručiček. Mezi posledním odchodem z levé strany a následujícím příchodem na tu pravou jsme museli projít přes na sebe navazující části překážek. To ovšem znamená, že tyto překážky tvoří plot.
Gigantický graf
Potřebujeme tedy vymyslet, jak hledat plot. Pomůžeme si grafem: jeho vrcholy budou reprezentovat stromy, navíc přidáme vrchol ℓ pro levou stranu lesa a p pro pravou. Hranou spojíme každé dva vrcholy, jejichž vzdálenost v rovině je menší než D. To nastane právě tehdy, když se příslušné překážky protínají. Plot pak odpovídá cestě z vrcholu ℓ do vrcholu p v tomto grafu. Pro příklad z předchozího obrázku vypadá graf následovně:

Stačí tedy zjistit, zda ℓ a p leží v téže komponentě souvislosti. To můžeme otestovat třeba prohledáváním do šířky. Jistou nevýhodou ovšem je, že náš graf může mít až O(S2) hran (rozmyslete si, jak by takový les vypadal). Bude tedy lepší nedržet si celý graf v paměti a vytvářet ho podle potřeby za běhu.
Budeme si udržovat frontu stromů, které máme zpracovat. Na počátku do ní vložíme stromy dosažitelné z ℓ, čili ty, jejichž x-ová souřadnice je menší než D. Pak postupně odebíráme stromy z fronty. Pro každý strom najdeme všechny jeho sousedy, tedy stromy ve vzdálenosti menší než D, a pokud jsme je ještě neviděli, přidáme je do fronty. Skončíme, pokud se fronta vyprázdní, nebo pokud objevíme strom s x-ovou souřadnicí větší než L-D.
To je všechno. Snadné, že? Ale pomalé… Navštívíme až S vrcholů a pro každý z nich procházíme S potenciálních sousedů. Jednoho souseda naštěstí stihneme zpracovat v konstantním čase (místo vzdáleností porovnáváme jejich druhé mocniny, abychom nemuseli odmocňovat), takže celý výpočet trvá O(S2).
Pomohou políčka?
Existuje řada technik, kterými se dá hledání sousedních stromů urychlit. Můžeme například rozdělit les na políčka velikosti D×D a pro každé políčko si předpočítat, jaké stromy v něm leží. Sousedé daného stromu se pak nacházejí buď ve stejném políčku, nebo v některém z osmi okolních.
Tento trik může pro některé kombinace L a D výrazně pomoci. Limity v zadání úlohy bohužel připouštěly i případy, kdy je D řádově stejné jako L. Tehdy je políček konstantní počet, takže okolní políčka obsahují podstatnou část všech stromů. Škoda, tudy cesta nevede.
Znovu zametání
Není náhoda, že jsme k této sérii přibalili geometrickou kuchařku, v níž se ukazuje princip zametání roviny. Hodí se i pro tuto úlohu.
Les budeme zametat zleva doprava svislou přímkou. Budeme si při tom pamatovat, které stromy jsme už potkali. Pokaždé, když zametací přímka narazí na nový strom, najdeme jeho sousedy mezi předchozími stromy a natáhneme do nich hrany. Hledání si urychlíme dvěma triky:
- Nemá smysl zkoušet stromy, které se v y-ové souřadnici liší od nového stromu o více než D.
- Pokud se dva stromy vyskytly v témže řádku, stačí uvažovat pravý z nich. Ten levý je buďto moc daleko, nebo už leží v téže komponentě jako pravý, takže stačí hranu přivést do pravého. (Nezapomeňte, že souřadnice stromů jsou celočíselné, a proto je možných řádků málo.)
Pořídíme si tedy pole indexované číslem řádku (0… L-1). V něm si budeme pro každý řádek pamatovat, jaký nejpravější strom jsme tam viděli. Objeví-li se nový strom v y-tém řádku, stačí se podívat na nejpravější stromy v řádcích y-D až y+D a pro každý z nich zkontrolovat, jak je daleko.
Sousedy jednoho vrcholu tedy projdeme v čase O(D). Celý algoritmus nejprve stráví čas O(S log S) setříděním všech stromů a O(L) inicializací pomocného pole. Poté prochází S stromů a nad každým z nich stráví čas O(D). Tím vytvoří graf o nejvýše O(SD) hranách, který pak prohledá do šířky v čase O(SD).
Celková časová složitost je tedy O(S log S + L + SD).
Implementační (in)triky
Náš ukázkový program se drží předchozího nápadu, ale pro jednoduchost se v některých detailech odchyluje.
Především si místo třídění stromů podle souřadnic vytvoří matici L×L, která o jednotlivých bodech lesa říká, zda tam leží strom. Zametání lesa pak prostě prochází tuto matici po sloupcích a hledá jedničky. Místo O(S log S) tedy potřebuje čas O(L2). To pro limity ze zadání je spíše lepší.
Také místo toho, abychom graf udržovali v paměti a pak ho celý prohledali, udržujeme komponenty souvislosti průběžně v datové struktuře Union-Find. Pro každou z O(SD) hran tedy voláme Union, který trvá O(log S). Kdybychom byli pilnější, použili jsme rychlejší Union-Find se složitostí O(log * S) (Funkce log * x říká, kolikrát musíme číslo x opakovaně zlogaritmovat, než se poprvé dostaneme pod 1. Roste tedy velice pomalu. Funkci α(x) zde definovat nebudeme, ale prozradíme, že roste ještě mnohem pomaleji.) nebo O(α(S)), který je popsaný v kuchařce o minimálních kostrách.
I s jednoduchým Union-Findem má náš program složitost O(L2 + SD log S), což je pro slíbené velikosti vstupu naprosto postačující.
Divotvorný diagram
Zbývá hrstka pochybností, zda by úlohu šlo řešit efektivněji, zejména v případě, kdy by nám nikdo neslíbil celočíselné souřadnice. Pochybnosti samozřejmě nejsou na místě, známe řešení v čase O(S log S) s použitím jednoho milého králíka z kouzelnického klobouku výpočetních geometrů. Jen je to trochu pracnější, takže vše pouze načrtneme. Detaily můžete najít v geometrické kapitole medvědí knížky.
 Nechť S je množina stromů v rovině. Pro každý strom s∈S
definujeme jeho oblast Rs jako množinu všech bodů roviny,
pro něž je s nejbližší strom (respektive jeden z nejbližších stromů,
pokud jich je víc).
Nechť S je množina stromů v rovině. Pro každý strom s∈S
definujeme jeho oblast Rs jako množinu všech bodů roviny,
pro něž je s nejbližší strom (respektive jeden z nejbližších stromů,
pokud jich je víc).
Podívejme se na nějaké dva stromy x a y. Všechny body roviny, které mají k x blíže než k y, tvoří polorovinu (hraniční přímkou této poloroviny je osa úsečky xy). Proto musí každá oblast Rs být průnikem konečně mnoha polorovin. Oblasti tedy mají tvar konvexních mnohoúhelníků, případně na jedné straně otevřených do nekonečna.
Vyzkoušíme si to na tomto lese:
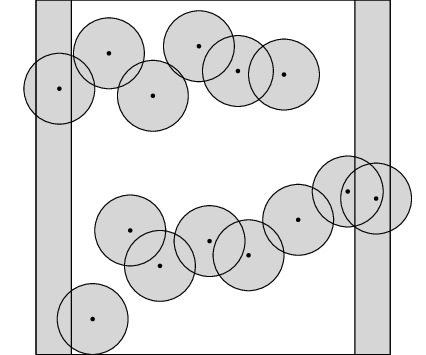
Diagram pro něj vyjde následovně. (Plné i čárkované čáry jsou hranice oblastí, brzy uvidíme, v čem se liší. Obrázek jsme ořízli okrajem lesa.)

Rozkladu roviny na tyto oblasti se říká Voroného diagram (zkoumal ho začátkem 20. století ruský matematik Georgij Voronoj). Je dobré vědět, že je to rovinný graf (až na neomezené stěny, ale to je detail), tudíž pro S stromů má O(S) vrcholů a O(S) hran. Také se hodí znát algoritmus pro jeho konstrukci v čase O(S log S), jako obvykle mazaným zametením roviny – detaily viz medvědí knížka.
Na chvíli zapomeňme, že les má nějaké okraje. Pak platí, že může-li lesem projít kruhová legie, pak jím může projít po hranách Voroného diagramu. Není divu: každá hrana diagramu je osa úsečky mezi dvěma stromy (nebo její část), takže jdeme-li po hraně, dodržujeme maximální možnou vzdálenost od této dvojice stromů.
Stačilo by tedy sestrojit diagram, pro každou hranu spočítat vzdálenost stromů, které tato hrana odděluje, a pokud je to méně než D, hranu smazat (na obrázku jsou tyto hrany čárkované). Tím by vznikl nějaký lineárně velký graf, který bychom vzápětí prohledali do šířky. To dává hezké řešení v čase O(S log S).
Jenže teď si na okraje zase musíme vzpomenout. Co to způsobí? Část diagramu skončí za okrajem, takže ji odřízneme. Naopak máme povoleno chodit podél okraje (v uctivé vzdálenosti D/2). Proto se podíváme na konce hran, které se zarazily o okraj, a zkusíme je propojit. Každá po sobě jdoucí dvojice takových hran ohraničuje společnou stěnu diagramu, uvnitř níž leží nějaký strom. Pokud je tento strom vzdálený od okraje aspoň D, můžeme mezi hranami projít podél okraje. To znázorníme dalším typem hran (na obrázku tečkované). Bude jich nejvýše O(S) a spočítáme je také v čase O(S).
Shrneme-li tyto úvahy (a doplníme spoustu detailů, o které jsme vás ošidili), získáme algoritmus řešící úlohu v čase O(S log S) bez jakýchkoliv požadavků na rozsah souřadnic a celočíselnost.
 28-3-8 Inteligence hejna (Zadání)
28-3-8 Inteligence hejna (Zadání)
Měli jsme za úkol hledat co nejkratší kružnici, která prochází všemi městy České republiky, přičemž text seriálu napovídal, že by se mohl použít mravenčí algoritmus. Tím to také zkusíme, ale nebude to úplně jednoduché. Úlohu budeme řešit jen pro všechna města. Pro jejich menší část by řešení bylo obdobné.
Část z vás se spletla a namísto kružnice hledala cestu. To ale nebyl velký problém. Myšlenka v následujících řešeních je v zásadě stejná, jen se na konci musíme vrátit do počátečního vrcholu.
Základní mravenčí algoritmus
První problém, na který můžeme narazit, je, že výpočet trvá hrozně dlouho. Průchod jednoho mravence přes všechna města může zabrat až vteřinu. To nás motivuje použít málo mravenců, protože chceme algoritmus nechat běžet více iterací a dozvědět se aspoň nějaký výsledek.
Abychom ušetřili aspoň trochu času, předpočítáme si matici vzdáleností měst, abychom je nemuseli počítat stále dokola.
Další problém může nastat s hodnotami vhodnosti hran bij a intenzitou feromonů fij. V textu seriálu se doporučuje dát bij = 1/dij, kde dij je délka hrany, a k fij přičítat hodnoty 1/L, kde L je délka nalezené cesty.
V praxi je dobré se snažit obě tyto hodnoty držet řádově stejné a při tom respektovat používané datové typy. Při spuštění algoritmu můžeme zjistit, že vzdálenosti měst se pohybují v rozmezí [501 ; 485 824], zatímco délky okružních jízd dosahují řádu 10 000 000. Pokud tedy použijeme bij = 1 000/dij a k fij budeme přičítat 107/L dostaneme se vždy zhruba do řádu jednotek.
Takto upraveným základním algoritmem spolu s parametry α=2, β=2 a vaporizací ρ= 0,5 jsem za několik desítek iterací a zhruba s jednotkami mravenců dosáhl řešení 23 495 526.
Vícekrát jsem to nespouštěl a ladit parametry se mi nechtělo, protože to běželo dost pomalu.
Hladový algoritmus
Teď chvíli zapomeneme na mravence a zkusíme úlohu vyřešit hladově. Začneme v náhodném městě a vždy se přesuneme do nejbližšího nenavštíveného města. Takto pokračujeme až dokud všechny neprojdeme. Kvalita řešení se může lišit v závislosti na výběru počátečního města. Tak se také vyplatí algoritmus spustit vícekrát.
Vašek Volhejn vyzkoušel pro hladový algoritmus všechny možné začátky a jako nejlepší řešení mu vyšlo 20 763 908.
Hladoví mravenci
A co takhle oba postupy zkombinovat? Nabízí se například vzít několik hladových řešení a vzít je jako počáteční populaci. Výpočet je ale stále pomalý a je jen malá šance, že tak hladové řešení překonáme. Hlavně bychom si museli trochu déle počkat.
Co uděláme my, je, že znovu použijeme mravenčí algoritmus, ale omezíme množství měst, ze kterých budeme vybírat následníka. Jelikož se pohybujeme v rovině, tak se nám takřka nikdy nevyplatí jít moc daleko. Další město můžeme tedy vybírat například z nejbližších K, kde K bude rozumně malé. Třeba 10.
Tím se algoritmus dost zrychlí. Už si můžeme dovolit použít více mravenců. Použijeme jich aspoň 100 až 1 000, aby v jedné iteraci zvládli označit rozumné množství hran feromony a další iterace tak měly větší variabilitu.
Pokud takové řešení s parametry α=2, β=2, ρ=0.5 a pro 1 000 mravenců necháme běžet 500 iterací (několik hodin), dostaneme se na řešení o hodnotě 20 550 678, což není o moc lepší než hladový algoritmus, ale aspoň něco. Tento algoritmus můžete vidět ve zdrojovém kódu.
Já pak ještě experimentoval s tím, že feromony zanechává jen W nejlepších mravenců z jedné iterace, ale dostal jsem se tak jen na víceméně stejně dobrý výsledek.
Další možné postupy
Evoluční a jim podobné algoritmy jsou většinou navržené obecně, aby se jimi dala řešit širší škála problémů. Proto nevyužívají charakteristiky žádného konkrétního z nich. Na jednu stranu je výhoda, že se dají prakticky vždy nějakým způsobem použít. Na druhou stranu ale mají nevýhodu v tom, že jsou málokdy nejlepší. Když se totiž zaměříme na konkrétní problém a navrhneme algoritmus přímo vhodný pro něj, tak obvykle dosáhneme vyššího úspěchu.
Kromě toho existují ještě heuristiky, které se snaží vylepšovat nějaké již existující řešení. Pro takové heuristiky se hodí jako počáteční řešení zvolit buď výsledek nějakého hladového algoritmu nebo právě výsledek některého z evolučních algoritmů.
Pro náš problém se dají použít například následující heuristiky:
- Prohodíme 2 hrany. Pokud se řešení zlepší, necháme je tak, jinak je vrátíme zpátky. (Díky této heuristice se postupně zbavujeme i křížení hran.)
- Prohodíme 3 hrany. Pakliže už nefunguje prohazování dvou hran, můžeme začít prohazovat 3, což nám dává další možnosti.
- Přeházení K po sobě jdoucích měst. Také může pomoci.
U všech těchto heuristik nové řešení přijmeme pouze pokud nám heuristika pomohla. Tyto heuristiky uvádíme jen pro příklad. Ty nijak nesouvisí s evolučními algoritmy. Pomocí nich se řešení dalo vylepšit až na 18 000 000.