Pátá série dvacátého osmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 28-5-1: Zaměřování místnosti
- 28-5-2: Místní přesuny
- 28-5-3: Trezor s alarmem
- 28-5-4: Časoprostorové mosty
- 28-5-5: Kalibrace
- 28-5-6: Sloty na iridium
- 28-5-7: Tajemná operace
- 28-5-8: Neuronové sítě
 28-5-1 Zaměřování místnosti (Zadání)
28-5-1 Zaměřování místnosti (Zadání)
Nejprve si všimneme, že pokud obdélník existuje, pak nějaké dva body z libovolné pětice určují jednu stranu obdélníku. To vyplývá z tzv. Dirichletova principu (neboli principu holubníku), který v tomto případě říká, že pokud máme pět bodů, které leží na čtyřech stranách, tak nutně na alespoň jedné straně jsou alespoň dva body.
Vezmeme tedy dva body z náhodně vybrané pětice a zkusíme, jestli s jednou stranou určenou touto dvojicí bodů obdélník existuje. (Jak přesně to zjistíme, je vysvětleno v následujícím odstavci.) Když chceme vybrat dva body z pěti, máme celkem deset možností, jak to udělat. Proč? Pokud znáte kombinační čísla, tak jistě dokážete spočítat, že vybíráme-li dva z pěti bodů, možností, jak to udělat, je deset.
Pokud vám kombinační čísla nic neříkají, stačí jednoduchá úvaha: je pět možností, jak vybrat první bod, a pro každou z těchto pěti možností jsou ještě čtyři další, jak k nim vybrat druhý bod. Pět krát čtyři je tedy dvacet možností, když víme, jaký bod byl vybrán první a jaký druhý. Nám ale na jejich pořadí nezáleží a můžeme je mezi sebou zaměnit. Tedy dvacet vydělíme dvěma a dostáváme, že způsobů, jak vybrat dva z pěti bodů, když nezáleží na pořadí, je deset.
Teď si ukážeme, jak s libovolnou dvojicí bodů postupovat. U ostatních bodů zkontrolujeme, zdali neleží na této první přímce také. Pokud ano, můžeme je pro teď zapomenout. Pro všechny zbylé body si spočítáme vzdálenost od první přímky. Body (nebo bod) s největší vzdáleností budou ležet na opačné straně obdélníka a také je můžeme pro teď odstranit. Zbylé body by tedy měly ležet na nejvýše dvou přímkách kolmých na dosud určené přímky. Navíc musí být tyto kolmé přímky od sebe vzdálené alespoň tak, jak jsou od sebe vzdálené krajní body na původních přímkách, tak aby tvořily obdélník.
Pro každou dvojici tedy provedeme řádově N operací, kde N je počet bodů celkem. Různých dvojic je celkem deset, složitost je tak 10N, tedy O(N) – lineární.
Zbývá vyřešit případy, kdy je bodů méně než pět. Pokud jsou body tři a méně, lze obdélník sestrojit vždy. Pokud jsou body čtyři, můžeme si pomoci například sestrojením konvexního obalu. Pokud na něm nějaký bod neleží, obdélník existovat nemůže.
Někteří zvolili k celému řešení úlohy sestrojení konvexního obalu a následně jej různě využili ke zjištění, zda jde o obdélník, nebo ne. Většina nápadů nebyla špatná a fungovala by, ale sestrojit konvexní obal trvá O(N log N), a je to tedy pomalejší než výše popsané lineární řešení. Jediný řešitel, který správné lineární řešení poslal, byl Tomáš Domes, kterého tímto chceme veřejně pochválit.
 28-5-2 Místní přesuny (Zadání)
28-5-2 Místní přesuny (Zadání)
Nejprve si uvědomíme, že se žádný bod nevyplatí navštívit dvakrát. Druhou návštěvu můžeme vynechat, a tím si cestu vždy zkrátíme:
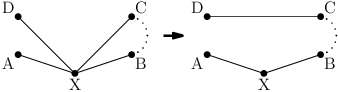
Z trojúhelníkové nerovnosti |CD| < |CX| + |XD| tedy upravená cesta musí být kratší. Hledáme tedy nejkratší hamiltonovskou cestu v úplném grafu, jehož vrcholy jsou naše body a hrany úsečky spojující každou dvojici bodů. To je cesta, která navštíví každý vrchol právě jednou. Pro obecné grafy je její nalezení těžký problém, ale ukážeme si, že v případě vrcholů v konvexní poloze to neplatí.
Dále si všimneme, že optimální cesta nikdy nekříží sebe sama. Uvažujme libovolnou cestu, na které se kříží nějaké dvě hrany AB, CD. Označme si P jejich průsečík. I takovou cestu snadno zkrátit:
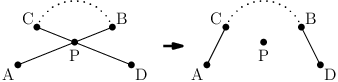
Opět z trojúhelníkové nerovnosti: |AC| < |AP| + |CP|, |BD| < |PD| + |PB|. Sečtením dostáváme |AC| + |BD| < |AP| + |PB| + |CP| + |PD| = |AB| + |CD|, tedy nová cesta je kratší než původní.
Nyní k samotnému algoritmu. Začneme tím, že si vrcholy očíslujeme v pořadí, v jakém leží na obvodu konvexního mnohoúhelníku. K tomu můžeme použít libovolný algoritmus pro hledání konvexního obalu. Protože máme body v konvexní poloze, budou všechny patřit do nalezeného konvexního obalu, ten nám ale navíc určí jejich pořadí. Zvládneme to v čase O(N log N).
Očíslování budeme chápat jako cyklické a s čísly vrcholů pracovat modulo N, tedy např. 0-1 = N-1. Pak sousedé libovolného vrcholu X jsou X+1 a X-1.
Označení úlohy jako kuchařkové napovídá, že chceme použít dynamické programování. Abychom to mohli udělat, musíme úlohu rozdělit na menší podproblémy, z řešení kterýchž lze poskládat řešení původního většího problému.
Na první pohled se zdá, že vhodným podproblémem by mohlo být hledání nejkratší cesty pokrývající nějaký souvislý úsek vrcholů mnohoúhelníka. Takový úsek můžeme identifikovat dvěma čísly (a, b) udávajícími počáteční a koncový vrchol. Pozor, že pokud jde úsek „přes nulu“, může být b<a. Na následujícím obrázku je zvýrazněn úsek (5, 2) tvořený vrcholy 5, 0, 1, 2 a nejkratší cesta jej pokrývající:
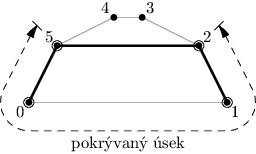
Na obrázku vidíme další problém: takováto nejkratší cesta je nám k ničemu, protože ji nedokážeme bez křížení prodloužit na nejkratší cestu pokrývající nějaký delší úsek. Aby se na cestu dalo ještě něco napojit, musí mít alespoň jeden konec v krajním bodě intervalu (zde 5 nebo 2).
Zkusme si tedy zesílit zadání: pro každý úsek (a, b) budeme hledat hned dvě cesty. První z nich bude nejkratší cesta navštěvující všechny vrcholy úseku a končící v a. O tom, kde má druhý konec, nic neříkáme. Může to být v b, ale taky někde uprostřed úseku. Označíme si ji P1(a, b), její délku pak D1(a, b). Analogicky P2(a, b) bude nejkratší pokrývající cesta končící v b.
Snadno si navíc rozmyslíte, že ani jedna z těchto cest nikdy nenavštíví vrchol mimo požadovaný úsek (protože takovou nepovinnou návštěvu můžeme vynechat, a tím cestu zkrátit). Může se stát, že P1(a, b) = P2(a, b), ale obecně nemusí. Vše je vidět na následujícím obrázku.
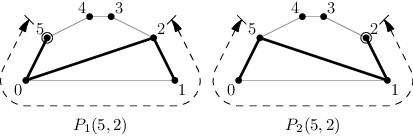
Pro jednoduchost budeme počítat jen délku nejkratší cesty, nalezení cesty samotné se snadno doplní. Jak spočítáme např. D1(a, b)?
Uvažujme poslední hranu cesty P1(a, b), končící v a. To může být buď strana mnohoúhelníka, nebo úhlopříčka. Pokud je to strana, musí vést do vrcholu a+1 (na obrázku 0). Vrchol a-1 (4) leží mimo pokrývaný úsek a výše jsme ukázali, že takové se navštívit nevyplatí.
Po odebrání poslední hrany P1(a, b) dostaneme nějakou cestu pokrývající o jedna kratší úsek, (a+1, b), která navíc končí v a+1. A musí to být nejkratší taková, tedy dlouhá D1(a+1, b). Kdyby byla delší, můžeme ji zkrátit výměnou za P1(a+1, b).
Pokud je poslední hrana úhlopříčka, musí naopak vést do vrcholu b. Kdyby vedla kamkoli jinam, rozdělí nám pokrývanou část mnohoúhelníka na dvě poloviny, mezi kterými nelze přejít bez křížení cest. Představte si na obrázku výše, co by se stalo, kdyby cesta končila hranou (1, 5). Analogicky po odebrání poslední hrany dostaneme nějakou cestu pokrývající zbylý úsek, ale tentokrát končící v b.
To jsou jediné dvě možnosti, jak může P1(a, b) vypadat. Pak stačí vybrat tu kratší:
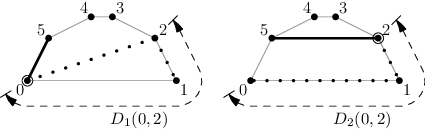
Dostáváme jednoduchou rekurenci:
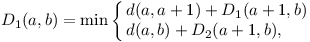
Pro D2 to dopadne analogicky. Nyní stačí hodnoty D1 a D2 spočítat pro všech N2 dvojic dynamickým prograováním. Jeden výpočet trvá konstantně dlouho, takže vše zvládneme v čase O(N2). Nakonec stačí z nalezených cest pokrývajících celý mnohoúhelník (rozmyslete si, že to jsou právě D1(a, a-1) a D2(a, a-1) pro všechna a) vybrat tu nejkratší.
Spotřebujeme též kvadratické množství paměti. Ale pokud bychom si namísto nejkratší cesty vystačili s její délkou, můžeme paměťovou složitost zlepšit na lineární. Všimneme si totiž, že kdykoli během výpočtu si stačí pamatovat poslední dvě patra rekurze. Když počítáme hodnoty pro úseky délky k, stačí nám k tomu znát hodnoty pro úseky délky k-1. Všechny kratší můžeme zahodit.
 28-5-3 Trezor s alarmem (Zadání)
28-5-3 Trezor s alarmem (Zadání)
Aby sa nám lepšie s grafom pracovalo, tak ho na začiatku prečistíme. Odstránime si z neho vrcholy (a k ním pripojené hrany), ktoré neležia na žiadnej ceste zo z do k. Je zrejmé, že vrcholy na odstránenie budú práve tie, z ktorých nevedie cesta do k, a tie, do ktorých sa zo z nedá dostať. Žiadne ďalšie to byť nemôžu, lebo vrchol, do ktorého sa dá dostať zo z a zároveň z neho vedie cesta do k, tvorí cestu zo z do k. Graf, ktorý ostane po tomto prečistení, si označme ako G', jeho počet vrcholov N' a hrán M'.
Graf G' je naďalej orientovaný a neexistuje v ňom ani žiaden orientovaný cyklus (odstraňovaním vrcholov a hrán cyklus vzniknúť nemôže). Teda vrcholy grafu G' je možné topologicky zoradiť. To znamená, že vrcholy sa očíslujú od 1 do N', a to tak, že každá orientovaná hrana bude viesť vždy od vrcholu s menším číslom do vrcholu s väčším číslom. Všimnime si, že z dostane číslo 1 a k číslo N', lebo žiaden vrchol nemôže byť väčší ako k a žiaden menší ako z.
Posledný krok bude v grafe G' nájsť kritické vrcholy. Vrchol v bude kritický práve vtedy, keď nebude existovať žiadna hrana vedúca od vrcholu s číslom menším ako v do vrcholu s číslom väčším ako v. Ak by takáto hrana existovala, potom cesta zo z do k, ktorá obsahuje túto hranu nemôže zároveň obsahovať vrchol v (kvôli topologickému usporiadaniu vrcholov). Zároveň vrchol, ktorý neobchádza žiadna hrana, sa bude nachádzať na každej ceste zo z do k, keďže ako jediný spája vrcholy s menšími číslami ako je on sám a s väčšími číslami ako je on sám.
Ostáva nám už iba popis algoritmov na jednotlivé časti rozboru. Prečistenie grafu spravíme dvojitým prehľadaním grafu do hĺbky. Prvý spustíme zo z a označíme si dosiahnuteľné vrcholy po smere hrán. Druhý spustíme z k, ale proti smeru orientácií hrán, čím získame vrcholy, z ktorých sa dá dostať do k. To zvládneme v čase O(N+M), lineárne od počtu hrán a vrcholov v G. Topologické zoradenie vrcholov acyklického orientovaného grafu vieme uskutočniť taktiež v čase O(N+M), napríklad pomocou algoritmu z našej kuchárky o rovinných grafoch.
V poslednom kroku už budeme mať dostupný topologicky zoradený zoznam vrcholov grafu G'. Tento zoznam vrcholov budeme postupne spracovávať od najmenšieho po najväčší. Pri spracovávaní si budeme pamätať a priebežne aktualizovať maximálne číslo m. To bude reprezentovať najvzdialenejší vrchol od začiatku, na ktorý už viedla nejaká hrana.
Spracovávanie každého vrcholu začneme porovnaním čísla tohoto vrcholu a hodnoty m. Ak sú hodnoty rovnaké, potom bude aktuálny vrchol kritický. Platí to, pretože neexistuje hrana zo žiadneho vrcholu s menším číslom ako m do vrcholu s väčším číslom ako m. Následne sa pozrieme na všetkých susedov spracovávaného vrcholu. Vždy, keď bude číslo niektorého suseda väčšie ako m, tak zmeníme m práve na číslo toho suseda. Týmto docielime, že na konci spracovávania vrcholu, bude v m opäť najväčšie číslo, do ktorého sa vieme dostať.
Aby sa nám spracovávanie zoznamu vrcholov nedostalo do nedefinovaného stavu, tak si na začiatku nastavíme hodnotu m na 1. Zároveň budeme ignorovať informáciu, že kritický vrchol by mal byť aj z (rovný 1) a aj k (najväčší). Tie v skutočnosti netvoria uzly sústavy obvodov zo zadania.
Posledný krok zvládneme taktiež v čase O(N+M), keďže každý vrchol a každú hranu spracujeme práve raz. Teda celková časová zložitosť bude lineárna od súčtu počtu hrán a vrcholov vo vstupnom grafe G. Ak použijeme klasickú reprezentáciu grafu G a G' ako zoznam susedov pre každý vrchol, tak rovnako bude na tom aj pamäťová zložitosť.
 28-5-4 Časoprostorové mosty (Zadání)
28-5-4 Časoprostorové mosty (Zadání)
Pro řešení této úlohy existuje poměrně jednoduchý, leč neefektivní algoritmus: Po každém odstranění mostu zkontrolujeme graf prohledáním vrcholů, zda se komponenta obsahující tento most rozpadla na dvě.
Tento způsob určitě funguje, ale je velmi pomalý. Každé odstranění mostu znamená O(N) operací, tedy celkově tento algoritmus zabere až O(M·N) času. Nejvíce nás zdržuje právě zjišťování, zda odstranění daného mostu způsobilo rozpad komponent. Jak z této neefektivity vybruslíme?
Pojďme se na chvíli podívat na algoritmy pro hledání nejmenších koster, konkrétněji Kruskalův algoritmus, o kterém se lze více dočíst v kuchařce o kostrách. Jeho princip spočívá v tom, že postupně bere nejlevnější hranu. Poté se ptá, zda její přidání do kostry způsobí sloučení dvou komponent do jedné. A to je přesně opačný problém.
K tomuto problému existuje datová struktura Union-Find, která poskytuje dvě hlavní operace:
- Union spojí dvě komponenty určené vrcholy A a B.
- Find pro dva vrcholy A a B odpoví, zda tyto vrcholy leží ve stejné komponentě souvislosti.
O tom, jak tato datová struktura funguje a jak je složitá, si můžete více přečíst ve výše zmíněné kuchařce.
Jak nám ale tato datová struktura pomůže? Dělá přece opak toho, co chceme. Nezoufejme však, jelikož můžeme použít chytrý trik. Vzhledem k tomu, že známe dopředu posloupnost odstranění mostů, můžeme celý postup obrátit. Začneme s grafem podle toho, jak vypadá po odstranění všech mostů a postupně voláme operace Union a Find.
Findem zjistíme, zda most vede uvnitř jedné komponenty. Pokud ano, nemusíme dělat nic. Jinak Unionem komponenty sloučíme, sečteme jejich energie a součet prohlásíme za energii nové komponenty. Takto postupujeme, dokud nepřidáme všechny mosty. Nakonec vypíšeme výsledek jednotlivých operací pozpátku.
Celkově nás tedy odebrání (přidání) jednoho mostu stojí tolik času, co provedení operací Union a Find. To je pro dostatečně slušnou implementaci této datové struktury O(log N). Dohromady má tedy celý algoritmus časovou složitost O(M log N).
Poznámka M.M.: Složitost O(log N) pro Union-Find je velmi velkorysá. Ve skutečnosti i jednoduchá implementace struktury pomocí stromečků, kterou popisujeme v kuchařce, pracuje daleko efektivněji. Složitost lze omezit například funkcí O(log *). Tento „hvězdičkový logaritmus“ je definovaný jako funkce inverzní k takzvané věžové funkci:
Funkce log * n tedy roste velice pomalu, ale ani ona není nejlepší možná. Více už zde neprozradíme a raději vás odkážeme na detaily v kuchařce.
 28-5-5 Kalibrace (Zadání)
28-5-5 Kalibrace (Zadání)
Máme původně setříděnou posloupnost N čísel, která se zrotovala o neznámý počet pozic, a přesně tento počet bychom chtěli určit. Než se do toho pustíme, podotkněme, že čísla už máme skutečně uložená v paměti. Nemusíme se tedy starat o načtení vstupu (to v praxi odpovídá třeba tomu, že píšeme ne celý program, ale nějakou funkci).
Pravděpodobně nás záhy napadne použít nějakou formu binárního vyhledávání, které je popsané třeba v kuchařce základních algoritmů.
Co s ním ale budeme hledat? Špatně uspořádanou dvojici čísel. Můžeme si rozmyslet, co dostaneme, když zrotujeme posloupnost doprava. Na začátku bude nějaký správně uspořádaný kus, pak špatně uspořádaná dvojice (konkrétně největší prvek následovaný nejmenším) a pak zase správně uspořádaný kus.
Budeme tedy hledat tohle špatné uspořádání, přesněji druhé z těchto špatně uspořádaných čísel. Jeho pozice nutně odpovídá rotaci (počtu pozic, o které byla posloupnost zrotovaná).
V každém kroku se díváme na úsek. Nejprve porovnáme levý krajní prvek L a pravý krajní prvek R tohoto úseku. Je-li R > L, úsek je správně uspořádaný. Pokud víme, že v něm je špatně uspořádaný prvek, musí být hned na začátku a můžeme vrátit pozici L.
V opačném případě se podíváme na prostřední prvek M. Je-li M > L, první polovina je správně uspořádaná. Problém tedy bude ve druhé, takže se zanoříme do pravé poloviny. Pro M < L naopak. Dostaneme-li se k úseku velikosti 1, určitě je problematickým prvkem právě ten jediný v něm.
Voilà, máme algoritmus, který najde problematickou pozici. Jelikož vždy rozdělíme aktuální úsek alespoň na polovinu, skončíme nejpozději po log N krocích. Časová složitost algoritmu je tak O(log N).
Paměťová složitost je O(N), pokud uvažujeme uloženou posloupnost. Můžeme ale říct, že tak jako zanedbáváme načtení vstupu, zanedbáme uložení posloupnosti, a pak je paměťová složitost konstantní, O(1).
 28-5-6 Sloty na iridium (Zadání)
28-5-6 Sloty na iridium (Zadání)
Rozmísťování iridia do slotů se ukázalo být zapeklitějším problémem, než se zprvu zdálo. Většina z odvážných, kdo se úloze vydali vstříc, vyřešila první triviální vstup, ale přes druhý už se dostal jen jediný z vás (gratulujeme tímto Jirkovi Sejkorovi) a dál už se nedostal vůbec nikdo.
Vstupy se postupně zvětšovaly, ale některé z nich měly i jisté speciální vlastnosti. Třeba pátý vstup měl na pár místech veliké mezery a nebo hned třetí vstup měl všechny dostupné sloty rozmístěné jenom v jedné polovině obvodu. Zvlášť možností využít jen jednu polovinu obvodu se úloha pěkně zjednodušila, protože se pak problém choval jako rozmísťování iridia do slotů na přímce namísto kružnice. Vyřešme si tento jednodušší problém.
Sloty na přímce
Pokud budeme mít sloty na přímce, můžeme bez obav umístit iridium do prvního slotu, protože tím nic nepokazíme (pokud by v nějakém optimálním rozmístění nebylo první iridium v prvním slotu, můžeme ho bez zhoršení minimálních vzdáleností do prvního slotu posunout).
Nyní vyzbrojeni tímto pozorováním zkusme vyřešit úlohu trošku odlišnou – totiž otázku, jestli pro zadanou minimální vzdálenost d lze rozmístit iridium do slotů tak, aby byla tato minimální vzdálenost dodržena. Až vyřešíme tuto úlohu, ukážeme si, jak nám pomůže vyřešit původní problém.
Z pozorování výše víme, že první iridium můžeme umístit do prvního slotu a nic si tím nepokazíme. Další iridium můžeme umístit nejblíže ve vzdálenosti d. Takže přeskočíme všechny bližší sloty a iridium umístíme do prvního slotu, který má vzdálenost větší nebo rovnou d.
A tímto způsobem postupujeme dál, plníme vlastně sloty hladově zleva. Pokud se nám takto povede všechno iridium umístit, zahlásíme úspěch, pokud nám ale dojdou sloty a ještě nám bude zbývat neumístěné iridium, tak víme, že rozmístit s touto vzdáleností nejde (žádné iridium již nelze posunout více doleva, abychom si na konci uvolnili nějaké sloty).
V čase O(S) tedy umíme lineárním průchodem přes sloty vyřešit tuto podúlohu (připomeňme, že S je počet dostupných slotů). Jak nám to pomůže se řešením původního problému? Můžeme zkusit najít největší vzdálenost, pro kterou se nám ještě iridium povede rozmístit, a toto rozmístění pak vypsat. Hledání největší vzdálenosti můžeme dělat postupným zvětšováním o jedničku a zkoušením, ale to by pro obvod O trvalo až O(OS) a to je moc dlouho.
Víme, že se tento problém hledání vzdálenosti chová lineárně – když pro nějakou vzdálenost rozmístění iridia existuje, tak existuje i pro všechny menší vzdálenosti, když naopak neexistuje, tak neexistuje ani pro žádnou větší vzdálenost. Můžeme tedy maximální možnou vzdálenost binárně vyhledat.
| min+max |
| 2 |
- Pokud se iridium povede rozmístit → hledaná vzdálenost je větší nebo rovna d, nastavíme min=d
- Pokud se iridium nepovede rozmístit → hledaná vzdálenost je menší než d, nastavíme max=d-1
Takto pokračujeme, dokud nedojdeme na krok velikosti jedna. Pak již máme vzdálenost určenou jednoznačně. Binárním vyhledáváním uděláme O(log O) kroků, takže celkově dosáhneme času O(S log O).
Sloty na obvodu kruhu
Při rozmisťování iridia do slotů na obvodu kruhu použijeme úplně stejný postup, jen se už nemůžeme spolehnout na pozorování o umístění prvního iridia do prvního slotu. Nyní totiž jde i o vzdálenost prvního a posledního obsazeného slotu. Může být například výhodné prvních pár slotů přeskočit, aby nám vzdálenost vyšla.
Jak si s tím poradit? Pokud nám při zkoušení, jestli iridium umíme rozmístit se vzdáleností d, dojdou sloty před rozmístěním všech kousků, můžeme rovnou oznámit neúspěch. Pokud se nám naopak iridium rozmístit povede a vzdálenost mezi prvním a posledním obsazeným slotem je dostatečně velká, můžeme rovnou oznámit úspěch. To byly ty jednodušší případy.
Složitější je, pokud sice všechno iridium rozmístíme, ale vzdálenost mezi prvním a posledním bude příliš malá. Pak můžeme zkusit první posunout po obvodu dál tak, abychom tuto vzdálenost dostatečně zvětšili. Pokud tím neporušíme minimální vzdálenost k dalšímu obsazenému slotu, uspěli jsme, jinak to samé opakujeme (opět posuneme další iridium tak daleko, aby byla dodržená minimální vzdálenost a opakujeme).
Toto posouvání zastavíme ve chvíli, kdy se nám rozmístění buď povede opravit (v tom případě oznámíme úspěch), nebo když se pokusíme nějaké iridium umístit opět do prvního slotu. V tom případě totiž opět dostáváme stejnou situaci, jako při prvním rozmístění, a zacyklili jsme se bez nalezení fungujícího rozmístění.
Na implementaci tohoto postupu se můžete podívat v ukázkovém programu, nyní se zamysleme nad časovou složitostí. Hlavní pozorování je, že se při posouvání iridia mezi sloty pokusíme vložit iridium do každého ze slotů maximálně dvakrát. Při druhém pokusu o vložení do stejného slotu totiž dojde k tomu, že se i všechny zbylé kousky rozmístí tak, jak byly, a dojde k zacyklení (při kterém se zastavíme s neúspěchem).
Čas jednoho kroku jsme si tak oproti jednodušší verzi na přímce zhoršili jen konstantně a vnější část s binárním vyhledáváním zůstává stejná. Celkově tak dosáhneme časové složitosti O(S log O).
 28-5-7 Tajemná operace (Zadání)
28-5-7 Tajemná operace (Zadání)
Zopakujme si zadání: Dostaneme nějakou magickou operaci ⊗ a posloupnost a1,… ,an. Chceme si něco předpočítat, abychom uměli vyhodnocovat intervalové dotazy typu ai ⊗ai+1 ⊗… ⊗aj a stačilo nám jediné zavolání operace ⊗.
Pochopitelně si můžeme předpočítat výsledky pro úplně všechny intervaly ai,… ,aj. Pak při odpovídání na dotazy dokonce nemusíme ⊗ volat vůbec. Ovšem předvýpočet trvá čas O(n2), což nám nepromine sebetrpělivější uživatel, natož pak přísné elektronické oko CodExovo.
Tak zkusíme sáhnout po různých standardních technikách, jako je třeba rozklad na bloky nebo intervalové stromy. Z těch také použitelné řešení nekápne: na kombinování bloků nebo podstromů sice postačí malý počet volání ⊗, ale rozhodně více než povolené jedno. Přesto z myšlenky rekurzivního rozkladu na podproblémy něco vykřešeme. Tedy poslyšte…
Rekurzivní řešení
Učiníme myšlenkový pokus: zadanou posloupnost rozdělíme přibližně uprostřed na levou polovinu a1,… ,as a pravou polovinu as+1,… ,an. Dotazy rozdělíme na dva druhy podle toho, zda leží přes střed, či nikoliv.
Pokud interval ai,… ,aj jde přes střed, skládá se ze suffixu levé poloviny (to je nějaký interval ai,ai+1,… ,as) a prefixu té pravé (as+1,… ,aj). Předpočítáme-li si tedy výsledky pro všechny suffixy levé poloviny a všechny prefixy pravé, umíme je na jedno zavolání ⊗ složit do výsledku celého dotazu.
A pokud interval neleží přes střed, přesuneme se do levé či pravé poloviny a tam rekurzivně aplikujeme tentýž postup. Pojďme spočitat, jak je to efektivní.
Označme P(n) časovou složitost předvýpočtu pro posloupnost délky n. Jistě platí, že P(n) = 2·P(n/2) + O(n), neboť pro interval délky n v čase O(n) zpracujeme prefixy a suffixy a rekurzivně předpočítáme zvlášť levou a pravou polovinu. Tuto rovnici pro P(n) můžeme vyřešit třeba analýzou stromu rekurze. Raději použijeme prostý trik: všimneme si, že úplně stejně se chová známý algoritmus MergeSort (třídění sléváním) – také spotřebuje lineární čas a pak rekurzivně zpracuje dva poloviční podproblémy. MergeSort běží v čase O(n log n), takže náš předvýpočet také.
Vyhodnocování dotazu buďto skončí ihned (jde-li dotaz přes střed), nebo se rekurzivně zavolá na jednu z polovin. Během O(log n) kroků tedy rekurze musí skončit. Jelikož každý krok trvá konstantně dlouho, časová složitost dotazu činí celkem O(log n). Podmínku na nejvýše jedno použití ⊗ jistě splňujeme.
Rychlejší řešení
Nevýhodou předchozího řešení je, že vyhodnocení dotazu sice volá ⊗ jenom jednou, ale kromě toho tráví logaritmický čas nalezením správného podintervalu, přes jehož střed zadaný dotaz leží. To lze s trochou šikovnosti zvládnout i v konstantním čase.
Předně si představujme, že délka posloupnosti je mocnina dvojky a že prvky očíslujeme od nuly: a0,… ,an-1. Pokud se na indexy prvků podíváme ve dvojkové soustavě, v levé polovině všechny začínají nulou, v pravé jedničkou. Dotaz tedy leží přes střed právě tehdy, pokud se jeho levý a pravý okraj liší v nejvyšším bitu.
Rekurzivní rozklad intervalů můžeme elegantně popsat binárním stromem, který na h-té hladině testuje h-tý nejvyšší bit čísla. Nejvyšší interval, v němž jde dotaz přes střed, pak odpovídá nejvyššímu bitu, v němž se okraje dotazu i a j liší. To je nejvyšší jedničkový bit v čísle ixor j. Pro zjišťování, kde leží nejvyšší jednička, si přitom můžeme snadno předpočítat tabulku.
Celkově tedy v konstantním čase spočítáme ixor j, pomocí tabulky zjistíme hladinu h stromu rekurze, kam se chceme podívat. A nejvyšších h bitů čísel i a j nám řekne, kolikátý vrchol zleva nás na dané hladině zajímá. Vrcholy tedy můžeme mít uložené v poli a indexovat je též v konstantním čase.
Rozklad na bloky
Pro zajímavost načrtneme ještě jedno řešení pomocí rozkladu na bloky. To je nejspíš jednodušší na vymyšlení, ale o něco pomalejší.
Posloupnost rozřežeme na √n bloků velikosti √n. Dotazy, které leží celé uvnitř jednoho bloku, předpočítáme všechny. Je jich O(n) na blok, celkem tedy O(n3/2).
Ostatní dotazy chceme skládat ze suffixu prvního bloku, nějakých celých bloků a prefixu posledního bloku. Suffixy a prefixy si můžeme předpočítat (je jich celkem O(n)). Nabízí se předpočítat si také všechny intervaly celých bloků (těch je též O(n)), ale s tím narazíme: na zodpovězení dotazu bychom potřebovali složit tři mezivýsledky, tedy zavolat operaci ⊗ dvakrát, což je moc.
Proto si místo obyčejných suffixů předpočítáme všechny intervaly, které vzniknou rozšířením suffixu o nějaký počet celých bloků. Každý suffix má √n takových rozšíření, úplně všechny suffixy pak O(n3/2). Pak stačí skládat rozšířený suffix s obyčejným prefixem.
Získali jsme tedy řešení s předvýpočtem v čase O(n3/2) a dotazem v čase O(1) s jedním voláním operace ⊗.
Cesta jde pořád dál a dál…
Na závěr ještě dodejme, že kdybychom povolili větší (ale stále konstantní) počet použití ⊗, úloha by byla mnohem zajímavější, ovšem také mnohem náročnější. Například pro 3 volání ⊗ stačí předzpracování v čase O(n log * n), kde log * je funkce zmíněná v řešení čtvrté úlohy.
 28-5-8 Neuronové sítě (Zadání)
28-5-8 Neuronové sítě (Zadání)
Úkol 1
Cílem první úlohy je nalézt co nejmenší neuronovou síť modelující XOR. Překvapilo nás, že žádné ze zaslaných řešení nebylo optimální, takže tady je:
Důkaz minimality provedeme sporem. Kdyby byla síť ještě menší, měla by jen dva vstupní a jeden výstupní neuron bez skryté vrstvy. Jeden neuron dokáže, stejně jako perceptron, v dvourozměrném vstupním prostoru oddělovat dvě skupiny vzorů přímkou, jak jsme psali v minulém dílu seriálu. U funkce XOR ale vstupní vzory přímkou oddělit nelze, říkáme, že nejsou lineárně separovatelné. To ilustrují následující dva grafy lineárně separovatelné množiny a množiny možných vstupů xoru.
Úkol 2
Druhým úkolem bylo implementovat neuronovou síť pro klasifikaci kosatců. Na následujícím odkazu si můžete stáhnout vzorové řešení v jazyce Python. Náš program využívá neuronovou síť o 3 skrytých neuronech v jedné skryté vrstvě a dosahuje přesnosti klasifikace na validační množině kolem 98% až 100%.
Úkol 3
Poslední úlohu bylo možné řešit pomocí zpětné propagace nebo navrhnout síť pomocí analytické geometrie. Jelikož zpětnou propagací jsme řešili minulou úlohu a používala ji i všechna vaše řešení, podíváme se na geometrický přístup. Kolem srdce zkonstruujeme „obal“ z několik přímek, které budou oddělovat body uvnitř obrazce od ostatních. Tyto přímky pak převedeme na neurony, které budou dělat totéž v rámci neuronové sítě.
Z analytické geometrie víme, že přímka má rovnici y = ax + b, také víme, že a se dá spočítat pomocí úhlu α, který přímka svírá s osou x: a = tan(α). Hodnotu b pak můžeme dopočítat dosazením nějakého bodu na přímce do rovnice přímky. Díky tomu můžeme spočítat rovnice všech osmi v obrázku zakreslených přímek. Ukažme si to na pravé spodní přímce, která má sklon 45° a leží na ní bod [0;0]:
| a | = tan(α) = tan(45°) = 1 |
| y | = x + b |
| 0 | = 0 + b |
| b | = 0 |
Tuto rovnici přímky nyní můžeme upravit do tvaru 0 = ax - 1y + b a porovnáním s rovnicí neuronu 0 = ξ= w1x + w2y + δ z ní určit jeho váhy w a práh δ. Pro naši první přímku y = x + 0 to bude w = [1; -1] a δ= 0. Všimněte si, že nemáme zajištěno, na které straně přímky bude potenciál neuronu kladný a na které záporný. V tomto případě bude kladný v oblasti mimo srdce. Pokud bychom chtěli hodnoty prohodit, můžeme vynásobit uvedenou rovnici neuronu -1, čímž dostaneme váhy a práh také vynásobený -1.
Tímto postupem můžeme určit váhy a prahy neuronů všech osmi přímek. Řekněme, že tedy máme neurony s aktivační funkcí signum, které mají pro body směrem dovnitř obrazce kladný výstup +1. Bod je uvnitř srdce tehdy, když všechny neurony mají kladný výstup, kromě dvou neuronů, jejichž přímky jsou na obrázku vykresleny přerušovanou čarou. Z těch stačí jeden s výstupem +1.
Abychom tuto podmínku realizovali neurony, pořídíme si vrstevnatou neuronovou síť jako na následujícím obrázku. Neurony přímek jsou použity v první skryté vrstvě. Aktivační funkce všech neuronů je signum. Nezakreslené hrany můžeme v síti formálně ponechat s nastavenou váhou 0 (ilustrováno přerušovanou čarou).