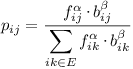Třetí série dvacátého osmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Zadání úloh

Gaius Fabius nebyl z tažení, které odvedlo legii od jeho rodné Florencie daleko na sever do barbarské Galie, vůbec nadšený. Jednak se nerad vzdaloval od své ženy a syna, ale taky se úplně nehrnul do předních řad. Pocit stát v čele a cítit, jak se o široký štít odrážejí meče barbarů, rád přenechal jiným. Gaius se raději nacházel v pozadí a jako řemeslník se staral o spoustu věcí od obléhacích strojů po stavbu opevnění.

Tento den legie dopochodovala na planinu v lese, legát vyslal průzkumníky a zbytek se dal do stavby opevnění. Teprve před chvílí vztyčili poslední část dřevěného opevnění a Gaius unaveně padl na zem vedle ohně.

Část legionářů tu zrovna hrála hru se svými helmicemi. Stavěli z nich pyramidy a štouchali do nich kopím.

Teoretická úloha28-3-1 Pyramida z helmic (7 bodů)

Římští legionáři hrají o to, kdo bude mít v noci hlídku. Vždy hrají dva proti sobě, poberou si spoustu helmic a poskládají z nich pyramidu vysokou h (spodní patro má h helmic, patro nad ním h-1, …).

Do každé helmice navíc vloží nějaký počet kamínků – do vrchní helmice přijde jeden a do každé další pak tolik kamínků, jako v helmicích vlevo a vpravo nad ní dohromady (pokud takové helmice jsou). Počet kamínků v helmicích tedy odpovídá Pascalově trojúhelníku a následujícímu obrázku:

Kamínky v helmicích

Legionáři se střídají po tazích. Vždy jeden z nich strčí kopím do helmice, kterou si vybere, a tím shodí ji i všechny helmice stojící na ní (levou vrchní, pravou vrchní a všechny, co podobně stojí na nich). Ze shozených helmic dostane všechny kamínky.

Hraje se tak dlouho, dokud stojí alespoň jedna helmice. Vyhrává ten, který má na konci méně kamínků. Existuje vyhrávající strategie pro některého z hráčů? A jak vypadá?

Řešení

Hlídku „vyhráli“ Brutus a Marcus a ostatní vojáci centurie šli spát. Gaius měl jako řemeslník výhodu, že mohl spát ve svém stanu, který představoval vlastně i malou dílnu.

Zabalený pod přikrývky v tomto mrazivém počasí skoro usnul, když ho probudila podivná rána, takové lupnutí. Převalil se na bok a v tom ho uviděl! Divná postava, po níž ještě přebíhali nějací modří hadi. A v jeho stanu! Bohové!

Postava, asi muž, se zprudka nadechla a potřásla hlavou. Pravou rukou něco udělala na své levé ruce, nějak prapodivně hranaté, a pak se jí z levé ruky vyřinulo jasné světlo. Teď už bylo jasně vidět, že je to muž a že nemá hranatou ruku, jen na ní má zbroj, která svítí.

Muž se rozhlédl, spatřil Gaia a přiložil si prst na ústa. Jako by Gaia napadlo, že by mohl vydat nějaký zvuk. Teprve teď si všiml, že ve druhé ruce má muž masivní pánev.

Položil ji na pracovní stůl, popadl pár nástrojů a urazil jí držadlo. Pak chvíli něco kutil, sbalil si věci a chystal se asi k odchodu. Ještě se ale jednou ohlédl po zkoprnělém Gaiovi, něco zamumlal nějakou nesrozumitelnou řečí, popadl ze stojanu štít a kopí, a pak s lupnutím a modrým zábleskem zase zmizel.

Gaia konečně začaly poslouchat nohy a v děsu vyběhl z postele a nezastavil se, než doběhl do stanu Rufuse, jeho známého písaře. Chtěl si totiž nechat zapsat to, co slyšel, dokud si to pamatuje.

Teoretická úloha28-3-2 Líný písař (9 bodů)

Písař se pokouší zapsat vzkaz, který mu Gaius Fabius diktuje. Ten si však není příliš jistý tím, co slyšel. U každé věty si třeba pamatuje, že zněla trochu jako jedna věta, trochu jako jiná.

Písař by chtěl zapsat raději všechno, ale zase se při psaní nechce moc nadřít. Gaius nadiktuje písaři obě možné věty a písař chce najít co nejkratší větu (řetězec), kterou je možno vyškrtáním nějakých písmen převést na obě Gaiovy věty.

Příklad: Třeba pro věty (řetězce) mujstit a mojesin je řetězec muojestitn jedním z možných nejkratších řetězců obsahujících obě věty. Věty se z něj dají získat třeba takto:

muojestitn
mu_j_stit_
m_ojes_i_n

Řešení

Ráno to ale bylo ještě horší…

„Kde je moje zbroj? Tak kde?!?“

Gaius si pomyslel, že centurion vypadá dnes obzvláště naštvaně. Bohužel měl centurion ve zvyku posílat lidi, co ho naštvali, na nějaké speciální úkoly. Nemělo smysl pokoušet se mu vysvětlovat, že tu v noci byl nějaký divný cizinec, kterého neviděly hlídky, který mluvil divnou řečí, kterému svítila ruka a který shodou náhod ukradl centurionovu zbroj, kterou měl Gaius vyleštit. To prostě nemělo cenu.

Tak se Gaius smířil s tím, že bude muset někde v hlubinách zásobovací sítě legie sehnat zbroj novou, jinak že se prý nedožije dalšího rána. Bohužel sehnat novou zbroj pro centuriona nebylo tak jednoduché, vrchní zbrojíř se totiž vyžíval v neskutečné byrokracii.

Teoretická úloha28-3-3 Formulář na zbroj (10 bodů)

K sehnání zbroje je potřeba vyplnit spoustu formulářů. Každý formulář se dá vyplnit dvěma způsoby, a to kladně a záporně, a má navíc své číslo. Gaius má zmapováno, kdo a jak v táboře legie vydává formuláře.

Platí, že každý formulář vydává nejvýše jeden člověk. Někteří lidé v táboře své formuláře přímo vydají bez potřeby nečeho dalšího, ale ostatním je nutné nejdříve ukázat jiné již vyplněné formuláře, a teprve na jejich základě vydají svůj formulář (buď kladně, nebo záporně vyplněný).

To, jak vyplněný formulář vydají, je totiž dáno logickou funkcí (and, or, xor nebo not) na formulářích, které dostanou k nahlédnutí.

Lidi v táboře máme očíslované a dostáváme popis byrokratické struktury v táboře zadaný jako:

Zajímalo by nás, které všechny formuláře a jak ohodnocené umíme získat (předpokládejte, že formulář je vydán jen a pouze tehdy, pokud ukážeme všechny formuláře, na nichž závisí – tedy nestačí třeba pro formulář vydávaný podmínkou Fa and Fb donést pouze negativní Fa s tím, že již určuje výsledek).

Řešení

Nakonec se Gaiovi povedlo sehnat novou zbroj až odpoledne. Doufal, že si pak konečně odpočine, ale o tom si mohl nechat leda tak zdát. Legie se chystala na střet s barbarskou armádou, a tak si legát svolal všechny starší legionáře starající se o obléhací stroje.

Jeho plánem bylo vyvážit početní převahu barbarů lepší disciplínou legionářů, lepší výzbrojí a také použitím katapultů. Vybrané centurie měly v rozsáhlém údolí zaujmout pevné pozice a katapulty ostřelovat blížící se barbary.

No a rozmístění katapultů byl právě úkol pro legionáře starající se o obléhací stroje.

Teoretická úloha28-3-4 Katapulty (11 bodů)

Legát chce nechat po údolí rozděleném do čtvercové sítě N×N rozmístit K katapultů. Rozkázal, že každý katapult smí střílet jen rovnoběžně s čtvercovou sítí (tedy podle políček horizontálně nebo vertikálně, ne však našikmo) a chce, aby se katapulty vzájemně neohrožovaly (nebyly žádné dva ve stejném sloupci nebo řádku).

Údolí je ale trochu podmáčené, a tak máme pro každý katapult určený obdélník, ve kterém může stát.

Pro zadané N, K a pro určené obdélníky pro každý katapult najděte rozmístění katapultů tak, aby se vzájemně neohrožovaly, nebo rozhodněte, že takové rozmístění neexistuje.

Lehčí variantaLehčí varianta (za 5 bodů): Řešte úlohu v jednorozměrné variantě: Pro každý katapult máme daný úsek, kde může stát, a nesmí stát dva na stejném políčku.

Řešení

Další ráno část legie vyrazila. V táboře zůstalo dvacet centurií, zbylých čtyřicet odvedl legát do boje. Průzkumníci nelhali, skutečně se jim povedlo zaujmout výhodné postavení v širokém údolí a proti rozptýleným barbarům fungovala legátova rozptýlená taktika překvapivě dobře.

Osamocení barbaři se tříštili o pevně stojící hradbu štítů, větší skupinky padaly za oběť přesně mířeným zásahům košů s kamením z katapultů.

Gaius ale řešil problém se svým katapultem. Po každém výstřelu se v nestabilní půdě pohnul, sklouznul rohem do tůňky vedle a bylo potřeba ho zase vytáhnout a správně nasměrovat. To velmi snižovalo rychlost palby.

Pomocníkům se povedlo sehnat spoustu dřevěných fošen a Gaius je chtěl použít k zatížení katapultu, aby se nehýbal. Uprostřed několika desítek legionářů, kteří stáli kolem dokola v neproniknutelné hradbě, začal fošny osekávat a svazovat k sobě.

Praktická opendata úloha28-3-5 Závaží z fošen (8 bodů)

Máme několik silných dřevěných fošen. Všechny jsou stejně tlusté, ale liší se svými rozměry. Chtěli bychom z nich sestavit co možná nejtěžší závaží, neboli závaží s největším objemem, protože všechny fošny jsou ze stejně těžkého dřeva. Prkno o rozměrech 1×1 váží 1 jednotku.

Aby se nám ale závaží nerozpadalo, musí mít všechny vrstvy na sobě stejný rozměr. Jednotlivé fošny můžeme oříznout (rovnoběžně s jejich hranami a s tím, že odřezky zahazujeme), můžeme je otočit (prohodit šířku a výšku), nebo dokonce nepoužít vůbec. Nemůžeme však mít v závaží nějakou fošnu menší (ať už šířkou nebo výškou) než jinou.

Formát vstupu: Na prvním řádku vstupu obdržíte počet fošen, na dalších N řádcích pak rozměry každé fošny jako dvě čísla oddělená mezerou.

Formát výstupu: Na výstup vypište jediné číslo – maximální váhu závaží, kterou jsme schopni ze zadaných fošen poskládat.

Ukázkový vstup: 
6
5 11
1 1
5 6
1 2
6 4
4 6
Ukázkový výstup: 
96

Druhou a čtvrtou fošnu nepoužijeme vůbec, ostatní ořízneme na rozměry 6×4, což nám dohromady dá objem (a tedy i váhu) 96.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Řešení

Nadšení z toho, že se povedlo katapult stabilizovat, však netrvalo dlouho. Vlastně trvalo docela krátce, protože barbarů najednou bylo příliš mnoho a legionáři začínali být vysílení. Ze svého vyvýšeného postavení Gaius viděl, jak hradby štítů několika centurií zakolísaly, barbaři se dostali skrz a jednotlivé legionáře svým počtem udolali. Takhle nemůžeme vydržet moc dlouho, pomyslel si Gaius.

Navíc začala padat tma a situace se stávala ještě nepřehlednější a prohra stále zřejmější. Asi si to uvědomil i legát a vzduchem se ke všem zbývajícím vojákům doneslo troubení signálu k ústupu.

Katapulty byly opuštěny a jednotlivé centurie se začaly v želvích formacích (a želvím tempem) sunout k jižní části údolí, odkud přišli.

Než se zbývající legionáři shromáždili do jedné skupiny, zbyla z legie sotva polovina. Nikdo nevěděl, kolik jejich druhů je mrtvých, kolik padlo do zajetí (pokud barbaři vůbec brali zajatce) a kolik se jich ztratilo.

Aby se zjistilo, kolik jich z každé centurie zbylo, poslal každý centurion mezi svými muži helmici. Každý, kdo přežil, do ní měl vhodit kamínek. A aby se jednotlivé centurie nepomíchaly, každý měl předat helmici jenom někomu, koho zná.

Teoretická úloha28-3-6 Počítání přeživších (12 bodů)

Přeživší legionáři se potřebují spočítat. Dělají to tak, že si mezi sebou posílají helmici a vkládají do ní kamínky. Helmice by měla obejít všechny legionáře a to tak, že u každého se objeví právě jednou.

Legionáři jsou ochotní helmici předat někomu, koho znají osobně, někomu, koho zná někdo koho znají, nebo někomu, koho zná někdo koho zná někdo koho znají. Zkráceně řečeno jsou ochotni předávat helmici jen někomu, kdo je od nich maximálně tři přátelství daleko (A předá helmici D, pokud se znají A-B, B-C a C-D). Známosti jsou symetrické, tj. pokud A zná B, tak i B zná A.

Pro skupinu legionářů a neorientovaný graf toho, jak se znají, najděte takovou posloupnost předávání helmice, aby respektovala podmínku výše, každý legionář dostal helmici do rukou právě jednou a helmice se dostala zpátky do rukou centurionovi.

Lehčí variantaLehčí varianta (za 6 bodů): Vyřešte úlohu, pokud víte, že graf známostí mezi legionáři je strom.

Řešení

Když zjistili, kolik jich je, rozhodlo se, že se legie stáhne nazpět do opevněného tábora. Protože byla noc, utvořili velkou formaci ve tvaru kruhu ježící se kopími na všechny strany a v ní opatrně postupovali zpátky.

Útoky barbarů ustaly, ale o to byla noc zlověstnější. Kruhová formace se přiblížila k řídkému lesu v soutěsce a zastavila se. Legát tu cítil nějakou léčku, stromy byly vysoké a košaté, tak košaté, že se na každém z nich mohla skrývat spousta barbarů.

Podrobnou mapu lesa dodali průzkumníci už minulý den a legát by teď potřeboval vědět, jestli může legii lesem bezpečně provést, nebo musí les někudy obejít.

Praktická CodExová úloha28-3-7 Legie v lese (13 bodů)

Máme legionáře v kruhové formaci s poloměrem r. Dále máme také podrobnou mapu lesa. Les na obou stranách svírá soutěska a stromy jsou vzhledem k velikosti legie tak malé, že jejich kmeny můžeme považovat pouze za body.

Legie chce projít od severu na jih lesa a to tak, aby se cestou vyhnula všem stromům (protože na nich mohou číhat barbaři). Do kruhu představujícího legii se tedy během postupu lesem nesmí dostat žádný strom a ani nesmí kruh zasahovat za některou z bočních hranic (protože les je v soutěsce).

Pro zadaný les rozhodněte, jestli taková cesta skrz les existuje, nebo ne.

Tato úloha je praktická a řeší se ve vyhodnocovacím systému CodEx. Přesný formát vstupu a výstupu, povolené jazyky a další technické informace jsou uvedeny v CodExu přímo u úlohy.

Řešení

Stalo se, to co legát očekával – legii v lese přepadli barbaři. Díky legátově prozíravosti sice neseskákali ze stromů přímo do středu legionářů, ale stejně se strhla bitva za světla měsíce a několika málo pochodní.

Kruh z legionářů se během boje přeléval a deformoval, ale držel. Vždy, když byli legionáři donuceni o pár metrů ustoupit, přišli další spolubojovníci a barbary zase vytlačili dál. Bohužel Gaius se při jednom z těhle výpadů ocitl mimo ochranný kruh štítů. Jediné štěstí bylo, že si ho nikdo z barbarů nevšiml, a tak se mu povedlo se rychle odkulit do nějaké jeskyně.

Teď ale sledoval, jak se od něj hradba štítů postupně vzdaluje a mezi ním a jeho druhy pobíhá mnoho barbarů. Bez meče nebo alespoň štítu se tam nemá šanci dostat! Ještě, že si ho zatím v té jeskyni nevšimli…

Jeho přemýšlení přerušil divný zvuk za jeho zády. Rychle se otočil a málem vykřikl. Opět se tu objevil ten tajemný cizinec, kterému po těle běhali postupně mizející modří hadi, v ruce nesl pochodeň. Také ho do nosu udeřil odporný zápach spáleného masa a všiml si, že na zem před cizincem dopadla zuhelnatělá lidská paže.

Cizinec vypadal sám docela zaskočený, ale rychle se vzpamatoval a s nějakým zamumláním odkopl spálenou ruku dále od sebe. Pak se rozhlédl, vytáhl zpoza pasu nějakou svítící krabičku a začal s ní obcházet stěny. O Gaia se nezajímal.

Po chvíli asi objevil to, co hledal, udeřil do stěny jeskyně kladivem, odloupl nějaký divný kus kamene, sáhl po svojí levé ruce a se zablesknutím zmizel.

Než se však Gaius stihl vzpamatovat a pořádně nadechnout, zablesklo se podruhé a cizinec se vrátil. Teď tam však místo pochodně stál s pánví v jedné ruce a centurionskou zbrojí ve druhé. Řekl něco dalšího nesrozumitelného a hodil zbroj i s mečem Gaiovi k nohám. Pak ho rukou pobídl, aby se do ní navlékl.

Gaius dlouze neváhal a cizince poslechl. Jakmile na sebe zbroj navěsil, podíval se na cizince, co teď. Ten se nahnul, hodil něco nalevo do lesa, na prstech odpočítal od tří do jedné a silně strčil Gaia do zad. Ten vyběhl současně s tím, co se zleva z lesa začaly ozývat divné zvuky.

Díky téhle diverzi se dostal zhruba do poloviny vzdálenosti k postupující legii, než si ho všimli barbaři. A pak přišel ke slovu meč, štít a zbroj. Z posledních sil se probojoval zpátky ke svým druhům a tak se stalo, že Gaia zachránil neznámý cizinec.

Příběh pro vás vyprávěl

Jirka Setnička

Seriálová úloha28-3-8 Inteligence hejna (15 bodů)

V tomto díle se budeme naposled věnovat evolučním algoritmům a oproti minulému dílu budeme opět více čerpat inspiraci z chování přírody. Konkrétně si budeme všímat struktur chování skupin živočichů. Tyto algoritmy patří do kategorie, která se souhrně nazývá Inteligence hejna.

Co ale znamená samotný pojem inteligence hejna? V přírodě existuje řada živočichů, jejichž jedinci se chovají velmi jednoduše a řídí se jen následováním pár jednoduchých pravidel. Takoví jedinci obvykle nemají potenciál samotní přežít, a nebo dokázat velké věci. Když ale vezmeme celé hejno takových jedinců, kteří všichni usilují o stejnou věc, tak tím získáme něco velkého.

Například si představme mravence, který se snaží postavit své obydlí. Ten musí jít pro dřívko, odložit jej na hromadu, pak jít pro další, opět jej položit a tak dál. To vypadá jako jednoduchý úkol. Akorát jeden mravenec tyto dřívka nedokáže shánět dost rychle. Než donese druhé, tak mu první dřívko může sebrat jiný živočich, odfouknout vítr, a nebo se nám mraveneček může polámat. V každém případě tento jeden mravenec má jen pramalé šance na úspěšné dostavení celého obydlí.

Nyní si znova představme stejnou situaci, ale namísto jednoho mravence bude obydlí stavět milion mravenců, kteří všichni chtějí postavit společné obydlí. Tato situace je mnohem nadějnější. Obydlí sice musí postavit řádově větší, ale také jim práce půjde řádově rychleji a z nasbíraných dřívek se nám rychle stane hromádka. A když se náhodou jednomu mravenci něco stane, tak tam pořád máme statisíce dalších, kteří jej mohou nahradit.

Co z toho plyne pro informatiku? Máme jedince, kteří se chovají jednoduše. Ty zvládneme snadno simulovat pomocí sady jednoduchých pravidel. Když pak vezmeme hodně takových jednoduchých jedinců a budeme je simulovat všechny najednou v jednom prostředí (tak, aby se navzájem ovlivňovali), tak nám dohromady vytvoří složitou strukturu chování, kterou už nejspíš nedokážeme jednoduše popsat.

Z informatického pohledu zbývá jen jedno. Navrhnout takové chování jedinců, jejich cíle a takové prostředí, aby nám celé takové hejno vyřešilo zadaný problém. My pro chování jedinců budeme hledat inspiraci ve skutečných příkladech. Nepovede se nám dosáhnout toho, že najdeme tak skvělého živočicha, jehož simulací dokážeme vyřešit všechny problémy, ale uvidíme, že inspirace konkrétním živočichem nás dovede ke ke konkrétní třídě problémů, na které se simulace zrovna tohoto živočicha hodí.

Chování mravenčí kolonie

Mravenci jsou sociální hmyz, který žije ve skupinách velkých 2 až 25 milionů jedinců. My si budeme všímat, jak se chovají při shánění potravy. Mravenci začnou víceméně náhodně prohledávat okolí mraveniště a hledat potravu. Jakmile je některý z nich úspěšný, tak po své cestě vypouští feromony, jimiž dává ostatním mravencům najevo, že tato cesta je dobrá. Ostatní mravenci jsou pak schopni tyto feromony cítit a automaticky preferují cesty s vyšší koncentrací feromonů. Tomuto se říká mechanizmus pozitivní odezvy.

Je důležité si uvědomit, že tam nikde není žádný centrální mravenec, který by pohyb řídil, a že celé shánění potravy vyplyne na povrch automaticky z náhodného chození a za pomoci feromonů. Cesty k potravě postupně sílí a jakmile tam potrava dojde, tak mravenci přestanou produkovat feromony, ty začnou postupně vyprchávat a mravenci si najdou jinou cestu k další potravě.

Celá kolonie se tedy umí samoorganizovat bez jakékoliv centrální či vnější pomoci za využití produkování feromonů. Ty v prostředí pak fungují jako sdílená krátko/dlouhodobá paměť všech mravenců z mraveniště.

Optimalizace mravenčích kolonií

Hledání potravy mravenců budeme simulovat jako hledání cesty v grafu. Máme zadaný ohodnocený graf G = (V, E), ve kterém bychom chtěli najít co nejkratší cestu z vrcholu s (mraveniště) do vrcholu t (potrava). My si popíšeme základní mravenčí algoritmus (Ant System), ze kterého pak vychází drtivá většina ostatních mravenčích algoritmů.

Každá hrana ij má svou délku dij a intenzitu feromonů fij. Mravenec začne ve vrcholu s a vydá se po grafu až dokud nedojde do t (případně nepřekročí maximální počet kroků). Pokud stojí ve vrcholu i, tak v dalším kroce přejde do vrcholu j s pravděpodobností

kde bij = 1/dij je „vhodnost hrany“ – čím kratší, tím vhodnější, a α, β jsou parametry ovlivňující význam obou složek. Obvykle se α, β volí kolem 2.

Intenzita feromonů se na začátku výpočtu může zvolit třeba 1 či menší konstanta, nebo bij či úplné jinak. Záleží, jak nám to pro konkrétní algoritmus vyhovuje. Volbou fij = bij obvykle nic nezkazíme.

Jedna iterace algoritmu má tři fáze:

  1. Vytváření řešení (mravenci hledají cestu)
  2. Aktualizace feromonů (vypařování a zvyšování mravenci)
  3. Vnější zásahy (nepovinná část)

Vytváření řešení jsme si již popsali. To jen mravenci na základě aktuálních pravděpodobností hledají cestu v grafu. Pak se odpaří intenzita feromonů na všech hranách podle

fij = (1 - ρ) · fij

kde ρ∈[0, 1] je intenzita odpařování. Čím vyšší ρ, tím více se feromony odpařují. Po odpaření pak všichni mravenci znova projdou své cesty a intenzitu feromonů každé hrany ij na nich zvýší o 1/L, kde L je délka nalezené cesty. Případně o rozumný násobek této hodnoty či dle jiné klesající funkce závisející na délce hledané cesty.

fij = fij + 1/L

Vnější zásahy jsou nepovinná část algoritmu. Jedná se o vylepšení, která se nedají udělat z pohledu mravence. Obvykle se jedná o různé zvýhodňování nejlepších mravenců, podrobnější hledání v okolí nejlepšího řešení a podobně.

Tím jsme popsali celý základní mravenčí algoritmus a nyní se podíváme na jeho aplikaci na reálný problém.

Aplikace v problému obchodního cestujícího

Zadání problému: Máme zadaný seznam n měst a vzdálenost každé dvojice z nich (tedy úplný graf o n vrcholech). Obchodní cestující by všechny tyto města chtěl navštívit (každé právě jednou) a vrátit se do toho, kde začal. V jakém pořadí je má projít?

Toto je slavný problém, pro který není znám žádný algoritmus, který by jej efektivně řešil. Tak nám nezbývá než se jej snažit vyřešit optimalizačně. Jelikož v problému hledáme nějakou cestu v grafu, tak se nabízí použít mravence.

Nalezení potravy v tomto případě bude znamenat projití všech vrcholů grafu, každým právě jednou. Čím kratší cestu najdeme, tím více feromonů budeme vydávat. Jelikož se pohybujeme na úplném grafu, tak hledání takových cest nebude velký problém.

Jeden mravenec vždy začne v náhodném vrcholu a na základě feromonů přejde do dalšího vrcholu. Vždy ale bere v úvahu jen ty sousedy, které ještě při své cestě nenavštívil. Takže mravenec pokaždé nějakou cestu nalezne a ta bude procházet právě přes právě n vrcholů. Čímž jsme v ještě lepší situaci než při hledání nejkratší cesty, kde nám mravenci mohli i zabloudit.

Zbytek mravenčího algoritmu zůstává naprosto stejný.

Úkol 1 [15b]

Řešte problém obchodního cestujícího na obcích České Republiky. Data si můžete stáhnout na obvyklém místě na stránce seriálu.

Ve vstupním souboru najdete na každém řádku (je jich 6 251) popis jednoho města formou následujících údajů. Počet obyvatel obce, x-ová souřadnice obce, y-ová souřadnice obce a název obce. Jednotlivé údaje jsou oddělené mezerou. Za poskytnutí dat, která by měla být platná k začátku roku 2011, děkujeme ČSÚ – https://www.czso.cz/.

Pro jednoduchost vzdálenost mezi dvěma městy uvažujeme jako vzdálenost bodů v rovině. Úlohu řešte pro všechna města. Takový graf, ale pro první zkoušení algoritmu možná bude příliš velký, tak úlohu můžete zkusit řešit pro obce s více jak 2 500 obyvateli, případně pro obce s více jak 10 000 obyvateli.

Pro řešení můžete použít jak algoritmus mravenců, tak jakýkoliv jiný postup. Porovnejte výsledky, kterých jste jednotlivými postupy dosáhli.

Možné modifikace mravenčí kolonie

Elitářská strategie: Preferování doposud nejlepší cesty za celý dosavadní průběh algoritmu. Funguje tak, že si pamatujeme doposud nejkratší cestu a v každé iteraci během aktualizace intenzity feromonů přičteme ε/Lb ke všem hranám této cesty, kde ε určuje sílu vlivu nejlepší cesty a Lb je její délka.

Vliv pořadí: Lepší mravenci budou produkovat ještě více feromonů než ti horší. Mravence seřadíme podle délky jejich cesty a feromony produkuje jen w nejlepších z nich. r-tý mravenec produkuje feromony podle

fij = fij + (w-r+1)/L

Další inteligence hejna

Existuje ještě řada dalších modifikací algoritmu mravenčí kolonie. Ty ale v tomto seriálu nezvládneme pokrýt. Raději si uděláme rychlý přehled dalších inspirací hejn, které v přírodě můžeme najít.

Optimalizace hejnem částic

Anglicky Particle Swarm Optimization je trochu podobné diferenciální evoluci z minulého dílu. Hejno sestává z jednotlivých částic, které se pohybují v prohledávacím prostoru. Každá má svou aktuální polohu a vektor rychlosti. Rychlost se pak stáčí k doposud nejlepšímu nalezenému bodu dané částice a nejlepší nalezené poloze všech částic.

Optimalizace včelím rojem

Zahrnuje celou skupinu algoritmů, které hledají inspiraci v rojích včel. Jedinci v algoritmu jsou obvykle rozděleny do několika skupin včel, kde každá hraje svou specifickou roli. Algoritmy nachází uplatnění jak při řešení reálných optimalizací, tak při řešení diskrétních problémů.

Například můžeme mít tři typy včel: dělnice, pozorovatelky a průzkumnice. Nejdříve dělnice vyletí do prostoru řešení a pomocí včelího tanečku dávají vědět pozorovatelkám, jak je jejich řešení dobré. Pozorovatelky z nich pomocí vážené pravděpodobnosti vyberou ty, které jsou úspěšné. Dělnice, které ve svém okolí dlouho nebyli úspěšné se pak změní na průzkumnice a vydají se zkoumat jinou oblast prostoru řešení.

Optimalizace hejnem světlušek

Každá světluška má svou svítivost v závislosti na její úspěšnosti. Čím úspěšnější, tím více září a přitahuje ke své pozici ostatní světlušky. Každá světluška má také omezenou vzdálenost, kam až dohlédne.

Karel Tesař

Řešení