Čtvrtá série dvacátého osmého ročníku KSP
Celý leták v PDF.
- Odměna série: Čokoládu pošleme každému, kdo z úloh této série získá alespoň 42 bodů.
Zadání úloh
Příběh pěti domů
Utahuji poslední šroub, ještě pro jistotu naposled změřím napětí, balím si
nářadí a vyrážím zpátky domů. Už se tu nechci zdržovat ani minutu. Je pátek po
deváté večer a mě ještě doma čekají přípravy na víkend a taky jsem dětem
slíbil pohádku.
Pracuji jako technik pro jednu telefonní společnost. Práce to není špatná,
docela mě i baví a hlavně mě v běžném životě příliš nezatěžuje. Akorát když
v mém okruhu nastane náhlý výpadek, jako třeba teď, tak to musím hned jít
opravit. Ale co nadělám, aspoň že se to tentokrát stalo přímo v našem bloku,
tak jen stačí projít ulicí a jsem doma.
 28-4-1 Sledování telefonů (9 bodů)
28-4-1 Sledování telefonů (9 bodů)
V ulici stojí v řadě N domů. Každý z nich má jeden telefon a je
propojen telefonní linkou s dvěma sousedními domy (jedním v případě krajních).
Grafově řečeno tvoří telefonní síť cestu: vrcholy představují domy a hrany
spoje. Pokud zavoláme z domu a do b, musí hovor projít přes všechny spoje
ležící na cestě mezi a a b.
U každého spoje víme, kolik přes něj za poslední týden prošlo hovorů. Na základě
této informace bychom chtěli zjistit, kdo komu volal. To samozřejmě nelze určit
jednoznačně, stejný provoz na spojích může vytvořit mnoho různých řešení.
Vyberte to s nejmenším celkovým počtem hovorů (pokud je více takových, libovolné
z nich).
Například pro N=7 a počty hovorů na spojích postupně 1,3,2,1,3,2 muselo
proběhnout nejméně pět hovorů a mohly vypadat například takto:
Tedy proběhly hovory A → D, B → C, B → F a E → G
a znovu E → G.
S menším počtem hovorů nelze vytvořit zadané vytížení linek.
 Lehčí varianta (za 5 bodů): Řešte za předpokladu, že se počty zachycených hovorů
na libovolných dvou sousedních spojích liší maximálně o 10.
Lehčí varianta (za 5 bodů): Řešte za předpokladu, že se počty zachycených hovorů
na libovolných dvou sousedních spojích liší maximálně o 10.
Řešení
V mé ulici stojí pět domů a při takové večerní procházce si aspoň zas jednou
udělám obrázek, jak se daří sousedům. Všichni zde žijeme už téměř deset let
a k našemu nastěhování se váže společný příběh.
* * *
Bylo mi tehdy 25 let a o tomto roce můžu jednoznačně mluvit jako o roce smůly.
Firma, ve které jsem byl zaměstnán, prodělávala, a tak musela čistit. Jako
nezkušený mladík jsem to odnesl já a další práci dlouho nemohl sehnat. A aby
toho nebylo málo, tak mi navíc o pár týdnů později vykradli byt a stopy
zakryli tím, že ho prostě zapálili. Pachatele se dopadnout nepodařilo,
vchodové kamery nikoho nezaznamenaly a ani nebyly patrné jakékoliv známky
vniknutí. Prostě záhada a pojištěný jsem nebyl. Takže jsem najednou neměl ani
práci, ani kde bydlet, a nápad, jak z toho ven, už vůbec ne.
Večer, když jsem svůj žal zapíjel v místním lokále, neměl jsem totiž kam jinam
jít, si ke mně přisedl uhlazený muž v obleku a začal se vyptávat, co mě trápí.
Stručně jsem mu popsal svou situaci, svěsil hlavu a zhrzele seděl dál. Opravdu
jsem neměl náladu se s někým vykecávat.
Muž si na papír načmáral pár poznámek a pak povídal: „Pracuji pro společnost
jménem Druhá šance a mám pro vás nabídku. S kolegy zrovna zakládáme nový
projekt a vy byste pro nás byl ideální kandidát. Vaší účastí byste vyřešil
všechny problémy s prací a bydlením, které vás momentálně sužují. Rozhodnutí
je teď na vás. Pokud byste měl zájem se dozvědět více, zavolejte na toto číslo
a domluvíme si schůzku. Moc ale neváhejte, naše prostředky jsou omezené
a mohli bychom místo vás sehnat někoho jiného.“
Předal mi svou vizitku, rozloučil se a s úsměvem odešel. O nabídce jsem dlouze
nepřemýšlel a hned ráno jsem volal, že přijímám. Schůzka byla další pondělí.
Přišel jsem na zadanou adresu a byl usazen do čekárny. Bylo nás tam celkem
pět, tři muži a dvě ženy. Na pohled jsme všichni byli ve věku kolem
pětadvaceti let. Z kanceláře vyšel muž, kterého jsem již znal, v ruce držel
nějaké papíry a povídal: „Výborně! Tak jste tu všichni. Vybrali jsme do
našeho projektu právě vás pět, protože si myslíme, že jste poslední dobou
v životě neměli štěstí a potřebujete dostat svou »druhou šanci«. Tu vám
můžeme nabídnout. Já si teď ještě rychle musím něco dopřipravit. Zatím si
projděte a podepište tyto dokumenty a trochu se seznamte.“
 28-4-2 Podepisování dokumentů (8 bodů)
28-4-2 Podepisování dokumentů (8 bodů)
V kruhu sedí N lidí, kterým potřebujeme předat dokumenty k podepsání.
O každém víme přesně, jak dlouho mu bude trvat, než dokumenty zvládne projít.
K dispozici máme dvě sady dokumentů, které dáme dvěma lidem, kteří v kruhu
sedí vedle sebe. Ti pak dokumenty pošlou dále po kruhu. Navrhněte algoritmus,
který zjistí, kterým dvěma sousedům dokumenty podat, aby celkový čas procházení
dokumentů všech lidí byl co nejmenší.
Například pro následující skupinku (čísla udávají dobu prohlížení v minutách):
je jedno z možných řešení naznačené šipkami (dokumenty dáme na začátku osobám
s časy 6 a 9). Celkový čas bude 14 minut. Rozmyslete si, že lépe to nejde.
Řešení
První žena byla bruneta oblečená v červených šatech a botách na vysokých
podpatcích. Svou image měla doplněnou o černý módní klobouk, zlaté náušnice
a náhrdélník. Nebyla vyloženě krásná, ale jak se takto vyšvihla, tak se
rozhodně bylo na co koukat. Manžel se s ní prý rozvedl, protože dle jeho
názoru zbytečně utrácela za nesmysly a sama toho moc nevydělala. Nakonec
zmínila, že její manžel stejně byl jen takový blbeček, který ji nedokázal
docenit, že si ji ani nezasloužil a že si určitě brzy najde lepšího.
Druhým byl pohublý muž, který pořád něco ťukal do tabletu a moc se s námi
nechtěl bavit. Pracovával jako programátor, pak se ale nepohodl s nadřízenými,
když chtěl všechny pracovní dny využívat home office a komunikovat pouze po
chatu. S rodiči si také nerozumněl. Neměli totiž pochopení pro hraní online
počítačových her a stravování pomocí objednávek přes internet. Prostě takový
ajťák.
Třetí osobou byla rozcuchaná potetovaná slečna, oblečená v hipsterském stylu
a vlasy obarvenými na tmavě zelenou. Dle svých slov žije pohodový život, ve
kterém jí toho moc nechybí. Stálou práci nemá, ale když potřebuje, dopomáhá si
brigádami, většinou roznášením letáků. Od rodičů odešla v sedmnácti, protože
prý měli příliš oldschoolový pohled na svět a zbytečně ji omezovali. Sedí tu
s námi, protože dostala nabídku a nové příležitosti neodmítá.
Čtvrtým přítomným byl muž, takový trochu podivín. Měl vystudovaná práva,
sociologii a nyní začal chodit na ekonomku. V životě se dostal do slepé
uličky, když přesáhl věk dvaceti šesti let a za svá studia musel začít platit.
Neměl totiž z čeho. Navíc to byl vitarián, což také nevycházelo nejlevněji. Ve
svém životě dodržoval přísná pravidla ohledně stravování, denního režimu,
spánkového režimu a tak vůbec.
Pátý jsem byl já, muž s vyhořelým bytem, bez práce a s nulovou představou, jak
tuto zoufalou situaci řešit. Jinak ale obyčejný chlap s ne příliš náročnou
představou o životě. Chtěl jsem hlavně založit rodinu, o tu se postarat, najít
si pár přátel a s těmi občas něco podniknout či v zimě vyjet na hory. Hlavně
aby bylo pořád co dělat a za čím jít.
Po vyslechnutí příběhů všech přítomných bylo naprosto zjevné, že jsme všichni
navzájem diametrálně odlišní a máme naprosto jinak seřazené své životní
hodnoty.
 28-4-3 Řazení životních hodnot (10 bodů)
28-4-3 Řazení životních hodnot (10 bodů)
Máme zadanou množinu X s N navzájem různými celými čísly
a posloupnost R1, … , RN-1 operátorů menší než (<) a větší než (>).
Najděte uspořádání x1, … , xN čísel z množiny X takové, aby platilo
x1 R1 x2 R2 ...RN-1 xN.
Formát vstupu:
Na prvním řádku dostanete číslo N. Na druhém řádku najdete N čísel tvořících množinu X (v neurčeném pořadí)
a na třetím N-1 znaků < nebo > bez mezer.
Formát výstupu:
Jeden řádek obsahující čísla z X v takovém pořadí, že splňují zadané
relace. Správných řešení může být víc, vypište libovolné z nich.
Ukázkový vstup:
6
42 2 3 8 1 5
>><><
Ukázkový výstup:
8 5 2 3 1 42
Výstup je správný, protože platí: 8>5>2<3>1<42.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Po chvíli z kanceláře znova vyšel ulízlý muž v obleku. Vybral od nás podepsané
dokumenty a povídal: „Jmenuji se Dalimír a mým úkolem je uvést vás do
celého projektu a postarat se o všechny formality s ním spojené. Všem pěti
z vás nějakým způsobem pomůžeme vyřešit váš aktuální problém s bydlením
a financemi…“
„Heeej! Já nemám žádnej problém a určitě nepotřebuju ničí pomoc!“ ozvala se
zelenovlasá hipsterka.
Dalimír ale pokračoval dál, jako by ji vůbec neslyšel: „Na kraji města
v ulici Nádvorní jsme postavili pět domů a každý z nich se chystáme darovat
jednomu z vás spolu ještě s dalšími výhodami. Jste připraveni se na ně jít
podívat?“
Nezmohl jsem se ani na slovo. Tak úžasnou zprávu jsem vůbec nečekal. Ostatní
na tom byli podobně. Vyhublý ajťák dokonce na chvíli přestal koukat do tabletu
a dámě v klobouku v obličeji na okamžik zableskl výraz pokory a vděku.
Po chvíli ticha se ozval věčný student: „A nebudeme mít pak problémy se
zdaněním? Prošly ty domy oficiální kolaudací? A je legální v nich už bydlet?“
„Nebojte, o to vše jsme se postarali,“ uklidňoval jej Dalimír.
„Tak vyrazíme!“ pokračoval.
Dojeli jsme na místo a začali procházet ulicí. Dalimír nám vše pečlivě
popisoval. Kde najdeme zastávky, kterým směrem je nejbližší obchod, a tak
podobně. Až jsme došli k prvnímu, obrovskému domu.
„Nyní mi dovolte, abych vám představil první dům. Jedná se o tuto vilu se
zahradou, bazénem a dvěma garážemi! Garáž samozřejmě není prázdná, ale najdete
v ní nejnovější model auta Subaru XV Crosstrek. Samotný dům se pyšní dvěma
kuchyněmi, třemi koupelnami a ložnice pro hosty je samozřejmostí. Interiér je
navíc zkrášlen řadou obrazů historického i moderního umění…“ představoval
Dalimír.
 28-4-4 Podivuhodný obraz (12 bodů)
28-4-4 Podivuhodný obraz (12 bodů)
 V domě visí podivuhodný obraz. Je na něm nakreslených N bodů, které jsou
spojeny dohromady M čarami. Celý obraz je černo-červený a má zajímavou
vlastnost. Pokud z bodu vedou alespoň 2 čáry, některá z nich je černá
a některá červená.
V domě visí podivuhodný obraz. Je na něm nakreslených N bodů, které jsou
spojeny dohromady M čarami. Celý obraz je černo-červený a má zajímavou
vlastnost. Pokud z bodu vedou alespoň 2 čáry, některá z nich je černá
a některá červená.
Co kdyby ale obraz vypadal jinak? Šel by pořád takto nakreslit? Vymyslete
algoritmus, který na vstupu dostane neorientovaný graf a obarví jeho hrany
dvěma barvami tak, že každý vrchol se dotýká hran obou barev (případně
zjistěte, že to nejde). Pozor, vstupní graf nemusí být souvislý.
 Lehčí varianta (za 8 bodů): Řešte za předpokladu, že všechny vrcholy mají sudé stupně.
Lehčí varianta (za 8 bodů): Řešte za předpokladu, že všechny vrcholy mají sudé stupně.
Formát vstupu:
Na prvním řádku dostanete dvě celá čísla N a M udávající počet vrcholů
a hran. Každý z následujících řádků popisuje jednu hranu pomocí dvojice
čísel vrcholů (vrcholy číslujeme od nuly).
Formát výstupu:
Vypište celkem M řádků popisujících barvy hran ve stejném pořadí, jako byly
na vstupu. Barva každé hrany je buď 0 (černá), nebo 1 (červená, na obrázku šedá).
Pokud graf nejde správně obarvit, vypište jediný řádek obsahující číslo -1.
Ukázkový vstup:
7 9
0 1
0 2
1 3
2 3
2 4
3 5
4 5
4 6
5 6
Ukázkový výstup:
0
1
1
0
0
0
1
0
1
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Řešení
„To zní úplně jako sen!“ vykřikla nadšením dáma v klobouku.
„A to ještě není všechno,“ pokračoval Dalimír, „starat se o takový dům
není sranda. Proto také od nás máte k dispozici komorníka, uklízečku,
zahradníka, osobního šoféra a hlídače k vašim službám. Součástí je také
finanční dar, který by měl stačit na veškerou údržbu na alespoň dalších pět až
deset let.“
„A tento dům se všemi jeho výhodami jsme připravili… Chvíle napětí… Pro
vás, slečno!“ ukázal na dámu v klobouku.
„To… to je naprosto úžasné,“ rozpačitě děkovala dáma, „určitě se budu
snažit vás nezklamat a budu domu dělat dobré jméno. Určitě vám dokážu, že si
jej zasloužím.“
„Ano, ano. Uvnitř na vás čeká komorník, který Vám vše ukáže,“ ukazuje na
vchod Dalimír, „tak se běžte seznámit a my ostatní budeme pokračovat dál.“
Tak to je teda hustý, říkám si pro sebe. Jestli všechny domy budou takový, tak
jsem totálně za vodou.
„Nyní přicházíme ke druhému domu,“ znova mluví Dalimír, „tento dům se
pyšní těmi nejmodernějšími technologiemi, které doposud lidstvo vyvinulo.
Nejen že budete mít k dispozici ty nejlepší počítače a další hračky, ale
ještě k tomu vám každý rok budeme dodávat nové. Společnost vám budou dělat
domácí roboti, kteří za vás vysají, automaticky ovládaní droni, kteří doletí
ke dveřím pro poštovní zásilky, vyzvednou krabici s jídlem, a čeká na vás
ještě fůra dalších technologických vychytávek. Navíc je všechno centrálně
ovladatelné a synchronizované. Když na to přijde, tak celý den nebudete muset
vylézt z postele, a přitom se o všechno zvládnete postarat. Vysokorychlostní
internet a pokrytí Wi-Fi v celém areálu je samozřejmostí.“
„Tak to už se nemůžu dočkat, až se nastěhuju, to je přesně pro mě,“ ušklíbla
se ironicky hipsterka. Všichni už jsme tušili, kdo bude novým vlastníkem domu.
Vyhublému ajťákovi začaly svítit oči a pozorně poslouchal každé slovo jako do
té doby nikdy.
Vtom se zablesklo a před domem se objevil urostlý muž s mečem v ruce. Na jeho
rukou a nohou probleskovaly pruhy modrého světla. Pár vteřin tam stál,
rozhlížel se, ale pak se zase zablesklo a byl fuč.
„A teď jste mohli vidět… To byla asi… ukázka automatického zastrašování
pomocí holografické stráže,“ pokračoval Dalimír, „není to ale jediný
bezpečnostní prvek, který zde je. Celý areál je pokrytý kamerami, které
zevnitř můžete sledovat z libovolného přístroje a vstoupit můžete jen po
identifikaci svou oční duhovkou.“
„Jak už asi tušíte, tak tento dům je přímo dělaný pro vás, pane,“ ukázal na
ajťáka a ten se zaradoval: „Já… nemůžu se dočkat až si všechny tyhle super
věci vyzkouším a pořádně nakonfiguruji! Tenhle dům je to nejlepší, co jsem
zatím ve svém životě viděl!“
„Běžte ke vchodu. Tam vám kolega naskenuje duhovku a provede další
inicializaci. My budeme pokračovat dál,“ povídá Dalimír.
„Nyní přicházíme ke třetímu domu. V tom se určitě nikdy nudit nebudete!
Uvnitř najdete bowlingové dráhy, kulečník, saunu, minikino s vířivkou,
venkovní párty bazén, minigolfové hřiště a kroketové hřiště. Ať budete chtít
podniknout cokoliv, nikdy nebudete muset chodit moc daleko…“
 28-4-5 Hra kroket (11 bodů)
28-4-5 Hra kroket (11 bodů)
Ve hře kroket přesouváme míček po hřišti pomocí několika úderů holí. Míček
považujme za bod nulové velikosti, který se po úderu pohybuje po úsečce.
Celá trasa míčku tedy tvoří lomenou čáru. Na hřišti jsou také rozmístěné
branky, které si budeme představovat jako úsečky. Cílem hry je, aby míček
projel všechny branky, a to v předepsaném pořadí. Navíc každá branka má
určený směr, kterým je třeba ji projet.
Na vstupu dostanete startovní a cílovou pozici míčku a seznam branek (každá
je určena svými krajními body). Najděte nejkratší trasu míčku, která začně
na startu, skončí v cílovém bodě a projede všechny branky správným směrem
a ve správném pořadí.
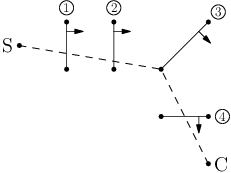
Jednoduchý příklad vstupu naleznete na obrázku.
Plnou čarou jsou značeny branky, šipky a čísla u nich udávají očekávané pořadí
a směr průjezdu. Čárkovaná čára ukazuje správnou nejkratší trasu míčku.
Ještě dodáme, že je povoleno projet stejnou branku vícekrát, stačí, aby jeden
z průjezdů dodržel správné pořadí a směr. Například je korektní projet branky
v pořadí 1, 2, 4, 3, 4, protože když nepočítáme první průjezd čtvrtou brankou
(který tím pádem může být i špatným směrem), dostaneme správné pořadí.
 Lehčí varianta (za 7 bodů): Všechny branky jsou svislé, projíždějí se zleva doprava
a jejich x-ové souřadnice tvoří rostoucí posloupnost (nejdřív je třeba
projet nejlevější branku, potom druhou nejlevější, …, až nakonec nejpravější).
Start je nalevo od všech branek a cíl napravo. Jinými slovy, stačí hrát
jen zleva doprava.
Lehčí varianta (za 7 bodů): Všechny branky jsou svislé, projíždějí se zleva doprava
a jejich x-ové souřadnice tvoří rostoucí posloupnost (nejdřív je třeba
projet nejlevější branku, potom druhou nejlevější, …, až nakonec nejpravější).
Start je nalevo od všech branek a cíl napravo. Jinými slovy, stačí hrát
jen zleva doprava.
Řešení
„… Součástí je také bar a taneční klub, který můžete použít jak pro
soukromé účely, tak pro pořádání veřejných akcí. Personál včetně DJe od nás
samozřejmě máte k dispozici. Pak vzadu můžete provozovat vlastní tetovací
salón, vedle něhož najdete skleník, kde roste takové zelené překvapení,“
dokončuje vyčerpávající popis Dalimír.
„Tak počkat! Co myslíte tím zeleným překvapením? A vůbec mám takový pocit,
že pořádání párty v obytné čtvrti je zakázané. Ty určitě budou narušovat noční
klid…“ začal jej okamžitě napomínat student.
„Tak tím zeleným překvapením jsem samozřejmě myslel bio okurky a domácí
zelí,“ vysvětluje Dalimír a při tom nepatrně mrkne na hipsterku, „co jste
myslel vy? A o rušení nočního klidu nemějte obavy. Celý areál je vybaven
moderním odhlučňovacím systémem, takže s tím by neměl být absolutně žádný
problém.“
Dalimír pokračuje: „A pro koho máme přichystaný tento dům? Ano, jste to vy,
zelenovlasá dívko!“
Hipsterka radostně naběhla dovnitř a my ostatní pokračovali dál, k domu číslo
čtyři.
„Nebudeme to dál napínat. Další dům je určen zde pro našeho věčného studenta
a můžeme jej klidně nazývat Domem vědomostí,“ představuje čtvrtý dům Dalimír.
„Součástí tohoto domu je obrovská knihovna, ve které jsou k dispozici
všechny studijní materiály, odborné články a literatura, které v posledních
50 letech lidstvo vyprodukovalo. K tomu je dodána přehledová brožura
k bezprobémové orientaci v celém archivu. Navíc jsme Vám zařídili licenci pro
sledování přednášek z pěti největších univerzit na světě. Kdyby Vám přeci jen
něco chybělo, nebo vyšel nějaký nový článek, který byste chtěl, neváhejte nám
říct a my jej pro vás obstaráme. Dále kolem domu máte dost prostoru pro
pěstování ovoce, zeleniny, bylinek a obilovin, které byste k životu mohl
potřebovat. Dodáme Vám ještě několik profesionálních ekologických zahradníků,
kteří s Vámi na pěstování budou spolupracovat. Společně toho pravděpodobně
vypěstujete více, než budete potřebovat, a jelikož pozemek patří Vám, tak vás
přebytek nejspíš i uživí. A málem bych zapomněl, to auto, které tady stojí, je
Váš nový elektromobil, šetrný k životnímu prostředí,“ dokončuje Dalimír.
„Tak to je naprosto boží! Tohle je doslova a do písmene můj sen! Živý, tady,
přede mnou a ještě k tomu patří mně! Vůbec nevím, jak Vám mám poděkovat,“
povídá student, ale není na něm vidět žádná výraznější emoce.
„Jen mi neděkujte a raději se běžte zabydlet,“ posílá jej Dalimír dovnitř.
„Tak teď ještě vyřešit vás,“ říká směrem ke mně, „dům pro vás je ještě
kousek dál po cestě.“
Přicházíme ke znatelně menšímu domu, než byly všechny předchozí, který na první
pohled vypadá naprosto obyčejně.
Dalimír začíná představovat: „Pro vás máme postavený klasický rodinný dům
čtyři plus jedna. Oproti běžným tři plus jedna má navíc druhou ložnici, která se
na takto odlehlém místě určitě bude hodit a případně se dá přestavět na dětský
pokoj. K domu patří menší zahrada vhodná pro letní posezení venku. Jinak je to
klasický byt. Kuchyň je vybavena sporákem a myčkou, obývák televizí a DVD.
Také pro vás máme Volkswagena. Je sice trochu ojetý, ale zase málo žere …
A kdybyste měl zájem, tak vás doporučíme do jedné telefonní společnosti, kde
zrovna shání zdatného technika. To jste vystudoval, je to tak?“
„Ano, je to tak,“ odpovídám.
„Tak to je asi všechno. Jak se Vám to líbí?“ dokončuje a ptá se Dalimír.
Já na to rozpačitě odpovídám: „No… ano, líbí… Samozřejmě, že líbí.
Ale… je tu jedna věc, která mi vrtá hlavou… Ostatní dostali výrazně větší
a luxusnější domy a v podstatě se jim dneska splnily všechny sny, zatímco pro
mě máte »jen« takovýhle »obyčejný dům«?“
Dalimír hned reaguje: „Rozumím. Tento dar od nás nemusíte přijmout. Pořád
máte možnost jej odmítnout. Jsem si celkem jistý, že získáním tohoto domu
budete ve značně lepší situaci, než jste byl před týdnem…“
„Ano, ano. Já si určitě nechci stěžovat. Jsem samozřejmě nadšen a vaši
nabídku přijímám všemi deseti! Jen mě trochu zaskočil ten nepoměr vůči
ostatním. Ale už raději mlčím,“ vymlouvám se.
„Tak to bude nejlepší,“ říká Dalimír, „já bych si dokonce vsadil, že
se svým novým obydlím budete spokojený. A kdo ví, jestli ne dokonce víc než ostatní? Tak se běžte dovnitř trochu porozhlédnout, já teď ještě musím dořešit
pár věcí a trochu si to všechno utřídit.“
 28-4-6 Mediánové třídění (9 bodů)
28-4-6 Mediánové třídění (9 bodů)
Máme dohromady N čísel k setřídění. Také máme takovou speciální krabičku.
Té na začátku zadáme fixní liché K a pak do ní začneme postupně vkládat
nějaké prvky. Po každém vloženém prvku nám krabička řekne medián z posledních
K vložených prvků, tedy takový prvek, který by se po jejich setřídění
nacházel na prostředním místě. Krabička začne vracet mediány teprve poté, co
do ní vložíme alespoň K prvků.
Například pokud pro K=3 do krabičky vložíme postupně prvky 4, 7, 1, 2, 3, 5,
řekne nám hodnoty ∅, ∅, 4, 2, 2, 3 (kde ∅ značí
prázdný výsledek, když krabička obsahuje méně než K prvků). Například první
dvojka je mediánem posloupnosti 7, 1, 2.
Vymyslete, jak s pomocí takovéto krabičky setřídit čísla v linárním čase.
K si můžete zvolit libovolné, klidně pro každý vstup jiné. Předpokládejte,
že přidání prvku do krabičky trvá konstantní čas.
Řešení
Po tom dni a podepsání všech smluv jsem Dalimíra už nikdy neviděl a o Druhé
šanci nikdy neslyšel.
* * *
Od té doby se u nás v ulici ledacos změnilo. Teď když procházím kolem prvního
domu, tak z něj věčně slyším křik a hádky. Dáma už se za tu dobu stíhá potřetí
rozvádět. Nikdo pro ní není dost dobrý. Co na tom, že vlastní úspěšný
salón krásy a večeří kaviár? Co na tom, že vyhrává všechny soudní spory
o majetek a děti, když žádnému z nich nemůže dopřát pocit fungující rodiny
a namísto mateřského objetí jim pronajímá chůvu, aby se mohla naplno věnovat
svému účesu a nehtům. Tato dáma dostala před deseti lety neuvěřitelné
možnosti. Bohužel se ale snažila urvat více, než dokázala sama unést. Dělala
spoustu věcí, které nebyly zrovna správné, ale dělala je prostě jen proto, že
si je mohla dovolit. Podle mě teď určitě nevede život, jaký si předtím vysnila.
Blížím se ke druhému domu. U něj je zaparkovaná blikající sanitka. Už zase…
Vyhublý ajťák se totiž všemi technologiemi a vymoženostmi nechal natolik
unést, že jen zřídkakdy vycházel ven. Dnešní svět to bohužel umožňuje. Když se
nad tím zamyslíte, tak už vlastně neexistuje mnoho věcí, které by se nedaly
zařídit online. Jeho život byl naprosto oddán virtuální realitě a moderním
technologiím. Bohužel virtuálnímu světu dával výraznou přednost před tím
fyzickým a ignoroval potřeby svého vlastního těla. A tak začal trpět
ochabnutím svalů, záněty zápěstí a nakonec se mu začala bortit páteř.
Před necelým rokem ochrnul na dolní polovinu těla, když upadl na zem po
cestě na záchod. Zachránili jej až kamarádi z online hry, když se do ní dva dny
po sobě nepřipojil a ani o sobě nedal vědět. Dostat se pak k němu
a poskytnout mu lékařskou pomoc byl také problém. Projít přes všechna
technologická zabezpečení, která v domě měl, by byl úkol minimálně pro CIA.
Ještě že měl jen obyčejná skleněná okna.
Po tomto incidentu mu byl přidělen osobní pečovatel. Ten se následně stal jeho
nejbližším přítelem ve fyzickém světě za všechny ty roky. Vlastně byl zároveň
jediným člověkem, který trávil v jeho přítomnosti více jak deset minut denně.
Když jsem míjel jeho dům, zrovna se sanitka rozhoukala a začala odjíždět.
 28-4-7 Jízda sanitkou (11 bodů)
28-4-7 Jízda sanitkou (11 bodů)
Sanitka má naloženého stabilizovaného pacienta a potřebuje jej bezpečně odvézt
z jeho domu do některé z nemocnic. Ve městě ale probíhají na různých místech
opravy, v jejichž okolí to nebezpečně drncá a navíc poblíž nich hrozí
uvíznutí v zácpě. Proto by se řidič rád držel od míst oprav co nejdál.
Máte zadanou mapu města jako čtvercovou mřížku s vyznačenou počáteční
pozicí, pozicemi nemocnic a pozicemi všech míst, kde probíhají opravy.
Najděte největší K takové, že existuje cesta ze startu do nějaké
nemocnice, která se po celou dobu drží ve vzdálenosti alespoň K od
všech míst oprav. Zároveň také najděte libovolnou cestu splňující toto omezení.
Po mapě se pohybujeme pouze vodorovně a svisle.
Vzdálenost měříme v manhattanské metrice, tedy jako
součet rozdílů x-ových a y-ových souřadnic. Například políčka (1,2)
a (5,3) mají vzdálenost 4+1 = 5.
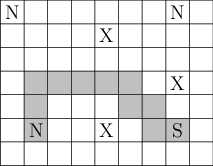
Pro následující mapu (S značí start, N nemocnici a X místo oprav) je
největší K=2 a jedna z možných optimálních cest je vyznačena šedě.
Snadno nahlédnete, že pro K=3 žádná cesta neexistuje.
Řešení
Ve třetím domě byl klid. Nedá se to vůbec srovnávat s tím, co se tam dělo před
pěti až deseti lety. Bývala tam divoká párty minimálně každý druhý den, která
se bez výjimky protahovala minimálně do pozdního rána dalšího dne. Já sám jsem
se tam také dvakrát vydal a můžu říct, že to bylo super! Pak jsem ale další
dva dny téměř jen ležel, spal a střízlivěl. Takovouhle akci bych dokázal
přežít maximálně dvakrát měsíčně, tak je pro mě naprosto nepochopitelné, že to
ta zelenovlasá, dnes už černovlasá, hipsterka zvládla táhnout přes čtyři roky
v kuse zhruba čtyřikrát týdně.
Celou dobu to vypadalo, že si vše maximálně užívá. Pak ale jednou z ničeho
nic, když se párty zase dobře rozjela, proskočila zavřeným oknem a dopadla
přímo do bazénu. Nic vážného se jí nestalo a nikdo přesně neví, proč to
vlastně udělala. Nikdo jí v té době nebyl dost blízký, aby dokázal něco tušit,
natož pak předpovídat. Z tohoto incidentu se ale nedokázala vzpamatovat
a další skoro dva roky strávila na psychiatrickém oddělení. Asi to holka s tou
volností, spontáností a nevázaností přehnala. Žila naplno každý moment a jen
pro ten moment. Už si ale nenašla chvilku, aby se sama ohlédla odkud, kam, za
čím, pro koho a proč jde. A tak se jí tyhle nevyřešené a odkládané pocity
hromadily tak dlouho, až to najednou vybouchlo.
Dneska ale žije docela jiný život. Našla si stálého přítele a společně přízemí
jejího domu přestavěli z nočního klubu na moderní školku. Jsme spolu přátelé
a občas se navštěvujeme. Myslím si, že navzdory svému divokému mládí je to
celkem fajn a rozumná holka.
Teď už se blížím ke čtvrtému domu. Tam se toho za těch deset let moc
nezměnilo. Předtím tam žil podivný věčný student, jehož život byl řízen
přísnými pravidly. Dnes tam žije podivný věčný student, jehož život je řízen
ještě přísnějšími pravidly. Akorát nyní má svou sbírku titulů obohacenou
o mnohé další obory. Každý den vstává a chodí spát ve stejnou dobu, má pečlivě
navržený jídelníček, třikrát týdně cvičí a vůbec v jeho životě není žádná
nepravidelnost. Namísto kamarádů má pouze spolupracovníky a spolubadatele.
Ze začátku jsem jej párkrát zkusil někam pozvat, ale v jeho rozvrhu se těžko
dá hledat minuta, která by nebyla zabraná v rámci jeho složitého týdenního
režimu. Teď o něm absolutně nedokáži říct, zda je v životě šťastný a zda má
to, co hledal. Nerozumím mu, nemáme si spolu co říct, emoce na sobě nedává
znát, ale třeba je tak šťastný.
Teď už se konečně blížím ke svému domu. Tam na mě čeká manželka a mé dvě
krásné děti, pro které jsem na zahradě v posledním roce postavil malé dětské
hřiště. Myslím, že teď žiju spokojený život, ve kterém ještě stále jdu za svým
cílem. Posledních deset let pro mě nebylo vždy jednoduchých. Musel jsem se
hodně snažit v práci a dělat přesčasy, abych získal vyšší kvalifikaci a zvedli
mi plat. Doma nám zas nedávno prasklo potrubí a děti jsme museli složitě
dovážet k babičkám a vůbec celkem často musíme řešit takové náhlé problémy.
Ale zatím jsme to vždy všechno nějak zvládli.
Jsem opravdu rád, že mi kdysi byl přidělen právě tento dům a ne žádný jiný. Jsem opravdu spokojený. V tom se tehdy Dalimír trefil.
Všem mým sousedům se v ten den splnil jejich sen a začali si hlavně užívat
a po nějaké době se toho přesytili. Nikdy v životě se nenaučili, jak o věci
v životě bojovat a jak se o své cíle snažit. Já oproti nim dostal jen
podmínky, které mi umožňovaly si za svými cíli jít a snažit se je plnit.
Samotný fakt, že se mi to daří a postupně za mnou jsou vidět výsledky, mě
naplňuje opravdovým štěstím. Takovým tím pocitem zadostiučinění, který moji
sousedé dlouho nebo dokonce nikdy neměli šanci poznat.
Oni do náruče dostali svůj cíl a v tom okamžiku se přestali zajímat o jakoukoliv
cestu, která by je někam mohla dovést. Já jsem dostal možnost stavět si svou
vlastní cestu a jít po ní. A to je přesně ono, protože právě ta cesta je můj
cíl! Ano, je to tak: „Cesta je cíl!“
Příběh pro vás napsal
Karel Tesař
 28-4-8 Strojové učení (20 bodů)
28-4-8 Strojové učení (20 bodů)
Co je to strojové učení?
Lidské učení je schopnost adaptace na nové situace. Když budeme poprvé hrát
šachy, asi nám to nepůjde moc dobře, ale podruhé to půjde trochu lépe, a když
budeme hrát dost dlouho, můžeme se stát experty. Můžeme se naučit hrát dobře
šachy, i když na začátku dostaneme jenom jejich pravidla, která nám umožňují
dělat špatné i dobré tahy. Nikdo nám nedá přesný postup, jak být expert –
v naší hlavě hraním šachů vznikne schopnost hrát je dobře.
Strojové učení se snaží replikovat tuhle schopnost v počítačích. Je velmi
užitečné umět řešit problémy, na které neznáme žádné jasné algoritmy.
To platí obzvlášť, když se snažíme automatizovat nějaký aspekt lidské inteligence.
Jedna praktická aplikace je třeba počítačové vidění. Dnes počítače umí
číst psaný text, rozeznávat lidské tváře, nebo třeba hledat ve fotkách dopravní
značky, a to všechno s nadlidskou přesností. Algoritmus strojového učení
například dostane 5 000 příkladů 10 různých dopravních značek a jeho výstupem
bude postup, jak je od sebe rozpoznat.
Většina materiálů o strojovém učení je buď v angličtině nebo používá
anglickou terminologii. Aby pro vás bylo snadnější si dle zájmu dohledat víc
informací, budeme české termíny zavádět i s jejich anglickými ekvivalenty.
Jestli byste chtěli strojovému učení věnovat víc samostudia, můžete si třeba
najít materiály ke kurzu
Machine Learning na Courseře,
nejbližší termín kurzu začíná 21. března.
Druhy strojového učení
Strojové učení se dělí na tři široké kategorie: učení s učitelem
(supervised learning), bez učitele (unsupervised learning) a
zpětnovazební učení (reinforcement learning).
Zmíněný problém klasifikace dopravních značek patří pod učení s učitelem.
Jakýsi učitel nám ukázal příklady a řekl nám „tohle je stopka“, „tohle je
zákaz vjezdu“, a tak dále. Naším úkolem je podle těchto trénovacích dat
vyrobit algoritmus, který bude fungovat dobře nejen na příkladech, které jsme
dostali od učitele, ale i na těch, které jsme ještě nikdy neviděli.
Učení bez učitele se snaží najít nějaké pravidelnosti, ale nemá zvenku zadáno,
čím se takové pravidelnosti budou vyznačovat. Když máme nějakou sadu dat,
o které nic nevíme, učení bez učitele nám třeba může pomoct najít nějaké
jejich „významné vlastnosti“, na které se pak můžeme zaměřit zvlášť. Mezi učení bez učitele
patří třeba detekce anomálií, která hledá ve vstupních datech vzorky,
které významně vybočují z „pravidelné struktury“. Když třeba máme datacentrum
plné serverů, můžeme se snažit detekcí anomálií najít servery, se kterými je
něco nějakým způsobem špatně, i když předem nevíme, jakým způsobem se mohou
porouchat a jak se to projeví v parametrech, které měříme.
Zpětnovazební učení je o něco speciálnější. Používá se na učení chování
v prostředí, ve kterém nemusí být podle výstupu naučeného systému hned jasné,
jestli se chová chytře. Představte si třeba, že se snažíme naučit hrát Pacmana.
Algoritmu říkáme, jak vypadá labyrint, kde se Pacman nachází, kde jsou duchové a kde je jídlo
a on nám říká, kam chce, abychom šli. Chceme, aby se naučil, jak se má
hýbat, aby sežral co nejvíc jídla a pokud možno neumřel.
Když algoritmus řekne „jdi vlevo,“ tak nevíme hned, jestli to byl dlouhodobě
dobrý krok, nebo špatný krok – to záleží na tom, jak se algoritmus zachová
v budoucnosti (například jestli ho vlivem tohoto kroku za 5 tahů zabije duch).
Pacman provádí posloupnost akcí v nějakém prostředí a snaží se, aby se nakonec
naučil co nejlepší algoritmus pro hraní.
Učení bez učitele na to použít zřejmě nejde (protože máme konkrétní cíl –
snažíme se maximalizovat snědené jidlo). Učení s učitelem se taky nehodí.
Intuitivně bychom se totiž neučili hrát dobře – učili bychom se jenom
napodobovat učitele. Pokud by tedy učitel byl třeba mistr světa v Pacmanovi,
tak by ho náš naučený algoritmus neuměl porazit, protože se jenom naučí to, co
umí učitel. Náš cíl je najít co nejlepší algoritmus, který je v rámci pravidel
Pacmana možný.
Dnes si ukážeme pár základních algoritmů učení s učitelem.
Učení s učitelem
Zkusme se třeba naučit podle výšky a obvodu pasu předpovídat váhu lidí.
Nejdříve najdeme nějaké dobrovolníky (nechť je jich N) a posbíráme jejich
výšky, obvody a váhy. Vstupním informacím, podle kterých se snažíme předpovídat
hmotnost, říkáme příznaky (features). Počet příznaků, tedy
u nás 2, označíme jako p; první příznak je výška a druhý je obvod pasu.
Uložíme si je do vektorů x(1), x(2), …, x(N).
To, co se snažíme naučit předpovídat – tedy váhu – si uložíme do y(1),
… y(N).
Všem vstupním i výstupním datům, se kterými pracujeme, se říká souhrnně
dataset. Označíme jej jako D.
Když třeba
x(8) = (1.87, 93) a
y(8) = 85, tak osmý dobrovolník měřil
1.87 m, měl obvod pasu 93 cm a vážil 85 kg. Informacím, které máme o jednom
dobrovolníkovi, tedy dvojici
(x(8), y(8)), říkáme společně
vzorek (
sample). Používáme standardní vektorové značení, takže
x=1.87 a
x=93.
Většina aplikací učení s učitelem je klasifikace nebo regrese.
Klasifikace je přiřazení vstupního vzorku do jedné z kategorií. Regrese
je předpověď hodnoty nějaké funkce, která vede do reálných čísel. Předpovídání
hmotnosti je regrese. Určování, jaký typ dopravní značky jsme vyfotili, je
klasifikace.
Náš cíl je najít nějakou funkci f takovou, že pokud možno pro každý vzorek
(x,y) je y = f(x), nebo aspoň mezi nimi nebude velký rozdíl. Kromě toho ale
chceme ještě jednu důležitou vlastnost: f by měla dobře generalizovat.
Učení je hledání vhodné funkce f.
První požadavek, tedy aby f na známých vzorcích odpovídala správně, se dá
splnit spoustou způsobů. Jeden z nich je třeba ten, že by si f při učení
zapamatovala všechna trénovací data, a když by dostala vstup x, tak by se
podívala, jestli tenhle vstup byl v trénovacích datech, a jestli byl, vrátila
by jeho příslušný výstup, a jinak by vrátila třeba 9 999.
Máte-li nepříjemný pocit, že na tomhle nápadu je něčo špatně, máte ho zcela
správně.
Taková funkce f by fungovala perfektně na trénovacích datech, ale jakmile
bychom chtěli předpovědět hmotnost někoho, koho jsme ještě neviděli, byla by
zcela k ničemu. Generalizace je právě tato schopnost fungovat dobře i
na lidi, které jsme při učení ještě neviděli.
Příznaky
Když chceme mít dobré předpovědi, samozřejmě velmi záleží na tom, abychom
zvolili dobré příznaky. Musí obsahovat nějakou užitečnou informaci, na které
závisí ta veličina, kterou předpovídáme. Když se snažíme naučit předpovídat
hmotnost lidí, nejspíš nám pomůže vědět fyzikální vlastnosti, které s hmotností
souvisí: třeba výšku, obvod pasu, věk nebo procento tuku v těle. Naopak nám
asi nepomůže vědět barvu očí nebo oblíbenou kapelu.
Než spustíme algoritmus strojového učení, vyplatí se nejdřív zamyslet
nad reálnou strukturou problému a zkusit pro něj vymyslet co nejužitečnější
příznaky. Zkusme třeba předpovídat podle výšky a hmotnosti pravděpodobnost
srdeční příhody v následujícím roce. Samotná hmotnost a výška sice jsou užitečné
informace (když vážím 250 kg, jsem rizikovější, než kdybych vážil 70 kg), ale
lepší nejspíš bude si přidat jako příznak BMI
((hmotnost v kg)/(výška v m)2). BMI zohledňuje, že různí
lidé mají různou postavu – je asi zdravější vážit 100 kg a být vysoký 2 metry,
než vážit 80 kg a být vysoký 1.5 metru.
Příznaky jde široce dělit na kategorické a numerické. Numerické příznaky se dají
přirozeně vyjádřit jako číslo, třeba výška v centimetrech nebo barva pixelu
v obrázku. Kategorické příznaky můžou být třeba krevní skupina nebo státní
občanství. Existuje pro ně nějaký poměrně malý počet možných hodnot (třeba
krevní skupiny jsou {0+, 0-, A+, A-, B+, B-,
AB+, AB-}) a na těhle
hodnotách nemusí dávat smysl obvyklé číselné operace.
Mohli bychom sice třeba označit krevní skupiny místo názvů pořadovými čísly
(0+ = 1, …, AB- = 8), ale operace nad takovým
označením nejsou užitečné – sice nad naším označením můžeme tvrdit, že
(0-) + (B-) = (AB-), ale to neodpovídá žádnému vztahu v reálném světě.
Stejně tak není B- v žádném smyslu „větší než“ 0+. Oproti tomu
třeba může dávat smysl porovnávat výšky dvou lidí nebo počítat jejich rozdíly.
Hodně algoritmů potřebuje, aby jejich vstupy byla čísla.
Tehdy potřebujeme kategorické příznaky „zakódovat“ do
číselných. Nejobvyklejší takové kódování z příznaku, který obsahuje jednu
z K kategorií, vyrobí K číselných příznaků, jeden pro každou kategorii.
Když vzorek patří do i-té kategorie, nastavíme i-tý příznak na 1 a ostatní
na 0.
Předpokládejme, že existuje nějaký skutečný vztah fˆ, který
z x dělá y (tedy z výšek a obvodů pasu dává hmotnost). Příznaky, které
měříme, ale nemusí stačit na zcela přesnou odpověď: i když mají Jana a Katka
stejnou výšku a obvod pasu, můžou mít jinou hmotnost, protože se Katka
ráno nenasnídala. Existuje nějaký vliv vnějších příznaků, které neměříme (nebo
možná ani z principu měřit nejdou – třeba máme nepřesnou váhu).
Dá se to neformálně napsat jako y = fˆ(x) + ε:
předpovídaná hodnota y se skládá ze složky, která závisí na x,
a nějakého náhodného (a snad malého) ε, ve kterém jsou schované
vlivy, které neumíme měřit.
Funkci f, kterou se snažíme naučit, se říká model – snaží se co
nejpřesněji modelovat, co by dělala fˆ, kdybychom se jí mohli
zeptat.
Měření chyby modelu
Po modelech chceme, aby byly co nejpřesnější a aby dobře generalizovaly.
Chceme tedy, aby na neznámém vzorku, který nebyl k dispozici učícímu
algoritmu, daly dobrou předpověď.
Existují různé metriky pro to, jak dobrá předpověď je. Většina z nich jsou
nějaká míra chyby.
Pro naše předpovídání hmotnosti se třeba hodí velmi obvykle používaná
kvadratická odchylka. Kvadratická odchylka modelu f na vzorku (x,y)
je rovna (y - f(x))2. Intuitivně jí velké odchylky vadí mnohem víc než malé.
Pro klasifikační úlohy se jako metrika hodí accuracy (Kromě accuracy
se pro klasifikátory měří i metriky precision a recall.
České překlady tady bohužel nemají tak dobře zavedený význam,
jako anglické termíny.).
Accuracy na jednom vzorku je 1 tehdy, pokud jej f předpoví správně, a 0, když
na něm udělá chybu. Když třeba předpovídáme, jakou dopravní značku obsahuje
obrázek, zajímá nás jenom, jestli najdeme tu správnou. Když si spleteme stopku
se zákazem vjezdu, je to pro accuracy stejně špatné, jako bychom si ji spletli
s přikázaným směrem jízdy.
Zatím jsme si ukázali definice dvou různých chyb modelu na jednom vzorku.
Po modelu chceme, aby měl co nejmenší střední hodnotu chyby, neboli
aby na náhodně vybraném neznámém vzorku byl co nejpřesnější.
Když máme nějaký model f, jak zjistíme střední hodnotu chyby na neznámém
vzorku? Neznámé vzorky jsou pro nás nedostupné – nemůžeme jít změřit 7 miliard
lidí a spočítat, jakou chybu průměrně děláme. Máme k dispozici jenom
data od dobrovolníků. Dělá se to tak, že učícímu algoritmu nedáme všechna data,
která máme. Rozdělíme dataset D na trénovací množinu S a
testovací množinu T, třeba v poměru 90 %/10 %. Učícím algoritmům
dáme k dispozici jenom trénovací data. Testovací vzorky před ním skryjeme. Až
nám učící algoritmus dá model f, spočítáme jeho průměrnou chybu na testovací
množině. S trochou statistiky se dá ukázat, že průměrná chyba na testovací
množině rozumně odhaduje střední chybu na všech neznámých vzorcích.
Úkol 1 [1b]
Je potřeba, aby rozdělení na testovací a trénovací množinu bylo náhodné.
Ať dataset D obsahuje nejdřív 100 značek „stop“, pak 100
značek „dej přednost v jízdě“ a nakonec 100 značek „slepá ulice“.
Vymyslete, co a jak by se mohlo rozbít, kdybychom testovací množinu vybrali
nenáhodně.
Když třeba po modelu chceme malé kvadratické odchylky, chceme malou
střední kvadratickou odchylku na neznámých datech. Tu odhadneme
podle střední kvadratické odchylky na testovací množině T:
E ≈ E
T =
MSET =
∑
(x,y)∈T (y-f(x))
2.
Střední kvadratické odchylce se říká anglicky mean square error
(MSE).
Když nás zajímá accuracy na neznámých datech, odhadneme ji podobně: pomocí
průměrné accuracy na T.
Čím více dat dáme k dispozici algoritmu strojového učení, tím více se jim bude
moct přizpůsobit a tím bude naučený model dávat přesnější předpovědi.
Na druhou stranu, čím větší máme testovací množinu, tím přesněji chyba na
testovací množině ET odhadne skutečnou chybu na neznámých vzorcích E.
Vzpomeňte si na f, která si uložila všechna trénovací data do tabulky a na
všechno kromě nich vrátila 9 999. Takový model má na trénovacích datech nulovou
chybu (ES=0). Na testovacích datech T, která nemá v tabulce,
ale odpoví strašně špatně, takže průměrná chyba na testovacích datech
ET nám správně řekne, jak strašně moc špatný tenhle model je.
Přeučení a porovnávání modelů
Pokud se naučíme model, který je hodně dobrý na trénovacích datech, ale
podstatně horší na testovacích datech, může to být kvůli přeučení
(neboli overfittingu).
K přeučení dochází, pokud učícímu algoritmu umožníme, aby se příliš silně
adaptoval na nějaké zvláštnosti trénovacích dat, které ale obecně neplatí.
Hodně algoritmů strojového učení funguje tak, že postupně po epochách
víc a víc adaptuje model na trénovací data. Vyrobí tedy posloupnost modelů
f1, f2, … , ve které jsou modely postupně čím dál tím adaptovanější
na trénovací data, ale po nějaké době se začnou přeučovat, a tedy začnou být
míň užitečné pro obecné použití.
Podobná situace nastane, když zkoušíme na jedněch datech různé algoritmy
strojového učení a chceme z naučených modelů vybrat ten nejvhodnější.
Očividný přístup, jak vybrat z modelů f1,f2,… ten nejlepší, je změřit
chybu všech modelů na testovacích množině a vrátit ten, který ji má nejmenší,
ale tenhle přístup je rozbitý.
Proč je rozbitý? Vzpomeňte si, že testovací množina se používá k odhadování
skutečné chyby. Když si z modelů vybereme ten, který na nejmenší testovací
chybu, bude jeho testovací chyba příliš optimistický odhad skutečné
chyby.
Ilustrujeme si tenhle problém malým myšlenkovým experimentem.
Představte si, že naše modely jsou tři férové mince. Pokud padne panna, model
dá správný výsledek, a když padne orel, dá špatný výsledek. Každý model tedy
ve skutečnosti dá správný výsledek v 50 % případů.
Testovací množinu vyrobíme tak, že každou mincí desetkrát hodíme. Na první
vyjdou 3 orli, na druhé 7 orlů a na třetí 5 orlů. Vybereme si tedy druhý model
a budeme si o něm myslet, že je přesný v 70 % případů. To je víc než jeho
skutečných 50 % – druhý model jenom měl to štěstí, že při našem testu naházel
nejvíc orlů. Jsme moc optimističtí o jeho výkonu, a to o 20 %.
Co kdybychom neházeli třemi mincemi, ale 10 000 mincemi?
Skoro určitě (s pravděpodobností asi 0.99994) se stane, že náhodou některá
z nich nahází 10 orlů. Byli bychom extrémně optimističtí – mysleli bychom
si, že jsme našli minci, na které vždycky padají orli, i když je férová.
Přidání dalších modelů způsobilo, že náš odhad je horší – teď už se mýlíme
o 50 % místo 20 %.
Správné řešení je udělat „výběr nejlepší mince“ a „odhad
pravděpodobnosti“ jako nezávislé experimenty: nejdřív 10× hodit a vybrat
nejperspektivnější minci, a pak jí znova 10× hodit a podle druhých hodů
odhadnout její „cinklost“. Když jsme v první fázi vybrali minci, co naházela
10 orlů, ale ve skutečnosti je férová a jenom měla štěstí, tak druhá fáze pořád
bude 10 hodů férovou mincí a nejspíš nám řekne, že skutečná pravděpodobnost
padnutí orla na vybrané minci je 0.5.
Když vybíráme z více modelů ten nejlepší a pak chceme vědět, jaký výkon
od něho můžeme očekávat na nových datech, jedno ze správných řešení je rozdělit
data na tři množiny: trénovací, validační a testovací (třeba
v poměru 80 %/10 %/10 %). Trénovací množina se dá k dispozici učícím algoritmům
(nebo nad ní iteruje jeden algoritmus a leze z něj posloupnost modelů). Jako
nejlepší model vybereme ten, co má nejmenší chybu na validační množině.
Tím pádem „neznečistíme testovací množinu“ a budeme ji moci dál používat
k dobrému odhadování skutečné chyby.
Chyby na validační a testovací množině odpovídají naměřeným „cinklostem“
v první a druhé fázi myšlenkového experimentu s mincemi.
Teď už se trochu vyznáme v základních termínech a souvislostích, tak se konečně
vrhneme na něco programovacího.
Lineární regrese
Algoritmy obecného učení jsou si obecně hodně podobné:
- Předepíší, jaký obecný tvar budou mít modely f, které z nich budou padat.
Tenhle předpis bude obsahovat vstupní vektor x a nějaký vektor parametrů, který se označuje β. Konkrétní model dostaneme, když do
předpisu dosadíme parametry.
- Říkají, jakou chybu se snaží minimalizovat.
- Popisují, jak efektivně najít takové β, že předpis f s dosazenými
parametry β bude mít co nejmenší chybu.
Lineární regrese konkrétně:
- Hledá lineární model. Lineární model je funkce f,
která na vstupu x dá jako výstup f(x)=ϑ+ ∑ αi
xi. Konstanty ϑ a αi jsou parametry určující konkrétní
lineární model. Dohromady je těchto parametrů (p+1), tedy vektor parametrů
β je (p+1)-rozměrný: nejdříve obsahuje p složek β1=α1,
β2=α2, … βp=αp a pak jednu
složku β(p+1)=ϑ.
Graf lineárního modelu je přímka v p-rozměrném prostoru
(Pokud znáte skalární součin, všimněte si, že f(x→)=(x→, 1) ·(α→, ϑ) = (x→, 1) ·β.).
- Chyba, kterou minimalizuje, je střední kvadratická odchylka
na trénovací množině, proto se se jí taky říká metoda nejmenších
čtverců:
E=
MSES(β) =
∑
(x,y)∈S(y - f
β(x))
2.
- Efektivně najde dobrou hodnotu vektoru β pomocí gradientové
metody (Pro lineární regresi existuje i vzorec, ze kterého jde
nejlepší model přímo spočítat, ale gradientová metoda je jednodušší
na pochopení a obecnější – používá se ve spoustě dalších učících
algoritmů.).
Kdyby nám nezáleželo na času na naučení, stačily by nám první dva „moduly“.
Mohli bychom si jenom vygenerovat biliardu modelů (třeba pro všechny
hodnoty všech složek β od -100 do 100 s krokem 0.1), pro každý
spočítat chybu a vybrat ten, co ji má nejmenší. To ale rychle přestane být
efektivní pro hodně parametrů.
Úkol 2 [1b]
Jak závisí časová složitost tohohle hloupého přístupu „vygenerujeme si
tabulku se spoustou modelů a vybereme ten nejlepší“ na velikosti trénovací
množiny a počtu příznaků p?
Efektivnější minimalizace chyby vyžaduje trochu matematické analýzy.
O kvadratické chybě se dají dokázat užitečné vlastnosti. Zaprvé když si
vyjádříme E jako funkci parametrů β=(α1,… αp, ϑ),
zjistíme, že je spojitá. Zadruhé má E jediné lokální minimum, které je
i její jediné globální minimum. Zatřetí nemá žádné inflexní body.
Gradientová metoda
Gradientová metoda (gradient descent) umí takové funkce
minimalizovat. Obecně tato metoda funguje tak, že začneme
v nějakém libovolném, třeba nulovém počátečním bodu β0.
Potom se podíváme, kterým směrem bychom mohli trošku posunout β0
tak, abychom tím co nejvíc snížili E.
Je vám ten nápad povědomý? Je vám povědomý zcela správně. Ve druhém
díle seriálu jsme si ukazovali, jak
hledat „horolezením“ extrémy reálných funkcí. Gradientová metoda je
horolezení velmi podobná. Liší se tím, že „má kompas“ – umí najít
zlepšující bod v okolí efektivněji než náhodným zkoušením.
Kompasu se říká gradient. Gradient E v bodu β0 se značí
∇E(β0) a je to vektor, který říká, kterým směrem máme jít
z β0, abychom šli co nejstrměji směrem zvyšující se E. V každém bodu
může obecně gradient vést jiným směrem.
Když gradient otočíme, dostaneme směr největšího poklesu E.
Když je délka gradientu v bodě β velká, znamená to, že E
v β rychle roste/klesá. Naopak malý gradient znamená, že se
nacházíme v placaté oblasti a nulový gradient znamená, že β je lokální
minimum, maximum, nebo inflexní bod.
Protože E inflexní body nemá, značí v ní nulový gradient lokální minimum
nebo maximum.
Krok gradientové metody číslo t začne v souřadnicích βt-1.
Spočítá si v tomhle bodě gradient ∇E(βt-1), nějaký jeho
γ-násobek odečte od souřadnic a tím spočítá βt.
Jak velké má být γ? Čím menší, tím déle bude gradientová metoda běžet,
ale tím přesněji se zase trefí do lokálního optima. Když bude γ moc
velká, budou kroky gradientové metody lokální minimum „přeskakovat“, což se
projeví tak, že se po pár iteracích dostaneme k nekonečně velkým hodnotám
parametrů a nic se nenaučíme. Pokud se vám taková věc stane, zkuste
γ zmenšit o pár řádů.
Hodně učících algoritmů má podobný parametr ovlivňující velikost jednoho
učícího kroku. Většinou se mu říká learning rate, rychlost učení.
Po odečtení γ-násobku gradientu přejdeme na krok (t+1):
spočítáme gradient v βt, odečteme jeho γ-násobek,
a tak dále. Skončíme, když je splněné nějaké kritérium, například když už jsme
počítali dost dlouho nebo když je gradient hodně malý. Pokud gradientová metoda
skončí v místě, kde je gradient skoro nulový, našla lokální minimum.
Gradient je rovný nule i v lokálním maximu. Když bychom měli tu neuvěřitelnou
smůlu, že bychom začali gradientovou metodu dokonale přesně v lokálním maximu,
tak bychom hned skončili a vrátili lokální maximum. To se ale skoro určitě
nestane. Stane se možná, že začneme gradientovou metodu blízko lokálního
maxima. Potom nás od něho ale první krok trochu oddálí (protože jde směrem
klesající E), druhý krok nás oddálí ještě víc a tak dále, takže v lokálním
maximu neskončíme.
Gradientová metoda tedy skončí poblíž lokálního minima, které je kvůli
vlastnostem E i globální minimum, a tedy bod, ve kterém skončíme, bude
určovat parametry lineárního modelu s malou chybou.
Zbývá už poslední kousek skládačky: jak gradient E spočítáme?
Pokud bychom o E nevěděli nic, mohli bychom místo počítání gradientu zkusit
jenom o trošku pohnout každou složkou β a vybrat to drobné
pohnutí, které E nejvíc zmenší. To bude poměrně pomalé, ale jednoduché a
bude to fungovat na všechna E, co jsou spojitá, mají jediné lokální minimum,
které je zároveň i globální minimum a nemají inflexní body.
Gradient se dá pro naši definici chyby spočítat explicitně. Je to vektor
o (p+1) složkách a jeho i-tá složka se spočítá tímto průměrem přes
všechny trénovací vzorky:
∇E(β)
i=2 ·
∑
(x,y)∈S x
i (f
β(x) - y).
Poslední složka (odpovídající členu ϑ) se spočítá jako:
∇E(β)
(p+1)=2 ·
∑
(x,y)∈S (f
β(x) - y).
V obou rovnicích je fβ lineární model určený parametry β.
Bitevní plán: Začneme v libovolném (třeba nulovém) bodě
β0=(α→0,ϑ0). Spočítáme gradient, odečteme jeho
γ-násobek a opakujeme, dokud gradient není malý vektor nebo nás to
nepřestane bavit. Uložíme výsledný model.
Je zaručeno, že gradientová metoda minimalizuje spojité funkce, které mají
jediné globální a lokální minimum a nemají inflexní body.
Často se ale používá i na spojité funkce, které tuhle vlastnost nemají. Potom
může skončit v lokálním, ale ne nutně globálním optimu, nebo v inflexním bodě.
V praxi nám to ale často nevadí – i tak dává použitelně dobré
výsledky. Gradientové metodě také můžeme pomoct náhodnými restarty
– pustíme ji několikrát za sebou z různých náhodně zvolených β0. Dá se
pak doufat, že projdeme větší kus definičního oboru E, takže v nejlepším
nalezeném bodě budeme blíž globálnímu minimu.
Úkol 3 [6b]
Stáhněte si ze stránky seriálu
dataset o spotřebě benzínu v USA.
Soubor má 5 sloupců dat oddělených čárkami.
Každý řádek jsou data z jednoho státu. První sloupec je vybíraná daň z benzínu
v centech na galon, druhý je průměrná mzda v dolarech, třetí délka dálnic ve státu
v mílích, čtvrtý je poměr obyvatel s řidičským průkazem a pátý je roční spotřeba
benzínu ve státě v milionech galonů.
Naprogramujte lineární regresi a pomocí ní odvoďte vzorec na předpovídání
spotřeby benzínu podle ostatních hodnot. Data nemusíte dělit na testovací a
trénovací množinu. Pro nás fungovalo dobře začít v nulových parametrech a pak
provést 100 000 iterací gradientové metody s γ=10-8. Pošlete svůj
zdrojový kód a nalezenou střední kvadratickou odchylku na celém datasetu.
Zkuste ji mít menší než 21 800.
Algoritmus K nejbližších sousedů
Algoritmus K nejbližších sousedů (anglicky K-nearest neighbors nebo
KNN) je založený na jednoduché myšlence: když chceme podle mojí výšky a
obvodu pasu předpovědět mou hmotnost, odhadneme ji podle lidí, kteří jsou mi
podobní výškou a obvodem pasu.
Model si bude pamatovat všechna trénovací data a jeho jediný parametr je
přirozené číslo K. Když nám přijde nový vstup x, najdeme ve trénovacích
datech K vzorků, které jsou mu nejbližší. Podíváme se na známé výstupy pro
nejbližší sousedy, nějak je zagregujeme a výsledek vrátíme.
Konkrétní použití se liší podle toho, jak nadefinujeme, že je vstup x
„blízký“ k nějakému trénovacímu vzorku, a podle toho, jak z výstupů na
nejbližších sousedech vyrobíme předpověď pro neznámý vstup.
Blízkost se může definovat třeba podle malé euklidovské vzdálenosti
Euklidovská vzdálenost se
hodí na numerické příznaky. Pokud ji ale použijeme, je potřeba dát si pozor
na to, aby rozdíly v příznacích byly stejně významné.
Co tím myslím? Vzpomeňme si na příklad s předpovídáním hmotnosti a podívejme se
na tři vzorky s těmito vstupními příznaky:
| příznak |
i=1 | i=2 | i=3 |
|
x: výška v m |
1.93 | 1.92 | 1.4 |
| x: obvod pasu v cm |
83 | 86 | 82 |
Dobrovolník 1 se liší od dobrovolníka 2 jedním centimetrem výšky a třemi
centimetry obvodu pasu. Dobrovolník 1 se od dobrovolníka 3 liší 53 centimetry
výšky a jedním centimetrem obvodu pasu. Nemusíme být experti na antropologii,
abychom očekávali, že hmotnost dobrovolníka 1 bude podobnější hmotnosti
dobrovolníka 2 než dobrovolníka 3.
Rozhodli jsme se, že první složka (výška) bude číslo v metrech a druhá složka
(obvod pasu) v centimetrech. Když si spočítáme euklidovskou vzdálenost tak,
jak jsme si ji nadefinovali, dostaneme:
d(x(1),x(2))=(1.93 - 1.92)2 + (83 - 86)2 = 9.0001
d(x(1),x(3))=(1.93 - 1.4)2 + (83 - 82)2 = 1.2809
Dobrovolník 3 je tedy navzdory naší intuici dobrovolníkovi 1 mnohem
„euklidovsky blíž“ než dobrovolník 2. Je to tím, že jsme zvolili pro
příznaky taková měřítka, že změna ve výšce je mnohem podstatnější než numericky
stejně velká změna v obvodu pasu. Kdybychom tedy hledali blízké vzorky podle
euklidovské metriky, neodpovídalo by „blízké okolí“ našim představám.
Tohle se dá částečně řešit tím, že si vstupní data normalizujeme. Jeden
ze způsobů normalizace je spočítat pro každý příznak jeho minimum a maximum
na trénovací množině, pak všechny jeho hodnoty přeškálovat do intervalu
[0;1] a počítat euklidovské vzdálenosti na přeškálovaných příznacích. Stejné
přeškálování provedeme, když máme udělat předpověď pro nový vstup.
Když jsou všechny naše příznaky diskrétní, můžeme definovat blízkost
podle takzvané Hammingovy vzdálenosti. Hammingova vzdálenost dvou vektorů je
počet jejich složek, které se liší.
Zbývá agregace předpovědí z okolí. Pro regresi je nejjednodušší vzít výstupy
z nejbližších sousedů a vrátit jejich průměr. Pro klasifikaci můžeme
třeba vrátit tu kategorii, která má mezi K sousedy nejvíce hlasů (a když
jich nejvíce hlasů dostalo několik, vybereme z takových třeba tu první).
Počítání průměru na kategoriích totiž nemusí být dobře definovaná operace.
Úkol 4 [6b]
Stáhněte si ze stránky seriálu
dataset o kvalitě bílého vína.
Obsahuje 12 sloupečků oddělených čárkami. První řádek popisuje význam sloupců.
Prvních 11 sloupců obsahuje různé chemické vlastnosti vína a poslední jeho
kvalitu mezi 1 a 10, kterou se naučíme předpovídat.
Naprogramujte algoritmus K nejbližších sousedů s normalizací příznaků
a euklidovskou vzdáleností. Z kvality od K sousedů vytvářejte předpověď
prostým aritmetickým průměrem.
Rozdělte dataset na trénovací, validační a testovací množinu v poměru
60 %/20 %/20 %.
Měřte střední kvadratickou chybu na trénovací a validační množině v závislosti
na K. Zkuste všechna K od 1 do 40.
Jak na K záleží chyba na trénovací množině? Jak na K záleží chyba
na validační množině? Proč?
Vyberte nejslibněji vypadající K a pomocí testovací množiny odhadněte,
jaká bude skutečná accuracy vašeho modelu.
Tahle úloha nejspíš poběží celkem dlouho. Jestli jí chcete pomoct, můžete
zkusit využít více jader procesoru. K řešení přibalte svůj program a výsledky.
Opisování od evoluce
Nejúspěšnější nám známý učenlivý systém byl vytvořen přibližně čtyřmi
miliardami let evoluce. Inspirováni jeho architekturou jsme vymysleli
mnoho forem umělých neuronových sítí. Obzvlášť v posledních několika
letech jsme díky několika novým trikům a rychlejším paralelním počítačům
dosáhli úžasných výsledků, mimo jiné ve zpracování obrazu a zvuku, ale třeba
i přirozeného jazyka.
Informace v lidském lidským mozku posílají elektrické a chemické signály.
Domníváme se, že nejdůležitější „výpočetní jednotkou“ je neuron.
Většina neuronů má nějaké „vstupní kanály“, kterým se říká dendrity, a jeden „výstup“ – axon. Dendrity tvoří jakousi
„stromovitou strukturu“, která sahá řádově stovky mikrometrů od těla neuronu.
Zatímco dendritický strom některých neuronů má až tisíc větví, některé neurony
jich mají pouhé jednotky.
Délka některých lidských axonů dosahuje až 1 metru. Každý neuron má sice
nejvýše jeden axon, ale ten se může mnohonásobně větvit a posílat jeho signály
až stovkám jiných neuronů.
Elektrické signály v nervovém systému jsou kódované pulzně. Neuron „sbírá“
signály od svých vstupů a pokud se v neuronu nahromadí za určitou dobu
dostatečné množství potenciálu, „vystřelí“ signál na výstupu.
Spojením mezi neurony se říká synapse. Některé synapse jsou excitační
a některé jsou inhibiční. Signály poslané po excitačních synapsích
„zvyšuje vnitřní potenciál“ cílového neuronu, zatímco inhibice mu „brání
vystřelit“.
Možná překvapivě se informace v mozku šíří relativně pomalu. V závislosti
na typu signálu jsou to řádově jednotky až stovky metrů za
sekundu (Například signály od receptorů bolesti nebo teploty se šíří
rychlostí asi 0.5 až 2 m/s. Oproti tomu signály od proprioreceptorů –
detektorů relativní pozice jednotlivých částí těla – se šíří rychlostí mezi 80
a 120 m/s. Lidský mozek obecně funguje mnohem pomaleji než sériové
počítače. Procesy v něm jsou však vysoce paralelizované.).
Systému neuronových spojení v mozku se souhrnně říká konektom.
Můžeme si jej představit velmi zjednodušeně jako poněkud gigantický orientovaný
graf, jehož vrcholy tvoří jednotlivé neurony. Hrany reprezentují spojení a
vedou směrem, jakým se přenáší signály: od neuronu, který je vypálí,
do neuronu, který je má na vstupu. Kromě toho, že hrany mohou reprezentovat
excitační nebo inhibiční spojení, existuje samozřejmě velmi mnoho dalších
parametrů, které mají vliv na zpracování signálů.
Učení probíhá změnou vlastností konektomu, například přidáváním nových
synapsí nebo změnami parametrů těch synapsí, co už existují. Když synapticky
spojené neurony pálí společně, jejich spojení se posiluje.
Umělé neuronové sítě modelují skutečnost s různou úrovní detailu a mají mnoho
různých aplikací, podle kterých se odvíjí jejich architektura. Začneme od
nejjednoduššího modelu, který dělá něco užitečného.
Umělý neuron
Namísto posílání pulzních signálů budeme reprezentovat informaci pomocí čísel.
Umělý neuron je pro nás jednotka, která má n číselných vstupů x1, … xn a jeden výstup y.
Neuron bude ze svých vstupů počítat potenciál ξ. Některé vstupy budou
k potenciálu přispívat pozitivně, některé negativně. Výstup y bude záviset na
potenciálu podle takzvané aktivační funkce, značené a: y=a(ξ).
Směr příspěvku, tedy míra excitace nebo inhibice, bude pro každý vstup
jiná a bude určená takzvanou vahou (weight).
Váha i-tého vstupu se značí wi.
Standardně se potenciál počítá jako součet vážených příspěvků všech vstupů.
K tomuto součtu se také přidá takzvaný bias
(český překlad by mohl být „předsudek“ nebo „sklon“) ϑ:
ξ=ϑ+ ∑i wi xi.
Aktivační funkce se používají různé. Vždy jsou definované na celém R,
omezené (většinou na [-1;1] nebo [0;1]) a rostoucí (respektive
neklesající). První model, který si ukážeme, bude vracet 1, pokud je
ξ≥ 0, a jindy -1 (tedy jeho aktivační funkce je funkce signum).
Perceptron
Takovému umělému neuronu se říká perceptron. Jeho výstup je 1, pokud
ϑ+ ∑i wi xi ≥ 0, a jindy -1. Jsou-li vstupy perceptronu dva, je
ϑ+ ∑i wi xi = 0 rovnice přímky ve dvou rozměrech. Perceptron
touhle přímkou rozděluje dvojrozměrný prostor vstupů na dvě poloroviny. V jedné
vrací 1 a ve druhé vrací -1. Přidáme-li další vstupy, analogicky perceptron
dělí n-rozměrný vstupní prostor na dva poloprostory.
Perceptron lze použít jako jednoduchý klasifikátor dvou kategorií, pro něž
bude jeho očekávaný výstup 1 a -1. Rozdělíme si vstupní příznaky trénovacích
dat do pozitivní kategorie P a do negativní kategorie N.
Ukážeme si algoritmus perceptronového učení, o kterém víme, že pokud jdou
kategorie P a N od sebe bez chyb rozdělit perceptronem (neboli
nějakou nadrovinou), pak náš algoritmus nakonec najde váhy nějakého takového
perceptronu.
Nejdříve ke všem vzorkům v P a N přidáme jako novou složku na
začátek jedničku. Tím pádem můžeme zapomenout na bias – stane se z něho nová
první váha. Vzorky „vylepšené“ o jedničky označíme jako P' a N'.
Potom sjednotíme vzorky do jedné množiny. N' mají být vzorky, pro které
∑i wi xi < 0, a to platí právě tehdy, když ∑i wi ·(-xi) >
0. Vyrobíme si množinu R, která se bude skládat z P' a
minus jedničkou vynásobených vektorů z N'. Perceptron, ve kterém jsou všechny vektory
v R v pozitivní polorovině, bude správně klasifikovat P' i N'.
Zinicializujeme perceptron libovolnými vahami, třeba nulovými. Učení probíhá
tak, že iterujeme přes množinu R a postupně perceptron učíme jednotlivé
vzorky x. Chceme po něm, aby na každém vzorku bylo ∑i wi xi
větší než 0.
Pokud na zkoumaném vzorku je ∑i wi xi > 0, je vzorek perceptronem
rozpoznaný správně, neděláme nic a jdeme na další vzorek. Pokud je suma menší
než 0, pak ke každé váze wi přičteme xi ·γ a jdeme se učit další
vzorek. γ je tady opět rychlost učení, konstanta mezi 0 a 1.
Pokud najdeme perceptron, který správně klasifikuje všechny vstupy, vrátíme ho.
Pokud jenom chceme dobrý perceptron, který ne nutně klasifikuje všechno dobře,
můžeme místo toho jenom běžet, dokud nám nedojde čas, a pak vrátit ten perceptron,
který dokázal klasifikovat nejvíc vzorků po sobě správně.
Úkol 5 [6b]
Stáhněte si ze stránky seriálu
dataset o kosatcích. Tento slavný „Iris dataset“ poprvé použil v 30. letech
významný biolog a statistik Ronald Fischer. Každý řádek reprezentuje
vlastnosti jednoho kosatce. První řádek popisuje význam sloupečků: první dva
jsou délky a šířky kališních lístků, další dva jsou délky a šířky okvětních
lístků. Máme za úkol předpovědět poslední sloupec – konkrétní druh kosatce:
setosa, versicolor, nebo virginica.
Zkuste naprogramovat rozpoznávání kosatců pomocí perceptronů.
Jeden perceptron dokáže od sebe rozpoznat jenom 2 třídy, budete muset být
kreativní.
Není jediné správné řešení – překvapte nás! Jakou zvládnete accuracy na
testovacích datech? Naše autorské řešení umí z 60 trénovacích vzorků
mít na zbytku datasetu 93.42 %.
Perceptrony jsou užitečné, ale pořád docela slabé – pokud mají kategorie
„složitou hranici“ a nejdou lineárně oddělit, potřebujeme na jejich naučení
našim modelům povolit složitější strukturu.
Zábavné věci se začnou dít třeba, když začneme neurony vrstvit do takzvaných
dopředných vrstevnatých neuronových sítí (feedforward neural networks).
První vrstva takové sítě jsou vstupní data. Druhá vrsta konzumuje výstup první
vrstvy jako svůj vstup. Sedí v ní kupříkladu 10 neuronů a každý z nich má
vlastní váhy a transformuje vstupy jiným způsobem. Výstupy druhé vrstvy
jsou vstupy pro třetí vrstvu, a tak dále až do výstupní vrstvy. Informace se
šíří jenom z nižších vrstev do vyšších. Vyšší vrstvy jsou schopné počítat
složitější a složitější transformace vstupních dat.
Michal Pokorný
Řešení
 28-4-1 Sledování telefonů (9 bodů)
28-4-1 Sledování telefonů (9 bodů)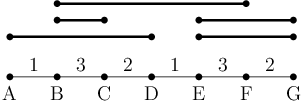
 Lehčí varianta (za 5 bodů): Řešte za předpokladu, že se počty zachycených hovorů
na libovolných dvou sousedních spojích liší maximálně o 10.
Lehčí varianta (za 5 bodů): Řešte za předpokladu, že se počty zachycených hovorů
na libovolných dvou sousedních spojích liší maximálně o 10.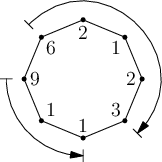
 28-4-3 Řazení životních hodnot (10 bodů)
28-4-3 Řazení životních hodnot (10 bodů) 28-4-4 Podivuhodný obraz (12 bodů)
28-4-4 Podivuhodný obraz (12 bodů) V domě visí podivuhodný obraz. Je na něm nakreslených
V domě visí podivuhodný obraz. Je na něm nakreslených 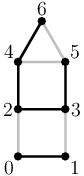
 28-4-8 Strojové učení (20 bodů)
28-4-8 Strojové učení (20 bodů)