Třetí série dvacátého devátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 29-3-1: Verbování
- 29-3-2: Trpasličí závaží
- 29-3-3: Skřetí věže
- 29-3-4: Mezi hlídkami
- 29-3-5: Dračí zámek
- 29-3-6: Obrazec pro draka
- 29-3-7: Stromoví předci
 29-3-1 Verbování (Zadání)
29-3-1 Verbování (Zadání)
Představme si, že jsme u města Leyfast a procházíme očíslované domy. V každém z domů máme několik možností, jak se rozhodnout. Abychom nalezli nejlepší řešení, můžeme zkusit každou možnou kombinaci rozhodnutí a vybrat tu nejvýhodnější, ale to by trvalo příliš dlouho.
Můžeme také zkusit vybírat další krok hladově, neboli vybírat možnost neporušující pravidla, která nám lokálně (pro tento dům) dá nejlepší výsledek. To bude sice rychlé, ale nedostaneme takhle správnou odpověď. Zkuste si to na nějakých vstupech, k rozbití tohoto postupu stačí již ukázkový vstup ze zadání.
Problémem hladového řešení je, že nijak nerespektuje to, že volba v i-tém domě ovlivňuje možné volby v okolních domech. Připomeňme si, co můžeme v domě udělat. Pokud skrz domy půjdeme odzadu, tak můžeme:
- Naverbovat vojáka, pokud jsme tak neučinili v předchozím a neučiníme-li tak v ani následujícím domě.
- Vzít zbraně, pak musíme nutně naverbovat vojáka v následujícím domě.
- Nevzít zbraně ani nenaverbovat vojáka.
Volba, která ovlivňuje výběr v okolních domech, je verbování. Pokud se zkusíme podívat na problém omezený jen na prvních i domů, tak by nás pro další rozhodování mohlo zajímat, jaké nejvyšší bojeschopnosti umíme dosáhnout, pokud si v i-tém domě dovolíme naverbovat vojáka a pokud si zde vojáka nepovolíme naverbovat.
Postavíme si pro to rekurzivní funkci B(i, (true|false)), která bude počítat přesně toto. Pokud se nám povede ji spočítat, tak celkovou maximální bojeschopnost získáme zavoláním B(N, true).
Teď si budeme muset sestavit funkci (pro připomenutí, v Zi je zisk bojeschopnosti při braní zbraní z i-tého domu, v Vi to samé, ale pro verbování z i-tého domu).
- Pro i ≤ 0 bude mít funkce vždy hodnotu 0.
- B(i,false) bude maximum z:
- Zi + Vi-1 + B(i-2, false) (budeme brát zbraně, což vynutí verbování v i-1; lze použít jen pro i > 1)
- B(i-1, true) (nebudeme dělat nic)
- B(i,true) bude maximum z B(i,false) a navíc:
- Vi + B(i-1, false) (budeme verbovat)
Takovouto funkci lze jednoduše naprogramovat. Horší je exponenciální časová složitost způsobená větvením výpočtu v každém domu. Naštěstí funkce, kterou jsme právě definovali, závisí pouze na dvou parametrech: i a verbovat.
Výsledky volání si tak můžeme ukládat do tabulky velikosti 2N. Při opakovaném zavolání pak stačí vrátit už dříve spočítaný výsledek. Spočítáme tedy nejvýše 2N hodnot funkce B, proto dostáváme lineární složitost vzhledem k počtu hodnot na vstupu.
Zbývá domyslet, jak navíc zjistit jeden z plánů verbování nabývající hodnoty B(N, true). Například můžeme spustit znovu trochu modifikovanou funkci počítající B, která bude nyní vracet odkaz na i-tý prvek spojového seznamu, který reprezentuje jeden ze znaků (z,v,-). Všimněme si, že takto použijeme jen N položek seznamu, protože už máme spočítány hodnoty B a v každém kroku tak voláme pouze jednou naši modifikovanou funkci.
Na trochu (ale jen konstantně) elegantnější řešení s nahrazením spojového seznamu řetězcem se můžete podívat do vzorového programu v C++.

 29-3-2 Trpasličí závaží (Zadání)
29-3-2 Trpasličí závaží (Zadání)
K porovnávání váhy sad závaží a protizávaží se dalo použít několik různých postupů. Jedním z nich bylo převést zápis na takový, který bude obsahovat jen jedničky a nuly, a tento pak porovnat jako se porovnávají binární čísla. Druhou možností je porovnat zápisy v této „rozšířené dvojkové soustavě“ přímo.
Za chvíli si ukážeme obě možnosti, nejdříve ale proveďme pozorování. Podobně jako v klasické dvojkové soustavě má každá pozice dvojnásobnou hodnotu než pozice předchozí. Když si budeme postupně sčítat hodnoty na dalších pozicích (za nějakou pozicí s hodnotou x), tak nejdříve dostaneme polovinu x, z další pozice čtvrtinu (neboli polovinu té zbývající poloviny do x) a tak dále. Každá další pozice nám součet více přiblíží k hodnotě x, ale nikdy ho nepřesáhne. Protože pozic v binárním čísle je konečně mnoho, přiblíží se na jedničku a víc už ne – matematici by řekli:
| n |
| i=0 |
Takže pokud bude nejlevější nenulová pozice čísla zapsaného v této soustavě záporná, tak i kdyby všechny ostatní pozici již byly kladné, dostaneme nejvýše -1 (a tedy celé číslo bude záporné). A naopak, pokud bude kladná, tak číslo bude kladné.
Podle tohoto můžeme udělat první porovnání a pokud mají nejvyšší pozice obou porovnávaných čísel rozdílná znaménka, můžeme rovnou oznámit výsledek a končíme. Dál tedy budeme zabývat jen případy, kdy jsou znaménka na nejvyšších pozicích stejná.
Další triviální pozorování je, že překlopením všech znamének na opačná vlastně jen změníme znaménko celého čísla.
Převod do dvojkové soustavy
Pro jednoduchost budeme popisovat převod pro čísla, jejichž nejvyšší nenulová pozice je kladná (kdyžtak si je podle předchozího pozorování překlopíme a zapamatujeme si, že je číslo vlastně záporné).
Budeme se chtít zbavit všech výskytů -1 v zápisu čísla. Všimněme si, že následující zápisy můžeme bez změny hodnoty převádět:
- (1,-1) →(0,1)
- (0,-1) →(-1,1)
Můžeme tedy zahájit převod od nejmenšího řádu zprava a takto si mínus jedničky průběžně eliminovat, nebo si je posílat dál doleva. Máme ale jednu situaci, kterou jsme si nepopsali – co když se nám vedle sebe objeví dvě mínus jedničky?
Na chvíli si povolíme použít i hodnotu -2 a podívejme se, co se nám při přičtení dvojice (-1,+2) může stát:
- (-1,-1) →(-2,1)
- (-1,-2) →(-2,0)
- (0,-2) →(-1,0)
- (1,-2) →(0,0)
Převod tedy umíme udělat lineárním průchodem číslem od nejmenšího řádu k největšímu a eliminováním mínus jedniček pomocí přičítání vzoru (-1,+2). Pokud takto převedeme obě čísla, už je snadno porovnáme binárně (průchodem od největšího řádu a hledáním první pozice, kde se liší).
Porovnání odečtením
Pokud vám převod do normální dvojkové soustavy přijde jako nehezký trik, dá se porovnání udělat i odečtením jednoho čísla od druhého. Podle toho, jestli nám výsledek vyjde kladný, nebo záporný (což poznáme podle znaménka nejvyšší jedničky), určíme snadno, které číslo je větší.
Odečítání můžeme dělat klasickým školním postupem od nejmenšího řádu. Pokud nám výsledek odečtení vyjde 1, 0 nebo -1, je vše v pořádku. Pokud nám vyjde menší, než -1, tak musíme udělat převod -1 do vyššího řádu (a k tomu současnému přičteme +2, vlastně opět aplikujeme vzor (-1,+2)). Pokud nám vyjde naopak větší než 1, přičteme -2 a pošleme převod 1 (tedy použijeme vzor (+1,-2)).
Pojďme se podívat na průběh výpočtu třeba čísla 1,-1,-1, od kterého odečteme číslo 1,1 (neboli 1-3 = -2). V prvním kroku nám na poslední pozici výsledku vznikne -2, což převedeme na 0 a do vyššího řádu pošleme -1. Na druhé pozici dostaneme -3 (i s převodem), což převedeme na -1 a do vyššího řádu pošleme -1. A nakonec na nejvyšší pozici dostaneme 1-1=0, čímž získáme správný výsledek 0,-1,0.
Tento postup zabere také lineární čas vzhledem k velikosti vstupních čísel. Na oba postupy se můžete podívat v přiloženém programu.
 29-3-3 Skřetí věže (Zadání)
29-3-3 Skřetí věže (Zadání)
Mnoho z vás přišlo s nápadem zkoušet různé přímky a ověřit, jestli se náhodou nejedná o hledanou osu. Všechny možné přímky však určitě vyzkoušet nemůžeme, těch je nekonečně mnoho. Které přímky tedy připadají v úvahu?
Využijeme toho, že každý bod musí mít při osové souměrnosti svůj obraz. Očíslujeme si tedy body postupně P0, P1, …, PN-1. Budeme nejprve předpokládat, že bod P0 se zobrazí na nějaký jiný bod a ne sám na sebe.
Všimněte si, že pokud bychom věděli, na který bod se P0 zobrazí, je osa souměrnosti jednoznačně určená: musí to být osa úsečky spojující P0 s jeho obrazem. My samozřejmě nevíme, na který bod se P0 zobrazí, ale můžeme vyzkoušet všechny možnosti. Tím získáme N-1 přímek, mezi nimiž se určitě hledaná osa nachází (za předpokladu, že nějaká osa existuje a bod P0 není obrazem sebe sama).
Rozmyslíme si ještě případ, kdy P0 je sám sobě obrazem a nachází se tedy přímo na ose. Nejjednodušší je vzít místo P0 bod P1 a k němu stejným postupem zkoušet body P2 až PN-1. Takto vyřešíme případy, kdy alespoň jeden z bodů P0 a P1 neleží na ose. Pokud by oba ležely na ose, je osou přímka P0P1 – tu také přidáme do seznamu kandidátů.
Tímto postupem jsme tedy získali 2N-2 přímek, mezi nimiž se určitě osa nachází (existuje-li). Stačí pro každou z přímek ověřit, jestli osou skutečně je, tj. jestli má každý bod svůj obraz.
Nejprve si pro každý bod spočítáme, kam by se při dané ose zobrazil. Pokud bod leží přímo na ose, je sám sobě obrazem. Pokud na ose není, chce to trochu počítání, ale nic náročného. Vezmeme přímku procházející daným bodem, která je kolmá na osu, a spočítáme její průsečík s osou. Tento průsečík se musí nacházet ve středu úsečky spojující daný bod a obraz, takže souřadnice obrazu se už jednoduše dopočítají.
Pro každý bod tedy víme, kam se zobrazí. Teď už stačí zkontrolovat, že v místě obrazu leží nějaký jiný bod – v opačném případě zkoumaná přímka osou není. Pokud bychom při kontrolování obrazu pokaždé procházeli všechny body, bude nám kontrola jednoho obrazu trvat O(N), kontrola všech obrazů O(N2) a prozkoumání všech 2N-2 přímek O(N3).
Tento postup lze zrychlit vhodným setříděním bodů. Pro každou potenciální osu body setřídíme podle polohy jejich průmětu na osu (to je pata kolmice k ose, na níž leží daný bod). Všimněte si, že tento průmět jsme už spočítali při hledání souřadnic obrazu. Můžeme využít toho, že pokud má být bod Pk obrazem Pℓ, budou souřadnice jejich průmětů na osu stejné.
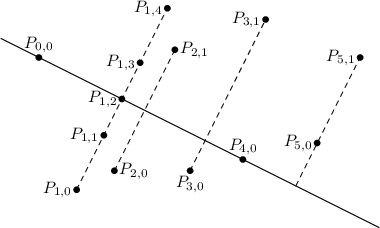
Pokud máme tedy takto setříděné body, můžeme je brát postupně. Vždy vezmeme všechny body se stejnými souřadnicemi průmětu a uložíme je do dalšího pole. Toto další pole opět setřídíme, tentokrát podle pozice na přímce, na které se všechny nacházejí (to je nějaká přímka kolmá k ose). Je zřejmé, že první bod v tomto menším seznamu musí být obrazem posledního, druhý předposledního atd. Pokud si nějaká tato dvojice není navzájem obrazem, některý bod z dvojice nemá obraz a zkoumaná přímka není osou.
Původní setřídění bodů zvládneme v čase O(N log N), třídění menších seznamů stihneme ještě rychleji. Kontrolu po setřídění stihneme v lineárním čase. Jelikož zkoumaných přímek je stále lineárně, činí celková složitost O(N2 log N).
Celý tento algoritmus můžeme ještě zrychlit použitím hešovací tabulky. Jednoduše si souřadnice všech bodů do jedné takové tabulky uložíme. Pak pro každý bod spočítáme souřadnice jeho obrazu podle dané osy a podíváme se do tabulky, jestli se tam bod s takovými souřadnicemi nachází. Jelikož zjištění existence v hešovací tabulce proběhne v průměrně konstantním čase, získáme ověření osy v čase průměrně lineárním. Celkově tedy v průměrném čase O(N2). Toto řešení už stačilo na získání plného počtu bodů.
Těžiště na pomoc
Pojďme se ale ještě podívat na řešení jiného typu, třeba povede k ještě lepším výsledkům. Někteří z vás chytře využili toho, že těžiště bodů se jistě nachází na ose souměrnosti. Proč tomu tak vlastně je? Těžiště můžeme počítat postupně, tedy tak, že si body rozdělíme do skupinek, spočítáme těžiště skupinek a pak spočítáme těžiště těchto těžišť (každé z těchto těžišť ještě vážíme počtem bodů z příslušné skupinky).
Můžeme tedy vzít body po dvojicích – vždy si vezmeme bod a jeho obraz (body, co leží přímo na ose, necháme samostatně). Těžiště každé této dvojice (tj. střed příslušné úsečky) se nachází přesně na ose. Těžiště samostatného bodu je přímo tento bod. Každé takto spočítané těžiště se nachází na ose, tedy i těžiště těchto těžišť – jakkoli vážené – se bude opět nacházet na ose. Tím pádem tam bude ležet i těžiště původních bodů.
Poznamenáme ještě, že těžiště dokážeme spočítat v lineárním čase. Stačí spočítat průměr x-ových a průměr y-ových souřadnic jednotlivých bodů. Výsledkem jsou souřadnice těžiště.
Takto získáme jeden bod osy, musíme ještě přijít na druhý. Jeden způsob je opět zkoušet středy úseček P0Pk pro ostatní k. Tento způsob je zdánlivě lepší oproti předchozímu v tom, že můžeme poměrně rychle odmítat přímky, které nejsou osami. Protože aby se P0 zobrazilo na Pk, musí být přímka P0Pk se středem S kolmá na osu TS (T je těžiště) a navíc musí TS protínat P0Pk ve středu úsečky P0Pk. Všechno toto dokážeme zkontrolovat v konstantním čase a rychle tak odmítnout spoustu potenciálních os.
Když však všechny tyto rychlé kontroly uspějí, musíme opět ověřit, jestli je daná přímka skutečně osou. To můžeme provést jedním ze způsobů popsaným v předchozí části.
Nicméně v obecném případě jsme si moc nepomohli. Jako účinný protipříklad se ukáže množina vrcholů pravidelného n-úhelníku sjednocená s množinou bodů rovnostranného trojúhelníku se stejným těžištěm, která způsobí, že celá množina osově symetrická není.
Sami si můžete vyzkoušet, že pokud budou vrcholy z trojúhelníku brány až jako poslední v pořadí, skutečně jsme si, co se rychlosti týká, oproti předchozímu postupu vůbec nepomohli – stále budeme muset zkoušet O(N) os a žádnou se nám nepodaří odmítnout rychlým způsobem. Každou osu budeme muset ověřit pomalým způsobem, celkově jsme tedy stále na složitosti O(N2). Pro jiné přístupy je ještě horší případ, kdy všechny body z trojúhelníku i z n-úhelníku mají od těžiště stejnou vzdálenost.
Zdá se, že najít těžiště nám vlastně vůbec nepomohlo. Kdepak, opak je pravdou. Na následujících řádcích si ukážeme ještě rychlejší řešení, které se právě o těžiště opírá.
Jde to ještě rychleji
Odrazíme se od souřadnic těžiště. Všechny body posuneme tak, aby těžiště bylo na počátku souřadnicového systému a nadále budeme počítat s těmito upravenými souřadnicemi. Pak víme, že osa souměrnosti, pokud existuje, bude procházet počátkem (tj. těžištěm).
Dále budeme pracovat s takzvanými polárními souřadnicemi, tj. místo x-ové a y-ové souřadnice budeme mít u každého bodu úhel, který svírá x-ová osa s přímkou spojující daný bod s počátkem (těžištěm), a vzdálenost od počátku.
Potom si seřadíme body podle úhlu (prozatím budeme předpokládat, že žádné dva body nemají stejný úhel). Máme tedy u každého bodu Pi úhel φi. V tomto setříděném pořadí budeme nadále vrcholy zpracovávat, ale ukáže se, že důležité pro nás bude pamatovat si rozdíl úhlu oproti předchozímu vrcholu. Tedy pro každý vrchol spočítáme δi = φi - φi-1 a pro nultý vrchol δ0 = φ0 + 360 °- φN-1. Všimněte si, že součet přes všechna δi nám dá 360 °.
Pokud vzdálenost jednotlivých bodů budeme značit pomocí ri, můžeme teď úhly a vzdálenosti zapsat do řetězce s = δ0r0δ1r1… δN-1rN-1. Tedy jednotlivé ri a δi budeme chápat jako jednotlivé znaky řetězce. Všimněte si, že z tohoto řetězce lze zpětně zrekonstruovat původní rozložení bodů (až na rotaci okolo středu, která neovlivňuje osovou souměrnost). Prostě se vždy otočíme o daný úhel δi a nakreslíme bod ve vzdálenosti ri od počátku.
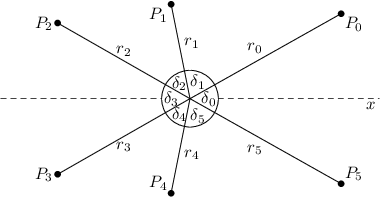
Představme si na chvíli, že osa x je hledanou osou souměrnosti. Uvažujme případ, kdy žádný bod neleží na pravé straně této osy (tedy neexistuje bod s φi = 0). Pak není těžké si představit, že některé úhly a vzdálenosti si musí odpovídat. Konkrétně r0 = rN-1, δ1 = δN-1, r1 = rN-2, δ2 = δN-2 atd. Pro případ, kdy bod leží na pravé straně osy x dostaneme podobné rovnosti, jen trochu posunuté, δ0 = δN-1, r1 = rN-1 atd.
Každopádně si všimněte, že oba případy znamenají, že řetězec s je skoropalindrom (palindrom je řetězec, který se stejně čte zepředu i zezadu, tedy že první znak je stejný jako poslední, druhý je stejný jako předposlední atd.). Přesněji řečeno v prvním případě dostaneme palindrom, když za s připíšeme první znak s (tj. δ0), ve druhém, když před s připíšeme jeho poslední znak (tedy rN-1).
Bohužel nemáme zaručeno, že osou souměrnosti bude osa x. Takže musíme řetězec s vhodně zrotovat, tj. opakovaně brát poslední znak řetězce a dát jej na první místo. Všimněte si, že pokud zrotujeme do nějakého stavu
a na konec zkopírujeme první znak (rk), výsledek je palindromem právě tehdy, když osa prochází bodem rk. Analogicky pokud rotací dostaneme řetězec
a opět zkopírujeme δk, výsledek je palindromem právě tehdy, když osa prochází středem úsečky mezi body Pk-1 a Pk.
Uvědomme si, že to jsou jediné možnosti, kde osa souměrnosti může ležet. Máme-li totiž těžiště T (nebo jiný libovolný bod na ose souměrnosti), bod A a jeho obraz A', tak úhel mezi přímkou TA a osou souměrnosti musí být stejný jako mezi osou a přímkou TA'. Představme si, že by tedy osa dělila nějaký úhel δk na úhly δk' a δk''. Nechť je δk' ten menší z nich a bod při tomto úhlu (Pk nebo Pk-1) označíme K. Bod K se musí zobrazit na jiný bod, který dává s osou úhel δk' (resp. 360 °- δk', podle toho, jak se na to díváte), ale všechny ostatní body dávají úhel větší (resp. menší), K tedy nemá obraz a zkoumaná přímka není osa.
Stačí vyzkoušet všechny tyto rotace a podívat se zda nejsou skoropalindromem. Pokud si budeme uchovávat řetězec ve spojovém seznamu s ukazatelem na začátek i konec, další rotaci vytvoříme v konstantním čase, stačí odebrat prvek z konce seznamu a dát jej na začátek. Samotná kontrola, jestli je řetězec skoropalindromem, bude v lineárním čase. Stačí zkontrolovat jestli je první prvek shodný s předposledním, druhý s předpředposledním atd. To zvládneme pomocí dvou ukazatelů, které vždy posuneme o jednu pozici.
Nicméně to opět vypadá, že jsme si vůbec nepomohli. Jednu rotaci zkontrolujeme v čase O(N), ale rotací je také O(N), dohromady dostaneme opět O(N2). Nicméně častým trikem, když hledáme vhodnou rotaci, je negenerovat nové a nové rotace, nýbrž řetězec zkopírovat dvakrát za sebe. Zkusme to také.
Původně jsme hledali rotaci s palindromem délky 2N-1 (nezapomínejme, že N je počet bodů, délka s je tedy 2N), stejně tak můžeme hledat palindrom délky 2N-1 ve zdvojeném řetězci. To můžeme udělat tak, že najdeme nejdelší palindrom liché délky, pokud je delší než 2N-1, můžeme jej jednoduše zkrátit (odebíráním vždy dvojicí znaků z kraje) na tuto délku. A jak najít nejdelší palindrom? Na to se podíváme spolu v páté sérii. Zatím jen prozradíme, že to zvládneme v lineárním čase.
Už jsme téměř na konci, ale nesmíme zapomenout ještě na jednu věc. Na začátku tohoto řešení jsme předpokládali, že žádné dva body nebudou mít přiřazený stejný úhel φi.
S tím se už dá celkem snadno vypořádat. Trochu upravíme konstrukci řetězce s. Když budeme mít několik bodů stejný úhel, napíšeme jejich vzdálenosti do tohoto řetězce hned za sebou v setříděném pořadí. Protože ale potřebujeme, aby se sekvence bodů se stejným úhlem četla stejně popředu i pozpátku (abychom mohli problém převést na hledání palindromu), tak ji hned za ni zapíšeme znova, v opačném pořadí. Náš řetězec může vypadat například takto: δ0r0r1r2r2r1r0δ3r3r3δ4…
Odpovídajícím způsobem upravíme i délku hledaného palindromu. Ta je 2N+A, kde N je počet bodů a A je počet nenulových δi.
Pojďme si to shrnout a podívat se na výslednou složitost. Posunout body podle těžiště, stejně tak spočítat polární souřadnice zvládneme v lineárním čase. Setříděním bodů podle úhlů strávíme O(N log N). Zkonstruovat a zdvojit řetězec opět zvládneme lineárně a konečně jsme slíbili, že nalezení samotného palindromu jde také rychle. Celkově jsme se tedy konečně dostali na časovou složitost O(N log N).
 29-3-4 Mezi hlídkami (Zadání)
29-3-4 Mezi hlídkami (Zadání)
Ze všeho nejdříve úlohu převedeme na variantu, kde je zakázáno vstupovat pouze na políčka s hlídkou, ale na sousední šlápnout můžete. Uděláme to tak, že přidáme „virtuální“ hlídku na všechna pole sousedící s hlídkami ze zadání. Odpověď pro takto upravenou úlohu a vstup bude stejná jako pro původní zadání.
Jednou z možností, jak se úloha dala řešit, bylo si na začátku najít pomocí prohledávání do šířky nejkratší cesty mezi všemi dvojicemi políček. Při odpovídání na dotaz už budeme mít délku nejkratší cesty předpočítanou a můžeme ji jen vrátit.
Protože počítáme cesty na poli velikosti N×M políček, zabere nám vyhledání nejkratších cest z jednoho políčka do všech ostatních čas O(NM) (jedno prohledávání do šířky). Jelikož potřebujeme počítat vzdálenost mezi všemi dvojicemi políček, musíme prohledávání spustit pro každé políčko samostatně, což zabere O((NM)2) času a O((NM)2) paměti. To není příliš rychlé, zkusíme to vylepšit.
Rychlejší postup
Můžeme si všimnout, že vzhledem k malému počtu hlídek nejkratší cesta půjde většinu času po části pláně, kde žádné hlídky nejsou. Toho jde využít a dosáhnout tak lepší časové i paměťové složitosti. Dál v řešení budeme pracovat se souřadnicemi startu xs,ys a souřadnicemi cíle xc,yc.
Řešení si rozdělíme na dva případy – buď neexistuje hlídka, která je v obdélníku definovaném startem a cílem, a délka nejkratší cesty je tedy |xs-xc|+|ys-yc|, nebo nám po cestě nějaká hlídka bude překážet a budeme to muset vyřešit. Tyto dva případy také musíme být schopni odlišit, což vyřešíme v poslední části řešení.
Chtěli bychom si předpočítat nejkratší cestu mezi každými dvěma vrcholy, jenže to by trvalo příliš dlouho. Všimneme si ale, že ve sloupcích a řádcích, kde není hlídka, se „nic neděje“. Pokud je takových řádků nebo sloupců více vedle sebe, tak vždy všechny sloučíme (zkontrahujeme) do jednoho a poznamenáme si ke každému políčku, kolika políčkům odpovídá ve vertikálním a horizontálním směru. Jednotlivá zkontrahovaná políčka tak mohou odpovídat i docela velkých obdélníkům v původní pláni. Nejkratší cesty si pak předpočítáme až na této upravené pláni.
Při slučování si u každého políčka z původní pláně navíc zaznamenáme, kde je jeho „sloučená verze“ v kontrahované pláni. To se nám bude později hodit a takto se k této informaci dostaneme v konstantním čase.
Na této kontrahované pláni budeme chtít hledat nejkratší cesty. Může se zdát, že po úpravě, kdy některá políčka reprezentují větší vzdálenosti, nebude běžné prohledávání do šířky stačit, ale můžeme si rozmyslet, že díky kontrahování vždy celých řádků a sloupců bude i obyčejné prohledávání do šířky stále dostávat políčka ve správném pořadí – takové prohledávání do šířky totiž přiřadí políčkům stejná ohodnocení, jako kdybychom ho spustili na původní pláni. Nad tímto prohledáváním do šířky také můžeme přemýšlet jako nad Dijkstrovým algoritmem, který namísto haldy používá frontu.
Protože hlídek bylo k, tak takto upravená pláň má rozměry O(k2) (mezi sousedními hlídkami je maximálně jeden zkontrahovaný sloupec nebo řádek) a předpočítat si všechny nejkratší cesty tedy bude trvat O(k4).
Potřebujeme ještě umět zjistit, zda je v obdélníku definovaném startem a cílem hlídka. To můžeme udělat jednoduše pomocí dvoudimenzionálních prefixových součtů (o nich si můžete přečíst třeba v naší kuchařce základních algoritmů). Hlídky budeme považovat za jedničky a prázdná políčka za nuly. V daném obdélníku pak bude hlídka právě tehdy, když je v něm nenulový součet.
Dotaz pak bude vypadat následovně: Pokud mezi políčky není žádná hlídka, délka nejkratší cesty je |xs-xc|+|ys-yc|. Pokud mezi nimi hlídka je, využijeme naší kontrahované pláně, kde máme pro každou dvojici políček předpočítanou nejkratší cestu
Drobnou nesnází je, že start (nebo cíl) mohou ležet uvnitř nějakého kontrahovaného obdélníku. Můžeme si rozmyslet, že část cesty, která je v tomto obdélníku, může jít libovolnou nejkratší cestou do rohu nejbližšího k cíli (respektive startu), tuto část cesty spočítáme jako v případě výše.
A dál už pak vyhledáváme jen ve zkontrahované pláni, respektive v předpočítané datové struktuře délek cest mezi dvojicí zkontrahovaných políček.
Předpočítání kontrahované pláně bude trvat O(MN+k4) a stejně prostoru bude zabírat výsledná datová struktura. Na dotazy pak budeme schopni odpovídat v konstantním čase.
 29-3-5 Dračí zámek (Zadání)
29-3-5 Dračí zámek (Zadání)
K zadání této úlohy jste všichni dostali nápovědu, totiž kuchařku o metodě Rozděl a panuj. Toho jste všichni správně využili, a třebaže došlá řešení využívala různé přístupy, vždy byly založeny na této metodě.
Takže jak se k úloze správně postavit? Připomeňme, že čtvercová mřížka má rozměry N × N, kde N je nějaká mocnina dvojky. Je snadné si všimnout, že pro N = 1 má úloha triviální řešení: máme jediné plné pole.
| N |
| 2 |
| N |
| 2 |
V každé z nich se teď nachází plné pole, tudíž i na ně se můžeme zavolat rekurzivně.
Celý algoritmus slouží zároveň i jako důkaz, že kteroukoliv mřížku velikosti N = 2k lze pokrýt dílky. Počáteční pozorování pro k = 0 je indukčním předpokladem, rozdělení na podmřížky indukčním krokem.
Pokud bychom chtěli algoritmus implementovat (což jsme od vás nepožadovali), je zajímavé se podívat na časovou složitost. Budeme následovat výše uvedený postup a vytvoříme funkci, která vždy položí nový dílek a navíc pro N > 1 zavolá rekurzivně čtyřikrát sama sebe. Samotný průběh funkce má konstantní časovou složitost (pouze vypočítáme polohu plného pole), takže zbývá vyřešit, kolikrát se zavolá.
| N2 |
| 4 |
| N2 |
| 2 |
| N2 |
| 4 |

 29-3-6 Obrazec pro draka (Zadání)
29-3-6 Obrazec pro draka (Zadání)
Pro jednodušší řešení úlohy je dobré převést si mnohoúhelník na něco, s čím se pracuje lépe. Vytvoříme si graf, jehož vrcholy představují trojúhelníky a hrany reprezentují tyče. Vrcholy sousedních trojúhelníků jsou tedy spojené hranou. Ještě se nám bude hodit, když i strany mnohoúhelníku budou hrany a za každou stranou budeme mít také vrchol. Můžeme si všimnout, že tento graf je stromem.
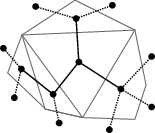
Nyní si můžeme vybrat jeden z vrcholů mimo mnohoúhelník a prohlásit ho za kořen našeho, nyní binárního, stromu. Teď by nás zajímalo, co udělá s naším stromem jedno překlopení tyče. Ukážeme si, že odpovídá operaci stromové rotace.
Rotace je „otočení“ hrany mezi dvěma vrcholy, kde zachováme pořadí vrcholů a podstromy převěsíme, viz obrázek.
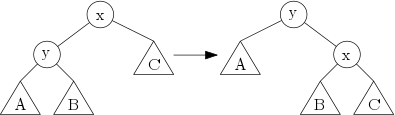
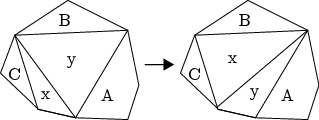
Počáteční i cílový obrazec převedeme na binární strom, kde za kořen zvolíme ten stejný vrchol (neboli vrchol za stejnou stranou mnohoúhelníku). Teď hledáme, jak převést pomocí rotací jeden na druhý. Ještě je dobré si očíslovat listy – tedy vrcholy za hranami mnohoúhelníku. Aby dva stromy reprezentovaly stejnou triangulaci, tak musí sedět i očíslování listů.
Stromové rotace mají jednu důležitou vlastnost, totiž zachovávají pořadí listů. Nestane se nám tak, že by se pořadí listů nějakým způsobem pomíchalo (což by znamenalo, že by se nám i mnohoúhelník musel nějak překlápět). Zachování této vlastnosti je důležité, protože bychom jinak mohli sice vymyslet způsob, jak přejít od jednoho stromu k druhému, ale neseděly by nám listy, tedy by vlastně vůbec nemuselo jít o tu samou triangulaci.
Nyní už jsme velmi blízko cíle. Připomínáme, že hledáme libovolnou posloupnost rotací, nemusí být nutně nejkratší. Pokud budeme opakovat dostatečně dlouho rotace do jednoho směru, třeba doleva, získáme lineární strom.
Stačí začít u kořene a opakovat rotace, dokud není vpravo jenom list. Poté půjdeme k jeho pravému synovi a budeme to opakovat. V každé rotaci jeden vrchol zařadíme do lineárního stromu a tedy nám to bude trvat O(n) kroků.
To samé můžeme provést s cílovým stromem. Využijeme toho, že k rotaci vpravo je rotace vlevo inverzní operací. Abychom získali hledanou posloupnost překlopení, můžeme provést rotace stromu počátečního obrazce na lineární strom a pak pozpátku ty, co jsme provedli s cílovým stromem.
Strom sestrojíme v lineárním čase, obě převedení na lineární strom zvládneme O(n) rotacemi, a protože každá trvá jen konstantní čas, tak celkový čas bude O(n). Počet rotací bude také O(n).
Najít nejkratší posloupnost rotací, která převádí jeden binární strom na druhý, v polynomiálním čase zatím bohužel neumíme. Jestli to vůbec jde, je stále otevřený problém. Umožnilo by nám to efektivně spočítat rotační vzdálenost dvou stromů, totiž kolik nejméně rotací je potřeba pro převedení jednoho stromu na jiný. To je hezká metrika – způsob, jak měřit „vzdálenost“ (rozdílnost) dvou stromů.
 29-3-7 Stromoví předci (Zadání)
29-3-7 Stromoví předci (Zadání)
Úkol 1: Chytřejší značkování
Ke kořeni chceme stoupat z obou vrcholů současně. Jelikož nám asi nedali paralelní počítač, budeme to co nejvěrněji simulovat. Vždycky jeden krok na cestě z prvního vrcholu, pak jeden z druhého, a tak dále. Vrcholy na obou cestách značkujeme a jakmile první vrchol dostane obě značky, je to hledaný společný předchůdce (LCA).
Jak dlouho to trvá? Označme d1 a d2 vzdálenosti k LCA. Tento LCA dostane první značku po d1 krocích, druhou po d2. Algoritmus se tedy zastaví po O(max(d1,d2)) krocích, což je totéž jako požadovaných O(d1+d2).
Úkol 2: Minimum svislé cesty
Chceme počítat minimum ohodnocení hran na „svislé“ cestě mezi vrcholem x a jeho předkem p. Předpočítáme si hloubky vrcholů d(v), takže dotaz umíme přeložit na minimum na cestě mezi x a Pra(x,d(x)-d(p)).
V zadání jsme ukázali, jak si předpočítat skočky, tedy hrany z v do Pra(v,2i), a pak počítat Pra(w,k) složením O(log n) skoček. Nyní si pro každou skočku předpočítáme ještě minimum z ohodnocení přeskakovaných hran. To pro každou zvládneme v konstantním čase složením dvou už spočítaných minim. A při skládání Pra(v,2k) ze skoček rovnou složíme i příslušná minima.
Předvýpočet trvá O(n log n), pak odpovídáme v O(log n).
Úkol 3: Součet svislé cesty
Součet je mnohem jednodušší. Spočítáme si analogii prefixových součtů, tedy součty S(v) všech hran z kořene do v. Součet na cestě mezi x a jeho předkem p pak je prostě S(x)-S(p). Předvýpočet trvá O(n), na dotazy odpovídáme v O(1).
Úkol 4: Minimum obecné cesty
Minimum nebo součet na obecné cestě mezi x a y spočteme tak, že nejdříve nalezneme ℓ= lca(x,y). Pokud je x=ℓ nebo y=ℓ, cesta je svislá a jsme hotovi. V opačném případě cestu rozložíme na dvě svislé cesty: z x do ℓ a z ℓ do y, pro které už umíme odpovědět.
Úkol 5: Součet pomocí ET-posloupnosti
Dostaneme ET-posloupnost, do níž jsme při průchodu hranou směrem dolů napsali její ohodnocení, a při návratu nahoru minus ohodnocení. Chceme počítat součty na svislých cestách, opět označíme x nižší vrchol cesty a p ten vyšší.
Nejprve dokážeme, že součet všech čísel mezi dvěma výskyty téhož vrcholu v v ET-posloupnosti je nulový. Určitě to stačí dokázat pro „sousední“ výskyty, tedy takové, mezi nimiž jsme v nenavštívili. Nechme DFS běžet tak dlouho, než dospěje do prvního z našich dvou výskytů vrcholu v. Pak bude pokračovat do některého ze synů vrcholu v, načež proleze celý podstrom pod tímto synem, a nakonec se vrátí zpět do v, což bude druhý z výskytů. Kdykoliv při tomto průchodu prošel po nějaké hraně dolů, vrátil se po ní pak nahoru, takže k celkovému součtu tato hrana přispěje nulou.
Nyní dokážeme, že součet všech čísel mezi jakýmkoli výskytem vrcholu p a jakýmkoli výskytem vrcholu x je roven součtu cesty mezi x a p. Vzhledem k předchozímu odstavci si můžeme vybrat konkrétní výskyty: pro p si vybereme ten, z nějž odejdeme hranou vedoucí směrem k x; pro x zvolíme první výskyt.
Uvažujme, co DFS provede mezi těmito dvěma výskyty. Určitě prošlo po cestě z p do x. Všechny podstromy odpojující se od této cesty doleva, kompletně prošlo, takže celkem přispěly nulou. Podstromy odpojující se vpravo vůbec nenavštívilo. Nenulou tedy přispěly pouze hrany na cestě.
K odpovídání na daný typ dotazů tedy stačí předpočítat prefixové součty pro ohodnocenou ET-posloupnost, a pamatovat si pro každý vrchol jeho libovolný výskyt. To zvládneme v lineárním čase, na dotazy pak odpovídáme odečtením dvou prefixových součtů, tedy v konstantním čase.
Úkol 6: Syn v zadaném směru
Dostaneme vrchol x a jeho předchůdce p. Chceme najít toho ze synů vrcholu p, který leží na cestě z p do x. Použijeme podobný trik jako pro výpočet LCA. ET-posloupnost ohodnotíme hloubkami a budeme hledat vrchol s minimální hloubkou ležící mezi libovolným výskytem vrcholu x a posledním výskytem vrcholu p.
Z toho přímo nic nezjistíme: minimum se evidentně nabývá pro vrchol p. Ale pokud v zadaném intervalu nalezneme nejlevější minimum, je to ten z výskytů vrcholu p, do nějž jsme se z x vrátili. Těsně před ním v posloupnosti leží hledaný syn.
Stačí nám tedy vylepšit strukturu pro intervalová minima, aby vždy našla nejlevější výskyt minima v intervalu. To se dá zařídit třeba tak, že do ET-posloupnosti pro i-tý výskyt vrcholu v místo hloubky d(v) zapíšeme uspořádanou dvojici (d(v),i) a dvojice budeme porovnávat lexikograficky. Nebo můžeme dvojici zakódovat do přirozeného čísla d(v)·n + i.
Takto upravená struktura bude stejně rychlá jako ta původní, takže s předvýpočtem v O(n log n) dokážeme odpovídat v konstantním čase.