Pátá série dvacátého devátého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu pošleme každému, kdo ze série získá alespoň 29 bodů.
Zadání úloh
Naposledy se vrátíme k našim udatným hrdinům, se kterými jsme se potkali už
v první a třetí sérii. Opustili jsme je potom, co zažehnali problém s drakem,
a chystali se vydat dále na sever, aby zjistili, kdo za tím vším stojí.
* * *
Sirovi Warinovi, členovi Alvarezova řádu, právě končila hlídka. Už dva dny
pozorovali hrad, kam je dovedly zápisky v deníku z jeskyně s drakem, a došli
k tomu, že tu musí být nějaký velmi silný temný mág.
„Vydáme se dovnitř,“ řekl Warin ostatním, „ale nejdříve dáme vědět králi.
Gorfe, můžeš připravit poštovního holuba?“ obrátil se s dotazem k jejich
lučištníkovi a nadanému zloději. „A my ostatní,“ podíval se na kouzelnici
Rheu a na mladého rytíře Liana, „se zatím připravíme na proniknutí těmi
tajnými chodbami.“
Gorf přikývl a šel chystat holuba. Poslat zprávu holubí poštou ale nebylo jen
tak, bylo potřeba naplánovat, kudy má putovat.
 29-5-1 Holubí pošta (10 bodů)
29-5-1 Holubí pošta (10 bodů)
Skupina hrdinů potřebuje co nejrychleji poslat zprávu holubí poštou do hlavního
královského města. Je to ale velká vzdálenost, takže je potřeba zprávu poslat
přes několik mezilehlých měst, kde se vždy vystřídají holubi.
Hrdinové mají mapu království jako graf, ve kterém vrcholy jsou města a hrany
značí, mezi jakými městy je možné zprávu poslat (hrany jsou orientované). Každá
hrana je ohodnocená časem, jak dlouho trvá holubovi přelet.
Ale aby to nebylo tak jednoduché, tak z každého města neodesílají zprávy
nonstop, ale odesílají je jen v pracovní dobu této poštovní stanice. Pokud
přiletí holub v průběhu pracovní doby, je zpráva hned předána dál, pokud ale
přiletí mimo pracovní dobu, je zpráva odeslána dál až s opětovným zahájením
pracovní doby.
Pro každé město budete mít zadané pravidelné intervaly pracovní doby a vaším
úkolem je v této síti holubí pošty naplánovat časově nejkratší cestu mezi
zadaným startem a královským hlavním městem.
Formát vstupu: Na prvním řádku dostanete počet měst N, počet hran M,
index počátečního města S (indexujeme od nuly) a index královského města K.
Poté bude na dalších N řádcích následovat popis měst a jejich pracovní doby
a na dalších M řádcích pak popis hran. Všechny časové údaje jsou v celých
hodinách a pokud holub přiletí na konci pracovní doby, tak je také zpráva
odeslána ještě hned (tedy pracovní dobu bereme včetně koncových hodin). První
holub vylétá vždy v čase 0.
Na i-tém řádku popisujícím města je zadaný popis města i jako trojice čísel
intervali, delkai, offseti udávající
interval, po jakém se opakující pracovní doby, délku pracovní doby a offset,
s jakým je začátek první pracovní doby posunutý. Tedy například popis 5 2 1
znamená, že pracovní doba je mezi hodinami 1 až 3 (offset 1 a délka 2) a opakuje
se po 5 hodinách (tedy další je mezi hodinami 6 až 8, další pak 11 až 13 atd.).
Vždy bude platit, že délka i offset budou maximálně tak velké, jako interval.
Popis hran je jednoduchý, na j-tém řádku popisů hran je trojice čísel a, b, h
udávající, že j-tý holub letí z města a do města b a trvá mu to h hodin.
Formát výstupu: Na první řádek výstupu vypište délku cesty v hodinách,
na druhém řádku pak vypište mezerami oddělenou posloupnost měst (včetně prvního
a posledního), kterými tato nejkratší cesta vede.
Ukázkový vstup:
4 4 0 2
2 2 0
4 2 0
8 8 8
20 3 1
0 1 11
1 2 10
0 3 5
3 2 5
Ukázkový výstup:
22
0 1 2
I když doby čistého letu přes vrchol 3 jsou kratší, tak zde hůře vychází
pracovní doba v mezilehlém městě (odeslání z města 3 by proběhlo až v čase 21,
kdežto z města 1 odlétne holub již v čase 12).
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Řešení
Holub se zprávou na noze odlétl do podmračeného nebe a čtyři dobrodruzi se
vydali lesem ke vstupu do jeskyní pod hradem. Všimli si, že skrz hradní bránu
sice chodí mnoho skřetů, ale jeskynní vstup používají i různé tajemné postavy
v pláštích.
Jeskyně byla osvětlená pochodněmi a nikdo ji nehlídal, ale kousek za vstupem
byla velká brána. A ten, kdo ji zkonstruoval, se pravděpodobně vyžíval
v roztodivných zámcích, podobně jako u truhlice v dračí jeskyni. Tady to
vypadalo trochu, jako kdyby zámek zkonstruovali trpaslíci – byly to různě
natažené dráty, po kterých přeskakovaly modré jiskry magie.
Rhea vytáhla ukořistěný deník a začetla se do něj. Minuty ubíhaly a oba rytíři
pozorně sledovali okolí, jestli se odněkud nevynoří nějaký skřet. I Gorf začínal
být nejistý a žmoulal v ruce připravený šíp. Náhle Rhea nalezla správnou
pasáž a odcitovala „Nejtenčí na každém kruhu, ten pozbyt má být svých druhů.“
Když se pozorně podívali na dveře, skutečně spatřili, že každý drát je jinak
tlustý a každý se dá odpojit.
 29-5-2 Odcyklení zámku (11 bodů)
29-5-2 Odcyklení zámku (11 bodů)
Hrdinové se opět dostali k podivnému zámku. Tento zámek vypadá tak, že se skládá
z mnoha vrcholů propojených dráty, po kterých přeskakují magické výboje.
Každý drát má nějakou svoji tloušťku.
Podle pokynů z deníku je potřeba odpojit nějaké dráty tak, aby
zanikly všechny cykly.
Není to ale tak jednoduché, v každém cyklu lze vždy odpojit jen ten
nejtenčí drát (jinak by se obíhající mana vyzkratovala a to nikdo nechce).
Najděte tedy nějakou posloupnost drátů, které budete odpojovat a které ve chvíli
odpojení musí být tím nejtenčím drátem (nebo jedním z více nejtenčích drátů) na
alespoň jednom cyklu.
Jak už bylo řečeno výše, může existovat více drátů se stejnou tloušťkou
a řešení tedy nemusí být jednoznačné. Nemusí být dokonce jednoznačné ani v počtu
drátů, které je potřeba odpojit. Stačí najít jedno libovolné řešení.
Například pro následující graf:
je správným řešením odebrat hrany např. v pořadí
AC (nejkratší na
ACDEA),
BC,
BD. Jiným správným pořadím může být
BC,
ED,
BD.
Řešení
Rhea jednou omylem sáhla na jiný než nejtenčí drát a dostala ránu, po které ji
na pár minut ochrnula pravá ruka. Pak si ale již dávala pozor a brána se před
nimi po odpojení posledního z drátů pomalu otevřela. Opatrně prošli dovnitř
a dostali se po pár metrech na rozcestí chodeb. Brána se za nimi zase neslyšně
uzavřela.
Z jedné strany se ozval hluk, a tak se hrdinové ukryli na chvíli do malé jeskyně
na straně. Za pár sekund okolo překlusala malá skupinka skřetů, takže se
hrdinové mohli vydat dál.
Pod hradem bylo celé bludiště chodeb. Kryti maskovacím kouzlem vyslechli
rozhovor skřetů, kteří se bavili o nejlepší technice sekání hlav, později zase
schováni za hromadou sudů sledovali skupinku mágů oděných v černém, jak
provádějí nějaký okultní rituál. Bylo tu mnoho skřetů, o něco menší počet
goblinů, zahlédli i skupinu trollů a sem tam se mihlo pár temných mágů. Některé
části jeskyní kypěly životem, takže se k nim radši moc nepřibližovali, v jiných
částech se zase táhly dlouhé temné chodby bez života. V jedné takové se po pár
hodinách posadili nad rychlým jídlem.
„Nějaké nápady, kde by mohl být jejich vůdce?“ řekl potichu Warin, když
ukusoval chleba. „Ve skřetí části ne, té se ti temní mágové vyhýbají,“
přemýšlel Lian, „ale jinak nemám ani potuchy, je to tu moc rozlehlé. A navíc
jsme jen čtyři, těžko se budeme někam probíjet!“
„Hmm… a co někoho unést? Promluví, já už ho k tomu nějak přinutím!“
potěžkal Gorf svůj lovecký nůž. „Zadrž, mám lepší řešení,“ zastavila ho Rhea,
„umím namíchat sérum pravdy.“
Rychle dojedli a vydali se zpátky k obydleným částem jeskyní. Vyhlédli si
jednoho osamoceného mága a opatrně ho sledovali. Když zašel do boční chodby, byl
jejich. Gorf k němu rychle přiskočil a přitiskl mu nůž pod krk: „Pohni prstem
a je po tobě!“ sykl. Dotáhli ho dál od obydlených částí a Rhea začala míchat své
lahvičky.
 29-5-3 Sérum pravdy (8 bodů)
29-5-3 Sérum pravdy (8 bodů)
Kouzelnice Rhea by potřebovala namíchat sérum pravdy, aby od zajatého temného
mága zjistila důležité informace.
Jednou z ingrediencí je i rosa sbíraná o půlnoci. Ale musí jí být správné
množství a co je ještě důležitější, tak se nedá bezmyšlenkovitě míchat rosa
z náhodných nocí. Pokud už se nějaká musí míchat, tak jedině z několika po sobě
navazujících nocí.
Rhea má teď před sebou postavenou řadu lahviček s kapkami rosy nasbíranými
každou noc. Vzhledem k váze zajatého mága ví, že bude potřebovat množství co
nejbližší K kapkám rosy.
Pomozte ji vybrat úsek lahviček, které dají dohromady součet kapek nejvíce se
blížící zadanému K (obsah každé lahvičky je potřeba použít celý). Z některých
nocí také může být v lahvičce jen rosná mlha (lahvičky s obsahem 0 kapek), ale
ty je potřeba uvážit taky.
Příklad: Například pro K=12 a lahvičky s počty kapek 15,3,6,0,4,0,0,7,8
existuje více optimálních řešení. Jedno z nich je vzít čtyři lahvičky
3,6,0,4 se součtem 13, jiným řešením je třeba vzít lahvičky 4,0,0,7 se
součtem 11.
Řešení
Po podání séra pravdy temný mág promluvil a pověděl jim o málo používané cestě
k jejich vůdci. Sice je na této cestě čekají asi nějaké pasti, ale aspoň se
nebudou muset probíjet skrz hordy skřetů.
Uspaného temného mága nechali v temném koutě a vydali se cestou podle jeho rad.
Opatrně překročili několik natažených lan spouštějících samostříly ve stěnách
a postupovali dál. Po chvíli se zepředu začaly ozývat divné klapavé zvuky.
Přitisknuti ke stěnám se plížili opatrně dál, než se dostali na okraj větší
jeskyně.
Před nimi se jim naskytla podívaná na spoustu ozubených kol a rotujících kotoučů
s ostrými čepelemi, které jim zahrazovaly cestu na druhou stranu. Také tu stál
starý důlní vozík, který se dal roztlačit po kolejích skrz rotující čepele.
 29-5-4 Rotující čepele (11 bodů)
29-5-4 Rotující čepele (11 bodů)
Dobrodruzi se potřebují dostat na druhou stranu místnosti plné rotujících
čepelí. Čepele rotují příliš rychle na to, aby mezi nimi šlo proběhnout, ale
po podlaze místnosti vedou koleje a mohou se pokusit projet skrz důlním vozíkem.
Důlní vozík lze rozjet nějakou rychlostí (z rozsahu minimální a maximální
rychlosti vozíku) a touto rychlostí pak projede celou místností (nemůže už
brzdit ani zrychlovat).
Každá z rotujících čepelí je postavená kolmo na směr jízdy, má nějakou
vzdálenost od začátku jeskyně a víme pro ni délky intervalů, kdy je jí bezpečné
projet a kdy ne (ty se periodicky opakují, protože čepel rotuje stále stejnou
rychlostí). V čase 0 jsou všechny čepele na začátku svého bezpečného intervalu.
Vymyslete postup, který pro zadané čepele a zadanou minimální a maximální
rychlost vozíku najde jednu rychlost, kterou vozík zvládne projet skrz všechny čepele
až na druhou stranu jeskyně (vozík vždy vyrazí z bodu 0 v čase 0), nebo
rozhodněte, že takovou rychlost nalézt nejde.
Například mějme vozík s rozsahem rychlostí 1,5 až 4 m/s a dvě čepele.
První má bezpečný i nebezpečný interval dlouhý 2 s a je vzdálena 12 m.
Druhá má bezpečné okno 5 s, nebezpečné 3 s a je vzdálena 36 m.
V tomto případě je správným řešením např. rychlost 3 m/s. Při ní
projedeme první čepelí v čase 4 s (těsně na začátku druhého bezpečného
okna) a druhou v čase 12 s (uvnitř bezpečného intervalu od 8 s do 13 s).
Jiným správným řešením je rychlost 2 m/s.
Řešení
Na druhé straně si všichni oddychli, trefit správnou chvíli na průjezd skrz
čepele nebylo snadné.
Z konce jeskyně stoupaly nahoru dlouhé točité schody. Vydali se po nich opatrně
nahoru. Po nějaké chvíli se stěny jeskyně změnily v stěny z kamenných kvádrů,
to když vystoupali až do samotného hradu. Po chvíli je jejich kroky zavedly do
malé místnosti, na jejímž opačném konci byly kamenné dveře a vedle nich socha
znázorňující sfingu.
„Vítej u dveří… Beliarových… kolik… podob mám?“ přečetl Lian otázku
napsanou starými runami nad hlavou sfingy. „Co to znamená?“
„V deníku o tom nic není, ale je tady jedna dlouhá zašifrovaná pasáž,“
odpověděla Rhea.
„A nepomůže nám vědět, že je v ní zapsaná tahle otázka?“ napadlo Gorfa. Rhea
se zamyslela a zadívala se na zašifrovaný text…
 29-5-5 Zašifrovaný text (12 bodů)
29-5-5 Zašifrovaný text (12 bodů)
V deníku se nachází dlouhá pasáž zašifrovaná pomocí Vigenerovy šifry. Ta funguje
tak, že vezme dlouhou zprávu a nějaký (typicky kratší) klíč a šifruje jednotlivé
znaky zprávy do posunutých abeced. Posun abecedy pro konkrétní písmeno vždy určí
odpovídající znak klíče – pokud šifrujeme k-té písmeno zprávy, šifrujeme do
abecedy posunuté tak, aby začínala na k-tý znak klíče (tedy pokud je k-tý
znak zprávy a, je posunutá abeceda stejná jako normální). Pokud je
zpráva delší než klíč, tak klíč opakujeme dokola.
Ukázka zprávy zašifrované pomocí klíče beliar:
vitejudveribeliarovych
+ beliarbeliarbeliarbeli
= wmemjlezpzisfptirfwcnp
Prolomit Vigenerovu šifru bez nějaké další informace je docela těžké. Naštěstí
naši hrdinové znají větu, která by se ve zprávě měla objevit, a navíc ví, že tato
věta je řádově delší než klíč.
Vymyslete algoritmus, který pro danou zašifrovanou zprávu a pro větu, která se
v původním textu vyskytuje, nalezne klíč, kterým lze zprávu dešifrovat. Tím
myslíme najít nějaký klíč, jehož odečtením od zašifrované zprávy dostaneme
zprávu, ve které se někde vyskytuje zadaná věta.
Pokud je délka klíče K, máte slíbeno, že délka známé věty bude
alespoň K2. Pro některé texty a věty může existovat více řešení, můžete
vybrat libovolné z nich.
Řešení
Skutečně, po chvíli snažení se jim díky odhadnuté větě povedlo pasáž dešifrovat
a nalézt v ní odpověď. Po jejím vyřčení se dveře se skřípotem otevřely. Skrz
dveře se dostali do velké místnosti obehnané gobelíny.
Než se však stihli rozkoukat, řítila se k nim vysoká postava v černém plášti,
okolo které vyzařovala rudá aura. „Co tu děláte!?!“ zahřímal hlas, který
vůbec nezněl jako z tohoto světa. To musel být vůdce skřetích hord, temný mág
Beliar!
Než stihli zareagovat, vrhl k nim Beliar blesk. Gorf na poslední chvíli uskočil
a blesk rozštípl kamennou zeď za jeho zády. Odletující úlomky kamene na chvíli
vyvedly z rovnováhy i samotného Beliara a daly tak naší skupince čas se
rozptýlit po místnosti.
Gorf vyslal několik šípů, ale ty se odrazily o silový štít, který Beliar okolo
sebe vytvořil. Z boku místnosti se začali hrnout skřeti, a tak Warin s Lianem
vyběhli tím směrem mávaje meči a působíce zmatek a zděšení.
Kouzla létala vzduchem. Ani Rhea, ani Beliar neměli nad tím druhým navrch, ale
Rhee rychle docházely síly. Držela svůj ochranný štít a pokoušela se sestavit
z dostupných sil co nejsilnější kouzlo.
 29-5-6 Nejsilnější kouzlo (10 bodů)
29-5-6 Nejsilnější kouzlo (10 bodů)
Kouzelnice Rhea bojuje s mágem Beliarem a potřebovala by seslat zvlášť mocné
kouzlo. Mocná kouzla se čtou ze svitků a v tomto typu kouzlení většinou platí,
že čím je kouzlo delší, tím je také silnější. A ta nejsilnější kouzla mají často
i nějaké speciální vlastnosti, třeba že jsou palindromy (tedy že se stejně čtou
ze začátku i z konce).
Vymyslete algoritmus, který v zadaném textu (posloupnosti písmen) najde nejdelší
palindrom (v případě více nejdelších palindromů libovolný z nich).
Příklad: V textu aasqaanaaqqaaert je nejdelším palindromem
qaanaaq o délce 7 znaků.
Řešení
Ani Beliar ale nezahálel. Těsně před tím, než svoje kouzlo měla připravené Rhea,
vyslal svoje kouzlo k ní. Warin vše sledoval jako ve zpomaleném filmu. Jak
Beliar zvedá ruku s holí. Jak se on sám odráží z paty a mečem rozpolcuje jednoho
skřeta vedví. Jak se na Beliarových prstech tvoří koule magie. Cítil vlastní štít
a to, jak běží a skáče. A pak si magická koule našla jeho štít a rozprskla se
o něj…
* * *
Probudil se a okolo bylo nesnesitelné světlo. Zamrkal. Pak ještě jednou a okolo
se začaly vynořovat obrysy místnosti. Místnosti, kde sváděli boj. Ale teď tu
bylo ticho. Tedy skoro.
„No tys nám dal. Myslím, že budeš potřebovat nový štít,“ smála se radostí
Rhea, nad kterou se skláněl ještě Gorf. Warin se podíval dolů na své spálené
brnění a na zbytky pokrouceného kovu, které bývaly štítem z mithrilu. Ruka ho
pekelně bolela, ale hýbat s ní mohl. „Co se…?“
„Vyhráli jsme. To, jak jsi vlétl do toho kouzla, bylo hrozně hrdinské, ale
hrozně nezodpovědné,“ pokárala ho Rhea, „ale dal jsi mi čas dokončit kouzlo
a tím porazit Beliara. Po zhroucení jeho sil se rozpadl na prach a všechny
skřety jako by popadl amok. Začali se zabíjet navzájem. Lian ještě čistí tohle
patro, ale myslím si, že jsme vyhráli.“
S Gorfem pomohli Warinovi na nohy a vydali se k balkonu. Lian se k nim vzápětí
připojil a společně vyšli ven. Dole se od hradních bran ještě vzdalovaly malé
skupinky skřetů. Potom, co zmizela vůle ovládající je, utíkali zpátky domů.
Severní země byly (aspoň nyní) zachráněny, a to díky této udatné skupince hrdinů.
Jejich cestu s vámi sledoval
Jirka Setnička
 29-5-7 Stromy v pohybu (15 bodů)
29-5-7 Stromy v pohybu (15 bodů)
Vítejte u posledního dílu stromového seriálu. Propukne v něm malá
revoluce: chystáme se porušit předpoklad ze všech předchozích dílů,
že celý strom známe na začátku výpočtu a pak už jeho tvar zůstává
navěky stejný. Postupně vybudujeme datovou strukturu,
která bude umět udržovat obecný les a stromy libovolně spojovat
a rozdělovat. Bude inspirována Link-Cut Trees od pánů
Sleatora a Tarjana.
Opakování vyhledávacích stromů
Podobně jako jsme dříve reprezentovali cesty pomocí intervalových
stromů, teď využijeme binární vyhledávací stromy (BVS).
Pokud jste se s nimi ještě nesetkali, nahlédněte do
kuchařky o vyhledávacích stromech.
Aby bylo jasné, kdy mluvíme o původních stromech a kdy o BVS,
pomocí nichž původní stromy reprezentujeme, budeme vrcholům BVS
říkat uzly.
Představme si binární vyhledávací strom, v němž je uložena jistá
množina čísel x1 < … < xn. Pokud tato čísla chceme vypsat
od nejmenšího do největšího, můžeme BVS projít rekurzivně v takzvaném
in-orderu: kdykoliv vstoupíme do nějakého uzlu u, nejprve rekurzivně
projdeme levý podstrom, pak vypíšeme číslo v uzlu u, a nakonec
rekurzivně projdeme pravý podstrom.
Nyní k BVS přidáme takzvané externí uzly: kdykoliv nějakému
uzlu stromu chybí syn, připojíme na místo tohoto syna nový uzel.
Strom jsme tedy opatřili ještě jednou vrstvou listů (když si představíte
reprezentaci stromu v programu, externí uzly budou na místech původních
NULL pointerů).
Zajímavou vlastností externích uzlů je, že odpovídají intervalům mezi
čísly v interních (původních) uzlech. Skutečně: při hledání libovolného
čísla z intervalu (xi,xi+1) dopadnou všechna porovnání v interních
uzlech stejně, takže skončíme v tomtéž externím uzlu.
Při in-orderovém průchodu stromem tedy začneme v nejlevějším externím
uzlu (ten odpovídá intervalu (-∞,x1)) a pak se pravidelně
střídají interní a externí uzly, až skončíme v nejpravějším externím
uzlu, tedy intervalu (xn,+∞).
Často se nám bude hodit najít nejmenší číslo uložené ve stromu. K němu
dojdeme tak, že se z kořene vydáme stále doleva. Když už to nejde dál, nacházíme
se v minimu: všechny prvky, přes něž jsme prošli, jsou větší, a stejně tak
vše, co leží od nich doprava. Časová složitost této operace je zjevně
lineární v hloubce stromu.
Úkol 1 [2b]
Vymyslete, jak v BVS nalézt následníka zadaného uzlu. Tím myslíme
uzel s nejmenším číslem, které je větší než to zadané. Dosáhněte složitosti
lineární s hloubkou stromu. Můžete předpokládat, že každý uzel si kromě ukazatelů
na své syny pamatuje i ukazatel na otce.
Splay stromy
Jelikož operace s BVS trvají lineárně s hloubkou stromu, musíme stromy
udržovat vyvážené – tehdy mají příjemnou logaritmickou hloubku. Existuje
mnoho způsobů vyvažování (třeba AVL stromy nebo červeno-černé stromy),
my tentokrát zvolíme jeden poněkud netradiční: takzvané splay stromy.
Jejich úplný popis naleznete v Medvědově knížce
v kapitole o amortizaci. Zde si vystačíme se základními principy.
Kdykoliv budeme pracovat s nějakým uzlem u, „vyrotujeme“ ho
do kořene stromu. Této operaci se říká splayování uzlu u,
a když se udělá správně (viz knížka), zabraňuje degeneraci stromu.
Občas se sice může stát, že nějaký uzel bude hodně hluboko, takže
přístup k němu bude pomalý. Ale až na něj sáhneme, splayování dlouhou
cestu rozkošatí a další operace budou zase rychlé.
Obecně platí, že jedno splayování může trvat až O(n), ale posloupnost
jakýchkoliv k po sobě jdoucích splayování trvá O(n log n + k log n).
Dlouhodobě se tedy splayování chová, jako by mělo logaritmickou složitost
(říkáme, že je amortizovaně logaritmické).
Nyní si rozmyslíme, jak se ve splay stromu hledá minimum. Půjdeme stále
doleva dolů, jako v obecném BVS, a až dorazíme do minima, vysplayujeme
ho do kořene. Hledání minima trvalo lineárně s hloubkou minima a stejně
tak splayování. Ovšem splayování je amortizovaně logaritmické, takže
pro hledání minima to musí platit také. (Můžeme si také představit, že jsme průchod
jednotlivými hranami shora dolů naúčtovali jejich průchodu zdola nahoru během
splayování, čímž jsme splayování zpomalili konstanta-krát.)
Úkol 2 [1b]
Zkombinujte hledání následníka z prvního úkolu se splayováním tak,
aby mělo amortizovaně logaritmickou složitost.
Teď zkusíme splay stromy rozdělovat a spojovat.
Mějme nějaký uzel u a chceme strom rozdělit na dva stromy: v jednom
budou hodnoty menší než v uzlu u, v druhém ty větší. Samotný uzel u
zmizí. Zatímco v AVL stromech by to byla docela obtížné, ve splay stromu
je to triviální: vysplayujeme u do kořene a všimneme si, že všechny menší
hodnoty jsou momentálně v levém podstromu pod u a všechny větší v tom pravém.
Stačí tedy u smazat.
Spojování je ještě jednodušší: dostaneme nějakou hodnotu x a dva stromy –
v prvním budou všechny hodnoty menší než x, v druhém větší. Vytvoříme nový
uzel s hodnotou x, který se stane kořenem nového stromu. Jako levého syna
mu připojíme kořen prvního stromu, jako pravého syna kořen druhého.
Rozdělování a spojování můžeme například použít ke vkládání a mazání
hodnot. Tyto operace ale překvapivě nebudeme potřebovat.
Reprezentace cest
Splay stromy (SS) nyní využijeme k reprezentaci cest. Uvažujme nějakou orientovanou
cestu s vrcholy v0,… ,vk, mezi nimiž vedou hrany e1,… ,ek.
Vytvoříme BVS s k interními uzly, ve kterých sice nebudou uložena žádná
čísla (uvidíme, že to vůbec nevadí), ale jejich in-orderové pořadí bude
odpovídat hranám cesty. Pak přidáme externí uzly, které budou odpovídat
k+1 vrcholům cesty. Při in-orderovém průchodu tedy budeme navštěvovat
postupně
v0,e1,v1,e2,v2,… ,vk-1,ek,vk.
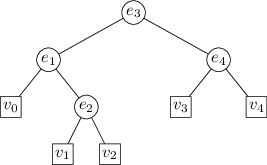
Cestu se čtyřmi hranami můžeme popsat třeba takto:
Postupně ukážeme, jak v této reprezentaci provádět některé základní
operace se souborem cest. Pro každou cestu si pořídíme jeden SS
a zapamatujeme si, kterému vrcholu a hraně cesty odpovídá který
uzel SS.
Ještě si rozmyslíme okrajové případy: cesta o jedné hraně je reprezentovaná
SS s kořenem (to je ta hrana), pod nímž visí dva externí uzly (krajní vrcholy
hrany). Jednovrcholová cesta bez hran odpovídá degenerovanému SS, jenž nemá
interní uzly a samotný kořen je externí.
Nyní operace:
- Path(v) – zjištění, do které cesty patří vrchol v: najdeme
odpovídající externí uzel SS a vystoupáme z něj až do kořene SS.
- First(p) – nalezení prvního vrcholu dané cesty: stačí najít
minimum příslušného SS, tedy jít pořád doleva. Symetricky Last(p) pro
poslední vrchol.
- Next(v) – nalezení následníka vrcholu (to je hrana, která vede
z v dále po cestě). Najdeme příslušný externí uzel x ve SS a půjdeme
do jeho následníka v in-orderu. Podobně Next(e) pro následníka hrany,
což je vrchol, a Prev(x) pro předchůdce vrcholu či hrany.
- Split(e) – rozdělení cesty na dvě odebráním hrany e. K tomu
použijeme už popsané rozdělení SS na menší a větší prvky.
- Split(v) – rozdělení cesty odebráním vrcholu v a hran, které
se ho dotýkají. Samotné v odpovídá externímu uzlu SS, takže ho nelze
jen tak smazat. Ale můžeme najít Prev(v) a Next(v), což jsou
hrany před a za v, a tyto hrany smazat. Tím se cesta rozpadne na tři
části: vše před v, vše za v a samotné v. Stačí tedy smazat třetí
část (ta má pouze externí kořen).
- Join(p1, p2) – spojení dvou cest hranou (za konec cesty p1
přidáme novou hranu a na ní napojíme začátek cesty p2). K tomu stačí
založit nový uzel SS odpovídající nové hraně cesty a jako syny tohoto uzlu
připojit kořeny obou SS.
- Reverse – otočení orientace cesty (poslední vrchol se stane
prvním a naopak). Do každého uzlu SS uložíme značku, zda je v celém
podstromu pod tímto uzlem prohozená levá a pravá strana. Kdekoliv
v podstromu může být samozřejmě další značka, která strany opět prohodí.
Značky budeme vyhodnocovat líně: kdykoliv při operacích se SS dojdeme
do vrcholu se značkou, prohodíme v něm ukazatele na syny a znegujeme
značky v synech. Na samotnou operaci Reverse pak stačí znegovat
značku v kořeni.
Úkol 3 [2b]
Navrhněte operaci pro spojení dvou cest za krajní vrcholy. Poslední
vrchol první cesty tedy splyne s prvním vrcholem druhé cesty.
Úkol 4 [3b]
Navrhněte, jak reprezentaci cest upravit, aby si u hran pamatovala
i celočíselné ohodnocení. Chceme umět operace „nastav hraně e ohodnocení x“
a „zjisti minimum z ohodnocení hran mezi vrcholy u a v“.
Dynamická dekompozice na cesty
Nyní vymyslíme, jak z cest skládat obecné stromy. Inspirujeme se
dekompozicí na lehké a těžké hrany z minulého dílu, ale tentokrát nebudou
druhy hran určeny velikostmi podstromů, nýbrž historií struktury, tedy
posloupností operací, které jsme zatím provedli.
Strom zakořeníme a všechny hrany zorientujeme směrem do kořene. Hrany
rozdělíme na tlusté a tenké. Která hrana bude tlustá, si můžeme
vybrat libovolně, ale musíme dodržet, že do každého vrcholu vede nejvýše
jedna tlustá hrana. Tlusté hrany tedy hrají podobnou roli jako těžké hrany
v HLD, tenké jako lehké.
Tlusté hrany proto tvoří cesty (orientované směrem ke kořeni) a každý vrchol
leží na právě jedné tlusté cestě (možná na triviální jednovrcholové). Z horního
vrcholu tlusté cesty může vést tenká hrana, kterou je cesta napojena k nadřazené
tlusté cestě.
Každou tlustou cestu budeme reprezentovat již popsaným způsobem pomocí splay
stromu. Poslední vrchol cesty w (v původním stromu leží nejvýše, ve splay stromu
je to nejpravější externí uzel) si bude pamatovat informace o tenké hraně do nadřazené
cesty: vrchol tparent(w), do nějž tenká hrana vede.
Vede-li tlustá cesta až do kořene, položíme tparent(w)=∅.
Nyní definujeme operaci Expose(v). Jejím úkolem je přestavět reprezentaci
stromu tak, aby z v do kořene vedla tlustá cesta, a navíc byl vrchol v jejím
začátkem. Budeme postupovat takto:
- p ←Path(v)
- Pokud First(p) ≠ v:
- e ←Prev(v)
- Rozdělíme p operací Split(e) na cesty p1 (dolní) a p2 (horní).
- tparent(Last(p1)) ←v
- p ←p2
- Dokud tparent(w) ≠ ∅, kde w=Last(p):
- x ←tparent(w)
- q ←Path(x)
- Pokud First(q) ≠ x:
- f ←Prev(x)
- Rozdělíme q operací Split(f) na cesty q1 (dolní) a q2 (horní).
- tparent(Last(q1)) ←x
- q ←q2
- p ←Join(p,q)
Kroky 2 až 6 ošetřují případ, kdy v není nejnižším na své tlusté cestě p.
Tehdy tuto cestu rozdělíme na dvě, které propojíme tenkou hranou. V krocích
7 až 15 cestu p postupně rozšiřujeme až do kořene: dokud ještě nevede do kořene,
je připojena tenkou hranou pod nějaký vrchol x ležící na jiné tlusté cestě q.
V krocích 10 až 14 zařizujeme, aby x byl nejnižším na q (jinak cestu q rozdělíme).
Jakmile x je nejnižší, můžeme cesty p a q propojit do jediné tlusté cesty
a pokračovat výš.
Na následujícím obrázku vidíme výsledek Expose(u):
Také se nám bude hodit operace Evert(v), která strom překoření do vrcholu v.
To se provede snadno: nejprve zavoláme Expose(v), čímž zařídíme, aby mezi v a starým kořenem
vedla jedna tlustá cesta, a tu pak operací Reverse obrátíme.
Nyní ukážeme, jak udržovat les zakořeněných stromů a provádět operace
s jejich strukturou. Každý strom bude reprezentovaný výše uvedeným způsobem
pomocí tlustých cest spojených tenkými hranami.
- Root(v) – vrátí kořen stromu, ve kterém se nachází vrchol v. Jednoduše
provede Expose(v) a pak se pomocí Last zeptá na poslední vrchol vzniklé
tlusté cesty.
- Parent(v) – vrátí otce vrcholu v (nebo ∅, pokud v je kořen).
Pokud následník Next(v) na příslušné tlusté cestě není ∅, vrátíme tohoto
následníka. Jinak z v vede tenká hrana, takže vrátíme tparent(v).
- Cut(v) – není-li v kořen, přeruší hranu mezi v a jeho otcem, čímž
strom rozdělí na dva. Může například provést Expose(v) a pak Split vzniklé
tlusté cesty ve vrcholu v.
- Link(u,v) – je-li u kořen jednoho stromu a v libovolný vrchol jiného stromu,
spojí oba stromy přidáním hrany z u do v. Na to stačí nastavit tparent(u) ←v.
Pokud chceme přidat hranu mezi dvěma vrcholy, které nejsou kořeny, stačí použít
Evert a jeden ze stromů překořenit.
Sleator s Tarjanem dokázali, že operace Expose má amortizovanou složitost
O(log n). Důkaz tohoto tvrzení je bohužel mimo možnosti našeho úvodního textu.
Je ale jasné, že z toho plyne, že i ostatní operace s dynamickými stromy mají
amortizovaně logaritmickou časovou složitost.
Úkol 5 [4b]
Upravte dynamickou dekompozici, aby si u každé hrany pamatovala i její celočíselné
ohodnocení. Chceme umět operace „nastav hraně e ohodnocení x“ a „zjisti minimum
z ohodnocení hran na cestě mezi vrcholy u a v“.
Úkol 6 [2b]
Navrhněte datovou strukturu pro inkrementální udržování minimální kostry.
Na počátku máme graf bez hran a postupně přidáváme ohodnocené hrany. Po každém
přidání chceme zjistit, jak se změnila minimální kostra.
Martin „Medvěd“ Mareš
Řešení
 29-5-1 Holubí pošta (10 bodů)
29-5-1 Holubí pošta (10 bodů)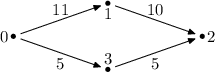
 29-5-2 Odcyklení zámku (11 bodů)
29-5-2 Odcyklení zámku (11 bodů)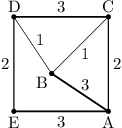




 29-5-7 Stromy v pohybu (15 bodů)
29-5-7 Stromy v pohybu (15 bodů)