Třetí série třicátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 30-3-1: Vlnění
- 30-3-2: Zmrazovač
- 30-3-3: Teleportér
- 30-3-4: Hmota a antihmota
- 30-3-5: Rozbití skupin
- 30-3-6: Střežení oblasti
- 30-3-7: Funkce očima assembleru
 30-3-1 Vlnění (Zadání)
30-3-1 Vlnění (Zadání)
Pokud nevíte, jak začít, tak je vždy dobré si vzít jednoduchý případ a ten si vyřešit „ručně“. Pomocí papíru a tužky šlo dokonce vyřešit jeden vstup, takže byste ani neodcházeli s prázdnou!
Při řešení tímto způsobem jste si pravděpodobně nakreslili dostatečný počet vln, zvýraznili obdélník a spočítali černé čtverečky. Není příliš velký problém toto uvažování převést do řeči nějakého programovacího jazyka.
Jednou z jednodušších variant, jak tento přístup naprogramovat, bylo postupovat po černých vlnách. Vždy projdeme celou vlnu a připočteme jedničku za každý čtvereček, který je v obdélníku. Jen musíme někdy skončit. Přestat můžeme v okamžiku, kdy pořadové číslo vlny přesáhlo minimální souřadnici (takové vlny se nacházejí již celé „za“ obdélníkem). Takto dostaneme řešení kvadratické vzhledem k minimální souřadnici.
Toto řešení lze snadno zrychlit. Při jeho programování si totiž můžete všimnout, že při procházení každé vlny nejprve vždy zahodíte všechny čtverečky, než se dostanete do obdélníka. A jakmile se dopočítáme na konec obdélníka, zase vyhodíme všechny zbylé čtverečky. Stačí tedy při procházení každé vlny skočit na první čtvereček v obdélníku a po vystoupení z obdélníka rovnou procházení vlny ukončit. Detaily jsou spíše technického rázu, a tak odkážeme na krátký vzorový program. Takto dostaneme řešení, které je lineární vzhledem k obsahu obdélníka.
Rychlejší řešení
Další zrychlení je velmi podobné. Všimneme si, že při procházení každé vlny vždy přičítáme jedničku, dokud se nedostaneme na konec. Tyto jedničky bychom měli být schopní přičíst najednou, tedy spočítat, kolik černých čtverečků z dané vlny je v obdélníku.
Abychom se do řešení nezamotali, započítáme zvlášť horní a pravou stranu vlny (nezapomeneme, že čtverečky na diagonále chceme započítat jen do jedné z těchto stran).
Budeme procházet nejprve horní strany. Nejprve si zajistíme, že budeme procházet jen ty vlny, jejichž horní strana je na úrovni obdélníku (tedy ani ne pod, ani nad). Toho lze snadno dosáhnout tak, že rovnou skočíme na vlnu s pořadovým číslem odpovídajícím y-ové souřadnici levého dolního rohu a přestaneme procházet vlny, až se dostaneme na y-ovou souřadnici pravého horního rohu.
Dále si u každé strany vyjádříme počet čtverečků uvnitř obdélníka. Pro to si nejprve vyjádříme počet černých čtverečků uvnitř a před obdélníkem (to je minimum z pořadového čísla vlny a x-ové souřadnice pravého horního rohu) a počet čtverečků před obdélníkem (to je minimum z pořadového čísla vlny a x-ové souřadnice levého dolního rohu). Pak stačí tato dvě čísla odečíst.
Abychom dostali konečný výsledek, posčítáme čtverečky z každé strany. Pro pravé strany je postup obdobný jako pro horní. Takto dostaneme řešení lineární ve větším rozměru obdélníka. Pro technické detaily opět doporučujeme pročíst vzorový kód.
Optimální řešení
Když si budeme procházet vlny dle předchozího řešení, uvědomíme si, že z každé vlny přičítáme podle určitého vzoru: Nejprve nic, dokud vlna nedosáhne obdélníku. Poté přičteme postupně p, p+4, …p+q, když je „roh“ vlny v obdélníku. Dále přičítáme nějaké r za jednu stranu a poté opět nic. To bychom mohli vyjádřit přímo, ale je to velmi náchylné na chybu (zvlášť když nějaká z těchto fází pro danou vlnu chybí). Proto na to půjdeme určitým trikem.
Nejprve si představíme, že náš obdélník je ve skutečnosti čtverec a navíc má levý dolní roh o souřadnicích (0,0). V takovém čtverci jsou vždy celé vlny, dokud vlna „nepřeteče“, a pak už do čtverce nezasahují vůbec. Z první černé vlny máme 3 černé čtverce, z druhé 7, z n-té 4n - 1. Tedy ze součtu všech vln dostaneme:
| n |
| i=1 |
V předchozím vzorci chápeme n jako počet černých vln, tedy dolní celou část ze souřadnice pravého horního rohu. Tento vzoreček je poměrně známý, ale lze k němu třeba dojít tak, že spolu sečtete první a poslední člen řady, druhý a předposlední atd.
Teď si představme, že nedostaneme čtverec, ale obdélník stále ukotvený rohem v (0,0). Budeme předpokládat, že šířka obdélníka je větší než jeho výška, ale řešení se v podstatě neliší. Souřadnice pravého horního rohu označíme (x,y). Obdélník si rozdělíme na čtverec (0,0) až (y,y) a obdélník (x+1,0) až (x,y). Černé čtverečky ve čtverci spočítáme podle předchozího odstavce.
Pro zbylý obdélník je řešení ještě jednodušší. Žádná vlna totiž v tomto obdélníku nemá roh, skládá se tedy ze sloupečků, které jsou celé bílé nebo černé. Sloupečků je x-y, polovina z nich černých (zda máme zaokrouhlovat dolů nebo nahoru, záleží na tom, jestli jsme začali černým sloupcem, tedy zda je y liché). Počet černých čtverečků pak už dostaneme jako násobek počtu černých sloupců jejich výškou (číslem y).
Nyní konečně případ, kdy nemáme levý dolní roh v (0,0). Zde použijeme trik, který někteří možná znáte z tzv. prefixových součtů. Máme totiž nástroj, jak rychle spočítat počet černých čtverečků v obdélníku ukotveném v počátku. Označme (x1, y1) souřadnice levého dolního rohu našeho obdélníka a (x2, y2) pravého horního. Začneme s obsahem obdélníka (0,0) až (x2,y2) (spočítaný podle předchozího odstavce). Jenže v tomto obdélníku jsou některé černé čtverečky navíc. Můžeme snadno odečíst černé čtverečky z obdélníku (0,0) až (x2,y1-1) a ještě odečteme čtverečky z obdélníku (0,0) až (x1-1,y). Teď jsme však odečetli čtverečky z obdélníka (0,0) až (x1-1,y1-1) dvakrát. Jenže počet černých čtverečků v tomto obdélníku umíme spočítat, není tedy nic jednoduššího, než je zpátky přičíst. Tím dostaneme požadovanou odpověď.
Počet černých čtverečků ve všech čtyřech obdélnících dokážeme spočítat v konstantním čase, stejně rychle tedy běží i celé řešení. Při psaní kódu je třeba si dát pozor na to, kde chceme přičíst a nebo odečíst jedničku a také kdy správně počítat zbytky po dělení prvočíslem ze zadání. Skutečně tedy doporučujeme přečíst si vzorový kód.
 30-3-2 Zmrazovač (Zadání)
30-3-2 Zmrazovač (Zadání)
Připomeňme si značení ze zadání: K je délka cesty, X je dosah zmrazovače. Jeden zmrazovač zasáhne celkem 2X + 1 políček (své vlastní, X nalevo a X napravo). Body na cestě číslujeme 0 až K-1. Dále si označíme N celkový počet nepřátel. Chceme umístit dva zmrazovače tak, aby dohromady zasáhly co nejvíce nepřátel.
Nejprve se zbavíme jednoho okrajového případu. Pokud K ≤ 4X + 2, můžeme postavit agenty tak, aby pokryli přesně celou cestu (konkrétně na pozice X a K-1-X). Zmrazí tedy všechny nepřátele a není co řešit.
Nadále budeme předpokládat K ≥ 4X + 3.
Též můžeme předpokládat, že v optimálním řešení se dosahy zmrazovačů nepřekrývají. Pokud bychom měli řešení, kde se překrývají, můžeme pravý z nich posouvat doprava (případně levý doleva, podle toho, na kterou stranu máme volné místo), dokud se překrývat nepřestanou. Žádné políčko tím neuvolníme z dosahu zmrazovače, takže se počet zasažených nepřátel nemůže snížit.
Zdánlivě lineární řešení
Nejprve si ukážeme řešení, které napadlo většinu řešitelů, ale není tak úplně optimální.
Pořídíme si pole P délky X, kde na pozici P[i] napíšeme počet nepřátel stojících na souřadnici i (typicky to bude 0 nebo 1, ale zadání nezakazuje víc nepřátel na jednom místě).
Nyní si pro každou pozici spočítáme, kolik nepřátel by zmrazil agent stojící na daném místě, a tato čísla uložíme do pole Z. To uděláme snadno. Představíme si, že po cestě posouváme okénko délky 2X + 1, které představuje dostřel zmrazovače. Na začátku jej postavíme středem na pozici 0 a spočítáme, kolik nepřátel okénko obsahuje.
Potom postupně posouváme okénko vždy o jednu pozici doprava. Po každém posunutí snadno v konstantním čase přepočítáme počet nepřátel uvnitř okénka: přičteme nepřátele na políčku, které se nově dostalo do okénka a odečteme nepřátele na políčku, které právě opustilo okénko. Ignorujeme části okénka, které přesahují mimo cestu, takže například prvních X posunutí nic neodečítáme. Po každém posunutí okénka si uložíme aktuální počet nepřátel pro daný středový bod i do Z[i]. Posunutí okénka trvá O(1), tedy celé pole naplníme v čase O(K).
Nyní by se nám líbilo postupně vyzkoušet všechna možná umístění levého zmrazovače a pro každé z nich vybrat nejlepší možné umístění pravého. Už víme, že by se dosahy neměly překrývat, tedy dáme-li levý zmrazovač na pozici i, pravý by měl být na pozici j ≥ i + 2X + 1. Ale zároveň chceme z povolených pozic vybrat takovou, kde zmrazí nejvíce nepřátel. Tedy vybereme takové j z rozsahu i + 2X + 1 až K-1, pro které je Z[j] maximální.
Tento výběr bychom zvládli v čase O(K), ale to je zbytečně pomalé. Namísto toho si nejprve spočítáme sufixová maxima pole Z. Ta fungují podobně jako prefixové součty, jen se počítají odzadu a s maximem místo součtu. Přesněji pořídíme si pole M a do M[i] uložíme pozici maxima na intervalu Z[i] až Z[K-1]. To zvládneme v čase O(K) jedním průchodem pole Z odzadu, při kterém si udržujeme průběžné maximum.
Nyní už pro danou pozici levého agenta i snadno v konstantním čase určíme pozici pravého – je to přesně M[i + 2X + 1]. Teď stačí vyzkoušet všechny možné pozice levého agenta, vybrat tu s nejlepším celkovým počtem zmražených (Z[i] + M[i + 2X + 1]) a v čase O(K) máme hotovo.
Hurá, lineární řešení!
Lineární?
Ehm…Kdykoli má úloha více parametrů, je třeba zamyslet se nad tím, lineární vůči čemu. Informatici obecně nemají rádi úlohy, jejichž složitost závisí na hodnotách čísel na vstupu a ne jen na jejich počtu.
Znamená to totiž, že existují maličké vstupy, na kterých program poběží v zásadě libovolně dlouho. Uvažte třeba vstup s pouhými dvěma nepřáteli, kteří stojí na pozicích 0 a 1018. Takovýto vstupní soubor bude mít pár bajtů, ale výstupu se nedočkáte (a ještě před tím vám dojde paměť, protože paměťová složitost je také O(K)).
Navíc: představte si, že vezmete nějaký existující vstup a souřadnice všech nepřátel (spolu s X a K) vynásobíte tisícem. Tím dostanete zcela ekvivalentní zadání (jen v jiném měřítku), ale váš program bude najednou tisíckrát pomalejší. To je obvykle špatné znamení.
Dá se na to dívat i formálně. Informatici, kteří se složitostí zabírají vážněji, ji obvykle měří v závislosti na celkové velikosti vstupu (v bitech). Zápis čísla K ve dvojkové soustavě je dlouhý log2 K bitů. Ale my na vstupu délky log2 K strávíme čas
Tedy toto řešení má vůči velikosti vstupu exponenciální časovou složitost. (A kdo byl na letošním jarním soustředění, ví, jak to může dopadnout, když člověk píše exponenciální řešení …)
Skutečně lineární řešení
Rádi bychom našli řešení pracující v čase O(N). Bude vycházet ze stejných principů jako předchozí řešení, ale už si nemůžeme dovolit používat pole indexované souřadnicemi nepřátel (to by se nám ani nemuselo vejít do paměti). Místo toho budeme pracovat nad setříděným seznamem S souřadnic nepřátel (zadání nám slibuje, že už jej setříděný dostaneme), který je dlouhý O(N).
Tady nám pomůže ještě jeden předpoklad: totiž, že v optimálním řešení stojí na levém okraji dosahu každého zmrazovače nepřítel. Pokud ne, můžeme zmrazovač posouvat doprava, dokud se tak nestane, což nesníží počet zasažených nepřátel. A stále přitom můžeme zachovat podmínku, že se dosahy nepřekrývají.
Odteď nebudeme popisovat umístění zmrazovače jeho pozicí, ale tím, kolikátý nepřítel stojí na levém okraji zasažené oblasti.
Analogicky jako předtím si budeme chtít spočítat pole Z[i] udávající, kolik nepřátel zasáhne zmrazovač, pokud na levém okraji jeho dosahu stojí i-tý nepřítel.
Použijeme opět posuvné okénko. Na začátku bude levým okrajem na prvním nepříteli a přičítáme do něj další nepřátele, dokud se do okénka vejdou (jejich vzdálenost od prvního je nejvýše 2X). Tím dostaneme hodnotu Z[0].
Nyní vždy okénko posuneme o jednoho nepřítele dál, toho odečteme a přičteme všechny, kteří se do okénka nově vejdou (průběžně si udržujeme pozici levého a pravého okraje okénka).
Jedno posunutí levého okraje může způsobit více posunutí pravého, ale protože se posouvá jen doprava, za celou dobu algoritmu se posune nejvýš N-krát. Celé pole Z tedy zvládneme naplnit v čase O(N).
Nyní bychom opět chtěli pro dané umístění levého zmrazovače vybrat nejlepší umístění pravého. Opět to bude takové j, aby Z[j] bylo maximální a dosahy se nepřekrývaly (tato podmínka je důležitá, protože kdyby se překrývaly, započítali bychom nepřátele v jejich průniku dvakrát).
Opět bychom si rádi předpočítali něco jako sufixová maxima. V tomto případě bychom chtěli, aby j = M[i] bylo číslo nepřítele takového, že jeho pozice S[j] je větší nebo rovna S[i] + 2X + 1 a zároveň počet zmražených Z[j] je maximální.
To uděláme zase tak, že projdeme seznam nepřátel zprava doleva. Ale tentokrát si pořídíme do tohoto seznamu dvě ukazovátka (levé i a pravé j). Na začátku dáme pravé ukazovátko na konec a levé posouváme od konce doleva tak dlouho, než je vzdálené alespoň 2X+1 (tedy S[j] - S[i] ≥ 2X+1). Průběžně si udržujeme pozici s maximálním Z[j], přes kterou přišlo pravé ukazovátko (jmax).
V každém kroku zapíšeme aktuální maximum na pozici levého ukazovátka (M[i] ← jmax). Poté posuneme levé ukazovátko o jednu pozici doleva. Následně posouváme pravé ukazovátko doleva, dokud můžeme (abychom neporušili podmínku na vzdálenost alespoň 2X+1).
Takto v čase O(N) naplníme pole M požadovanými maximy.
Nyní stačí vybrat nejlepší pozici levého agenta, tedy i, pro které je celkový počet zmražených Z[i] + M[i] maximální.
Hotovo, vystačíme si s časem i pamětí O(N).
Zde bychom se ještě měli přiznat k malé zradě. V zadání jsme schválně zdůraznili, že souřadnice jsou celočíselné, aby vás napadlo i horší řešení v O(K). Ale doufali jsme, že jej nakonec zavrhnete ve prospěch tohoto lepšího. Kdyby souřadnice nebyly celočíselné, je řešení v O(N) v zásadě jediné možné a člověk nemusí rozmýšlet, které vybrat.
Na druhou stranu jsme se vám snažili i trochu pomoci, konkrétně tím, že jsme slíbili předem setříděné souřadnice nepřátel. To proto, že kdyby se musely třídit, mohl by někdo nabýt mylného dojmu, že složitost O(K) je lepší než O(N log N). Není.
Nebuďte hladoví
Někteří řešitelé zkoušeli štěstí s hladovým algoritmem: nejprve umístím prvního agenta tak, aby zmrazil co nejvíc nepřátel. Tyto nepřátele smažu a pak umístím druhého tak, aby zmrazil co nejvíc ze zbylých. Toto řešení nefunguje.
Uvažte následující vstup s X=2:

Hladové řešení umístí prvního agenta na pozici 5, kde zmrazí 5 nepřátel. Ale druhý agent pak už může zmrazit maximálně 2 nepřátele, tedy celkem 7. Optimální řešení umístí zmrazovače na pozice 2 a 8, kde zmrazí každý 4 nepřátele, tedy celkem 8.
 30-3-3 Teleportér (Zadání)
30-3-3 Teleportér (Zadání)
Nejkratší cestě z nějaké základny X do hlavního sídla budeme říkat úniková cesta z X a její délce úniková vzdálenost z X (značíme U(X)). Dále si označme M délku nejdelší únikové cesty. Hledáme umístění teleportéru takové, aby M bylo co nejmenší.
Představme si cestu spojující základy jako vodorovnou, kde hlavní základna je úplně vlevo. Určitě se nikdy nevyplatí projít teleportérem ve směru zleva doprava, tím bychom se vzdálili od cíle a museli se vracet pěšky.
Dále si uvědomíme, že levý konec teleportéru můžeme vždy umístit do hlavní základny. Kdyby byl někde jinde, jeho přesunutím do hlavní základny se únikové cesty používající teleportér zkrátí a cesty nepoužívající teleportér se nezmění (případně také zkrátí, pokud se nově vyplatí teleportér použít). Určitě se ale odnikud úniková cesta neprodlouží.
Zbývá určit, kam umístit pravý konec teleportéru. To uděláme tak, že postupně vyzkoušíme všechna možná umístění, pro každé spočteme M a vybereme nejlepší řešení.
Představme si, že už jsme jej někam umístili (označme si toto místo T). Pak lze základny pomyslně rozdělit na tři úseky:
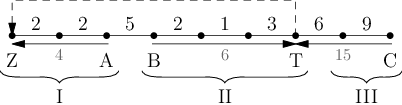
Úsek I tvoří základny, z nichž je nejkratší cesta do hlavního sídla pěšky, tedy takové, které jsou blíže k Z než k T. To jsou přesně základny ležící v levé polovině spojnice ZT (|ZX| < |ZT| / 2).
Můžeme si všimnout, že ze všech základen v úseku I má nejdelší únikovou cestu poslední základna, kterou si označíme A (U(A) = |ZA|). Ostatní základny z tohoto úseku můžeme tedy při výpočtu maxima ignorovat.
Úsek II naopak tvoří základny, ze kterých už se vyplatí jít doprava k teleportéru. Analogicky nejdelší úniková cesta v tomto úseku je z jeho první základny B (U(B) = |BT|).
Úsek III jsou základny napravo od T, ze kterých se vždy vyplatí jít přes teleport. Nejdelší úniková cesta v tomto úseku je z nejpravější základny C (U(C) = |TC|).
Když víme, že nejdelší úniková cesta je ze základny A, B nebo C, spočteme její délku snadno:
v našem případě max(4,6,15) = 15.
Abychom mohli M spočítat, potřebujeme:
- umět rychle určit vzdálenost dvou základen,
- vědět, kde je hranice mezi úseky I a II (základny A a B).
První úkol je jednoduchý: nad polem délek tunelů si spočítáme prefixové součty – tedy vlastně pro každou základnu spočítáme její tunelovou vzdálenost D(X) od hlavního sídla. Potom vzdálenost |XY| snadno spočítáme v konstantním čase jako D(Y) - D(X).
Základny A a B můžeme najít binárním vyhledáváním v poli prefixových součtů. Pokud vyhledáme hodnotu |ZT| / 2, trefíme se přesně mezi A a B.
Tím bychom dostali řešení v čase O(N log N), kde N je počet základen. Musíme vyzkoušet N možných umístění teleportéru, pro každé binárně vyhledat hranici mezi úseky a pak v konstantním čase spočítat M, přičemž si průběžně udržujeme nejlepší zatím nalezený výsledek.
Lineární řešení
Existuje ale i řešení v lineárním čase. Využívá následující pozorování: když posuneme teleportér doprava, mohou se A a B posunout také jen doprava (nebo zůstat na místě).
Na začátku umístíme teleportér do základny hned vedle hlavního sídla. Pak A=Z a B=T=Z+1. Budeme postupně posouvat T doprava a průběžně si udržovat čísla základen A a B. Po posunutí T musíme opravit pozici A a B. To uděláme jednoduše: dokud platí |ZB| < |ZT| / 2 (B leží v levé polovině spojnice ZT, tedy v úseku I), posuneme A i B o jednu základnu doprava.
Po jednom posunutí T se můžou A a B posunout i víckrát. Protože se ale posouvají jen doprava, za celý běh algoritmu dohromady se posunou maximálně N-krát, tedy jejich posouváním strávíme celkem čas O(N). Všechno ostatní (výpočet M a udržování průběžného minima) zvládneme v konstantním čase. Celkem si tedy vystačíme s časem O(N).
 30-3-4 Hmota a antihmota (Zadání)
30-3-4 Hmota a antihmota (Zadání)
Naším úkolem bylo oddělit hmotu a antihmotu aneb zjistit, jestli lze v rovině oddělit dvě množiny bodů přímkou tak, aby všechny body jednoho typu byly na jedné straně přímky a všechny body druhého typu na straně druhé.
Operovat se spoustou bodů přímo by ale bylo zbytečně složité, a tak si situaci trochu zjednodušíme použitím technik z odkazované kuchařky o geometrii. Uvědomíme si, že když nějaké dvě množiny bodů umíme oddělit pomocí přímky, umíme oddělit i jejich konvexní obaly (konvexní mnohoúhelníky obsahující všechny zadané body).
Spočítáme si konvexní obal bodů hmoty i antihmoty (což podle algoritmu z kuchařky umíme v čase O(N log N) – protože si body musíme setřídit podle nějaké souřadnice) a pak se zamyslíme, že mohla nastat jedna ze tří situací:
- Konvexní obaly se protínají – v takovém případě určitě body hmoty a antihmoty oddělit nelze.
- Konvexní obaly se neprotínají, ale hranice jednoho leží uvnitř druhého – tady také zjevně nelze body hmoty a antihmoty oddělit přímkou.
- Konvexní obaly se neprotínají a neleží v sobě – zde oddělovací přímka existuje.
Proč v posledním případě oddělovací přímka vždy existuje? Vezměme si jeden bod na obvodu konvexního obalu hmoty a druhý na obvodu konvexního obalu antihmoty takové, že jejich vzdálenost je nejmenší možná. Rozmyslete si, že to bez újmy na obecnosti je buď dvojice vrchol-vrchol, nebo vrchol-hrana.
Sestrojme úsečku spojující tyto dva nejbližší body a pak si vezměme osu této úsečky (nazvěme ji q) a rozmysleme si, že q určitě neprotíná ani jeden z konvexních obalů. Rozmyslíme si to pro obal hmoty, pro obal antihmoty to bude to samé: Pokud na straně hmoty je nejbližší bod vrchol, tak hrany z něj vycházející se od q určitě vzdalují a zároveň vymezují výsek roviny, ve kterém se celý konvexní obrazec nachází, takže k protnutí obrazce s q již určitě nedojde. A pokud je nejbližší bod na nějaké hraně, tak si rozmysleme, že úsečka spojující tento bod s nejbližším bodem druhého konvexního obalu bude kolmá na tuto hranu a q tak bude s touto hranou rovnoběžná. A protože hrana vymezuje polorovinu, ve které se celý konvexní obrazec musí nacházet, tak ani v tomto případě k protnutí obrazce s q určitě nedojde.
Dokázali jsme tak, že když se konvexní obrazce neprotínají a neleží v sobě, tak určitě existuje alespoň jedna oddělovací přímka. Než se zamyslíme, jak nějakou oddělovací přímku najít co nejrychleji, pojďme si spočítat, jak rychle umíme vyřešit samotnou otázku její existence.
Jak jsme si řekli výše, spočítání konvexních obalů nás bude stát čas O(N log N). Jak rychle umíme udělat test protnutí? Určitě bychom mohli zkusit každou hranu jednoho obrazce s každou hranou druhého, ale to by zabralo čas O(N2), což nechceme. Namísto toho se opět můžeme podívat do kuchařky a zjistit, že zde máme algoritmus hledající průsečíky úseček v rovině v čase O((N+P) log N) (kde P je počet průsečíků).
Nás budou zajímat průsečíky hran jednoho obalu s hranami druhého obalu a už jediný takový průsečík postačí ke zjištění, že se konvexní obaly protínají. Stačí tedy spustit algoritmus a zastavit ho okamžitě, jak na něco takového přijde. Můžeme tedy P shora odhadnout pomocí N a čas nám tak vyjde O(N log N) na tuto kontrolu.
Nakonec musíme ověřit, jestli se jeden konvexní obal nenachází celý uvnitř druhého. Vezmeme si tedy z každého konvexního obalu jeden bod a otestujeme, jestli se nenachází uvnitř konvexního obalu druhého obrazce, tento test zvládneme v O(N).
Pokud se nám konvexní obaly neprotínají a pokud se ani jeden z nich nenachází uvnitř druhého, tak můžeme oznámit, že oddělující přímka existuje. Vyřešili jsme tak lehčí verzi úlohy jenom s jedním obsáhlejším důkazem a s algoritmy z geometrické kuchařky v čase O(N log N).
Nalezení oddělovací přímky
Na úvod si povolme, že oddělovací přímka nám bude stačit i taková, která se některých bodů dotýká (pokud by nám to nestačilo, tak ji vždy můžeme posunout o dostatečně malé ε tak, aby se bodů nedotýkala). Příkladem může být čárkovaná přímka na obrázku.
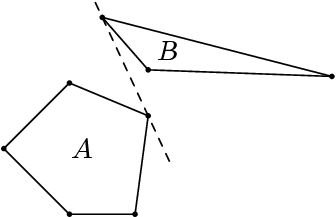
Teď se zamysleme, že když si vezmeme libovolnou oddělovací přímku dvou konvexních mnohoúhelníků, můžeme tuto oddělovací přímku pootočit (a posunout) tak, aby se každého z obrazců dotýkala v nějakém vrcholu. Náš cíl bude hledat právě takovéto oddělovací přímky, tedy přímky, které jsou prodloužením nějaké úsečky mezi nějakým vrcholem prvního a nějakým vrcholem druhého obrazce.
Pro vybranou dvojici vrcholů umíme rychle ověřit, jestli je jimi určená přímka oddělovací – pro každý z vrcholů si ověříme, jestli je v něm přímka tečnou (jen se obrazce v tomto bodě dotkne, ale nevstoupí do něj), nebo ne. Stačí nám ověřit, že je přímka oproti oběma hranám vycházejícím z tohoto vrcholu umístěná na stejné straně (pokud je, tak již nezasáhne ani do zbytku obrazce). Druhá podmínka, kterou oddělovací přímka musí splnit, je, že jeden konvexní mnohoúhelník se od ní nachází na jednu stranu a druhý na opačnou stranu. To umíme lehce ověřit tím, že si vybereme jeden bod z každého mnohoúhelníku a zjistíme, jestli leží na opačných stranách. Otestování tak umíme pro dvojici vrcholů vyhodnotit v konstantním čase.
Možných dvojic vrcholů je O(N2), takže při vyzkoušení všech možností bychom úlohu zvládli v čase O(N2), ale to nám stačit nebude.
Pojďme na to tedy jinak – na počátku si zvolíme libovolné dva vrcholy, každý z jednoho mnohoúhelníku, a natáhneme přímku mezi nimi. Když testem výše zjistíme, že není oddělovací, tak se po nějakém z mnohoúhelníků posuneme a zkusíme to znovu. Toliko postup v kostce, nyní podrobněji.
Pro vrchol a na mnohoúhelníku A a vrchol b na mnohoúhelníku B provedeme první pravidlo, které má splněné podmínky, a opakujeme:
- Pokud přímka určená a-b splňuje podmínky výše (neprotíná A ani B a A leží na opačné straně, než B), tak a-b vydáme jako řešení a skončíme.
- Pokud přímka určená a-b protíná A směrem od a k b, tak je a na
špatné straně A → posuneme a po směru hodinových ručiček na další
vrchol z A.
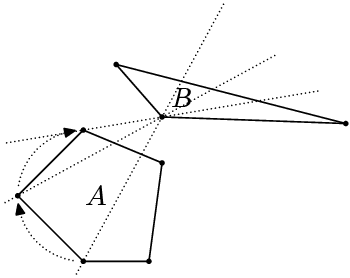
- To samé pro b a B.
- Pokud přímka určená a-b protíná A směrem od a dál → posuneme a po směru ručiček na další vrchol z A.
- To samé pro b a B.
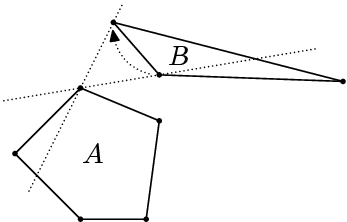
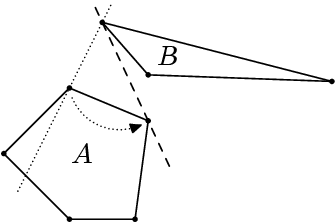
Pravidla 2 a 3 nám zaručí, že body na sebe „vidí“ (pokud na sebe přestanou vidět, tak „oběhnou“ svůj mnohoúhelník na druhou stranu). A pravidla 4 a 5 nám posunou přímku tak, aby byla pro každý z mnohoúhelníků tečnou.
Pokud oddělovací přímka existuje (což po kontrole z první části úlohy víme), tak náš algoritmus projde všechny možné kandidáty na ni. Dál po obvodu se posouváme jenom tehdy, pokud již víme, že na současné pozici oddělovací přímku nezkonstruujeme. Přitom maximálně jednou obkroužíme každý z obrazců, tato část je tedy lineární.
Společně s první částí umíme celou úlohu vyřešit v čase O(N log N).
 30-3-5 Rozbití skupin (Zadání)
30-3-5 Rozbití skupin (Zadání)
Úloha je podobná úloze 30-Z3-4 ze začátečnické kategorie, tak se inspirujeme jejím řešením. Dostali jsme řetězec x1,… ,xN, v němž jsou na některých pozicích „písmenka“ z P-prvkové abecedy a všude jinde mezery. Na místa mezer chceme vyplnit další písmenka tak, aby nikde nebylo více než M stejných písmenek vedle sebe.
Nejprve si rozmyslíme, jak bychom úlohu řešili, kdyby všude byly mezery. Budeme postupně počítat pro čím dál delší prefixy x1, … , xi čísla Aip. Ta nám budou říkat, kolika způsoby jde prefix vyplnit tak, aby končil písmenem p.
Odložme na chvíli, co dělat na úplném začátku. Představujme si, že už jsme v řetězci pokročili „dostatečně daleko“ a chceme spočítat nějaké Aip. Jak k tomu využít už známá Ai'p' pro i' < i?
Víme, že vyplněný prefix má končit písmenem p. To je součástí nějakého delšího souvislého p-ček, který má délku k ≤ M. Před tímto úsekem už musí ležet nějaké jiné písmeno p' (nebo začátek řetězce, ale to se nestane, protože jsme dostatečně daleko). Pro každé p' ≠ p tedy máme Ai-k,p' možností, jak vyplnit předchozí část prefixu, a za každou z nich můžeme připojit koncový úsek z k p-ček.
Sečteme tedy tyto možnosti přes všechny možné volby k a p' a dostaneme:
| M |
| k=1 |
Nyní vrátíme do hry možnost, že některá písmena jsou už předem daná. Tím pádem musíme při zvyšování k kontrolovat, zda xi-k+1 není předepsáno jako písmeno různé od p, a tehdy se zastavit. Může se samozřejmě stát, že se zarazíme hned o xi, takže celé Aip vyjde nulové.
Zbývá dořešit případ, kdy nejsme dostatečně daleko. Tehdy musíme počítat s tím, že i-k může prolézt před začátek řetězce. Pomůžeme si snadno: rozšíříme abecedu o nové písmeno Q a předvyplníme ho na pozici 0. Nové písmeno nebudeme vyplňovat nikam jinam. Nyní zjevně platí A0Q=1 a A0p=0 pro p ≠ Q. Výpočet všech ostatních Aip se pak vždy zarazí o začátek řetězce a správně započítáme jednu možnost, protože začít se dá jedním způsobem.
K vyřešení úlohy nám tedy stačí spočítat všechna Aip a pak sečíst Anp přes všechna p. Jak dlouho to bude trvat? Všech Aip je O(NP), při výpočtu každého z nich sčítáme O(MP) čísel. Časová složitost tedy činí O(NP2M).
Zrychlujeme…
Několika jednoduchými úpravami můžeme algoritmus ještě zrychlit. Především se zbavíme druhé sumy ve výpočtu Aip. K tomu si předpočítáme čísla Ti = Ai1 + Ai2 + … + Aip a všimneme si, že druhá suma je rovna Ti-k - Ai-k,p. (Druhá suma vždy z P členů součtu Ti jeden vynechává, tak ho prostě od Ti odečteme.)
Tím pádem spočítat jedno Aip trvá pouze O(M), takže jedno i zpracujeme v čase O(PM). Do toho se jistě vejde čas O(P) potřebný na spočítání Ti. Vida, celý algoritmus jsme zrychlili na O(NPM).
Nyní vytáhneme z rukávu další trik. Představte si, že bychom se dozvěděli, kam až se zvýší k v první sumě, než se zarazíme o předepsaný znak různý od p. Označme tuto hodnotu K. Počítáme tedy
| Aip | = ∑
| ||||
= (∑
|
To jsou nějaké dvě sumy souvislých úseků posloupností, které zvládneme spočítat v konstantním čase, pokud si pro tyto posloupnosti budeme udržovat prefixové součty.
Aby tento trik fungoval, musíme ovšem znát K. Ukážeme, že si můžeme dovolit přepočítávat při každém prodloužení prefixu zarážky – čísla Zp, která nám budou říkat, na které pozici leží poslední nemezerové písmenko různé od p. Udržování je snadné: kdykoliv prodloužíme prefix o nějaké písmenko p, přenastavíme všechny zarážky Zp' pro p' ≠ p na aktuální pozici i. Pokud prodloužíme o mezeru, zarážky zůstanou stejné.
Rozmysleme si, kolik práce vykonáváme při každém z N prodloužení prefixu. Nejprve přepočítáme zarážky, to trvá O(P). Pak pro každé p počítáme Aip v konstantním čase, celkem tedy zase O(P). Každé Aip také připočítáme k Ti, což nám čas nezhorší. Nakonec aktualizujeme všechny prefixové součty; ty udržujeme pro P+1 různých posloupnost (jedna z nich je T), a to opět stihneme v O(P).
Tím jsme získali algoritmus s časovou složitostí O(NP).
Poznámka o samých mezerách
Dovolíme si krátkou poznámku na závěr: Jak by se úloha chovala, kdyby v zadaném řetězci byly jenom mezery? Tehdy by hodnota Aip evidentně nezávisela na p, takže by stačilo počítat Ai1. Druha suma by tedy sčítala P-1 stejných členů a dostali bychom:
| M |
| k=1 |
| M |
| k=1 |
To je nějaká lineární rekurence, na kterou by se dal pro konkrétní P a M vymyslet explicitní vzoreček, do nějž bychom rovnou dosadili i a vypadlo by řešení. Například pro P=M=2 vyjdou známá Fibonacciho čísla.
 30-3-6 Střežení oblasti (Zadání)
30-3-6 Střežení oblasti (Zadání)
Na této úloze není nic příliš záludného – jednoduše stačí příkazy odsimulovat. Už však záleží na tom, jaké datové struktury přitom využijeme.
Hranice se v každém čase skládá z několika navzájem se nepřekrývajících hlídaných intervalů – souvislých úseků, jejichž celý vnitřek je hlídaný a jejichž krajní body hraničí s nehlídanými oblastmi. Takové intervaly můžeme v programu reprezentovat jako dvojice (začátek, konec). Právě na počet hlídaných intervalů po každé operaci se úloha ptá.
Pořídíme si tedy nějakou datovou strukturu, ve které si budeme udržovat všechny intervaly a po každé operaci ji odpovídajícím způsobem upravíme. Pro začátek budeme skromní a intervaly budeme v nějakém libovolném pořadí udržovat v poli.
Co udělají obě operace s naším polem?
- Hlídej (A, B): všechny intervaly překrývající se s (A, B) se slijí do jednoho intervalu. Ten bude začínat v nejlevějším z jejich začátků (popř. A, pokud je A ještě více nalevo) a končí v nejpravějším z jejich konců (popř. B). V naší reprezentaci nám stačí pole projít, smazat právě všechny intervaly zasahující do (A, B) a pak přidat na konec nový interval (A', B') odpovídající jejich „slití“.
- Přestaň hlídat (A, B): intervaly ležící plně v (A, B) zmizí, intervaly částečně zasahující do (A, B) se z jedné strany oříznou a intervaly zcela obsahující (A, B) se rozdělí na dva. Opět stačí pole projít a změnit pouze intervaly mající překryv s (A, B).
Rozmyslete si, že to, zda se dva intervaly překrývají, umíme ověřit v konstantním čase. Celkový počet intervalů si také jistě umíme udržovat v konstantním čase.
Toto řešení má paměťovou složitost O(N) a časovou složitost O(N2), kde N je počet operací. Každá operace totiž vytvoří maximálně jeden interval, takže po N operacích jich můžeme mít nejvýše N. Když nebudeme operace provádět hloupě (např. nebudeme všechny intervaly zasahující do (A, B) mazat po jednom v O(N), ale smažeme je všechny najednou), budou obě operace trvat O(N).
Rozmyslíme si, že v průměru po každé operaci přidáme, změníme a odstraníme jen konstantně mnoho intervalů. Proč tomu tak je? V obou operacích odstraňujeme libovolně mnoho intervalů, ale přidáváme jich vždy jen konstantně mnoho. Abychom ale mohli mazat, musíme mít co, tedy pokud jsme provedli k mazání, muselo před nimi následovat aspoň k přidání. Víme však, že přidání je dohromady O(N), tedy i mazání je O(N) a průměrný počet mazání na jednu operaci je konstantní.
Zrychlujeme
To, že každá operace v průměru změní jen konstantně intervalů, naznačuje, že by mohlo existovat i nějaké rychlejší řešení. To naše je pomalé hlavně kvůli tomu, že prochází hromadu intervalů, které pro danou operaci nejsou nijak zajímavé.
Pojďme ho upravit. Začneme stejně, s polem uchovávajícím jednotlivé intervaly. Tentokrát v něm však intervaly budou uspořádané vzestupně podle svých začátků. Díky tomu budeme v poli umět binárním vyhledáváním najít nejlevější a nejpravější interval, které nás pro danou operaci zajímají a budeme moci měnit jen intervaly mezi nimi. Obě operace nám pak postačí upravit tak, aby uspořádání zachovávaly – stačí všechna vkládání provádět nikoliv na konec, ale na místo určené dalším binárním vyhledáváním. Odstranění jistě uspořádání neporuší a úprava intervalu jde nahradit kombinací odstranění a vkládání.
Problém s takovým řešením je, že je úplně stejně pomalé jako to předchozí. Na nalezení správného místa sice používáme binární vyhledávání, ale všechno si pokazíme vkládáním do pole, jelikož už tentokrát nevkládáme jeho konec, ale do jeho prostředka, což samozřejmě trvá O(N). Nabízí se použít spojové seznamy, které umí vkládat v O(1). V těch však zase neumíme rychle binárně vyhledávat, protože jen s ukazatelem na první prvek neumíme rychle najít tolik potřebný prostředek.
Zachrání nás vyhledávací stromy. Pokud jste o nich ještě neslyšeli, můžete si přečíst naši kuchařku, ve které popisujeme, k čemu taková datová struktura je a jak může vypadat uvnitř. Pro popis řešení stačí vědět, že binární vyhledávací stromy umí udržovat uspořádanou množinu a v O(log N) nad ní provádět operace „přidej prvek do množiny“, „odeber prvek z množiny“ a „vrať nejmenší prvek z množiny větší než x“.
Stačí tedy, když v předchozím řešení vyměníme pole za nějaký vyhledávací strom (ve kterém opět řadíme intervaly podle jejich začátku), a dostaneme řešení pracující v čase O(N log N).
Na závěr malá poznámka: i řešení se spojovými seznamy by šlo upravit, aby v průměru běželo v O(N log N), takové randomizované struktuře se říká skip list. Hrubá myšlenka je taková, že každé buňce spojového seznamu kromě odkazu na následníka náhodně přidáme ještě několik zkratkových odkazů, každý další odkaz ukazující zhruba dvakrát dál než předchozí. Při vkládání prvku na správné místo si pak zkratkami urychlujeme čas a v průměru nám nalezení správného místa trvá O(log n). Více si o skip listech můžete přečíst například na anglické Wikipedii.
 30-3-7 Funkce očima assembleru (Zadání)
30-3-7 Funkce očima assembleru (Zadání)
Úkol 1: Třetí největší číslo
Hledání třetího největšího čísla můžeme napsat podobně jako třídění
vkládáním. V registrech r3 až r5 si budeme udržovat
první až třetí největší číslo. Na začátku všechna tři inicializujeme
na nuly. Pak z paměti načítáme prvky posloupnosti jeden po druhém
a zatřiďujeme je mezi tři největší čísla. To se dá hezky popsat pomocí
podmíněných instrukcí MOV.
Program je přímočarý, jen si musíme dávat pozor na volací konvenci:
počet čísel dostaneme v r0, adresu prvního čísla v r1,
registry od r4 výše musíme vrátit do původního stavu a z funkce
se vracíme pomocí BX lr.
max3:
PUSH {r4-r6}
MOV r3, #0 @ r3 = zatím největší číslo
MOV r4, #0 @ r4 = druhé největší
MOV r5, #0 @ r5 = třetí největší
dalsi:
LDR r2, [r1], #4 @ r2 = aktuální číslo
CMP r2, r3 @ vyměníme za r3?
MOVHS r6, r3
MOVHS r3, r2
MOVHS r2, r6
CMP r2, r4 @ vyměníme za r4?
MOVHS r6, r4
MOVHS r4, r2
MOVHS r2, r6
CMP r2, r5 @ vyměníme za r5?
MOVHS r5, r2
SUBS r0, #1 @ snížíme počítadlo
BNE dalsi
MOV r0, r5 @ vrátíme třetí největší
POP {r4-r6}
BX lr
Úkol 2: Nulování paměti
Jak vynulovat blok paměti co nejméně instrukcemi? K tomu se hodí instrukce
MOVHS – ta umí zapsat do paměti hned několik registrů najednou. My si
uvolníme registry r2 až r12, naplníme je nulami a pokaždé zapíšeme
všechny najednou.
Než se do toho pustíme, musíme ovšem zařídit, aby adresa nulované paměti byla dělitelná čtyřmi. A když už bude zbývat méně než 44 bajtů, je potřeba „včas sundat sedmimílové boty“ a zbytek vynulovat citlivěji (v našem případě po bajtech). Zbývá poslední detail: ošetřit případy, kdy je celý zadaný blok příliš krátký – tehdy rovnou přepneme na nulování po bajtech.
nuluj:
MOV r2, #0 @ r2 bude vždy 0
CMP r1, #48 @ příliš krátký blok
BLO pomalu
zarovnej: @ adresu zarovnáme na 4 B
ANDS r3, r0, #3
BEQ rychle
SUB r1, #1
STR r2, [r0], #1
B zarovnej
rychle: @ r2-r12 budou nuly
PUSH {r4-r12}
MOV r3, r2
MOV r4, r2
@ ... podobně do r5 až r12
SUB r1, #43
rychleee: @ nulujeme najednou 44 B
STMIA r0!, {r2-r12}
SUBS r1, #44
BHS rychleee
ADD r1, #43
POP {r4-r12}
pomalu: @ zbylých nejvýše 48 B
STR r2, [r0], #1
SUBS r1, #1
BNE pomalu
BX lr
Jak rychle nulujeme? Na jeden průchod hlavní smyčkou (od návěští rychleee)
vynulujeme 44 bajtů a stojí nás to 3 instrukce. Nulujeme tedy 44/3 ≐14.67
bajtu za instrukci. Režie zbylých dvou smyček (zarovnávací a koncové) je shora omezena
nějakou konstantou, takže pro velké bloky je zanedbatelná.
Všimněte si ale, ze tří instrukcí v hlavní smyčce jenom jedna nuluje paměť, zatímco zbylé dvě se starají, aby smyčka běžela a včas se zastavila. Pouze třetinu instrukcí tedy spotřebujeme na užitečnou práci, zbytek je režie smyčky. Tento poměr můžeme zlepšit tak, že několik iterací smyčky sloučíme do jedné, třeba takto:
rychleeeee:
STMIA r0!, {r2-r12}
STMIA r0!, {r2-r12}
STMIA r0!, {r2-r12}
SUBS r1, #132
BHS rychleeeee
Nyní v jedné iteraci smyčky provedeme celkem 5 instrukcí, z nichž 3 jsou výkonné a stále 2 režijní. Poměr se tedy zlepšil z 1/3 na 3/5. Za jednu iteraci nyní vynulujeme 132 bajtů, takže rychlost jsme zvýšili na 132/5 = 26.4 bajtu na instrukci. Takto se můžeme libovolně přiblížit k teoretickému maximu 44 bajtů na instrukci, ovšem platíme za to tím, že pro malé bloky se efektivita programu snižuje.
Mimochodem, kombinování více iterací do jedné je standardní technika, kterou například překladače Céčka běžně dělají. Říká se jí loop unrolling, nebo česky rozbalování smyček.
Úkol 3: Součet argumentů
Sčítání všech argumentů až do prvního nulového je jednoduché, jen se musíme poprat
s tím, že první 4 argumenty dostaneme v registrech, zatímco zbývající na zásobníku.
Přitom předem nevíme, kolik jich celkem bude. Pomůžeme si snadno: argumentové registry
r0-r3 hned uložíme na zásobník, čímž zařídíme, že všechny argumenty budou uloženy
na zásobníku pěkně za sebou, a tak je odtamtud jeden po druhém přečteme. Ve skutečnosti
je lepší první argument nechat v registru r0 a k tomuto registru pak přičítat
všechny ostatní argumenty. To je současně registr, ve kterém máme vrátit výsledek.
soucet_arg:
CMP r0, #0 @ součet 0 argumentů je 0
BEQ hotovo @ v r0 bude výsledek
PUSH {r1-r3} @ argumenty 2 až 4 na zásobník
MOV r1, sp
znovu: @ procházíme zásobník
LDR r2, [r1], #4
ADD r0, r2
CMP r2, #0
BNE znovu
POP {r1-r3} @ uklidíme zásobník
hotovo:
BX lr
Úkol 4: Nebudu si číst pod lavicí…
Nechat programátora, ať za trest něco napíše stokrát, jak známo potrestá spíš jeho
učitele. Stačí ve smyčce volat printf podle volací konvence. Jediné, na co bychom
se mohli nachytat, je, že funkce mají dovoleno přepsat registry, v nichž dostaly argumenty,
takže si je nesmíme zapomenout uložit.
LDR r0, =trest @ r0 = formátovací řetězec
MOV r1, #1 @ r1 = počítadlo
otrocina:
PUSH {r0,r1}
BL printf
POP {r0,r1}
ADD r1, #1
CMP r1, #100
BLS otrocina
B konec
trest:
.ASCII "%d. Nebudu si číst pod lavicí"
.BYTE 10, 0 @ konec řádku, konec řetězce
.ALIGN 4
konec:
Úkol 5: Ohackované printf
Zlatým hřebem tohoto dílu seriálu bylo upravit printf, aby číslovalo
řádky. Nabízí se vyměnit všechna volání printf za volání nějaké naší
funkce. Tomu brání zdánlivá maličkost: neumíme všechna volání najít.
Půjdeme na to chytřeji: přepíšeme první instrukci funkce printf na skok
do naší vlastní funkce. Naše funkce vypíše číslo řádku a následně vypíše to, kvůli
čemu byla zavolaná. Na obojí se hodí zavolat původní printf. To zařídí funkce
orig_printf, která nejprve provede první instrukci původního printf
(tu, kterou jsme přepsali skokem) a pak skočí na zbytek původního printf.
Jediný další chyták je, že v kódu instrukce skoku je cílová adresa uložena
relativně (32-bitová absolutní adresa by se do 4 bajtů instrukce nevešla).
Nemůžeme tedy instrukci zkopírovat z jiného místa v programu. To by se dalo
obejít zkonstruováním adresy v registru a BX na tento registr, ale pak bychom
si nevystačili s přesunutím jediné instrukce. Radši se tedy naučíme, jak se
instrukce skoku kóduje (to najdeme v popisu instrukční sady ARMu, nebo se
prostě v simulátoru podíváme, jak jsou různé skoky zakódované).
Pokud na adrese x leží instrukce B y, uložíme do ní, že má skákat
o (y-x-8)/4 dopředu. Osmičku odečítáme proto, že se snaží mít rozpracovaných
několik instrukcí v předstihu, takže v okamžiku vykonávání instrukce z adresy x
je v registru pc (r15) už hodnota x+8. Navíc adresy instrukcí jsou
vždy dělitelné čtyřmi, takže nejnižší dva bity rozdílu jsou vždy nulové a není je
potřeba ukládat. Kód instrukce skoku má pak ve svých horních 8 bitech uloženo
0xea a ve zbylých 24, o kolik dopředu skáče (záporná čísla ukládá ve dvojkovém
doplňku). Kód tedy v programu snadno spočítáme.
printf_hack:
@ Zkopírujeme 1. instrukci printf
LDR r1, =printf
LDR r2, =orig_printf
LDR r0, [r1]
STR r0, [r2]
@ Nahradíme ji skokem na fake_printf
LDR r0, =fake_printf
SUB r0, r1
SUB r0, #8 @ kompenzace posunu pc
LSL r0, #6 @ dělení 4 a současně nulování
LSR r0, #8 @ horních 8 bitů
ORR r0, #0xea000000 @ horních 8 bitů
STR r0, [r1]
B konec
@ Toto je ekvivalentní s původním printf
orig_printf:
.WORD 0 @ sem přijde 1. instrukce printf
B printf+4 @ pokračování původního printf
@ Tímto printf nahradíme
fake_printf:
PUSH {r0,r1,lr}
LDR r0, =pocitadlo @ Zvýšíme počítadlo o 1
LDR r1, [r0]
ADD r1, #1
STR r1, [r0]
LDR r0, =zprava @ Vypíšeme ho
BL orig_printf
POP {r0,r1,lr} @ Vypíšeme, co chtěl volající
B orig_printf
pocitadlo:
.WORD 0
zprava:
.ASCIIZ "%d: " @ zkratka za .ASCII + .BYTE 0
.ALIGN 4
konec: