Pátá série třicátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 30-5-1: Úklid po soustředku
- 30-5-2: Útěk z trezorů
- 30-5-3: Energetické úspory
- 30-5-4: Kartotéka
- 30-5-5: Výroba likvidátoru
- 30-5-6: Nápověda na lyžích
 30-5-1 Úklid po soustředku (Zadání)
30-5-1 Úklid po soustředku (Zadání)
Máme najít cestu v bludišti, tak bychom na to mohli jít nějakým prohledáváním grafu. Mohli bychom třeba zkusit všechny velikosti vozíku a vzít tu největší, se kterou jde bludiště projít. Na to ale budeme určitě potřebovat zjišťovat, jestli se nám vozík vejde na konkrétní políčko. Kdybychom to dělali naivně – pokaždé kontrolovali, jestli jsou volná všechna políčka, na kterých je vozík – tak by nám to nepříjemně zhoršilo časovou složitost. Vozík může být řádově stejně velký jako celá mapa, takže by jedno zkontrolování stálo O(M2) času.
Mnohem lepší bude si pro všechna políčka předpočítat, jak velký vozík se tam vejde (jak velký může být vozík s levým horním rohem v daném políčku). Půjdeme postupně od spodní strany zprava. Spodní řádek mapy je jednoduchý: tam, kde je políčko volné, bude maximální velikost vozíku 1, jinak to bude 0. V dalším řádku se vždy podíváme jak velké vozíky se vejdou na políčko o jedna dolů, na políčko o jedna vpravo a na políčko o jedna vpravo dolů. Vezmeme si velikost vozíku, který se vejde na všechna z nich, to bude minimum z těch třech čísel. Na aktuální políčko se nám tak akorát vejde vozík o jedna větší. Pro každé políčko se tedy podíváme na políčko vpravo, vpravo-dole a na políčko dole, vezmeme z nich minimum, přičteme jedničku a zapíšeme. Celou mapu takto projdeme v čase O(MN), kde M a N jsou její rozměry. Při dotazu na velikost se stačí v konstantním čas jednoduše podívat na jedno políčko.
Kdybychom teď chtěli najít nejkratší cestu pro konkrétní velikost vozíku, stačí použít běžné prohledávání do šířky, přičemž políčko budeme považovat za průchozí, pokud se na něj vozík vejde (podle toho, co jsme si předpočítali). To stihneme v lineárním čase vzhledem k počtu políček. Navíc funguje, že když projdeme s nějak velkým vozíkem, tak to půjde i se všemi menšími, a tak můžeme na maximální možnou velikost vozíku použít binární vyhledávání. Když si označíme A velikost vozíku, která se vejde na začátek, budeme půlit interval [0, A] a celé to bude potřebovat O(MN log A) času a O(MN) paměti.
Sice už to nezrychlíme víc než o logaritmus A, ale proč to neudělat, když můžeme. V principu začneme prohledávat graf do šířky s největším vozíkem, který se vejde na začátek, ale políčka, na která se nevejdeme, nebudeme úplně zahazovat. Místo toho si pro ně na začátku vyrobíme A front, jednu pro každou velikost, a budeme používat tu pro největší vozík. Když narazíme na políčko, jehož předpočítaná velikost vozíku je menší, přidáme poličko do fronty, která odpovídá této menší velikosti vozíku. Pokud se dostaneme do cíle (nebo se spíš cíl dostane pod vozík), můžeme prohlásit, že cesta s daným vozíkem určitě existuje, a skončit.
Když nám fronta dojde, smíříme se s tím, že s takto velkým vozíkem cesta do skladu nevede, a zkusíme vozík o jedna menší. Prázdnou frontu zahodíme a začneme používat tu určenou pro o jedna menší vozík. Tímto jsme plynule přešli na prohledávání s menším vozíkem. Všude, kam se dalo dostat s původním vozíkem, se dostaneme i s menším, takže můžeme všechno nalezené použít znovu. V průběhu celého algoritmu tento přechod provedeme maximálně A-krát, a každý nás bude stát jen konstantně času. Celkově každé políčko vytáhneme z fronty jen jednou a pokaždé na něm uděláme jen konstantně práce (projdeme 4 okolní), takže celý algoritmus doběhne v čase O(MN).
Drobný problém je, že výše uvedený postup nám nemusí dát nejkratší cestu, jenom nám řekne, pro jak velký vozík ještě cesta existuje. To ale snadno obejdeme tak, že pro ten největší možný vozík spustíme běžné prohledání do šířky popsané výše. To také doběhne v lineárním čase a složitost nám tak nezhorší.
 30-5-2 Útěk z trezorů (Zadání)
30-5-2 Útěk z trezorů (Zadání)
Na jaké políčko chceme položit bombu? Především musí být dosažitelné ze startu. Současně také oblast, kterou bomba vybourá, buďto musí obsahovat políčko dosažitelné z cíle, nebo aspoň s takovým políčkem musí sousedit. Nějaké políčko dosažitelné z cíle tedy musí být v „obdélníku s ušima“ okolo políčka s bombou:
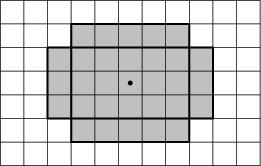
Zbytek je už technické cvičení na základní algoritmy. Dvojím prohledáním do šířky zjistíme, která políčka jsou dosažitelná ze startu a která z cíle. Pak si předpočítáme dvojrozměrné prefixové součty, pomocí nichž půjde v konstantním čase zjistit, kolik políček dosažitelných z cíle leží v daném obdélníku. A nakonec si uvědomíme, že každý ušatý obdélník je sjednocením pěti disjunktních obdélníků bez uší.
Celkově tedy strávíme čas O(RS) předvýpočty a pak pro každé z RS políček v konstantním čase rozhodneme, zda je užitečné umístit tam bombu. Časová složitost algoritmu tedy činí O(RS).
 30-5-3 Energetické úspory (Zadání)
30-5-3 Energetické úspory (Zadání)
Většina z vás úlohu řešila tak, že si našla nejkratší cestu mezi dvěma ze zadaných křižovatek a poté se k ní pokoušela připojit třetí křižovatku. Řešení by to bylo pěkné, nebýt chybného předpokladu, že hledaná podmnožina hran musí obsahovat nejkratší cestu mezi některými význačnými vrcholy. Jeden protipříklad můžete najít na obrázku níže: nejkratší cesty mezi význačnými vrcholy A, B a C jsou strany trojúhelníku ABC, ale nejmenší podmnožina hran, po kterých se dá dojít do všech tří význačných vrcholů, obsahuje hrany AX, BX a CX.
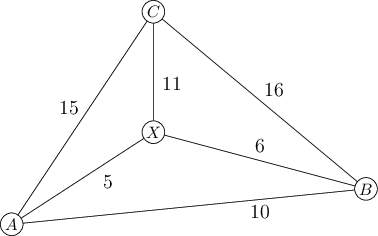
Zajímavé je pozorování, že ačkoliv nám řešení pomocí dvou nejkratších cest nedá vždy nejmenší množinu hran, nemůže být o mnoho horší než optimum. Přesněji, součet délek dvou nejkratších cest mezi vrcholy A, B a C je maximálně o třetinu delší než nejmenší podmnožina hran. Plyne to z toho, že cesty přes X jsou vždy stejně dlouhé nebo delší než nejkratší cesty. Dostaneme tři nerovnosti:
| |AX| + |XB| | ≥ |AB|, |
| |BX| + |XC| | ≥ |BC|, |
| |CX| + |XA| | ≥ |CA|. |
Níže dokážeme, že hledaná nejmenší podmnožina je tvořena cestami z každé význačné křižovatky do X. Sečtením těchto tří nerovností tedy dostaneme dvojnásobek délky nejmenší podmnožiny:
Nyní vybereme nejdelší ze tří nejkratších cest (na obrázku BC) a vyjádříme ji pomocí zbylých dvou:
| |AB|+|CA| |
| 2 |
Obě nerovnosti zkombinujeme a získáme nerovnost
| 2 · (|AX| + |BX| + |CX|) ≥ |AB| + |BC| + |CA| ≥ | |
| ≥ |AB| + |CA| + (|AB|+|CA|)/2 = | |
| = 3/2 · (|AB|+|CA|), |
ze které vidíme, že součet dvou nejkratších cest je nejvýše 4/3 délky nejmenší podmnožiny hran. Z tohoto důvodu jsem tedy i za toto řešení udělovala nějaké body.
Správné řešení
Jak jsem již naznačila, musíme najít nějaký bod X, ze kterého vedou „krátké“ cesty do A, B i C. Takový bod určitě existuje. V hledané nejmenší množině hran totiž musí být cesta (ne nutně nejkratší) mezi body A a B. Zároveň se musíme umět dostat i do bodu C, z bodu C tedy musí vést nějaká cesta, která se napojuje na cestu mezi A a B. Bod napojení označíme jako X (může být shodný i s některým z bodů A, B nebo C). Protože hledáme nejmenší podmnožinu, musíme najít takové X, které bude mít součet vzdáleností k A, B a C nejmenší. Jak to udělat? Mohli bychom z každého bodu grafu spustit prohledávání a spočítat součet těchto vzdáleností, ale to by bylo pomalé. Místo toho na to půjdeme obráceně: spočítáme nejkratší vzdálenosti z bodů A, B a C do všech ostatních bodů grafu.
Spustíme postupně Dijkstrův algoritmus z A, B i C a u každého bodu si zapamatujeme všechny tři vzdálenosti. Poté projdeme celý graf ještě jednou a najdeme bod, který bude mít součet těchto vzdáleností nejmenší. Hledaná podmnožina hran jsou pak hrany tvořící nejkratší cestu z nalezeného bodu X do A, B a C. Tyto nejkratší cesty můžeme najít třeba tak, když si u každého bodu zapamatujeme kromě vzdálenosti i bod, ze kterého jsme přišli. Poté cestu budeme umět zrekonstruovat.
Dijkstrův algoritmus spustíme pouze třikrát, výsledná časová složitost tedy bude stejná jako složitost tohoto algoritmu: O((M+N) log N). Paměťová složitost bude O(M+N), protože nám stačí pamatovat si graf a konstantně mnoho informací u každého vrcholu.
 30-5-4 Kartotéka (Zadání)
30-5-4 Kartotéka (Zadání)
Na vstupu jste dostali dva spojové seznamy (tak se říká struktuře ze zadání) a měli jste za úkol nalézt, kde „srůstají“. Jenže tentokrát jste měli k dispozici jen konstantní množství paměti a bylo tedy potřeba nad problémem přemýšlet z trochu jiného úhlu.
Jako vždy, pokud nevíme, jak začít, tak se vyplatí základní řešení – vyzkoušet všechny možnosti. Tedy postupně půjdeme prvek po prvku v prvním seznamu a vždy se zeptáme, zda se vyskytuje i ve druhém. První takový je místem srůstu. A jak zjistit, že se prvek vyskytuje v druhém seznamu? Nejjednodušší způsob je projít druhý seznam prvek po prvku a každý s ním porovnat. Tedy za každý prvek v prvním seznamu projdeme celý druhý seznam a dostaneme tak časovou složitost O(NM) (kde N a M jsou délky seznamů). Do konstantní paměťové složitosti jsme se jistě vešli.
Pojďme toto řešení vylepšit. Často, když hledáme nějaké místo v posloupnosti, tak se nabízí využít binární vyhledávání. Tedy místo abychom se ptali postupně každého prvku prvního seznamu jestli je i ve druhém, tak se nejprve zeptáme na tuto otázku prostředního prvku. Všimněte si, že není problém prostřední prvek najít. Stačí spočítat délku seznamu (tak, že jej projdeme a přičteme jedničku za každý prvek) a pak tuto délku vydělíme dvěma. Výsledkem je počet prvků, které musíme projít od začátku seznamu abychom se dostali do jeho středu.
Jak nám odpověď pomůže? Víme, že pokud se tento prvek nachází i ve druhém seznamu, tak „místo srůstu“ je nejpozději v tomto prvku. Zbylé prvky seznamu tedy jistě můžeme zahodit. Naopak pokud tento prvek ve druhém seznamu není, tak „srůst“ nastává až za tímto prvkem. Tedy můžeme naopak zahodit všechny prvky z prvního seznamu až do tohoto prvku. Tak jako tak se vždy zbavíme poloviny prvků v seznamu. Pak už jen opakujeme celou tuto proceduru jen místo celého prvního seznamu budeme uvažovat jeho zkrácenou verzi. Opakujeme tolikrát, dokud nám z prvního seznamu nezbude jediný prvek, tento prvek je jistě místem „srůstu“.
Jelikož vždy půlíme velikost seznamu, celkem opakujeme log N kroků. Pro každý krok musíme stále projít celý druhý seznam, dostáváme tedy časovou složitost O(M log N).
Všimněte si, že v každém kroku půlíme jeden seznam. Nic nás ale nenutí vždy vybírat ten stejný. Intuice nám tedy velí vybrat vždy ten seznam, který je aktuálně (po zahození prvků) větší, protože se tím zbavíme většího počtu prvků.
Pomůže nám to ale? Ukážeme, že ano. Označme K součet prvků v obou seznamech. V prvním kroku musíme projít všech těchto K prvků. Spočítejme ale, kolik z nich zahodíme. Delší seznam má délku alespoň K/2 a polovinu z něj zahodíme, tedy alespoň K/4. Jinými slovy nám pro další krok zbude 3/4 K prvků. Pro následující krok pak tři čtvrtiny z těchto tří čtvrtin, tedy (3/4)2 K. A tak dále, pokaždé zmenšíme počet prvků na tři čtvrtiny (nebo méně).
V každém kroku musíme jen projít všechny nezahozené prvky, takže časová složitost bude nanejvýš:
Řešení s nápadem
Uff… Dostali jsme lineární řešení, a pokud jste zběhlí v programátorských praktikách a základech matematické analýzy, tak vám možná přišlo i příjemně přímočaré. Pro ty ostatní z vás, kterých je (podle došlých řešení) většina, ale nabízíme jiné řešení. Toto řešení sice vyžaduje nejprve na problém „koukat“, ale odměnou je elegantnější a stále optimální řešení.
Představme si, že bychom u každého prvku v obou seznamech znali jeho vzdálenost k profesorovi. Všimněte si, že pro prvky, které jsou v obou seznamech je tato vzdálenost stejná, bez ohledu na to, z pohledu kterého seznamu se na něj díváme. To nám dává jednoduchý nástroj, jak poznat, zda je prvek v obou seznamech. Stačí se u daného prvku podívat na jeho kamaráda z druhého seznamu, který má stejnou vzdálenost k profesorovi. Prvky, které jsou jen v jednou seznamu, mají nějakého jiného kamaráda v druhém seznamu. Naopak prvky, které jsou v obou seznamech se kamarádí… sami se sebou.
Jenže na pamatování si těchto čísel nemáme paměť. Všimněme si ale, že pokud známe nějakou dvojici kamarádů, tak snadno poznáme kamarády, všech jejich následníků (jsou-li A a B kamarádi, následník A se kamarádí s následníkem B). Stačí tedy najít první dvojici kamarádů (první prvky delšího seznamu jsou zcela bez kamarádů).
Jak tuto dvojici najdeme? Nejprve si spočítáme délku obou seznamů (N, M). Předpokládejme, že řetězec délky N je ten kratší. U delšího řetězce pak musíme ze začátku zahodit tolik prvků o kolik je tento řetězec delší. Tedy formálněji ze začátku delšího řetězce se posuneme o M-N prvků níže. Vzdálenost prvku, který dostaneme, k profesorovi je pak M-(M-N) = N. Takže se kamarádí se začátkem druhého seznamu. Teď stačí porovnat tyto dva prvky, pokud jsou různé, tak se přesuneme na jejich následníky (kteří jsou také kamarádi), zkontrolujeme, zda se nerovnají oni atd. Toto opakujeme, dokud se nedostaneme na první prvek, jenž se kamarádí sám se sebou. Tento prvek je pak místem srůstu.
Jelikož jsme každý prvek prošli jen dvakrát, tak časová složitost je opět lineární. Pamatujeme si vždy jen pár prvků a několik hodnot, takže jsme se vešli i do konstantní paměti.
Velikost konstantní paměti
Možná máte pocit, že jsme v řešeních trochu podváděli. Pamatovali jsme si vždy jen pár čísel, ale ne jen ledajakých čísel. Konkrétně jsme si potřebovali pamatovat velikost řetězců, což je ale číslo závislé na vstupu, takže by se do konstantní paměti vejít nemělo!
V řešení jsme jen zmínili, že máte konstantní množství pomocné paměti a dále to neupřesnili, za což se omlouváme. Obvykle konstantní množství paměti chápeme v KSP jako konstantní množství buněk, kde každá buňka je schopná uchovat číslo ze vstupu.
Proč je takováto představa rozumná? Zejména pokud u druhé varianty řešení se můžete šikovnou manipulací s ukazateli zcela vyhnout potřebě pamatovat si takové číslo? Všimněte si, že v řešení zcela automaticky pracujeme s ukazateli na karty (a uchováváme si je). Ukazatel musí být pro každou kartu zcela jiný. Máme-li K karet, musí každý ukazatel zabírat alespoň log K bitů paměti. A v této paměti si už pohodlně můžeme uchovávat i velikosti řetězců. Kdybychom měli skutečně jen pár bitů, nebyli bychom schopní udělat vůbec nic, jelikož bychom si ani nemohli pamatovat kartu, se kterou pracujeme.
 30-5-5 Výroba likvidátoru (Zadání)
30-5-5 Výroba likvidátoru (Zadání)
Pro stručnost budeme v textu řešení pro největšího společného dělitele (NSD) čísel a a b používat (vymyšlené) značení a⋄b. To, že tato notace připomíná třeba značení operace sčítání nebo násobení, není náhoda – ve skutečnosti se na ⋄ můžeme dívat taky jako na nějakou operaci, která vezme dvě čísla a nějak je „zkombinuje“ do nového.
Vzoreček z kuchařky pro NSD více čísel a1,… ,an v této notaci můžeme napsat jako a1⋄(a2⋄(… (an-1⋄an))… ). Když si uvědomíme, jak funguje školní algoritmus na počítání NSD pomocí prvočíselného rozkladu, zjistíme, že na závorkách, a tedy i pořadí vyhodnocování operací, nezáleží. Můžeme tedy psát jen a1⋄a2⋄...⋄an. Této nezávislosti operace na pořadí vyhodnocování se obecně říká asociativita.
Můžeme tedy úlohu vyřešit přímočaře: vyzkoušíme všechny možnosti, jak vynechat právě jedno číslo, a vybereme si tu, která bude dávat největší NSD. Jedno spočítání NSD n - 1 čísel nás bude stát čas O(n log d), kde d je hodnota největšího čísla, a celkem jich provedeme O(n), tedy celková časová složitost je O(n2 log d).
Intervalové stromy
Jde to ovšem i rychleji, pokud nějak počítání NSD zrychlíme. Pomůže nám právě asociativita: když máme nějaká čísla a1,… ,ak a jejich NSD n1 a čísla b1,… ,bℓ a jejich NSD n2, pak a1⋄… ⋄ak⋄b1⋄… ⋄bℓ= (a1⋄… ⋄ak)⋄(b1⋄… ⋄bℓ) = n1⋄n2. Jinými slovy, dva největší společné dělitele nějakých dvou skupinek čísel umíme v čase O(log d) zkombinovat do jednoho NSD obou skupinek.
Všechny tyto vlastnosti nápadně připomínají to, co potkáme u obyčejného sčítání nebo násobení. Dává tedy smysl, že s operací ⋄ fungují i třeba takové intervalové stromy (o nichž si více můžete přečíst v kuchařce). Nejprve čísla na vstupu v nějakém pořadí uložíme do pole jako a1, …, an. Následně nad polem vytvoříme intervalový strom, který bude fungovat úplně stejně jako součtový nebo minimový intervalový strom, jen bude všude používat operaci ⋄.
S takovým intervalovým stromem umíme jedno škrtnuté číslo vyzkoušet v O(log n log d) času. Zeptáme se totiž intervalového stromu na NSD dvou intervalů: od začátku do škrtnutého prvku a od škrtnutého prvku dále. Každý z obou dotazů pak spočteme v čase O(log n log d), protože počítáme NSD O(log n) hodnot ve vrcholech intervalového stromu a každá hodnota je číslo velké nejvýše O(d). Na vybudování intervalového stromu potřebujeme čas O(n log d), takže celková časová složitost je O(n log n log d).
Optimální řešení
I toho logaritmu se jde zbavit, pokud místo intervalových stromů použijeme nějakou jednodušší strukturu. Inspirujeme se starými dobrými prefixovými součty a vybudujeme si v O(n log d) pole p prefixových NSD, kde p[i] = a1⋄a2⋄a3⋄...⋄ai. To samotné nám ale stačit nebude, protože narozdíl od sčítání neumíme od NSD „odečítat“. Proto si pořídíme ještě pole s suffixových NSD, kde s[i] = ai⋄...⋄an. Snadno se nahlédne, že NSD všech čísel kromě j-tého se spočte jako p[j-1]⋄s[j+1]. Řešení pak běží v čase O(n log d) a paměti O(n).
Poznámky k došlým řešením
- Někteří z vás chybně psali, že čas na spočítání jednoho NSD je O(log n), kde n je počet čísel na vstupu. Je to sice jen drobný prohřešek, ale přesto je dobré dávat pozor na to, které proměnné ve vašem řešení co znamenají.
- Jak se ukázalo, tato úloha sváděla k mnohým nefunkčním heuristikám typu „vezmi několik nejmenších čísel, a jedno z nich buď škrtni, nebo prohlaš za GCD celé řady“. Jakmile vaše řešení obsahuje rozbor mnoha různých případů, často je to znamení, že byste se měli zamyslet, zda pokrýváte všechny případy a zda je řešení každého případu správně. Často také pomáhá zkusit si vymyslet protipříklad, na kterém řešení selže (a třeba zjistit, že žádný protipříklad neexistuje).
 30-5-6 Nápověda na lyžích (Zadání)
30-5-6 Nápověda na lyžích (Zadání)
V úloze jsme měli za úkol najít největší možnou šířku lyžaře – neboli nejužší místo mezi dvěma množinami tyček, kterým musí lyžař projet. Uvědomíme si, že lyžař musí projet napravo od konvexního obalu všech západních tyček (a nalevo od konvexního obalu tyček východních), protože jede po přímce. Kdyby takto vjel dovnitř konvexního obalu, jistě by projel kolem některé tyčky ve špatném směru. Jak konvexní obal sestrojit, si můžete přečíst v naší geometrické kuchařce.
Hledáme tudíž nejkratší úsečku mezi dvěma konvexními mnohoúhelníky. Označíme si je A a B. Uvědomíme si, že takováto úsečka určitě bude mít jeden krajní bod v některém z vrcholů obou mnohoúhelníků. Pokud bychom totiž našli nejkratší úsečku s oběma krajními body na stranách mnohoúhelníků, určitě bychom dovedli najít stejně dlouhou úsečku s jedním krajním bodem ve vrcholu. Příslušná dvojice stran by totiž musela být rovnoběžná (jinak by existovala bližší dvojice bodů), takže by stačilo posunout nejkratší úsečku ve směru kolmém k oběma stranám do nejbližšího vrcholu.
Jednoduché řešení se tedy hned nabízí: v čase O(N2) vyzkoušíme každý vrchol z A zkombinovat se všemi vrcholy a stranami z B a vybereme nejkratší vzdálenost.
Jde to ale lépe. V předchozím řešení pro každý vrchol procházíme celý mnohoúhelník B. To však není nutné: pomůžeme si tím, že si rozmyslíme, kterým směrem se máme k místu (vrcholu nebo hraně druhého mnohoúhelníku) s nejkratší vzdáleností z daného vrcholu vydat. Nejprve si zvolíme počáteční vrchol v A a najdeme z něj nejkratší vzdálenost k B jako v předchozím případě vyzkoušením všech možností. Pokračujeme po hranici A vrcholem sousedícím s počátečním. Nejprve vyzkoušíme tři vzdálenosti: do místa s nejkratší vzdáleností z předchozího vrcholu a do dvou sousedních míst. Vzdálenosti porovnáme a vydáme se po vrcholech a stranách ve směru klesání vzdáleností, dokud vzdálenost opět nezačne růst. Takto postupně pro všechny vrcholy z A najdeme nejbližší místa v B.
Rozmyslíme si, že tento algoritmus opravdu najde nejkratší vzdálenost. Uvažme přímku oddělující oba mnohoúhelníky (z řešení úlohy 30-3-4 víme, že existuje) a celou situaci si představme otočenou tak, aby tato přímka ležela vodorovně. Nyní si z přímky „posvítíme“ na oba mnohoúhelníky, oba se rozdělí na „osvětlenou“ a „tmavou“ část. Nejbližší dvojice bodů určitě leží v osvětlených částech.
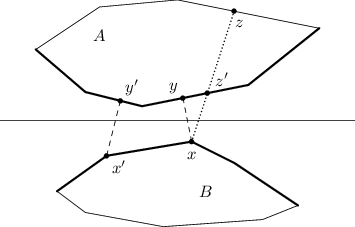
Nyní uvažme libovolný vrchol x∈A. K němu nejbližší místo y∈B leží v osvětlené části B (ke každému tmavému místo z∈B existuje bližší osvětlené místo z'∈B, totiž průsečík polopřímky xz s osvětlenou částí). Vzdálenosti k ostatním osvětleným místům v B směrem od y na obě strany rostou (přesněji neklesají: y může ležet na straně kolmé na úsečku xy; od této strany dál ale už vzdálenost ostře roste). Pokud jsme tedy k předchozímu vrcholu x'∈A znali nejbližší místo y'∈B, stačí se od y' pohybovat po B ve směru klesající vzdálenosti k x, abychom našli správný bod y.
Algoritmus tedy funguje. Jaká je jeho časová složitost? Pokud projdeme osvětlenou část A zleva doprava, projdeme současně osvětlenou část B zleva doprava. Když procházíme tmavou část A, projdeme přitom také právě jednou osvětlenou část B, a to v opačném směru. Každý bod tedy celkem navštívíme O(1)-krát. Jelikož spočítat vzdálenost mezi dvěma body nebo bodem a úsečkou zvládneme v konstantním čase, algoritmus běží v lineárním čase.
Nezapomínejme ovšem, že jsme nejprve museli najít konvexní obaly obou množin bodů. To podle geometrické kuchařky trvá O(N log N), což je také celková složitost našeho řešení.