Třetí série třicátého prvního ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo z každé úlohy série získá alespoň 2 body.
Zadání úloh

Bylo nebylo, za sedmero horami, devatero řekami, dvanáctero městy a dvacatero
nukleonovými urychlovači stálo jedno malé hospodářství, ve kterém bydlel otec
s dcerou. Matka jim nedávno zemřela, a tak se jal otec znovu oženiti. Jeho druhá
žena do domu přivedla také své dvě dcery. Tím však pro ubohou dívku nastaly zlé
časy.
Nevlastní sestry ji nutily tvrdě pracovat, uklízet, vařit, … prostě vše,
co si umanuly. A protože dívenka mívala často tváře umouněné od popela, začaly
jí říkat Popelka. Na rozdíl od Popelky její nevlastní sestry doma nehnuly ani
prstem a zajímaly se jen o drahé šaty a šperky. Chudák otec pak musel každý
druhý týden na nákupy do města.
 31-3-1 Shánění látky (10 bodů)
31-3-1 Shánění látky (10 bodů)
Ve městě se nachází spousta obchodů nabízejících látky. Každý obchod však
prodává jeden metr látky za jinou cenu. Kromě toho cestování také něco stojí,
jelikož se na všech cestách vybírá mýtné. Nevlastní dcery posílají otce na
nákup často, jenomže pokaždé chtějí koupit jiné množství látky. Pravidelné
nákupy jsou poměrně finančně náročné, proto se otec snaží pokaždé naplánovat
trasu tak, aby zaplatil co nejméně peněz. Chudák už je ale z toho všeho
plánování zoufalý.
Město si můžeme představit jako neorientovaný graf, kde vrcholy jsou obchody
a hrany jsou cesty mezi nimi. Každá hrana je ohodnocená
cenou, kterou zaplatíme, když přes ni pojedeme. Každý vrchol je ohodnocen cenou
za jeden metr látky. Jeden z vrcholů je označen jako výchozí, v něm otec
s dcerami bydlí a vždy po nákupu se tam chce vrátit. Navrhněte algoritmus, který
pomůže otci vyřešit jeho problém s plánováním. Algoritmus si nejprve něco
předpočítá a pak bude dostávat dotazy typu „Jak nejlevněji pořídit ℓ
metrů látky?“ Zajímá nás jak doba předvýpočtu, tak časová složitost jednoho
dotazu. Můžete předpokládat, že dotazů bude řádově tolik, co obchodů, a že
v každém obchodě lze koupit libovolné množství látky.
Řešení
Jakmile otec dorazil domů, nevlastní dcery se na nakoupené látky slétly jako
včely na med, začaly si je zkoušet a nakrucovat se před zrcadly. Popelka šla
otce také pozdravit. Všimla si, že má ve vlasech zamotanou lískovou větvičku.
Musela se mu tam dostat cestou z města… Vymotala ji a odnesla do svého
kamrlíku. Sestry by otci nedovolily přivézt Popelce z města žádné cennosti, ale
lískovou větvičku Popelce nechaly. Alespoň má od otce také nějaký dárek.
Jen co se sestry dostatečně nabažily pohledů na látky, vytáhl otec z brašny
ještě jedno překvapení: zlaté náhrdelníky. Ve zdejším království se totiž
chystal veliký ples, na kterém si prý mladý princ měl vybrat jednu dívku,
kterou si vezme za ženu. Otec proto chtěl, aby se dcery mohly dostatečně
vyparádit.
 31-3-2 Cennější náhrdelník (13 bodů)
31-3-2 Cennější náhrdelník (13 bodů)

Obě nevlastní dcery dostaly od otce krásný zlatý náhrdelník.
Protože jsou sestry velmi závistivé, hned se začaly
dohadovat, čí náhrdelník je vzácnější. Hádaly se spolu do té doby, než se jedna
z nich urazila a zavřela se do svého pokoje. Jediný, s kým je ochotna
komunikovat, je jeden ze služebníků.
Sestry chtějí prostřednictvím služebníka zjistit, který náhrdelník je dražší.
Na každém náhrdelníku je sice cenovka, ale protože spolu v současné době
odmítají komunikovat napřímo, chtějí minimalizovat množství informací, které si
spolu vymění. Naštěstí má každá z nich v pokoji
výdobytek moderní doby – generátor náhodných čísel, který funguje tak trochu
magicky. Generuje náhodná čísla tak, že i-té náhodné číslo první
sestry je shodné s i-tým náhodným číslem druhé sestry. Vymyslete způsob,
jakým sestry s pravděpodobností alespoň 75 % dokáží zjistit, čí
náhrdelník je dražší.
Jak je v kryptografii běžným zvykem, pojmenujeme si sestry Alice a Bob. Každá
má jedno binární číslo délky N a zázračný generátor, který jim oběma generuje
stejná náhodná čísla. Cílem je s pravděpodobností alespoň 75 %
zjistit, která ze sester má větší číslo, a to na co nejmenší počet vyměněných
bitů. Algoritmus musí pro každý vstup odpovědět správně s pravděpodobností
75 %, tedy nestačí vymyslet algoritmus, který odpoví správně na
75 % vstupů.
 Lehčí varianta (za 8 bodů): Zjistěte jen, zda jsou oba náhrdelníky stejně drahé.
Lehčí varianta (za 8 bodů): Zjistěte jen, zda jsou oba náhrdelníky stejně drahé.
Řešení
Několik týdnů se sestry připravovaly na ples, nechaly si ušít z látek nádherné
šaty a učesat ohromující účesy. Všichni se na ples moc těšili. Když konečně
nastal den D a sestry se nachystaly k odchodu, velmi je překvapilo, že Popelka
chce jít taky. Vždyť tu má ještě spoustu práce! Popelka však tvrdila, že má vše
hotové. Poslední týden tvrdě pracovala, aby měla nyní volno. To sestry
naštvalo. Vzaly popel a hrách a sesypaly ho na zem.
Popelka byla celá zoufalá. „Vždyť tohle nemůžu v nějakém konečném čase
stihnout roztřídit!“ „Ťuk, ťúúúk, ťúúúk, ťuk“ ozvalo se najednou. To na okno
ťukal malý holoubek. Popelka, která byla zběhlá v luštění morseovky, pochopila,
že se jí holoubek snaží nabídnout pomoc.
 31-3-3 Přebírání hrachu (9 bodů)
31-3-3 Přebírání hrachu (9 bodů)
Na podlaze se nachází sesypaný hrách s popelem a mezi tím poskakuje několik
holoubků a vrabčáků. Chtějí Popelce pomoct vysbírat všechen hrách. Pro každou
kuličku hrachu chceme zjistit, zda ji nějaký ptáček dokáže sezobnout a přenést
do ošatky. Holoubci i vrabčáci se však pohybují každý jinak. Vrabčáci poskakují
rovně dopředu, dozadu, doleva i doprava, zato holoubci chodí šikmo do všech
čtyř stran.
Celou situaci si lze představit jako rozmístění figurek na šachovnici.
Holoubci představují černé střelce, vrabčáci černé věže a kuličky hrachu pak
bílé pěšáky. Pro každou bílou figurku chceme zjistit, zda ji dokážeme v jednom
tahu nějakou černou figurkou vyhodit.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku vstupu se nachází dvě čísla B a C, a to
počet kuliček hrachu (neboli bílých figurek) a počet ptáčků (neboli černých
figurek). Na dalších B řádcích se nachází souřadnice kuliček hrachu jako
dvojice čísel oddělených mezerou, číslo řádku a číslo sloupce udávajících, kde
se kulička nachází. Na dalších C řádcích se pak nachází pozice ptáčků – každý
takový řádek obsahuje znak H nebo V a dvojici čísel udávajících
řádek a sloupec, kde ptáček stojí (opět vše oddělené mezerami). Znak H
značí holoubka (pohybuje se jako střelec) a znak V vrabčáka (pohybuje se
jako věž). Figurky na vstupu mohou být seřazené náhodně.
Formát výstupu: Na B řádků výstupu vypište (ve stejném pořadí, jako na
vstupu) pro každou kuličku hrachu ANO nebo NE podle toho, jestli
existuje nějaký holoubek nebo vrabčák, který může tuto kuličku hrachu jedním
tahem sezobnout.
Ukázkový vstup:
4 3
0 1
0 2
0 3
2 2
V 0 0
H 1 3
V 3 3
Ukázkový výstup:
ANO
ANO
NE
ANO

Poznámka: Všimněte si, že stejnou černou figurkou (střelcem) můžeme vzít
dva bílé pěšce. Naopak bílého pěšce vpravo nahoře nemůžeme vzít ani spodní věží
(v cestě stojí střelec), ani levou věží (v cestě stojí jiné bílé figurky).
Řešení

Sestry netušily, že si Popelka rozumí s ptáčky, a měla tak vše za chviličku
hotové. Ples by ještě stihla, ale kde teď narychlo sehnat šaty? Rozesmutnila se
a rozběhla se do svého kamrlíku, kde se rozplakala. Proč jen má takové
závistivé sestry, které jí nedovolí ani podívat se na ples! Rozhodla se, že si
spraví náladu jídlem, a vzpomněla si na lískový oříšek od otce. „Ten bude
určitě velice chutný,“ pomyslela si. Když ho však rozlouskla, nemohla uvěřit
svým očím. Zevnitř vykukoval cíp šatů! Popelka zatáhla a z oříšku vypadly tak
nádherné šaty, jaké ještě nikdy neviděla.
Když Popelka dorazila na ples, všichni byli okouzleni její krásou. Nevlastní
sestry ji nepoznaly, protože doma nenosila nic jiného než otrhané šaty umazané
od popela. Popelky si všiml dokonce i samotný princ a začal se prodírat davem
tanečníků, jen aby si s ní mohl zatančit.
 31-3-4 Dláždění sálu (11 bodů)
31-3-4 Dláždění sálu (11 bodů)
Ples se odehrává v největším a nejhonosnějším sálu na zámku, který nedávno
prošel rekonstrukcí. Podlaha je nyní vydlážděná krásně barevnými dlaždicemi.
Občas spolu ale sousední dlaždice neladí. Uměli byste sál vydláždit lépe?
Sál má obdélníkový půdorys o rozměrech K × N metrů a každá z jeho čtyř
stěn je obarvená jednou barvou. Naším úkolem je sál vydláždit barevnými
dlaždicemi o rozměrech 1 × 1 metr. K tomu jich máme dispozici hned
několik druhů, přičemž každý druh dlaždice má pevně určené obarvení hran.
Z estetických důvodů také s dlaždicemi nemůžeme otáčet, tj. každý druh dlaždice
má určeno, která hrana bude otočená na sever. Od každého druhu můžeme použít
neomezeně dlaždic. Umíme sál vydláždit, aby přiléhající hrany sousedních
dlaždic a hrany sousedící se stěnami sálu barevně ladily? Zajímá nás časová
a paměťová složitost pouze vzhledem k N, můžete předpokládat, že hodnota K
a seznam povolených druhů dlaždic jsou pevně dané.
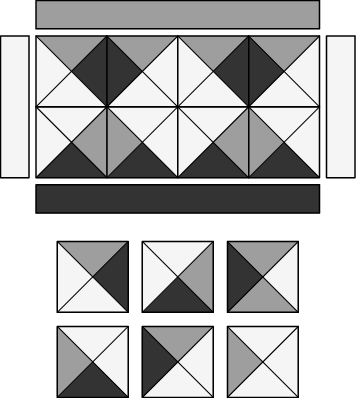
V příkladu máme k dispozici šest druhů dlaždic, z nichž čtyři se od sebe liší
jenom otočením (my však dlaždicemi otáčet nemůžeme, takže je považujeme za
různé). Znázorněn je sál s K = 2 a N = 4 a jeho (jediné) vydláždění.
Rozmyslete si, že pro K = 2, tyto druhy dlaždic a obarvení stěn umíme vydláždit
právě všechny sály se sudou šířkou.
Řešení
Komentáře
Když už se blížila půlnoc, Popelka si uvědomila, že se musí dostat domů dříve
než její sestry, aby nikdo nepoznal, že na plese byla taky. Omluvila se tedy
princi a zamířila ke schodům vedoucím ven z paláce. Princ se však během plesu
stihl do Popelky zamilovat, a tak nezaváhal ani vteřinu a okamžitě se za ní
rozběhl. „Neodcházej! Vždyť já ani neznám tvé jméno!“ zavolal za Popelkou.
Jak se Popelka na schodech za princem ohlédla, ztratila na chvilku rovnováhu
a nedopatřením se jí vyzul jeden střevíček. Princ jí však byl natolik v patách,
že nechala střevíček střevíčkem a vyběhla ven z paláce.
Princ byl tuze smutný, že mu právě prchla největší láska jeho života. Jediné,
co mu po ní zůstalo, byl onen střevíček. Rozhodl se, že pomocí něj neznámou
princeznu vypátrá.
 31-3-5 Hledání princezny (11 bodů)
31-3-5 Hledání princezny (11 bodů)
Princ chce zjistit, komu střevíček padne. Jeho království je ale opravdu
rozlehlé, a tak není v jeho silách zajít za každým osobně. Naštěstí však
království o každém poddaném eviduje spoustu informací, včetně adresy bydliště
a velikosti nohy (čirou náhodou je celý soupis seřazený zrovna podle velikosti
nohy). Navíc je dvorní švec schopen podle předlohy vyrobit střevíček na chlup
stejný jako originál. Výroba jednoho takového střevíčku trvá přibližně jednu
hodinu.
Princ dostal nápad: Nechal po celém království vyhlásit, že každou hodinu pošle
jednomu z poddaných střevíček, aby si ho vyzkoušel a v odpovědi poslal, zda mu
je malý, velký, nebo akorát. Princ, znalý binárního vyhledávání, počítal s tím,
že tak svou lásku dokáže najít v čase logaritmickém k počtu poddaných. To se
ale přepočítal! Královská pošta už má svá nejlepší léta za sebou, a tak poslání
střevíčku poddanému a následné doručení odpovědi trvá K hodin, kde K může
(ale nemusí) být závislé na počtu poddaných v království. Jak má princ
postupovat?
Trošku formálněji řečeno: Máme setříděné pole N čísel, ve kterém chceme najít
konkrétní hodnotu. Dotaz můžeme poslat jednou za hodinu, ale trvá K hodin,
než nám zpátky přijde odpověď. Dotazů můžeme mít na cestě více. Najděte časově
efektivní algoritmus v závislosti na K.
Řešení
Pátrání trvalo už několik týdnů a princ už začínal být celý zoufalý, že svou
lásku nikdy nenajde. Až byl jednoho dne poslán střevíček také Popelce.
Nevlastní sestry si byly jisté, že Popelce střevíček patřit nemůže, a tak jí ho
ani nechtěly dát vyzkoušet. Otec se však (poprvé za celý svůj život) postavil
proti jejich vůli a střevíček Popelce přinesl.
Jak byli všichni překvapeni, když Popelce střevíček padl jak ulitý. Princ
nechal pro Popelku okamžitě poslat kočár a odvezl si ji k sobě na zámek. Za
necelý týden se pak konala velkolepá svatba.
A žili spolu šťastně až do smrti…
Zuzka Urbanová & Klárka Tauchmanová
 31-3-6 Model–ViewController (15 bodů)
31-3-6 Model–ViewController (15 bodů)
Třetí díl seriálu pokračuje vyráběním simulátoru dopravy na křižovatce.
Minule jsme si slíbili, že v programech konečně uklidíme a začneme
programovat čistě, tak si to pojďme splnit.
Prvně je však třeba učinit důležité oznámení. Vývojáři Qt5 převzali projekt
PySide, což je, stejně jako PyQt, rozhraní knihovny Qt pro Python. Vytvořili
PySide2 jako oficiální rozhraní Qt5 pro Python. My tedy taktéž opustíme PyQt5
a budeme pokračovat s PySide2. Práce s ním je, alespoň pro naše účely,
stejná jako s PyQt5. V našich programech by se nemělo téměř nic změnit, kromě toho,
že nebudeme psát from PyQt5 ..., ale from PySide2 ...; to je
jednoduché, ne?
Přece jenom se ale něco změnilo:
- Data přečtená ze socketu je třeba regulérně dekódovat skrze knihovnu Qt;
už nedostáváme pythoní
bytearray, nýbrž QByteArray, který dekódujeme
pomocí objektu QTextCodec.
- Metody předávané jako cíl událostí je vhodné označit dekorátorem
@Slot(...),
ale není to nutné.
- Pro spuštění programu nelze volat
exec(), je nutné použít exec_().
Od nynějška také čerpáme z dokumentace přímo pro PySide2 na webu Qt; stále je však třeba pro podrobnější popis
a detaily jednotlivých metod sáhnout do dokumentace pro C++.
Debian Buster již PySide2 obsahuje; pokud nemáte balíčky pro svůj systém,
použijte Pip, stejně jako v prvním díle. Pokud nevíte, co je Pip nebo jak
jej požít, napsali jsme návod na Pip.
$ pip3 install pyside2
Návrhový vzor Model–View–Controller (MVC)
Základem programu je datový model. V případě našeho simulátoru dopravy na
křižovatce to jsou informace o poloze aut. Do modelu patří i časovače,
které posílají auta pryč.
Uživatel by s datovým modelem neměl přijít do styku. Data jsou uložena
ve strojově čitelné formě a přistupuje se k nim pomocí hezkého a milého API.
Aby však uživatel nepřišel zkrátka, je tady náhled, čili View.
To je ta část GUI, která uživateli oznamuje nějaké informace;
například vypisovátko jednotlivých aut a chodců ve sledovaném úseku.
Model informuje View o změnách zobrazovaných dat, například pokud přijede
další auto. Nebo si View naopak pravidelně říká Modelu o data.
Na opačné straně je Controller, čili ovladač. Uživatel
prostřednictvím Controlleru ovládá Model. Controller tedy překládá například
stisk tlačítka na volání nějakého vnitřního API. Controller také ovládá přímo
View, pokud není třeba volat Model.
 Hezky napsaný program pak dokáže mít několik různých rozhraní, mezi kterými
je možno si vybrat; například jedno v Qt, jedno jako webovou aplikaci, jedno
v terminálu v Curses a jedno čisté API pro skriptování. To je takový svatý
grál programování s uživatelským rozhraním, ne povinnost. Je však dobré
pamatovat na to, že má být program takto rozdělitelný, už při prvotním rozmýšlení.
Ušetříte si tak spoustu práce.
Hezky napsaný program pak dokáže mít několik různých rozhraní, mezi kterými
je možno si vybrat; například jedno v Qt, jedno jako webovou aplikaci, jedno
v terminálu v Curses a jedno čisté API pro skriptování. To je takový svatý
grál programování s uživatelským rozhraním, ne povinnost. Je však dobré
pamatovat na to, že má být program takto rozdělitelný, už při prvotním rozmýšlení.
Ušetříte si tak spoustu práce.
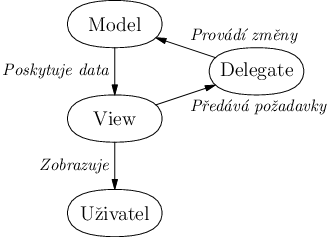
Qt nicméně počítá s tím, že View a Controller jsou propojené do jednoho modulu,
proto se tomuto modelu v Qt říká pouze Model–View. O změny dat se pak stará Delegate,
což je vlastně ta část Controlleru, která komunikuje s Modelem; o komunikaci s uživatelem se stará View.
Simulátor dopravy: Model
Datový model je v našem simulátoru seznam aut a chodců, které máme aktuálně v oblasti.
Model zdědíme z třídy QAbstractListModel, která do sebe balí seznam
– to přesně potřebujeme. V ní potřebujeme nadefinovat dvě metody, které volá
view, když si chce přečíst data:
rowCount vrací počet řádků v seznamu (jako číslo)- a
data vrací samotná data uložená v modelu.
Qt počítá s tím, že seznam může být dvourozměrný; na tento model se tak může napojit
například QTableView, který zobrazuje tabulku. My použijeme QListView, viz níže.
Metoda data tedy jako první argument dostane objekt typu
QModelIndex, ze kterého získáme číslo řádku zavoláním metody row.
Jako druhý argument pak dostaneme číselnou hodnotu role (Qt.ItemDataRole); v Qt jsou definovány konstanty jako
Qt.DisplayRole, Qt.DecorationRole nebo například Qt.ToolTipRole,
které určují, v jakém kontextu si View žádá data. My pro začátek použijeme pouze DisplayRole,
pro kterou se vrací řetězec (str) pro daný řádek.
Metoda tedy ověří, jestli je index v povoleném rozsahu, jestli je správná role, a vrátí příslušnou
reprezentaci cestovatele. Pro DisplayRole je to textová reprezentace.
Data v modelu je třeba upravovat přidáváním a ubíráním řádků podle toho, jak přibývají a ubývají
cestovatelé. Na to si napíšeme vlastní metody add a remove. Ještě
je třeba šťouchnout do View; proto příslušné části kódu obalíme voláním
beginInsertRows a endInsertRows,
resp. beginRemoveRows a endRemoveRows. Zbytek zařídí model za nás.
K modelu připojíme síťové rozhraní CrossingNetwork, které nyní nedělá nic
jiného než most mezi modelem a síťovým socketem.
Nakonec si pořídíme QListView. Tomu stačí připojit model a máme prakticky
hotovo.
Jednoduchá implementace simulátoru s využitím techniky Model–View
Úkol 1 [3b]
Přidejte cestovatelům ikonky. Ikonku načtete zavoláním QIcon(soubor),
přičemž třídu QIcon importujete z balíku PySide2.QtGui. Pokuste se
uložit ikonu na co nejrozumnější místo tak, aby se načetla právě jednou. Ikonu
vracejte z metody data pro roli Qt.DecorationRole.
Pokud se vám ikonky nechce hledat jinde nebo vyrábět vlastní, můžete si
stáhnout amatérské (ikonku
auta a
chodce) od nás.
Úkol 2 [5b]
Upravte simulátor tak, aby se místo ID a rychlosti zobrazovala aktuální poloha
cestovatele ve sledovaném úseku (absolutní v metrech a relativní v procentech).
ID a rychlost nechť se zobrazují v tooltipu (Qt.ToolTipRole).
Ke spočítání polohy můžete využít metodu position třídy Traveller.
Polohu v zobrazení nemusíte nikterak aktualizovat, co s tím, si ukážeme za chvíli.
Vzhledem k nepřesnosti časovačů se může stát, že se bude ze začátku zobrazovat
záporná poloha; to řešit nemusíte.
Proxy Model
Mezi samotným datovým modelem a View potřebujeme často ještě nějaké vrstvy, které
data nějak transformují. Je tak možné například data třídit nebo s nimi dělat
ledasjaké jiné psí kusy.
Takovým vrstvám se říká Proxy modely a jsou to třídy, které mají navenek téměř
stejné rozhraní jako běžný model, ale ve skutečnosti nenesou žádná data. Místo toho
jsou připojené na jiné modely, které jim data poskytují.
Úplně základní proxy je QIdentityProxyModel, který jenom propouští data oběma směry.
Pro demonstraci uděláme úplně neužitečnou změnu metody data:
class DisplayProxy(QIdentityProxyModel):
def data(self, index, role):
model = self.sourceModel()
original = model.data(index, role)
if role == Qt.DisplayRole:
return "proxy! " + original
else:
return original
V konstruktoru třídy Crossing pak zapojíme proxy do procesu takto:
self.model = CrossingModel()
self.displayProxy = DisplayProxy()
self.displayProxy.setSourceModel(self.model)
# ...
self.listView.setModel(self.displayProxy)
Odchytávat signály (které vydává model) je podstatně těžší, to si necháme na jindy.
Vydávat je ale můžeme; speciálně se nám bude hodit signál dataChanged,
který se vydává pokaždé, když se nějaká hodnota změní. Ten můžeme vydat i ručně.
# ... došlo ke změně dat
# První změněný index
f = model.createIndex(prvni, 0)
# Poslední změněný index
t = model.createIndex(posledni, 0)
# Odeslat zprávu
model.dataChanged.emit(f, t)
Argumenty signálu dataChanged je rozsah (od–do včetně) indexů, na kterých došlo ke změně.
A protože model nemusí být jenom seznam, ale ledacos úplně obecného, tak se předávají objekty
typu QModelIndex. View si tento signál zaregistruje a obvykle na něj zareaguje novým
načtením příslušných dat, je-li to potřeba.
Úkol 3 [4b]
Napište model proxy, která bude pravidelně aktualizovat data (volat dataChanged)
každých 500 milisekund.
Kromě obyčejného proxy modelu nám Qt dává k dispozici QSortFilterProxyModel. Tento proxy model,
jak název napovídá, dokáže data třídit a filtrovat. Jak zapojit model proxy
mezi model a view, to už víme, jen se hodí doplnit, že proxy samozřejmě můžeme řetězit za sebe.
Kdybychom místo QListView použili QTableView, pak by nebylo třeba učinit nic dalšího,
než zavolat na tento view metodu setSortingEnabled, která umožní
uživateli volit směr řazení. My však místo toho zavoláme na model metodu sort:
model.sort(0, Qt.AscendingOrder)
Toto volání bude třídit podle sloupce 0 (jiný totiž nemáme) ve vzestupném pořadí. Jenže standardně
se třídí podle DisplayRole; to se dá změnit zavoláním setSortRole. Roli si můžete
nadefinovat vlastní; nejmenší bezpečná je Qt.UserRole. Na začátku programu tedy napíšeme
třeba mySortRole = Qt.UserRole, při inicializaci modelu zavoláme model.setSortRole(mySortRole)
a v metodě data našeho zdrojového modelu vrátíme pro tuto roli data, podle kterých se bude třídit.
Stejným způsobem se dá i filtrovat data, například zobrazit jen auta nebo
chodce; tím se více zabývat nebudeme, zájemce odkazuji na webovou dokumentaci.
Úkol 4 [3b]
Použijte QSortFilterProxyModel k zobrazování seznamu cestovatelů
setříděného podle toho, jak daleko od začátku své trasy jsou. Případné
chvilkové nepřesnosti ve třídění můžete ignorovat.
Tím je třetí díl seriálu u konce. Omlouváme se za pozdní vydání a zkusíme to
příště stihnout rychleji. A co bude příště? Zkusíme napsat vlastní View
a vykreslit nadchod, chodce a auta v jednoduché grafice. A pokud se podaří, tak
postavíme přechod a ukážeme, jak se píše Controller, resp. Delegate.
Maria Matějka
Řešení

 31-3-1 Shánění látky (10 bodů)
31-3-1 Shánění látky (10 bodů)
 Lehčí varianta (za 8 bodů): Zjistěte jen, zda jsou oba náhrdelníky stejně drahé.
Lehčí varianta (za 8 bodů): Zjistěte jen, zda jsou oba náhrdelníky stejně drahé. 31-3-3 Přebírání hrachu (9 bodů)
31-3-3 Přebírání hrachu (9 bodů)


 31-3-6 Model–ViewController (15 bodů)
31-3-6 Model–ViewController (15 bodů)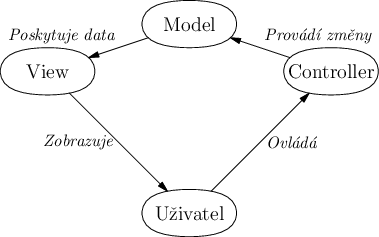
 Hezky napsaný program pak dokáže mít několik různých rozhraní, mezi kterými
je možno si vybrat; například jedno v Qt, jedno jako webovou aplikaci, jedno
v terminálu v Curses a jedno čisté API pro skriptování. To je takový svatý
grál programování s uživatelským rozhraním, ne povinnost. Je však dobré
pamatovat na to, že má být program takto rozdělitelný, už při prvotním rozmýšlení.
Ušetříte si tak spoustu práce.
Hezky napsaný program pak dokáže mít několik různých rozhraní, mezi kterými
je možno si vybrat; například jedno v Qt, jedno jako webovou aplikaci, jedno
v terminálu v Curses a jedno čisté API pro skriptování. To je takový svatý
grál programování s uživatelským rozhraním, ne povinnost. Je však dobré
pamatovat na to, že má být program takto rozdělitelný, už při prvotním rozmýšlení.
Ušetříte si tak spoustu práce.