Pátá série osmého ročníku KSP
Řešení úloh
- 8-5-1: Rozmarný princ
- 8-5-2: Telefon do pekla
- 8-5-3: Pomsta šíleného zahradníka
- 8-5-4: Čekej, Snad Dojede
- 8-5-5: Automata finita
8-5-1 Rozmarný princ (Zadání)
Tuto úlohu vás moc neřešilo a z těch, kteří ji řešili, ji zpracoval dobře pouze Dan Kráľ. Úkolem bylo najít dobrou strategii, díky níž by princezna pokud možno vždy vyhrála. Většina z vás psala pouze programy, které by sice princezně pomohly, ale pouze v jistých situacích, a ke všemu jste neuvedli důkazy svých tvrzení, takže jste si ani nemohli být správností jisti. Je pravda, že pokud je na počátku na všech hromádkách stejné množství sirek a začíná princ a počet hromádek je sudý, tak stačí opakovat tahy po princi, ale na jiné hromádce, a tento postup vede jistě k vítězství, leč toto vítězství má velké předpoklady a pravděpodobnost splnění těchto předpokladů je malá.
Definice: Nechť M je maximální počet najednou odebratelných sirek z jedné hromádky, N je počet hromádek, hi je i-tá hromádka, i=1,2,… ,N, pi je počet sirek na hi. Strom hry je struktura složená z uzlů a hran. Uzly odpovídají herním pozicím, každý uzel nese úplnou informaci o všech hromádkách. Kořen stromu odpovídá výchozí pozici. Z každého uzlu vede tolik hran, kolik je z dané pozice možných regulérních tahů. Algoritmus generuje sekvence půltahů z dané pozice, dokud není dosaženo pozice, která je pro hráče na tahu vyhraná. Pokud projde všechny možnosti a nenajde pozici, která je pro hráče vyhraná, odebere jednu sirku z největší hromádky. Půltahem je myšleno odebírání sirek jednoho hráče, tj. např.princezny. Vyhraná pozice je taková, že ať z této pozice protihráč odebírá jakkoliv, potom hráč používající algoritmus uvedený níže určitě vyhraje.
Algoritmus: Vyberu jen ty hromádky, pro něž platí pi mod (M+1) ≥ 1. Nanaleznu-li žádnou takovou, neexistuje z aktuální pozice sekvence půltahů vedoucí k výhře a skončím. Pro všechny vybrané hromádky provedu: Je-li pi > 1+M, pak pi := pi mod (M+1). Pro takto vzniklé hromádky provedu: Zkusím odebrat z libovolne hromádky nějaký přípustný počet sirek, pokud nelze udělat žádné přípustné odebrání, aniž bych prohrál, skončím s výsledkem false, jinak pokračuji.
Pro daný výběr rekurzivně zavolám algoritmus od prvního kroku (generuji půltah soupeře). Pokud se z rekurze vrátím s výsledkem true, provedu jiný výběr sirek (jiný počet a z jiné hromádky tak, abych postupně prošel všechny možnosti). Pokud se vrátím s výsledkem false, zapamatuji si hromádku H1, ze které jsem vybíral, a počet sirek, který jsem z ní odebral. Našel jsem půltah vedoucí k vítězství a skončím s výsledkem true. Pokud vždy dostanu true, neexistuje v tuto chvíli půltah vedoucí k vítězství, a tak skončím s hodnotou false.
Pokud tento postup skončí s výsledkem true, existuje vyhrávající posloupnost. Ze vstupní množiny hromádek odeberu ze zapamatované hromádky (H1) zapamatovaný počet sirek. Pak nechám hrát soupeře a zapamatuji si, ze které hromádky odebíral a kolik odebral (P). Pokud odebral z hromádky, na níž je ještě více než 1+M sirek, pak z ní odeberu M+1-P sirek. Pokud ne, postupuju od kroku 1.
Tvrzení: Pokud bude jednou výsledkem výše uvedeného algoritmu, podle něhož hraje počítač, hodnota true, pak hráč, jenž je právě na tahu, používající tento postup, vyhraje.
Důkaz: (nejprve pro jednu hromádku)
Tvrzení:
- Jsem-li na tahu a je-li na hromádce některý z tohoto počtu sirek: 2… M+1 (je to vyhraná pozice), pak mohu odebrat tak, aby na hromádce zbyla jen jedna, a tudíž soupeř prohraje.
- Přidám-li k vyhrané pozici (např. s P sirkami ) M+1 sirek, pozice zůstane stále vyhraná, neboť odebere-li soupeř z hromádky P sirek , mohu odebrat M+1-P sirek, abych se dostal do původní vyhrané pozice. Důsledek: Je-li na hromádce K·(M+1) +1 sirek (K je přirozené či nula), je tato hra pro hráče na tahu prohraná.
- Je-li na hromádce P sirek a P mod (M+1)=1, pak z této
pozice nelze vyhrát – je to důsledek T1 z pohledu protihráče.
Mějme nyní více hromádek…Definujme hru H1 tak, že vypustíme z hry hromádky, na nichž je tolik sirek, že platí P mod (M+1)=1 (podmínka P1), kde P je počet sirek na dané hromádce.
- Jsem-li na tahu, stačí hledat sekvenci půltahů pouze ve hře H1. Naleznu-li v H1 sekvenci půltahů vedoucí k vítězství a pokud soupeř odebere z některé z hromádek, které nejsou v H1 (např. hromádka Hi) , pak lze dle T2 z téže hromádky odebrat sirky tak, aby podmínka P1 stále platila, a tudíž se opět dostaneme do vyhrávající pozice.
- Jsem-li na tahu a algoritmus skončí s výsledkem true, pak nenašel pro pozici soupeře žádnou sekvenci půltahů vedoucí k jeho vítězství. Pak ať odebere soupeř cokoliv, prohraje. Provede-li soupeř tah, potom lze opakováním algoritmu, tj. průchodem stromu pozic, opět nalézt vyhrávající pozici, neboť algoritmus předtím prozkoumal všechny soupeřovy půltahy. Pokud algoritmus skončí s výsledkem false, pak odebere 1 sirku z největší hromádky.
Celý algoritmus je obdoba minimaxu a jeho důkaz je uveden v mnoha knihách, proto je zbytečné rozepisovat jeho důkaz do podrobností. Tento univerzální způsob se používá i v jiných hrách, jako jsou třeba šachy, dáma, piškvorky, … Složitost algoritmu je však značná díky rekurzivnímu prohledávání. Velkou roli hraje konstanta M, díky níž se nemusí prohledávat všechny možnosti, ale pouze hromádky do velikosti M+1. Složitost v tomto rozmezí je však nepolynomiální vzhledem k počtu sirek a hromádek.
Popis procedur a funkcí:
Throm … reprezentace hromádek.
hrajP(sez:Throm) … rekursivní funkce, která hraje při liché
hloubce volání jako princ (protihráč), při sudé jako princezna.
hrajPoc(sez:Throm; var sez1:Throm) … hra princezny a počítače.
Funkce vrací true, pokud nenastal konec hry.
hraj … hraje střídavě princezna a princ.
8-5-2 Telefon do pekla (Zadání)
Tento pekelný spojařský problém je možno vyřešit velice efektivně za pomoci metody "Rozděl a panuj", tedy rozdělením úlohy na dvě menší části, s nimiž se později vypořádáme analogicky. Většina z vás si tento postup zvolila a více či méně elegantně tak dosáhla časové složitosti O(N· log N), stejně jako u následujícího algoritmu:
Mějme "levé konce" označené l1, …, ln a "pravé konce" r1, …, rm, o nichž víme, že jsou navzájem propojeny s výjimkou případů, kdy drát nevede (musíme počítat s tím, že n nemusí být rovno m – to nastane u kabelů s nevodivými dráty). Nyní rozdělíme levé konce na dvě pokud možno stejně velké části – řekněme l1, …, lk a lk+1, …, ln a k jedné (řekněme první) časti připojíme napětí, zatímco od druhé jej odpojíme. Poté změříme napětí na pravých koncích – ty, na kterých něco naměříme, jsou jistě připojeny pouze k levým koncům z první části (tedy k těm, na něž jsme napětí připojili), zatímco ty zbylé jsou buďto připojeny k levým koncům z části druhé nebo nepřipojeny. Takto jsme rozdělili dráty na dvě (přibližně stejně velké) části, které můžeme zpracovávat stejným způsobem.
Některé případy jsou ovšem natolik triviální, že si zasluhují zvláštní pozornost:
- n=0 ∧ m>0: k pravým koncům není evidentně nic připojeno (kdyby bylo, jistě by se to dle předpokladů nacházelo mezi zkoumanými levými konci, které ovšem žádné nemáme).
- n=1 ∧ m=1: pokud byl na r1 alespoň jednou naměřen proud, jistě je l1 propojen s r1. Pokud nikoliv, je to třeba vyzkoušet, neboť je zde ještě možnost, že by byl drát přerušen.
- n>0 ∧ m=0: k levým koncům není evidentně nic připojeno.
Ukázkový program pracuje přesně podle tohoto algoritmu – funkce test
zabezpečuje otestování nějakých k sobě patřících levých a pravých konců,
přičemž její argumenty udávají první a poslední číslo zkoumaných levých
konců (jistě můžeme postupovat tak, abychom zkoumali vždy souvislý úsek),
zatímco pravá čísla konců k těmto patřící jsou uložena v poli r
a je předán pouze počátek a konec úseku v tomto poli. Dále je funkci
dodána informace o tom, zda je úsek zrovna zapnut nebo vypnut, a protékal-li
úsekem již alespoň jednou proud.
Funkce test po ošetření triviálních případů úsek rozdělí volbou
k=⌊n/2 ⌋ a buďto připojí napětí k první polovině (v případě,
že úsek nebyl pod napětím) nebo jej od druhé poloviny odpojí (byl-li
již pod napětím), čímž se minimálním počtem přepnutí dostaneme do kýženého
testovacího stavu. Dále testujeme stav jednotlivých pravých konců a prohazujeme
jejich čísla v poli r tak, aby na konci r1 až rl byly ty konce,
na nichž jsme napětí naměřili, a rl+1 až rm ty zbylé. Poté voláme
funkci test rekurzivně. Hloubka rekurze může být nejvýše O(log N),
v každé úrovni provádíme O(N) operací, takže celková časová složitost
je přesně dle očekávání.
Pro interakci s příslušným služebným čertem obsluhujícím tester jsou
použity funkce On, Off a Measure snad dostatečně výmluvných názvů.
8-5-3 Pomsta šíleného zahradníka (Zadání)
Tento příklad řešilo jen několik z vás, a přesto s jeho opravováním bylo práce dost a dost. Stále ještě jste si nezvykli doprovodit svá řešení zdůvodněním použitého postupu, a tak bylo často potřeba dívat se hluboko do programu, abych zjistil, jak vlastně chcete isomorfismus stromů určit.
Ve vzorovém řešení použijeme následující myšlenku: jsou-li isomorfní stromy a a b a dále jsou isomorfní b a c, pak jsou i a a c isomorfní (tranzitivita isomorfismu). Pokud tedy umíme pro každý strom najít jakýsi standardní strom k němu isomorfní, pak stačí zjistit, zda jsou tyto normalizované stromy stejné. Tranzitivitu dokážeme indukcí podle počtu listů:
- Pro a=b=c=∅ není o čem mluvit.
- Nechť tvrzení platí pro stromy s nejvýše n listy, nechť a, b, c mají n+1 listů (isomorfní stromy zřejmě mají stejně listů). Nechť a=(a1,a2), b=(b1,b2), c=(c1,c2), nechť BÚNO (Bez Újmy Na Obecnosti – další případy obdobně) a1=b1, b1=c1 a a2=b2, b2=c2. Pak podle předpokladu a1=c1 a a2=c2, a tedy podle definice a=c.
Nyní tedy stačí najít rychlý algoritmus, jenž ke každému stromu najde jeho normalizaci.
Normalizovaný strom bude strom, pro který platí, že je to buď ∅, nebo je to strom (a,b), kde a≥ b a a a b jsou normalizované stromy. Přitom relace ≥ je libovolné lineární uspořádání normalizovaných stromů (tedy takové, že pro pro každé normalizované stromy a a b platí právě jedna z možností a<b, a>b, a=b). Pro náš případ bude stačit třeba porovnání řetězcových zápisů stromů (pro normalizované stromy je jednoznačné a jak se ukáže, bude dostatečně rychlé).
Paměťová složitost tak zůstává lineární k délce zápisu stromu (označme ji N). Jaká je časová složitost? Při průchodech porovnáváme každý uzel maximálně N-krát, stejně tak jej maximálně N-krát přesuneme. Přitom průměrný počet přístupu k uzlu bude log N. Uzlů je O(N), proto časová složitost je průměrně O(N · log N), maximálně O(N2). Uvědomme si, že závěrečné porovnání stromů je lineární.
Vzorový program vychází z řešení D. Kráľe.
8-5-4 Čekej, Snad Dojede (Zadání)
Analogie železniční sítě s grafem, ve kterém stanicím odpovídají vrcholy a jízdám vlaku mezi stanicemi hrany, je nabíledni. Následující řešení je založené na mírně modifikovaném Dijkstrově algoritmu.
Popis algoritmu:
Ohodnocení každého vrcholu určuje čas, ve kterém se umíme do tohoto vrcholu dostat. Ohodnocení může být buď trvalé nebo dočasné.
Na začátku dočasně ohodnotíme vrchol, ze kterého vyjíždíme, časem, ve kterém v něm jsme. Ostatní vrcholy jsou zatím bez ohodnocení, resp. ohodnoceny na dočasné nekonečno. Dále vždy vybereme z dočasně ohodnocených vrholů ten s sejmenším ohodnocením (v prvním kroku to bude ten, ze kterého vyjíždíme), ohodnotíme ho tou samou hodnotou trvale, a u všech vrcholů, do kterých se můžeme přímo dostat z tohoto vrcholu, zkontrolujeme, zda se tam nemůžeme dostat dříve – v tomto případě dočasné ohodnocení patřičně upravíme.
Jakmile trvale ohodnotíme vrchol, do kterého se máme dostat, končíme, a zrekonstruujeme cestu, po které jsme se do něj dostali.
Bližší popis Dijkstrova algoritmu je možné najít téměř v každé knize, která se zabývá algoritmy (např. v [1]). To, co činí tuto úlohu zajímavou, jsou datové struktury:
Jména stanic nám na vstup přicházejí jako řetězce. Abychom mohli se stanicemi v programu rozumně zacházet, potřebujeme datovou strukturu, která by nám převáděla jména stanic na souvislý interval přirozených čísel a naopak. Jinými slovy: potřebujeme černou skříňku, která by uměla operace:
| int Insert(char *s); | přidá řetězec s a vrátí jeho index, jestliže řetězec již existuje, vrátí -1. |
| int Find(char *s); | najde řetězec s a vrátí jeho index, jestliže řetězec neexistuje, vrátí -1. |
| char *Fetch(int i); | vrátí řetězec s indexem i. |
Pro operaci Fetch je asi nejlepší udržovat normální pole s odkazy na
řetězce. Problém je s operacemi Insert a Find. Někteří z vás si jména
udržovali v seznamu, který pak prohledávali. Vyskytla se řešení, která
používala vyhledávací stromy – to je dobré řešení odpovídající standardu
semináře. V praxi by se s největší pravděpodobností použilo hašování.
Průměrné časové složitosti jednotlivých operací (n je počet stanic,
l délka jména stanice):
| Insert | Find | Fetch | |
| Seznam | O(1) | O(n·l) | O(1) |
| Setříděný seznam | O(n+l log n) | O(l log n) | O(1) |
| Bin. vyhl. strom | O(log n) | O(log n) | O(1) |
| Hašování | O(l) | O(l) | O(1) |
Je dobré si uvědomit, že úloha má vlastně dvě části: načtení jízdního řádu a vlastní vyhledávání. Měli bychom optimalizovat rychlost vyhledávání optimálního spojení, které se bude asi provádět mnohokrát, proti rychlosti načtení jízdního řádu, které probíhá pouze jednou při startu programu.
Dále potřebujeme nějakou datovou strukturu pro uložení jízdního řádu. Jízdní řád není rozumné ukládat do normální matice n ×n, kde n je počet stanic, jak je tomu v grafových úlohách zvykem. V jednom políčku takové matice může být více záznamů, protože mezi dvěma stanicemi může jezdit více vlaků v různých časech. Navíc by, vzhledem k realitě, byla tato matice řídká (obsahovala by mnoho prázdných prvků).
Od datové struktury pro uložení jízdního řádu potřebujeme pouze, aby nám k dané stanici vrátila všechny vlaky, které z ní vyjíždějí. To se dá realizovat jako pole ukazatelů na pole následujících struktur:
struct ScheduleItem {
Train train; // číslo vlaku
Time departure, arrive; // čas odjezdu, čas příjezdu do další stanice
Station next; } // číslo další stanice
Pro každou stanici nás pak zajímá těchto struktur ukončený fiktivním vlakem s číslem nula.
Pro samotné vyhledávání potřebujeme datovou strukturu, která by nám umožnila rychle vybrat vrchol s minimálním ohodnocením z dočasně ohodnocených vrcholů. Můžeme použít pole, které budeme při hledání minima celé prohledávat. Lepší řešení je použít vyhledávací strom, ve kterém budeme mít minimum vždy v nejlevějším listu.
Nejlepší je použít datovou strukturu, která je na daný problém specializovaná – haldu:
| void Insert(void *a); | vloží do haldy prvek a |
| void *DeleteMin(); | vrátí prvek s minimální hodnotou a z haldy ho vyřadí, vrátí nil, když je halda prázdná. |
| void Decrease(void *a); | znovu zatřídí do haldy prvek a po snížení jeho ohodnocení. |
Nejznámnější je asi jednostromová binární halda, kterou používá algoritmus HeapSort. Tuto haldu ale nemůžeme použít, protože neumožňuje provádět operaci Decrease v rozumném čase. Řešením je použít Fibonacciho haldu, jejíž popis publikovali v roce 1984 pánové Fredman a Tarjan.
Průměrné časové složitosti jednotlivých operací:
| Insert | DeleteMin | Decrease | |
| Pole | O(1) | O(n) | O(1) |
| Bin. vyhl. strom | O(log n) | O(log n) | O(log n) |
| Fibonacciho halda | O(1) | O(log n) | O(1) |
Následuje kostra programu v C++. Domníváme se, že nemá smysl uvádět výpis
kódu pro práci s triviálními datovými strukturami. Na druhou stranu přesný
popis použitých chytrých datových struktur přesahuje rámec semináře.
Odhadneme-li počty provádění jednotlivých operací na datových strukturách, dostaneme při použití chytrých datových struktur lineární časovou složitost vzhledem k "velikosti" jízdního řádu (za předpokladu, že jízdní řád je velký alespoň n· log n, kde n je počet stanic). Řádově stejnou, ale ve skutečnosti konstanta-krát větší časovou složitost dostaneme, i když budeme místo chytrých datových struktur používat pouze stromy.
Jelikož se datové struktury potřebují docela často, programují je lidé jako samostatné moduly. Po světě běhá mnoho více či méně povedených knihoven pro práci s datovými strukturami. Nejznámější z nich je asi Standard Template Library (STL), kterou naprogramovali pánové Alexander Stepanov a Meng Lee z Hewlett-Packard Laboratories v roce 1994.
Literatura:
- Toepfer Pavel: Algoritmy a programovací techniky, Prometheus Praha, 1995
- Kurt Mehlhorn: Data Structures and Algorithms
8-5-5 Automata finita (Zadání)
Jelikož se jednalo o poslední sérii, došlých řešení bylo vskutku pomálu. Asi se na tom podepsaly probíhající maturity. Většina došlých řešení byla za to správně.
Jediné drobné chyby, kterých jste se hojně dopouštěli v první části, tj. v automatu pro nevnořený komentář, bylo, že po načtení "pravděpodobně ukončovací hvězdičky" jste se nesprávně vraceli do předchozího stavu, pokud přišla další hvězdička, místo abyste zůstali v tomto stavu.
Jinak byl automat extrémě jednoduchý, a opět k němu není potřeba nic dodávat.
| KA | = (Σ, Q, δ, D0, F ) |
| Σ | = ASCII |
| Q | = { D0, D1, D2, D3, D4 } |
| F | = { D4 } |
| δ(D0, /)=D1 | δ(D3, /)=D4 |
| δ(D1, *)=D2 | δ(D3, *)=D3 |
| δ(D2, *)=D3 | δ(D3, ?)=D2 |
| δ(D2, ?)=D3 |
Přičemž `?' jest libovolný jinak neošetřený znak.
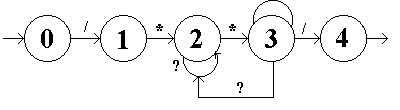
Konečný automat pro vnořené komentáře, jak vetšina z vás správně zjistila nemůže samozřejmě existovat. Dá se to opět ukázat způsobem, jakým jsme ukazovali, že jazyk slov 0i1i není přijímán žádným konečným automatem.
Předpokládejme, že bychom měli automat pro vnořené komentáře. Ten má nějakých, řekněme, n stavů. Podívejme se, kam se automat dostane po přečtení následujících slov:
/*/*/*/*/*/*..... ..... ...../*/*/*/*…/*(n+1-krát)
Nutně některá dvě slova z výše uvedených ho převedou do stejného stavu (stavů je n, slov je n+1). Tato dvě slova mají délku řekněmě 2a a 2b. A teď pozor, přichází zlatý hřeb programu!
Slova (/*)a(*/)a a (/*)b(*/)a převedou tedy
automat nutně též do stejného stavu, tedy buď obě akceptuje, nebo obě
odmítne. V každém případě se pro jedno z nich zachová špatně, neboť jedno
je vnořený komentář a druhé není.
Náš automat tedy pracuje špatně a není to tedy automat pro požadovaný jazyk. Žádný takový automat tedy neexistuje.