Pátá série osmého ročníku KSP
- Termín série: 16. května 1996
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 8-5-1: Rozmarný princ
- 8-5-2: Telefon do pekla
- 8-5-3: Pomsta šíleného zahradníka
- 8-5-4: Čekej, Snad Dojede
- 8-5-5: Automata finita
8-5-1 Rozmarný princ (12 bodů)
Bylo-nebylo. V jednom malém království pod vysokými horami žil krásný princ, jemuž se neustále dvořily princezny. Dokonce se mu dvořila i rozmarná princezna z království za horami, která byla ošklivá a hloupá k tomu. Prince již pomalu začínaly davy vdavek (i říše) chtivých princezen nudit, a tak se poradil se svým komořím-matfyzákem a vymysleli si hru, kterou si s ním měla každá princezna ucházející se o jeho přízeň zahrát. Princezny potom samozřejmě neměly šanci, ale byly ochotny zaplatit za každý nápad, jak prince porazit.
Vaším úkolem je napsat pro princeznu program a popis strategie (algoritmu), jenž jí pomůže vyhrát, pokud to ovšem lze. Napište též, je-li (a pokud ano, tak kdy a v kterém tahu) možné v průběhu hry říci, že princezna, která používá vaši strategii, vyhraje, a složitost vašeho algoritmu.
Pravidla: Zda začíná princezna nebo princ, určí se losem. Na začátku je náhodně zvolen počet hromádek (1 až 10), počet sirek na každé z nich (na počátku všech stejně, a to 1 až 1000) a kolik sirek lze maximálně najednou odebrat z jedné hromádky (1 až 10). Poté začne hra a oba hráči se střídají v odebírání sirek z hromádek. V jednom tahu smí hráč odebírat vždy jen z jedné hromádky alespoň jednu a nejvýše onen zvolený počet sirek. Kdo odebere poslední sirku z libovolné hromádky, prohrál.
8-5-2 Telefon do pekla (11 bodů)
V pekle se rozhodli, že si zavedou telefon. Nejprve všude natahali telefonní kabely, každý obsahoval stínění a kolem stovky drátů. Když se snažili kabely připojit k telefonní ústředně, s hrůzou, jaká je pouze peklu vlastní, zjistili, že nevědí, který drát na jednom konci odpovídá kterému na konci druhém (jen stínění bylo zcela jasně propojeno, neboť bylo pouze jedno). Navíc ještě některé dráty, ač vodit měly, prokazatelně nevodily. Dospěli tedy k závěru, že by si měli postavit speciální testovací zařízení, které bude na jednom konci umět připojovat napájecí napětí k jednotlivým drátům (jako zem se použije stínění) a na druhém konci napětí měřit. Vypadalo tedy asi takto:
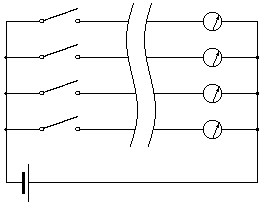
Vás si najali jakožto proslulé odborníky přes programování (jistě jste neodmítli, neboť mít protekci v pekle není od věci), abyste vymysleli algoritmus pro optimální obsluhu tohoto testeru – tedy takový, který použije co nejmenší počet kroků k tomu, aby zjistil propojení všech drátů v kabelu a které dráty jsou nevodivé.
Na počátku je dán počet drátů N (pro oba konce kabelu stejný) a
všechny vypínače jsou ve vypnutém stavu. Program v každém kroku vydá příkaz
k přivedení napětí na drát (`+X', kde X je číslo drátu),
k odpojení napětí od drátu (`-X') či ke změření napětí na druhém konci
(`?X'). Uživatel na každý příkaz `?' odpoví `+' nebo `-' podle
toho, zda nějaké nenulové napětí naměří či nikoliv. Až si bude program jist
výsledkem, vypíše pro každý drát `X -> Y', pokud je drát X na jednom
konci připojen k drátu Y na konci druhém, přičemž nepřipojené dráty
vynechá.
8-5-3 Pomsta šíleného zahradníka (12 bodů)
Jeden zahradník pěstoval stromy. A to ne ledajaké – byly to stromy binární. Pokud přesně nevíte, co je to binární (přesněji binární kořenový) strom, pak vězte, že:
- Prázdná množina je binární strom.
- Jsou-li x a y binární stromy, pak (x,y) je též binární strom.
- Žádné jiné binární stromy neexistují.
Tedy například ((({},{} ), {} ), ({}, {} ) ) , (({}, ({}, {} ) ), ({}, {} ) ) a (({}, {} ), ({}, {} ) ) jsou binární stromy. Trochu názornější je obvyklá grafická podoba – podle jejího vzezření se též stromy jmenují. Naše ukázky by vypadaly takto:
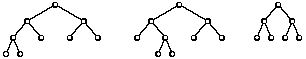
O dvou binárních stromech x a y náš zahradník říkal, že jsou isomorfní, pokud se liší pouze natočením větví – tento vztah značil x ≈ y. Exaktně to lze definovat splněním alespoň jedné z následujícich podmínek:
- x = y = {}
- x = (a, b ), y = (c, d ), a ≈ c, b ≈ d
- x = (a, b ), y = (c, d ), a ≈ d, b ≈ c
Z našich ukázek jsou první a druhý strom navzájem isomorfní, zatímco třetí není isomorfní s žádným jiným.
Napište program, který našemu zahradníkovi pro dva zadané binární stromy určí, zda jsou isomorfní či nikoliv.
8-5-4 Čekej, Snad Dojede (12 bodů)
V jednom bývalém království měli přeslavnou železniční síť. Vlaky jezdily z místa na místo, ba dokonce, ať tomu věříte či nikoliv, dodržovaly jízdní řády. Nicméně síť tratí byla tak složitá, že téměř nikdo nedokázal nalézt rozumné spojení z jednoho města do druhého.
Pro každý vlak je známo jeho číslo (1 až 9999), počáteční i cílová stanice, jakož i všechny další, v nichž staví, spolu s příslušnými časy (čas příjezdu a čas odjezdu pro každou stanici). Jména stanic jsou až 16-znakové jednoznačné řetězce. Mezi nádražími není možno cestovat jinak než železnicí. Na přestup je potřeba vždy alespoň jedna minuta (tedy přijede-li vlak v 15.20, můžete odjet až v 15.21).
Napište program, který načte popis železniční sítě ve zmíněném formátu a poté odpovídá na dotazy všetečných cestujících, jak se v nejkratším možném čase dostat ze stanice A do stanice B (ve stanici A jsme v daném čase t). Pro každé řešení nechť program vypíše seznam stanic, v nichž budou použité vlaky stavět, spolu s časem příjezdu, časem odjezdu a číslem vlaku, jímž stanici opustíme. Pokud je více stejně rychlých řešení, stačí vypsat pouze jedno.
8-5-5 Automata finita (10 bodů)
Jistě všichni dychtivě očekáváte, že na tomoto místě naleznete zadání dalšího konečného automatu. Dlouho jsme přemýšleli, jaký automat vám zadat, když už vlastně z předešlé série máte program, který vám je bryskně generuje a už o nich všechno podstatné víte.
Naštestí jsme nakonec přeci jen nalezli vhodné zadání. Tady tedy je:
- Sestrojte konečný automat, který rozpoznává Céčkové komentáře. Céčkový
komentář je slovo ze znaků ASCII, které začíná posloupností znaků `
/*' a končí posloupností znaků `*/', přičemž uvnitř neobsahuje `*/'. `/*/' se nepovažuje za Céčkový komentář. - Sestrojte konečný automat rozpoznávající Céčkové komentáře
s vnořením definované takto:
- Každý Céčkový komentář je také vnořeným Céčkovým komentářem, pokud neobsahuje
poslopunost znaků `
/*' vyjma svých uvozovačů. - Dále je to každé slovo z ASCII znaků, které začíná a končí
posloupnostmi `
/*' a `*/' a které, mimo jiné, může obsahovat další Céčkové komentáře s vnořením a neobsahuje `/*' ani `*/' jinde než v těchto vnořených komentářích a svých uvozovačích. - Jiné Céčkové komentáře s vnořením nejsou.
- Každý Céčkový komentář je také vnořeným Céčkovým komentářem, pokud neobsahuje
poslopunost znaků `
Tedy například (každý řádek je chápán samostatně):
/* toto je komentar */
/* toto (**) je take /* komentar */
/* toto neni */ komentar */
/* ani toto */ /* komentar neni */
toto neni komentar ani nahodou
Či pro druhou podúlohu:
/* toto je komentar */
/* toto neni /* komentar */
/* toto také neni */ komentar */
/* toto /* je */ /* komentar */ */
/* toto /* je /*take*/ *//*komentar*/ */
/* a /* toto */ pro */ zmenu */ neni*/