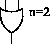Druhá série dvacátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 20-2-1: Volba šamana
- 20-2-2: Setříděné stromy
- 20-2-3: Morzeovkabezoddělovačů
- 20-2-4: Slovíčkaření
- 20-2-5: Hroší ohrádka
- 20-2-6: Hrady, hrádky, hradla
20-2-1 Volba šamana (Zadání)
Nejjednodušší způsob, jak najít šamana, je nejspíš tento: V prvním mezičase mezi údery bubnu každý elf vytvoří zprávu obsahující jeho jméno a věk a sdělí ji svému sousedovi vlevo. V dalších mezičasech elfové pouze přeposílají poslední přijaté zprávy, a to tak dlouho, než jim přijde jejich původní zpráva (poznají ji podle svého jména). To se stane u všech elfů najednou, protože každá zpráva obejde celé kolo elfů za stejnou dobu. Takže skončí všichni současně. Když si každý elf bude ještě pamatovat zprávu nejstaršího dosud známého elfa, bude na konci rituálu znát jméno a věk šamana, protože každá zpráva (včetně té od budoucího šamana) obešla všechny elfy.
Tímto postupem bude celý rituál s N elfy trvat N úderů bubnu. Jak si mnozí řešitelé všimli, je možné rituál dvakrát zrychlit, když budou elfové svoje zprávy posílat oběma směry. V takovém případě stačí, když zpráva obejde půl kola, a rituál bude trvat jenom N/2 úderů. Zbývá vyřešit ukončení rituálu. Pokud je počet elfů v kruhu sudý, pozná se konec jednoduše tak, že ke každému elfovi dojde z obou stran stejná zpráva. Pokud je elfů lichý počet, sejdou se obě kopie zprávy jakoby na půl cesty mezi dvěma elfy. Elf v jednom kroku dostane stejnou zprávu, jakou právě odeslal. Elfové sice neví, jestli jich je sudý nebo lichý počet, ale skončí jednoduše tehdy, když nastane jeden z těchto případů.
20-2-2 Setříděné stromy (Zadání)
Temný mág by z Vás měl radost. Většina došlých řešení potřebovala O(log2 K) porovnání. Ukážeme si zde jedno, které je sice trochu delší na rozbor, ale porovnává stromy opravdu nejméně a dokážeme si to o něm. Nejdříve tři drobná pozorování.
Pokud je délka první resp. druhé řady stromů N1, resp. N2 větší než K, můžeme prvky, které jsou v ní více než K-té, zahodit, jelikož určitě nebudou K-té celkově.
Dále K-tý nejvyšší strom existuje práve tehdy když N1 + N2 ≥ K. Pokud tedy N1 + N2 < K vypíšeme, že strom neexistuje a jsme hotovi. Zřejmě jsme tohle byli schopni udělat bez porovnávání výšek stromů a tedy lépe to nešlo.
Porobně triviální případ nastane, když jedna z posloupností bude mít nulovou délku. Pak K-tý strom celkově bude samozřejmě K-tý v řadě stromů s nenulovou délkou. Tím jsme odstranili speciální případy a dále budeme pokračovat s posloupnostmi, pro jejichž délky platí 1 ≤ N1 ≤ K, 1 ≤ N2 ≤ K a N1 + N2 ≥ K.
Nyní se dostáváme k vlastnímu algoritmu. Ten je založen na metodě půlení intervalů. Bohužel, pokud chceme mít opravdu optimální řešení, tak se nám toto půlení intervalů rozpadne na 3 případy, které sice budou skoro stejné na naprogramování, nicméně, zvláště u třetího, se budou lišit interpretací toho, co které proměnná znamená. Pokud Vás tedy bude zajímat jen idea programu, stačí si přečíst jen první z nich.
Nejdříve případ kdy N1 = N2 = K. Tady si budeme udržovat v paměti o kterých stromech Z1, resp. Z2 z první, resp. druhé posloupnosti budeme vědět, že jsou celkově méně než K-té v pořadí. Dále budeme mít v paměti délku intervalu D, kde ještě K-tý nejvyšší strom může být (budou v úvahu připadat stromy Z1+1, Z1+2, … ,Z1+D z první, resp. Z2+1, Z2+2, … ,Z2+D z druhé řady). Na D je také možno se dívat jako na počet stromů, které jsou celkově nejvýše K-té, ale které jsme zatím ještě nenašli (rozuměmne které jsou více než Z1., resp. Z2. v první, resp. druhé řadě). Z tohoto úhlu pohledu je zřejmé interpretace součtu Z1 + Z2 + D, který bude po celou dobu běhu programu roven K. Na počátku zřejmě Z1 = Z2 = 0 (a nula tady znamená, že i první strom v příslušné posloupnosti může být K-tý nejvyšší) a D = K.
Nyní k vlastnímu půlení intervalů. Vezměme z první, resp. druhé řady strom s pořadím S1 = Z1 + ⌊D/2 ⌋, resp. S2 = Z2 + ⌊D/2 ⌋. Tyhle dva stromy budeme muset porovnat. BÚNO nechť je vyšší první z nich. To znamená, že z druhé řady mohou být vyšší než strom S1 jen stromy 1, 2, … , S2-1. Nicméně jak víme, tak S1 + S2-1 ≤ K-1 a tedy strom S1 může být celkově nejvýše (K-1)-ní. Tím jsme o něm dokázali, že musí být před tím, který hledáme a tak můžeme prohlásit, že Z1 = S1. Tím jsme vyloučili další stromy a tak musíme zkrátit i interval D, ve kterém hledáme, konkrétně na ⌈D/2 ⌉. Jak se můžeme snadno přesvědčit, bude opět platit Z1 + Z2 + D = K.
Předchozí odstavec budeme opakovat dokud D > 1. Pak budeme mít o Z1 + Z2 = K-1 stromech dokázáno, že jsou nejvýše (K-1)-ní a tedy K-tý strom v pořadí bude vyšší z dvojice stromů Z1 + 1 a Z2 + 1.
Nyní k důkazu optimality tohoto případu. X dotazy na porovnání výšek stromů můžeme rozlišit mezi 2X možnostmi (máme jen 2 možné odpovědí - je vyšší první, resp. druhý strom). Rozhodujeme se mezi 2K stromy a tak potřebujeme alespoň ⌈ log2(2K) ⌉= ⌈(log2 K) ⌉+ 1 porovnání. Náš program bude ⌈ log2 K ⌉-krát porovnávat během cyklu a pak bude jedno porovnání na rozhodnutí, zda je K-tý nejvyšší strom v první, resp. druhé řadě.
Druhý uvažovaný případ nastane, když N1 = K a N2 < K (nebo obráceně). Tady můžeme vyloučit na začátku stromy 1, 2, … , K - N2 - 1 z první řady aniž bychom potřebovali provnávat - v druhé řadě prostě není dost stromů na to, aby byly celkově K-té. Tím máme v první řadě N2 + 1 stromů, které mají naději stát se K-tým nejvyšším, zatímco v druhé řadě je jich jen N2. Zavedeme si tedy v druhé řadě virtuální (N2 + 1)-ní strom, který bude nižší než jakýkoliv jiný (v programu je tohle implementováno ve funkci porovnávající stromy), čímž délky obou intervalů srovnáme a můžeme použít výše uvedené půlení intervalů, kde ale počáteční podmínky budou Z1 = K - N2 - 1, Z2 = 0 a D = N2 + 1.
Důkaz optimality bude analogický. Vybíráme z 2 N2 + 1 stromů, budeme tedy potřebovat ⌈ log2(2 N2 + 1) ⌉ dotazů. Program bude chtít porovnat ⌈ log2 (N2 + 1) ⌉-krát během cyklu a jednou na rozhodnutí, ve které ze zadaných dvou řad hledaný strom je. Tato dvě čísla jsou shodná, ač to na první pohled není vidět. Pro naše N2 je ⌈ log2(2 N2 + 1) ⌉= ⌈ log2 (2 N2 + 2) ⌉= ⌈ log2 (N2 + 1) ⌉+1. První rovnost neplatí obecně, nicméně my víme, že N2 je přirozené číslo. Tedy 2 N2 + 1 je číslo liché větší než 2 proto je horní celá část binárního logaritmu stejná jako horní celá část binárního logaritmu čísla o 1 vyššího. (Kdybychom si nakreslili graf funkce f(x) = ⌈ log2(x) ⌉, tak by vypadal jako konstantní funkce až na body, které jsou mocninou dvojky, kde f(x) zvyšuje skokově svou hodnotu o 1. Nicméně mocniny dvojky větší než dva jsou sudé.)
Zbývá posletní případ, kdy N1 < K a N2 < K. Tady budeme moci i bez porovnávání tvrdit, že stromy 1, 2, … , K - 1 - N2 v první, resp. 1, 2, … , K - 1 - N1 v druhé řadě budou v celkovém pořadí maximálně (K-1)-ní a tedy je můžeme vyloučit rovnou. Analogicky k předchozímu případu bychom tedy dosadili Z1 = K - 1 - N2, Z1 = K - 1 - N1 a D = N1 + N2 - K + 2. Tohle samořejmě vede k řešení s logaritmickým počtem dotazů, bohužel v některých případech bude chtít měřit jednou navíc. Vybíráme totiž z 2·(N1 + N2 - K + 1) stromů (a tedy optimální počet porovnání je ⌈ log2(2·(N1 + N2 - K + 1) )⌉ )a přímočaře zobecněný postup použitý v předchozich dvou případech vede na ⌈ log2(N1 + N2 - K + 2) ⌉+ 1 porovnání.
Vylepšení na optimální počet porovnání je trochu trik. Místo toho, abychom hledali K-tý nejvyšší prvek, budeme hledat (K+1)-ní. Zřejmě budeme tedy mít u výše uvedeného algoritmu počáteční podmínky Z1 = K - N1, Z2 = K - N2 a D = N1 + N2 - K + 1. Po skončení cyklu bude platit Z1 + Z2 = K víme, že (K+1)-ní nejvyšší storm je vyšší ze stromů Z1 + 1 a Z2 + 1. Co si ale můžeme dovolit tvrdit dále je, že K-tý nejvyšší je nižší ze stromů Z1 a Z2. Důkaz toho je jednoduchý - víme, že všechny stromy, které jsou nejvýše K-té nejvyšší jsou 1, 2, … Z1 v první, resp. 1, 2, … Z2 v druhé řadě. K-tý nejvyšší musí tedy i K-tý nejvyšší být mezi nimi a kvůli setřízenosti vstupních posloupností bude na konci jedné z nich.
Tenhle „trikový“ postup potřebuje ⌈ log2(N1 + N2 - K + 1) ⌉ dodazů během cyklu a jeden dotaz na rozhodnutí se mezi stromy Z1 a Z2. To je ale přesně, jak již bylo uvedeno, minimální počet dotazů potřebných k určení K-tého nejvyššího stromu.
20-2-3 Morzeovkabezoddělovačů (Zadání)
Telegraficky: -..-.---..---..-.-.-.--.-.... :-)
Dobrá, tak trochu podrobněji …
První pokus: Kdybychom chtěli zjistit jen to, zda se zadaný řetězec teček a čárek dá rozložit na slova (tedy aniž bychom uvažovali nad tím, jaká možnost je nejkratší), stačilo by vyzkoušet všechna slova, která pasují na začátek řetězce, a pro každou z těchto možností si zavolat tutéž funkci rekurzivně na zbytek řetězce.
To samozřejmě funguje, jenže někdy až exponenciálně pomalu: pokud budeme
mít ve slovníku slova e (.) a i (..) a vstupní řetězec bude obsahovat spoustu
teček a nakonec čárku, náš algoritmus postupně vyzkouší všechny možnosti, jak
tečky rozložit na e-čka a i-čka, a při každé z nich se zarazí o koncovou
čárku a se svěšeným ocasem se vrátí zpět. Spočítat, kolik přesně těch možností pro
n teček bude, není úplně jednoduché (mimochodem, je to (n+1)-ní Fibonacciho
číslo), ale je jich určitě aspoň 2n/2. To proto, že když si vezmeme
nějakou posloupnost n/2 znaků složenou libovolně z e-ček a i-ček, bude
její morseovkový zápis tvořen nejvýše n tečkami. Všechny takové posloupnosti
(a těch je 2n/2) náš algoritmus určitě vyzkouší a ještě i mnohé další. Nic moc.
Druhý pokus: Použijeme dynamické programování (trochu netradičně odzadu, brzy bude jasné, proč). Nechť vstupní řetězec obsahuje n morseovkových značek z1,… ,zn. My svou úlohu zkusíme vyřešit postupně pro všechny jeho konce: Budeme počítat hodnoty bi, které budou říkat, na kolik nejméně slov se dá rozložit úsek zi,… ,zn, případně nějaké ∞ (tedy chci říci hrozně velké číslo), pokud se úsek rozložit nedá.
Všimneme si, že tato bi se dají docela snadno spočítat pozpátku: Začneme trochu šalamounsky u bn+1 – to je vždy nula, protože prázdnou posloupnost značek můžeme určitě rozložit na prázdnou posloupnost slov. Dále bn je buďto 1 (to pokud poslední značka odpovídá nějakému jednopísmenkovému slovu ve slovníku) nebo ∞ (pokud ne). Pokud už máme spočítaná bi+1,… ,bn+1, snadno dopočítáme bi: Každý rozklad značek od zi do konce musí začínat nějakým slovem, řekněme délky ℓ značek, a pokračovat rozkladem značek od zi+ℓ do konce. Stačí tedy prozkoumat všechna slova, která do vstupu pasují od i-té pozice, a pro každou z nich se podívat, jestli umíme rozložit zbytek (to nám řekne bi+ℓ). Pokud je možností víc, vybereme si samozřejmě tu s nejmenším počtem slov (a tedy nejmenším bi+ℓ). Jinými slovy (ehm, znaky…):
Takto se postupně dopočítáme až k b1, což je minimální počet slov, ze kterých se dá poskládat celý vstup, a to je skoro řešení naší úlohy. Chybí jen tato slova najít. K tomu stačí, abychom si u každého (konečného) bi ještě zapamatovali, které bylo to slovo, jež jsme na tomto místě napasovali do textu. Tomu říkejme třeba si a jeho délce ℓi.
S těmito informacemi už můžeme rekonstruovat celé řešení (pro změnu odpředu). Našli jsme rozklad s b1 slovy a jeho první slovo je s1. Zbytek řetězce tedy musí být rozložen na b1+ℓ1 slov a první z nich je s1+ℓ1. A tak dále.
Časová složitost se nahlédne snadno. Počítáme celkem n hodnot bi, pro každou z nich zkoušíme nejvýše tolik pasujících slov, kolik je maximální délka L slova ve slovníku (mohlo by sice existovat více slov, která by pan Morse psal stejně, ale z těch nám jistě stačí vyzkoušet jedno jediné). Pokud budeme odvážně předpokládat, že jedno slovo otestujeme v konstantním čase, stojí nás to celkem čas O(nL) a paměť O(n) bez slovníku. Zpětný průchod pak zabere pouze čas O(n) a konstantní paměť.
Jak ale reprezentovat slovník, abychom s ním dokázali pracovat tak rychle, jak jsme slíbili? Pomůže nám datová struktura zvaná trie. To je úplně obyčejný strom, do kterého postupně uložíme všechna známá slova v morseovce tak, že v kořeni se budeme rozhodovat podle první značky, v dalším vrcholu podle druhé značky a tak dále. V každém vrcholu si pak zapamatujeme, která slova tam končí (nezapomeňte, že jich může být víc se stejným zápisem). Každé slovo dokážeme do trie přidat v čase lineárním s jeho délkou, celou strukturu tedy vybudujeme lineárně s velikostí slovníku (čili součtem délek všech slov).
Pro libovolnou posloupnost ℓ značek pak samozřejmě umíme v čase O(ℓ) zjistit, jestli ji máme ve slovníku, ale my jsme přeci slíbili O(1), tak to také dodržíme. Ona totiž slova, která při počítání jednoho bi hledáme, nejsou úplně libovolná. První z nich je jen značka zi, druhé je zizi+1, třetí zizi+1zi+2 atd. Úplně tedy stačí, když si zapamatujeme, kde jsme při hledání předchozího slova ve stromu skončili, a odtamtud popolezeme o krok doleva nebo doprava podle toho, jestli následuje tečka nebo čárka. To nás pro každé slovo opravdu stojí jen konstantní čas. (Vidíte, tady se nám hodilo, že řetězec procházíme zprava doleva, jinak bychom totiž museli mít ve slovníku slova uložená pozpátku, což íntnagele ínen étsijaz.
Celkově náš program spotřebuje čas O(nL+P), kde n je délka vstupního morseovkového řetězce, P celková délka slov ve slovníku a L délka nejdelšího slova.
Poznámka: Někteří z vás chytře využili vyhledávací automat k nalezení všech slov pasujících do textu. Tím se řešení za cenu značného prodloužení potenciálně zrychlí na O(n+P+V), kde V je počet výskytů slovníkových slov v textu. To může být někdy lepší, ale v nejhorším případě může být V≈ nL, takže si obecně nepomůžeme.
 Špek na závěr: Jak elegantně převádět jednotlivá písmena
do morseovky. Jistě bychom si mohli nadefinovat pole řetězců s převody
jednotlivých písmenek, ale přeci si pěkné řešení nezkazíme takovou obludností.
Pomůže dvojková soustava. Místo teček a čárek si představíme nuly a jedničky
a přidáme na začátek jedničku (jinak bychom nepoznali
Špek na závěr: Jak elegantně převádět jednotlivá písmena
do morseovky. Jistě bychom si mohli nadefinovat pole řetězců s převody
jednotlivých písmenek, ale přeci si pěkné řešení nezkazíme takovou obludností.
Pomůže dvojková soustava. Místo teček a čárek si představíme nuly a jedničky
a přidáme na začátek jedničku (jinak bychom nepoznali . od ....). To je
nějaké dvojkové číslo, tak si ho zapíšeme desítkově a až budeme potřebovat
tečky a čárky, budeme toto číslo postupně dělit dvěma a zbytky nám povědí
dvojkové číslice, čili tečky a čárky. Jen jaksi pozpátku – to ovšem nevadí,
tak si ho uložíme obráceně. Radši ukážeme příklad: písmenko a se zapisuje
jako .-. Obrátíme na -., přepíšeme do dvojkové soustavy jako 110, což je
šestka.
P.S.: Jak jste jistě uhodli, telegrafická zpráva na začátku našeho řešení zněla „dynamika a trie“.
20-2-4 Slovíčkaření (Zadání)
Před samotným řešením se zamysleme. Budete mít tisíc ponožek, které jsou úplně stejné, kromě velikosti. Řekněme, že mají celkem čtyři různé velikosti, a vy je máte podle jejich velikosti roztřídit. Pravděpodobně si nikdo z vás nezvolí nějakou ponožku jako medián a nezačne třídit menší vlevo, větší vpravo, ani si jich všech tisíc nerozložíte po podlaze a nebudete je spojovat do dvojic, pak do čtveřic atd. Troufnu si odhadnout, že si zvolíte čtyři přihrádky, a do nich budete ponožky rozřazovat. Ano, toto je nejjednodušší a také nejrychlejší řešení. Takovému postupu se říká přihrádkové třídění, nebo anglicky Bucketsort.
Nyní opusťme ponožky a navraťme se k řetězcům(názvům knih) a významu abecedy. Na moment předpokládejme, že řetězce mají všechny jednotkovou délku. A je jich hodně, s úspěchem můžeme očekávat, že jich je o dost více než prvků abecedy. Zřejmě tedy bude nejvýhodnější zvolit si jednotlivé znaky abecedy jako přihrádky a řetězce do nich „nastrkat“. Označme si N počet řetězců a A počet prvků abecedy. Tento postup od nás vyžadoval přístup k přihrádkám v O(A) a rozřazení řetězců v O(N).
Zobecněme problém pro řetězce stejných délek, ale delších než jedna. Mnohé by asi napadlo roztřídit řetězce podle prvního písmene, tam kde by to nestačilo, tak podle druhého atd. My si ukážeme něco mazanějšího. Použijeme Bucketsort na poslední písmena řetězců a podle nich je roztřídíme. Potom na předposlední písmena, přičemž u řetězců, které připadnou do stejné přihrádky, zachováme pořadí z předchozího třídění. Tím získáme roztřídění řetězců podle posledních dvou písmen. My se ale nezastavíme u předposledního a budeme pokračovat dále směrem kupředu. Po i-tém kroku budeme mít řetězce utříděné podle posledních i znaků. V momentě, kdy se dostaneme k prvnímu písmenu a tedy i se bude rovnat společné délce řetězců, máme vyhráno. Řetězce jsou lexikograficky utříděny. Právě jste se seznámili s Radixsortem.
Přitvrdíme a povolíme řetězcům mít různé délky. Předpokládejme, že bychom řetězce doplnili na stejnou délku nějakým znakem, který by byl lexikograficky menší než všechny prvky abecedy. Fungovalo by to, ale mohli bychom si ošklivě ublížit na časové i paměťové složitosti - například bychom měli milion řetězců délky jedna a jeden délky milion… Naštěstí můžeme správný výsledek získat jedním drobným úskokem. Nejprve si však označme L jako délku nejdelšího z řetězců a P jako součet délek všech řetězců. Pokud si na začátku všechny řetězce setřídíme podle délky (opět přihrádkově), můžeme pak postupovat tak, že v i-tém kroku třídění budeme pracovat pouze s řetězci délky alespoň L-i+1, tedy v prvním kroku pouze s řetězci délky L atd. Provedeme to tak, že v každém kroku roztřídíme do přihrádek nejprve řetězce z minulého třídění a tedy s větší délkou. Potom před ně do přihrádek naskládáme řetězce s délkou právě L-i+1, tedy řetězce, které znakem na zpracovávané pozici končí. Pokud jste uvěřili správnosti Radixsortu, pak je vám nyní jasné, že pomocí tohoto triku opravdu třídíme, a navíc jen tam, kde je to třeba.
Podívejme se, jak rychle takové řešení funguje. Museli jsme provést L kroků (třídíme řetězce od poslední k první pozici). V každém z těchto kroků jsme museli projít přihrádky v setříděném pořadí a inicializovat je v O(A). Tedy tuto část algoritmu provádíme v O(L·A). Určitě se právě ptáte, kampak se schovalo oněch N řetězců a jak to, že netrvá každý krok třídění ve skutečnosti O(A+N), protože až s N řetězci v každém kroku manipulujeme. Pokusme se na to podívat jinak. Díky našemu triku každý řetězec třídíme až tehdy, když je to třeba a má dostatečnou délku. Do té doby s ním nepracujeme. Můžeme tedy tvrdit, že s každým řetězcem pracujeme dohromady tolikrát, kolik má znaků. To v sumě pro všechny řetězce ale znamená O(P). Podobně počáteční setřídění řetězců podle délky je v O(L+N). Celý algoritmus tak běží v O(L·A + P +N) , tj. O(L·A + P). V této knížečce naleznete i vzorovou implementaci. Místo abecedy se v ní uvažují celá čísla v intervalu od 0 do A-1, což ale nijak nevadí, protože každá abeceda, kde lze porovnávat, musí být převeditelná na tento případ.
 Jako vždy existuje ještě o něco zapeklitější, ale o to efektivnější
řešení. Uvědomme si, kde uvedené řešení nejvíce „plýtvá“. V každém kroku
prochází všechny přihrádky, bez ohledu na to, jestli jsme je použili, nebo ne.
Pokud totiž budeme předem znát, které přihrádky jsou použity, můžeme se dívat
pouze do nich a také pouze tyto přihrádky inicializovat a posléze i čistit. Je
však důležité, abychom tyto přihrádky znali v setříděném pořadí, protože je tak
potřebujeme procházet. Nelze ale pro každý krok tuto informaci počítat zvlášť,
protože by to vždy trvalo nejméně O(A) čemuž se snažíme vyhnout. Proto tento
výpočet provedeme na začátku, a to naráz, pro všechny pozice. Uvažujme všechny
dvojice (písmeno, pozice), které se v řetězcích vyskytují. Tyto dvojice na
počátku setřídíme podle písmen. Tím pro každé písmeno budeme vědět, na kterých
pozicích se vyskytuje. Lze si tak vytvořit seznam použitých znaků, pro každou
pozici od 1 do L, prostě tak, že projdeme písmena ve vzestupném pořadí a za
každou pozici, na které se písmeno vyskytne, přidáme toto písmeno na konec
seznamu, který této pozici přísluší. A pak už stačí se při třídění řídit touto
informací. Dvojic je P, jako znaků. Tedy toto počáteční předpočítání stíháme
v O(P+A). Každý krok algoritmu tak už netrvá O(A). Nyní se dohromady ve
všech krocích použije O(P) přihrádek, což je citelně lepší. Tedy výsledná
časová i paměťová složitost je O(N+P+A).
Jako vždy existuje ještě o něco zapeklitější, ale o to efektivnější
řešení. Uvědomme si, kde uvedené řešení nejvíce „plýtvá“. V každém kroku
prochází všechny přihrádky, bez ohledu na to, jestli jsme je použili, nebo ne.
Pokud totiž budeme předem znát, které přihrádky jsou použity, můžeme se dívat
pouze do nich a také pouze tyto přihrádky inicializovat a posléze i čistit. Je
však důležité, abychom tyto přihrádky znali v setříděném pořadí, protože je tak
potřebujeme procházet. Nelze ale pro každý krok tuto informaci počítat zvlášť,
protože by to vždy trvalo nejméně O(A) čemuž se snažíme vyhnout. Proto tento
výpočet provedeme na začátku, a to naráz, pro všechny pozice. Uvažujme všechny
dvojice (písmeno, pozice), které se v řetězcích vyskytují. Tyto dvojice na
počátku setřídíme podle písmen. Tím pro každé písmeno budeme vědět, na kterých
pozicích se vyskytuje. Lze si tak vytvořit seznam použitých znaků, pro každou
pozici od 1 do L, prostě tak, že projdeme písmena ve vzestupném pořadí a za
každou pozici, na které se písmeno vyskytne, přidáme toto písmeno na konec
seznamu, který této pozici přísluší. A pak už stačí se při třídění řídit touto
informací. Dvojic je P, jako znaků. Tedy toto počáteční předpočítání stíháme
v O(P+A). Každý krok algoritmu tak už netrvá O(A). Nyní se dohromady ve
všech krocích použije O(P) přihrádek, což je citelně lepší. Tedy výsledná
časová i paměťová složitost je O(N+P+A).
Tuto úlohu je možno řešit také pomocí struktury zvané trie, která v základním stavu dává O(P·A), ale lze ji také vylepšit výše zmíněným trikem na O(N+P+A).
20-2-5 Hroší ohrádka (Zadání)
Milí chovatelé hrošíků, přestože nikdo z vás nedosáhl maximálního počtu bodů, poradili jste si s řešením Ohrádky velmi dobře. Našim účastníkům, kteří úlohu vyřešili, věnujeme k Vánocům nějaké ty body. Pro všechny ostatní tu máme alespoň návod, jak si Hroší ohrádku postavit.
Než začneme se samotným hledáním konvexního obalu, setřídíme si souřadnice kůlů. Primárně budeme třídit podle souřadnice x vzestupně (tedy abychom měli kůly v rovině setříděné zleva doprava). Kůly se stejnou x-ovou souřadnicí setřídíme podle y opět vzestupně (tedy zdola nahoru). Náš algoritmus by s drobnými úpravami fungoval, i kdybychom kůly setřídili jinak. Takto ale dostaneme výsledná data rovnou v pořadí, které vyžaduje zadání.
Nyní budeme procházet kůly a vytvoříme horní část konvexního obalu. Analogicky pak projdeme kůly ještě jednou a vytvoříme spodní část. Obě části nakonec spojíme a dostaneme výsledný konvexní obal. Zbývá ukázat, jak vytvořit horní část obalu (spodní si ani ukazovat nebudeme – sami si rozmyslete, v čem se bude lišit od horní části).
Na začátku vezmeme první kůl – ten který je nejvíce vlevo (a případně také nejvíce dole). Pak postupně přidáváme další kůly a přitom hlídáme, aby se nám neporušila konvexita. Řekněme, že máme kůly H1, H2, ... Hk, které tvoří začátek horní části konvexního obalu, a právě chceme přidat kůl I. Podíváme se, zda by přidání tohoto kůlu neporušilo konvexnost již hotové části (matematiku okolo si popíšeme za chvíli). V případě, že by nastal problém – tzn. úsečky Hk-1Hk a HkI svírají „špatný“ úhel – vyhodíme Hk z horní části a zkusíme I přidat znovu. Pokud žádný problém nenastane, nebo v horní části je zatím jen jeden kůl, vesele přidáme I.
Nyní nám zbývá vypočítat vzoreček, který bude umět rozhodnout, jaký úhel spolu svírají dvě úsečky. Všiměte si, že nás nezajímá hodnota tohoto úhlu, ale pouze zda je větší nebo menší 180°. Úsečky si pro lepší přehlednost označíme AB a BC (jsou tedy spojeny v bodě B) a Ax budeme značit x-ovou souřadnici bodu A (analogicky pro y-ové souřadnice).
Při pohledu na obrázek není těžké si rozmyslet, že tyto úsečky jsou konvexní, pokud je směrnice první úsečky menší, než směrnice druhé:
| δx(AB) |
| δy(AB) |
| δx(BC) |
| δy(BC) |
Za delty si dosadíme souřadnice bodů:
| Bx - Ax |
| By - Ay |
| Cx - Bx |
| Cy - By |
Abychom se zbavili dělení a nemuseli ošetřovat zvlášť případ, kdy jmenovatel některého zlomku je nulový, rozšíříme si rovnici na tvar:
Z matematického hlediska není výše uvedená úprava úplně vpořádku. Ovšem není těžké si rozmyslet jak se chovají nevhodné případy (tj. By - Ay = 0 nebo Cy - By = 0), a že výsledná rovnice je vlastně to, co jsme celou dobu chtěli.
Nalezenou nerovnici stačí použít jako logickou podmínku, která otestuje, zda jsou dvě úsečky konvexní. Pro spodní část konvexního obalu použijeme stejnou nerovnici, ale s opačnou nerovností.
A nyní se podíváme, jak je na tom časová a paměťová složitost. Někteří čtenáři si možná všimli, že výše popsaný algoritmus vypadá jako backtracking a backtracking je často spojován s exponenciální časovou složitostí. Panika ovšem není na místě, protože náš „skoro-backtracking“ je hodný a pokorně seběhne v lineárním čase. Idea důkazu je jednoduchá. Sice se může stát, že při přidávání některého z kůlů budeme muset hodně kůlů z již hotové části vyhodit, ale na druhou stranu víme, že každý kůl do vytvářené části (horní i dolní) vložíme právě jednou a nejvýše jednou každý kůl vyhodíme. Při počítání složitosti ještě nesmíme zapomenout, že jsme na začátku kůly třídili, a třídění nám zabere O(N · log N). Takže celková časová složitost bude: O(N · log N + N) = O(N · log N).
Paměťová složitost je lineární, protože si potřebujeme pamatovat pouze načtené kůly a vytvářený obal (a obal nemůže obsahovat víc, než původní množství kůlů).
V implementaci bylo potřeba se vypořádat ještě s drobnými
detaily navíc, ale to už si přečtěte přímo ve zdrojovém kódu.
20-2-6 Hrady, hrádky, hradla (Zadání)
V druhé serii našeho seriálu o elektronice, hradlech a radostech podobných jste měli za úkol vymyslet "hromadný" OR. Je mnoho způsobů, jak se dá taková funkce OR realizovat. Jak už je obvyklé, měli jste být při návrhu šetrní a ještě navíc, dokázat že vaše řešení je nejšetrnější. Nejdříve dokážeme, že na spočítání jednoho výstupu z n vstupů potřebujeme nejméně n-1 hradel. Poté ukážeme, že k takovému výpočtu je třeba minimálně logaritmický počet hladin a to ⌈log2(n) ⌉. Následně ukážeme konstrukci takového obvodu pro obecné n.
Začneme nejdříve důkazem minimálního počtu hradel. K dispozici máme jenom a pouze hradla dvouvstupová. Výstupy hradel se dle definice z prvního dílu seriálu spojovat nesmí, proto přidáním hradla můžeme ze dvou "drátu" vyrobit jeden. Naopak rozdvojování "vodičů" nám nijak nepomůže. Tedy obecně pro n "vodičů" na vstupu potřebujeme n-1 hradel abychom je zredukovali postupným přidáváním hradel na jeden výstup.
| n |
| 2 |
| n |
| 22 |
| n |
| 23 |
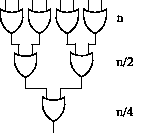 Nyní víme, jaké má mít takový obvod parametry. Zbývá vymyslet, jak vlastně
vypadá. Pro n, jež je mocninou dvojky je konstrukce jednoduchá a přímo plyne z
důkazu minimální hloubky zapojení. V takovém případě bude mít každá hladina
postupně n,
Nyní víme, jaké má mít takový obvod parametry. Zbývá vymyslet, jak vlastně
vypadá. Pro n, jež je mocninou dvojky je konstrukce jednoduchá a přímo plyne z
důkazu minimální hloubky zapojení. V takovém případě bude mít každá hladina
postupně n, | n |
| 2 |
| n |
| 22 |
| n |
| 23 |
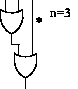
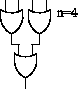
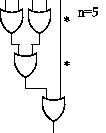
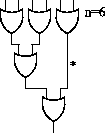
Pro obecné n budeme obvod konstruovat jakoby indukcí. Začneme pro n=2 jedním hradlem OR. Hradla budeme přidávat dle následujících pravidel. Nejdříve si ale zadefinujeme pojem zaplněná hladina. To je taková, jejíž hranicí neprochází vodič. Následně pokud existuje nějaká nezaplněná hladina, přidáme hradlo OR, tak, že prochází drátem, který procházel hranicí hladiny, tím nám přibyde jedno hradlo a jeden vstup, který protáhneme do vstupní hladiny (tím nám může přibýt prázdných hladin). Pokud prázdné hladiny nejsou, přidáme hradlo tak, že bude dělat OR mezi dosavadním výstupem a přidáváným vstupem (tím nám pro n ≠ 2n - 1 jistě vziknou volné hladiny). Na obrázku je prvních pět kroků konstrukce, hvězdičkami jsou označeny volné hladiny.