Recepty z programátorské kuchařky
Grafy

V dnešním vydání známého bestselleru budeme péci grafy souvislé i nesouvislé, orientované i neorientované. Řekneme si o základním procházení grafem, komponentách souvislosti, topologickém uspořádání a dalších grafových algoritmech. Abychom ale mohli začít, musíme si nejprve říci, s čím budeme pracovat.

Ingredience

Neorientovaný graf je určen množinou vrcholů V a množinou hran E, což jsou neuspořádané dvojice vrcholů. Hrana e = {x, y} spojuje vrcholy x a y. Většinou požadujeme, aby hrany nespojovaly vrchol se sebou samým (takovým hranám říkáme smyčky) a aby mezi dvěma vrcholy nevedla více než jedna hrana (pokud toto neplatí, mluvíme o multigrafech). Obvykle také předpokládáme, že vrcholů je konečně mnoho. Neorientovaný graf většinou zobrazujeme jako body pospojované čarami.

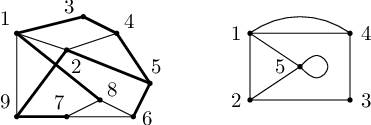
Podgrafem grafu G rozumíme graf G', který vznikl z grafu G vynecháním některých (a nebo žádných) hran a vrcholů.

Často nás zajímá, zda se dá z vrcholu x dojít po hranách do vrcholu y. Ovšem slovo „dojít“ by mohlo být trochu zavádějící, proto si zavedeme pár pojmů:

• sled budeme říkat takové posloupnosti vrcholů a hran tvaru v₁, e₁, v₂, e₂, …, e_n-1, v_n, že e_i={v_i,v_i+1} pro každé i. Sled je tedy nějaká procházka po grafu. Délku sledu měříme počtem hran v této posloupnosti.
• tah je sled, ve kterém se neopakují hrany, tedy e_i ≠ e_j pro i ≠ j.
• cesta je sled, ve kterém se neopakují vrcholy, čili v_i ≠ v_j pro i ≠ j. Všimněte si, že se nemohou opakovat ani hrany.

Lehce nahlédneme, že pokud existuje sled z vrcholu x do y (v₁=x, v_n=y), pak také existuje cesta z vrcholu x do vrcholu y. Každý sled, který není cestou, totiž obsahuje nějaký vrchol u dvakrát. Existuje tedy i<j takové, že u = v_i = v_j. Pak ale můžeme z našeho sledu vypustit posloupnost e_i, v_i+1, …, e_j-1, v_j a dostaneme také sled spojující v₁ a v_n, který je určitě kratší než původní sled. Tak můžeme po konečném počtu úprav dospět až ke sledu, který neobsahuje žádný vrchol dvakrát, tedy k cestě.

Kružnicí neboli cyklem nazýváme cestu délky alespoň 3, ve které oproti definici cesty navíc platí v₁ = v_n. Někdy se na cesty, tahy a kružnice v grafu také díváme jako na podgrafy, které získáme tak, že z grafu vypustíme všechny ostatní vrcholy a hrany.

Ještě si ukážeme, že pokud existuje cesta z vrcholu a do vrcholu b a z vrcholu b do vrcholu c, pak také existuje cesta z vrcholu a do vrcholu c. To vyplývá z faktu, že existuje sled z vrcholu a do vrcholu c, který můžeme dostat například tak, že spojíme za sebe cesty z a do b a z b do c. A jak jsme si ukázali, když existuje sled z a do c, existuje i cesta z a do c.

V mnoha grafech (například v těch na předchozím obrázku) je každý vrchol dosažitelný cestou z každého. Takovým grafům budeme říkat souvislé. Pokud je graf nesouvislý, můžeme ho rozložit na části, které již souvislé jsou a mezi kterými nevedou žádné další hrany. Takové podgrafy nazýváme komponentami souvislosti.

Teď se podívejme na pár pojmů z přírody: Strom je souvislý graf, který neobsahuje kružnici. List je vrchol, ze kterého vede pouze jedna hrana. Ukážeme, že každý strom s alespoň dvěma vrcholy má nejméně dva listy. Proč to? Stačí si najít nejdelší cestu (pokud je takových cest více, zvolíme libovolnou z nich). Oba koncové vrcholy této cesty musí být nutně listy: kdyby z některého z nich vedla hrana, musela by vést do vrcholu, který na cestě ještě neleží (jinak by ve stromu byla kružnice), ale o takovou hranu bychom cestu mohli prodloužit, takže by původní cesta nebyla nejdelší.

Grafům bez kružnic budeme obecně říkat lesy, jelikož každá komponenta souvislosti takového grafu je strom.

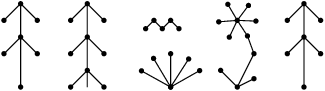
Někdy se hodí jeden z vrcholů stromu prohlásit za kořen, čímž jsme si v každém vrcholu určili směr nahoru (ke kořeni – je to zvláštní, ale matematici obvykle kreslí stromy kořenem vzhůru) a dolů (od kořene). Souseda vrcholu směrem nahoru pak nazýváme jeho otcem, sousedy směrem dolů jeho syny.

Kostra souvislého grafu říkáme každému jeho podgrafu, který je stromem a spojuje všechny vrcholy grafu. Můžeme ji například získat tak, že dokud jsou v grafu kružnice, odebíráme hrany ležící na nějaké kružnici. Pro nesouvislé grafy nazveme kostrou les tvořený kostrami jednotlivých komponent. Na prvním obrázku je jedna z koster levého grafu znázorněna silnými hranami.

Cvičení: Zkuste si dokázat, že stromy jsou právě grafy, které jsou souvislé a mají o jedna méně hran než vrcholů.

Orientované grafy

Často potřebujeme, aby hrany byly pouze jednosměrné. Takovému grafu říkáme orientovaný graf. Hrany jsou nyní uspořádané dvojice vrcholů (x,y) a říkáme, že hrana vede z vrcholu x do vrcholu y. Hrany (x,y) a (y,x) jsou tedy dvě různé hrany. Orientovaný graf většinou zobrazujeme jako body spojené šipkami. Většina pojmů, které jsme definovali pro neorientované grafy, dává smysl i pro grafy orientované, jen si musíme dát pozor na směr hran.

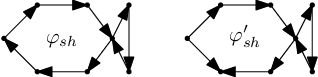
Se souvislostí orientovaných grafů je to trochu složitější. Rozlišujeme slabou a silnou souvislost: slabě souvislý je graf tehdy, pokud se z něj zapomenutím orientace hran stane souvislý neorientovaný graf. Silně souvislým ho nazveme tehdy, vede-li mezi každými dvěma vrcholy x a y orientovaná cesta v obou směrech. Pokud je graf silně souvislý, je i slabě souvislý, ale jak ukazuje náš obrázek, opačně to platit nemusí.

Komponenta silné souvislosti orientovaného grafu G je takový podgraf G', který je silně souvislý a není podgrafem žádného většího silně souvislého podgrafu grafu G. Komponenty silné souvislosti tedy mohou být mezi sebou propojeny, ale žádné dvě nemohou ležet na společném cyklu.

Ohodnocené grafy

Další možností, jak si graf „vyzdobit“, je ohodnotit jeho hrany čísly. Například v grafu silniční sítě (vrcholy jsou města, hrany silnice mezi nimi) je zcela přirozené ohodnotit hrany délkami silnic nebo třeba mýtným vybíraným za průjezd silnicí. Přiřazeným číslům se proto často říká délky hran nebo jejich ceny. Pojmy, které jsme si před chvílí nadefinovali pro obyčejné grafy, můžeme opět snadno rozšířit pro grafy ohodnocené – např. délku sledu budeme namísto počtu hran sledu počítat jako součet jejich ohodnocení. Neohodnocený graf pak odpovídá grafu, v němž mají všechny hrany jednotkovou délku.

Podobně můžeme přiřazovat ohodnocení i vrcholům, ale raději si všechny operace s ohodnocenými grafy necháme na některé z dalších dílů Kuchařky. I tak budeme mít práce dost a dost.

Reprezentace grafů

Nyní už víme o grafech hodně, ale ještě jsme si neřekli, jak graf reprezentovat v paměti počítače. To můžeme udělat například tak, že vrcholy očíslujeme přirozenými čísly od 1 do N, hrany od 1 do M a odkud kam vedou hrany, popíšeme jedním z následujících tří způsobů:

• matice sousednosti – to je pole A velikosti N ×N. Na pozici A[i, j] uložíme hodnotu 0 nebo 1 podle toho, zda z vrcholu i do vrcholu j hrana vede (1), nebo nevede (0). S maticí sousednosti se zachází velmi snadno, ale má tu nevýhodu, že je vždy kvadraticky velká bez ohledu na to, kolik je hran. Výhodou naopak je, že místo jedniček můžeme ukládat nějaké další informace o hranách, třeba jejich délky. Vpravo od tohoto odstavce najdete matici sousednosti grafu z prvního obrázku.

  	123456789
  1	011000011
  2	100110001
  3	100100000
  4	011010000
  5	010101000
  6	000010110
  7	000001011
  8	100001100
  9	110000100

• seznam sousedů je obvykle tvořen dvěma poli: polem sousedů S[1… M] obsahujícím postupně čísla všech vrcholů, do kterých vede hrana z vrcholu 1, pak z vrcholu 2 atd., a polem začátků Z[1… N], v němž se pro každý vrchol dozvíme začátek odpovídajícího úseku v poli S. Pokud navíc do Z[N+1] uložíme M+1, bude platit, že sousedé vrcholu i jsou uloženi v S[Z[i]], …, S[Z[i+1]-1]. Tato reprezentace má tu výhodu, že zabírá pouze prostor O(N+M) a sousedy každého vrcholu máme pěkně pohromadě a nemusíme je hledat. Pro graf z 1. obrázku:
  
  Reprezentace grafu seznamem sousedů
• půlhranami – tato reprezentace se používá tehdy, pokud potřebujeme během výpočtu graf složitě upravovat. Je univerzální, ale dost pracná na naprogramování. Spočívá v tom, že si každou hranu uložíme jako dvě půlhrany (začátek a konec hrany), každý vrchol bude obsahovat spojové seznamy přicházejících a odcházejících půlhran a každá půlhrana bude ukazovat na svou druhou polovici a na vrchol, ze kterého vychází.

V následujících receptech budeme vždy používat seznamy sousedů, poli S budeme říkat sousedi, poli Z zacatky. Pole sousedi bude mít rozsah od 0 do M-1, pole zacatky od 0 do N (kde N je počet vrcholů a M počet hran).

Prohledávání do hloubky

Naše povídání o grafových algoritmech začneme dvěma základními způsoby procházení grafem. K tomu budeme potřebovat dvě podobné jednoduché datové struktury: Fronta je konečná posloupnost prvků, která má označený začátek a konec. Když do ní přidáváme nový prvek, přidáme ho na konec posloupnosti. Když z ní prvek odebíráme, odebereme ten na začátku. Proto se tato struktura anglicky nazývá first in, first out, zkráceně FIFO. Zásobník je také konečná posloupnost prvků se začátkem a koncem, ale zatímco prvky přidáváme také na konec, odebíráme je z téhož konce. Anglický název je (překvapivě) last in, first out, čili LIFO.

Algoritmus prohledávání grafu do hloubky:

1. Na začátku máme v zásobníku pouze vstupní vrchol w. Dále si u každého vrcholu v pamatujeme značku z_v, která říká, zda jsme vrchol již navštívili. Vstupní vrchol je označený, ostatní vrcholy nikoliv.
2. Odebereme vrchol ze zásobníku, nazvěme ho u.
3. Každý neoznačený vrchol, do kterého vede hrana z u, přidáme do zásobníku a označíme.
4. Kroky 2 a 3 opakujeme, dokud není zásobník prázdný.

Na konci algoritmu budou označeny všechny vrcholy dosažitelné z vrcholu w, tedy v případě neorientovaného grafu celá komponenta souvislosti obsahující w. To můžeme snadno dokázat sporem: Předpokládejme, že existuje vrchol x, který není označen, ale do kterého vede cesta z w. Pokud je takových vrcholů více, vezmeme si ten nejbližší k w. Označme si y předchůdce vrcholu x na nejkratší cestě z w; y je určitě označený (jinak by x nebyl nejbližší neoznačený). Vrchol y se tedy musel někdy objevit na zásobníku, tím pádem jsme ho také museli ze zásobníku odebrat a v kroku 3 označit všechny jeho sousedy, tedy i vrchol x, což je ovšem spor.

To, že algoritmus někdy skončí, nahlédneme snadno: v kroku 3 na zásobník přidáváme pouze vrcholy, které dosud nejsou označeny, a hned je značíme. Proto se každý vrchol může na zásobníku objevit nejvýše jednou, a jelikož ve 2. kroku pokaždé odebereme jeden vrchol ze zásobníku, musí vrcholy někdy (konkrétně po nejvýše N opakováních cyklu) dojít. Ve 3. kroku probereme každou hranu grafu nejvýše dvakrát (v každém směru jednou). Časová složitost celého algoritmu je tedy lineární v počtu vrcholů N a počtu hran M, čili O(N+M). Paměťová složitost je stejná, protože si tak jako tak musíme hrany a vrcholy pamatovat a zásobník není větší než paměť na vrcholy.

Prohledávání do hloubky implementujeme nejsnáze rekurzivní funkcí. Jako zásobník v tom případě používáme přímo zásobník programu, kde si program ukládá návratové adresy funkcí. Může to vypadat třeba následovně:

oznacen = [False] * N

def projdi(v):
  oznacen[v] = True
  for i in range(zacatky[v], zacatky[v+1]):
    if not oznacen[sousedi[i]]:
      projdi(sousedi[i])

var Oznacen: array[1..MaxN] of Boolean;

procedure Projdi(V: Integer);
var I: Integer;
begin
  Oznacen[V] := True;
  for I := Zacatky[V] to Zacatky[V+1]-1 do
    if not Oznacen[Sousedi[I]] then
      Projdi(Sousedi[I]);
end;

Rozdělit neorientovaný graf na komponenty souvislosti je pak už jednoduché. Projdeme postupně všechny vrcholy grafu, a pokud nejsou v žádné z dosud označených komponent grafu, přidáme novou komponentu tak, že graf z tohoto vrcholu prohledáme do hloubky. Vrcholy značíme přímo číslem komponenty, do které patří. Protože prohledáváme do hloubky několik oddělených částí grafu, každou se složitostí O(N_i + M_i), kde N_i a M_i je počet vrcholů a hran komponenty, vyjde dohromady složitost O(N + M). Nic nového si ukládat nemusíme, a proto je paměťová složitost stále O(N + M).

def projdi(v):
  komponenta[v] = nova_komponenta
  for i in range(zacatky[v], zacatky[v+1]):
    if komponenta[sousedi[i]] == -1:
      projdi(sousedi[i])

...
for i in range(N):
  komponenta[i] = -1
nova_komponenta = 1
for i in range(N):
  if komponenta[i] == -1:
    projdi(i)
    nova_komponenta += 1
...

var Komponenta: array[1..MaxN] of Integer;
    NovaKomponenta: Integer;

procedure Projdi(V: Integer);
var I: Integer;
begin
  Komponenta[V] := NovaKomponenta;
  for I := Zacatky[V] to Zacatky[V+1]-1 do
    if Komponenta[Sousedi[I]] = -1 then
      Projdi(Sousedi[I]);
end;

var I: Integer;
begin
  ...
  for I := 1 to N do Komponenta[I] := -1;
  NovaKomponenta := 1;
  for I := 1 to N do
    if Komponenta[I] = -1 then
      begin
        Projdi(I);
        Inc(NovaKomponenta);
      end;
  ...
end.

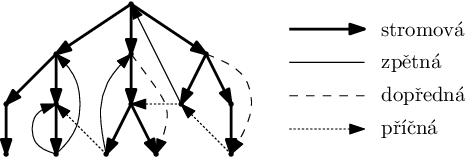
Průběh prohledávání grafu do hloubky můžeme znázornit stromem (říká se mu DFS strom – podle anglického názvu Depth-First Search pro prohledávání do hloubky). Z počátečního vrcholu w učiníme kořen. Pak budeme graf procházet do hloubky a vrcholy zakreslovat jako syny vrcholů, ze kterých jsme přišli. Syny každého vrcholu si uspořádáme v pořadí, v němž jsme je navštívili; tomuto pořadí budeme říkat zleva doprava a také ho tak budeme kreslit. Hranám mezi otci a syny budeme říkat stromové hrany. Protože jsme do žádného vrcholu nešli dvakrát, budou opravdu tvořit strom. Hrany, které vedou do již navštívených vrcholů na cestě, kterou jsme přišli z kořene, nazveme zpětné hrany. Dopředné hrany vedou naopak z vrcholu blíže kořeni do už označeného vrcholu dále od kořene. A konečně příčné hrany vedou mezi dvěma různými podstromy grafu.

Všimněte si, že při prohledávání neorientovaného grafu objevíme každou hranu dvakrát: buďto poprvé jako stromovou a podruhé jako zpětnou, a nebo jednou jako zpětnou a podruhé jako dopřednou. Příčné hrany se objevit nemohou – pokud by příčná hrana vedla doprava, vedla by do dosud neoznačeného vrcholu, takže by se prohledávání vydalo touto hranou a nevznikl by oddělený podstrom; doleva rovněž vést nemůže: představme si stav prohledávání v okamžiku, kdy jsme opouštěli levý vrchol této hrany. Tehdy by naše hrana musela být příčnou vedoucí doprava, ale o té už víme, že neexistuje.

Prohledávání do hloubky lze tedy také využít k nalezení kostry neorientovaného grafu, což je strom, který jsme prošli. Rovnou při tom také zjistíme, zda graf neobsahuje cyklus: to poznáme tak, že nalezneme zpětnou hranu různou od té stromové, po níž jsme do vrcholu přišli.

Pro orientované grafy je situace opět trochu složitější: stromové a dopředné hrany jsou orientované vždy ve stromu shora dolů, zpětné zdola nahoru a příčné hrany mohou existovat, ovšem vždy vedou zprava doleva, čili pouze do podstromů, které jsme již prošli (nahlédneme opět stejně).

Prohledávání do šířky

Prohledávání do šířky je založené na podobné myšlence jako prohledávání do hloubky, pouze místo zásobníku používá frontu:

1. Na začátku máme ve frontě pouze jeden prvek, a to zadaný vrchol w. Dále si u každého vrcholu x pamatujeme číslo H[x]. Všechny vrcholy budou mít na začátku H[x] = -1, jen H[w] = 0.
2. Odebereme vrchol z fronty, označme ho u.
3. Každý vrchol v, do kterého vede hrana z u a jehož H[v] = -1, přidáme do fronty a nastavíme jeho H[v] na H[u] + 1.
4. Kroky 2 a 3 opakujeme, dokud není fronta prázdná.

Podobně jako u prohledávání do hloubky jsme se dostali právě do těch vrcholů, do kterých vede cesta z w (a označili jsme je nezápornými čísly). Rovněž je každému vrcholu přiřazeno nezáporné číslo maximálně jednou. To vše se dokazuje podobně, jako jsme dokázali správnost prohledávání do hloubky.

Vrcholy se stejným číslem tvoří ve frontě jeden souvislý celek, protože nejprve odebereme z fronty všechny vrcholy s číslem n, než začneme odebírat vrcholy s číslem n + 1. Navíc platí, že H[v] udává délku nejkratší cesty z vrcholu w do v. Že neexistuje kratší cesta, dokážeme sporem: Pokud existuje nějaký vrchol v, pro který H[v] neodpovídá délce nejkratší cesty z w do v, čili vzdálenosti D[v], vybereme si z takových v to, jehož D[v] je nejmenší. Pak nalezneme nejkratší cestu z w do v a její předposlední vrchol z. Vrchol z je bližší než v, takže pro něj už musí být D[z]=H[z]. Ovšem když jsme z fronty vrchol z odebírali, museli jsme objevit i jeho souseda v, který ještě nemohl být označený, tudíž jsme mu museli přidělit H[v]=H[z]+1=D[v], a to je spor.

Prohledávání do šířky má časovou složitost taktéž lineární s počtem hran a vrcholů. Na každou hranu se také ptáme dvakrát. Fronta má lineární velikost k počtu vrcholů, takže jsme si oproti prohledávání do hloubky nepohoršili a i paměťová složitost je O(N + M). Algoritmus implementujeme nejsnáze cyklem, který bude pracovat s vrcholy v poli představujícím frontu.

...
for i in range(N):
  H[i] = -1
prvni = 1
posledni = 1
fronta[prvni] = pocatecni_vrchol
H[pocatecni_vrchol] = 0

while True:
  v = fronta[prvni]
  for i in range(zacatky[v], zacatky[v+1]):
    if H[sousedi[i]] < 0:
      H[sousedi[i]] = H[v] + 1
      posledni += 1
      fronta[posledni] = sousedi[i]
  prvni += 1
  if prvni > posledni: break
...

var Fronta, H: array[1..MaxN] of Integer;
    I, V, Prvni, Posledni: Integer;
    PocatecniVrchol: Integer;
begin
  ...
  for I := 1 to N do H[I] := -1;
  Prvni := 1;
  Posledni := 1;
  Fronta[Prvni] := PocatecniVrchol;
  H[PocatecniVrchol] := 0;

  repeat
    V := Fronta[Prvni];
    for I := Zacatky[V] to Zacatky[V+1]-1 do
      if H[Sousedi[I]] < 0 then begin
        H[Sousedi[I]] := H[V]+1;
        Inc(Posledni);
        Fronta[Posledni] := Sousedi[I];
      end;
    Inc(Prvni);
  until Prvni > Posledni;  { Fronta je prázdná }
  ...
end.

Prohledávání do šířky lze také použít na hledání komponent souvislosti a hledání kostry grafu.

Topologické uspořádání

Teď si vysvětlíme, co je topologické uspořádání grafu. Máme orientovaný graf G s N vrcholy a chceme očíslovat vrcholy čísly 1 až N tak, aby všechny hrany vedly z vrcholu s větším číslem do vrcholu s menším číslem, tedy aby pro každou hranu e = (v_i, v_j) bylo i > j. Představme si to jako srovnání vrcholů grafu na přímku tak, aby „šipky“ vedly pouze zprava doleva.

Nejprve si ukážeme, že pro žádný orientovaný graf, který obsahuje cyklus, nelze takovéto topologické pořadí vytvořit. Označme vrcholy cyklu v₁, …, v_n, takže hrana vede z vrcholu v_i do vrcholu v_i-1, resp. z v₁ do v_n. Pak vrchol v₂ musí dostat vyšší číslo než vrchol v₁, v₃ než v₂,… , v_n než v_n-1. Ale vrchol v₁ musí mít zároveň vyšší číslo než v_n, což nelze splnit.

Cyklus je ovšem to jediné, co může existenci topologického uspořádání zabránit. Libovolný acyklický graf lze uspořádat následujícím algoritmem:

1. Na začátku máme orientovaný graf G a proměnnou p = 1.
2. Najdeme takový vrchol v, ze kterého nevede žádná hrana (budeme mu říkat stok). Pokud v grafu žádný stok není, výpočet končí, protože jsme našli cyklus.
3. Odebereme z grafu vrchol v a všechny hrany, které do něj vedou.
4. Přiřadíme vrcholu v číslo p.
5. Proměnnou p zvýšíme o 1.
6. Opakujeme kroky 2 až 5, dokud graf obsahuje alespoň jeden vrchol.

Proč tento algoritmus funguje? Pokud v grafu nalezneme stok, můžeme mu určitě přiřadit číslo menší než všem ostatním vrcholům, protože překážet by nám v tom mohly pouze hrany vedoucí ze stoku ven a ty neexistují. Jakmile stok očíslujeme, můžeme jej z grafu odstranit a pokračovat číslováním ostatních vrcholů. Tento postup musí někdy skončit, jelikož v grafu je pouze konečně mnoho vrcholů.

Zbývá si uvědomit, že v neprázdném grafu, který neobsahuje cyklus, vždy existuje alespoň jeden stok: Vezměme libovolný vrchol v₁. Pokud z něj vede nějaká hrana, pokračujme po ní do nějakého vrcholu v₂, z něj do v₃ atd. Co se při tom může stát?

• Dostaneme se do vrcholu v_i, ze kterého nevede žádná hrana. Vyhráli jsme, máme stok.
• Narazíme na v_i, ve kterém jsme už jednou byli. To by ale znamenalo, že graf obsahuje cyklus, což, jak víme, není pravda.
• Budeme objevovat stále nové a nové vrcholy. V konečném grafu nemožno.

Algoritmus můžeme navíc snadno upravit tak, aby netratil příliš času hledáním vrcholů, z nichž nic nevede – stačí si takové vrcholy pamatovat ve frontě, a kdykoliv nějaký takový vrchol odstraňujeme, zkontrolovat si, zda jsme nějakému jinému vrcholu nezrušili poslední hranu, která z něj vedla, a pokud ano, přidat takový vrchol na konec fronty. Celé topologické třídění pak zvládneme v čase O(N+M).

Jiná možnost je prohledat graf do hloubky a všimnout si, že pořadí, ve kterém jsme se z vrcholů vraceli, je právě topologické pořadí. Pokud zrovna opouštíme nějaký vrchol a číslujeme ho dalším číslem v pořadí, rozmysleme si, jaké druhy hran z něj mohou vést: stromová nebo dopředná hrana vede do vrcholu, kterému jsme již přiřadili nižší číslo, zpětná existovat nemůže (v grafu by byl cyklus) a příčné hrany vedou pouze zprava doleva, takže také do již očíslovaných vrcholů. Časová složitost je opět O(N+M).

def projdi(v):
  # zatím V jen označíme
  ocislovani[v] = 0
  for i in range(zacatky[v], zacatky[v+1]):
    if ocislovani[sousedi[i]] == -1:
      projdi(sousedi[i]]
  posledni += 1
  ocislovani[v] = posledni

...
for i in range(N):
  ocislovani[i] = -1
posledni = 0
for i in range(N):
  if ocislovani[i] == -1:
    projdi(i)
...

var Ocislovani: array[1..MaxN] of Integer;
    Posledni: Integer;
    I: Integer;

procedure Projdi(V: Integer);
var I: Integer;
begin
  Ocislovani[V] := 0; { zatím V jen označíme }
  for I := Zacatky[V] to Zacatky[V+1]-1 do
    if Ocislovani[Sousedi[I]] = -1 then
      Projdi(Sousedi[I]);
  Inc(Posledni);
  Ocislovani[V] := Posledni;
end;

begin
  ...
  for I := 1 to N do
    Ocislovani[I] := -1;
  Posledni := 0;
  for I := 1 to N do
    if Ocislovani[I] = -1 then Projdi(I);
  ...
end.

Hranová a vrcholová 2-souvislost

Nyní se podíváme na trochu komplikovanější formu souvislosti. Říkáme, že neorientovaný graf je hranově 2-souvislý, když platí, že:

• má alespoň 3 vrcholy,
• je souvislý,
• zůstane souvislý po odebrání libovolné hrany.

Na hledání mostů nám poslouží opět upravené prohledávání do hloubky a DFS strom. Všimněme si, že mostem může být jedině stromová hrana – každá jiná hrana totiž leží na nějaké kružnici. Odebráním mostu se graf rozpadne na část obsahující kořen DFS stromu a podstrom „visící“ pod touto hranou. Jediné, co tomu může zabránit, je existence nějaké další hrany mezi podstromem a hlavní částí, což musí být zpětná hrana, navíc taková, která není jenom stromovou hranou viděnou z druhé strany. Takovým hranám budeme říkat ryzí zpětné hrany.

Proto si pro každý vrchol spočítáme hladinu, ve které se nachází (kořen je na hladině 0, jeho synové na hladině 1, jejich synové 2, …). Dále si pro každý vrchol v spočítáme, do jaké nejvyšší hladiny (s nejmenším číslem) vedou ryzí zpětné hrany z podstromu s kořenem v. To můžeme udělat přímo při procházení do hloubky, protože než se vrátíme z v, projdeme celý podstrom pod v. Pokud všechny zpětné hrany vedou do hladiny stejné nebo větší než té, na které je v, pak odebráním hrany vedoucí do v z jeho otce vzniknou dvě komponenty souvislosti, čili tato hrana je mostem. V opačném případě jsme nalezli kružnici, na níž tato hrana leží, takže to most být nemůže. Výjimku tvoří kořen, který žádného otce nemá a nemusíme se o něj proto starat.

Algoritmus je tedy pouhou modifikací procházení do hloubky a má i stejnou časovou a paměťovou složitost O(N + M). Zde jsou důležité části programu:

def projdi(v, nova_hladina):
  hladina[v] = nova_hladina
  spojeno[v] = hladina

  for i in range(zacatky[v], zacatky[v+1]):
    w = sousedi[i]
    if hladina[w] == -1:
      projdi(w, nova_hladina + 1)
      if spojeno[w] < spojeno[v]:
        spojeno[v] = spojeno[w]
      if spojeno[w] > hladina[v]
        dvoj_souvisle = False
    else:
      if hladina[w] < nova_hladina - 1
         and hladina[w] < spojeno[v]:
        spojeno[v] = hladina[w]

...
for i in range(N):
  hladina[i] = -1
dvoj_souvisle = True
projdi(1, 0)
...

var Hladina, Spojeno: array[1..MaxN] of Integer;
    DvojSouvisle: Boolean;
    I: Integer;

procedure Projdi(V, NovaHladina: Integer);
var I, W: Integer;
begin
  Hladina[V] := NovaHladina;
  Spojeno[V] := Hladina[V];

  for I := Zacatky[V] to Zacatky[V+1]-1 do
  begin
    W := Sousedi[I];
    if Hladina[W] = -1 then
    begin { stromová hrana }
      Projdi(W, NovaHladina + 1);
      if Spojeno[W] < Spojeno[V] then
        Spojeno[V] := Spojeno[W];
      if Spojeno[W] > Hladina[V] then
        DvojSouvisle := False; { máme most }
    end
    else { zpětná nebo dopředná hrana }
    if (Hladina[W] < NovaHladina-1) and
       (Hladina[W] < Spojeno[V]) then
      Spojeno[V] := Hladina[W];
  end;
end;

begin
  ...
  for I := 1 to N do
    Hladina[I] := -1;
  DvojSouvisle := True;
  Projdi(1, 0);
  ...
end.

Další formou souvislosti je vrcholová souvislost. Graf je vrcholově 2-souvislý, právě když:

• má alespoň 3 vrcholy,
• je souvislý,
• zůstane souvislý po odebrání libovolného vrcholu.

Algoritmus pro zjištění vrcholové 2-souvislosti grafu je velmi podobný algoritmu na zjišťování hranové 2-souvislosti. Jen si musíme uvědomit, že odebíráme celý vrchol. Ze stromu procházení do hloubky může odebráním vrcholu vzniknout až několik podstromů, které všechny musí být spojeny zpětnou hranou s hlavním stromem. Proto musí zpětné hrany z podstromu určeného vrcholem v vést až nad vrchol v. Speciálně pro kořen nám vychází, že může mít pouze jednoho syna, jinak bychom ho mohli odebrat a vytvořit tak dvě nebo více komponent souvislosti. Algoritmus se od hledání hranové 2-souvislosti liší jedinou změnou ostré nerovnosti na neostrou; sami zkuste najít, které nerovnosti.

Martin Mareš, David Matoušek a Petr Škoda