Recepty z programátorské kuchařky
Třídění
Aktuální verze kuchařky: červenec 2011
Pojem třídění je možná maličko nepřesný, často se však používá. Nehodláme data (čísla, řetězce a jiné) rozdělovat do nějakých tříd, ale přerovnat je do správného pořadí, od nejmenšího po největší – ať už pro nás „větší“ znamená jakékoliv uspořádání.
Se seřazenými údaji se totiž mnohem lépe pracuje. Potřebujeme-li v nich kupříkladu vyhledávat, zvládneme to v uspořádaném stavu mnohem rychleji, jak dosvědčí další kuchařka a běžná zkušenost. Takové uspořádávání dat je proto denním chlebem každého programátora, a tak není divu, že třídící algoritmy jsou jedny z nejstudovanějších.
Obvykle třídíme exempláře datové struktury typu pascalského záznamu (v jiných jazycích struktury, třídy apod.). V takové datové struktuře bývá obsažena jedna význačná položka, klíč, podle které se záznamy řadí. Malinko si svůj život zjednodušíme a budeme předpokládat, že třídíme záznamy obsahující pouze klíč, který je navíc celočíselný – budeme tedy třídít pole celých čísel. Vzhledem k počtu tříděných čísel N pak budeme vyjadřovat časovou (a paměťovou) složitost jednotlivých algoritmů, které si předvedeme.
Dodejme ještě, že se také studují případy, kdy je tříděných dat tolik, že se všechna naráz nevejdou do paměti. Tehdy by nastoupily takzvané vnější třídící algoritmy. Ty dovedou zacházet s daty uloženými třeba na disku a přizpůsobit své chování jeho vlastnostem. Zejména se přizpůsobí tomu, že diskům svědčí spíše sekvenční přístup k datům, zatímco neustálé přeskakování z jednoho konce souboru na druhý je pomalé. Ostatně, i u našeho vnitřního třídění na lokalitě přístupů díky existenci procesorové cache trochu záleží. Toto vše si ale v naší úvodní kuchařce odpustíme.
Přímé metody
Nejjednodušší třídící algoritmy patří do skupiny přímých metod. Jsou krátké, jednoduché a třídí přímo v poli (nepotřebujeme pole pomocné). Tyto algoritmy mají většinou časovou složitost O(N2). Z toho vyplývá, že jsou použitelné tehdy, když tříděných dat není příliš mnoho. Na druhou stranu pokud je dat opravdu málo, je zbytečně složité používat některý z komplikovanějších algoritmů, které si předvedeme později.
Třídění přímým výběrem (SelectSort) je založeno na opakovaném vybírání nejmenšího čísla z dosud nesetříděných čísel. Nalezené číslo prohodíme s prvkem na začátku pole a postup opakujeme, tentokrát s nejmenším číslem na indexech 2, …, N, které prohodíme s druhým prvkem v poli. Poté postup opakujeme s prvky s indexy 3, …,N atd. Je snadné si uvědomit, že když takto postupně vybíráme minimum z menších a menších intervalů, setřídíme celé pole (v i-tém kroku nalezneme i-tý nejmenší prvek a zařadíme ho v poli na pozici s indexem i).
procedure SelectSort(var A: Pole);
var i, j, k, x: integer;
begin
for i:=1 to N-1 do begin
k:=i;
for j:=i+1 to N do
if A[j]<A[k] then k:=j;
x:=A[k]; A[k]:=A[i]; A[i]:=x;
end;
end;
def SelectSort(pole):
k=1
for i in range(0, len(pole)):
k=i
for j in range(i+1, len(pole)):
if pole[j]<pole[k]:
k=j
pole[i],pole[k]=pole[k],pole[i]
Pro úplnost si ještě řekněme pár slov o časové složitosti právě popsaného algoritmu. V i-tém kroku musíme nalézt minimum z N-i+1 čísel, na což spotřebujeme čas O(N-i+1). Ve všech krocích dohromady tedy spotřebujeme čas O(N+(N-1)+… +3+2+1)=O(N2).
Třídění přímým vkládáním (InsertSort) funguje na podobném principu jako třídění přímým výběrem. Na začátku pole vytváříme správně utříděnou posloupnost, kterou postupně rozšiřujeme. Na začátku i-tého kroku má tato utříděná posloupnost délku i-1. V i-tém kroku určíme pozici i-tého čísla v dosud utříděné posloupnosti a zařadíme ho do utříděné posloupnosti (zbytek utříděné posloupnosti se posune o jednu pozici doprava). Není těžké si rozmyslet, že každý krok lze provést v čase O(N). Protože počet kroků algoritmu je N, celková časová složitost právě popsaného algoritmu je opět O(N2).
procedure InsertSort(var A: Pole);
var i, j, x: integer;
begin
for i:=2 to N do begin
x:=A[i];
j:=i-1;
while (j>0) and (x<A[j]) do begin
A[j+1]:=A[j];
j:=j-1;
end;
A[j+1]:=x;
end;
end;
def InsertSort(pole):
for i in range(1,len(pole)):
x=pole[i]
j=i-1
while j>=0 and x<pole[j]:
pole[j+1]=pole[j]
j-=1
pole[j+1]=x
V uvedeném programu je využito zkráceného vyhodnocování v podmínce cyklu
while. To znamená, že testování podmínky je ukončeno, jakmile j ≤ 0,
a nikdy nemůže dojít k situaci, že by program zjišťoval prvek na pozici 0 nebo
menší v poli A.
Bublinkové třídění (BubbleSort) pracuje jinak než dva dříve popsané algoritmy. Algoritmu se říká „bublinkový“, protože podobně jako bublinky v limonádě „stoupají“ vysoká čísla v poli vzhůru. Postupně se porovnávají dvojice sousedních prvků, řekněme zleva doprava, a pokud v porovnávané dvojici následuje menší číslo po větším, tato dvě čísla se prohodí. Celý postup opakujeme, dokud probíhají nějaké výměny. Protože algoritmus skončí, když nedojde k žádné výměně, je pole na konci algoritmu setříděné.
procedure BubbleSort(var A: Pole);
var i, x: integer;
zmena: boolean;
begin
repeat
zmena:=false;
for i:=1 to N-1 do
if A[i] > A[i+1] then begin
x:=A[i]; A[i]:=A[i+1]; A[i+1]:=x;
zmena:=true;
end;
until not zmena;
end;
def BubbleSort(pole):
zmena=True
while zmena:
zmena=False
for j in range(0,len(pole)-1):
if pole[j]>pole[j+1]:
pole[j],pole[j+1]=pole[j+1],pole[j]
zmena=True
Správnost algoritmu nahlédneme tak, že si uvědomíme, že po i průchodech
cyklem repeat bude posledních i prvků obsahovat největších i prvků
setříděných od nejmenšího po největší (rozmyslete si, proč tomu tak je).
Popsaný algoritmus se tedy zastaví po nejvýše N průchodech a jeho celková
časová složitost v nejhorším případě je O(N2), neboť na každý průchod
spotřebuje čas O(N). Výhodou tohoto algoritmu oproti předchozím dvěma je, že
je tím rychlejší, čím blíže bylo zadané pole k setříděnému stavu – pokud bylo
úplně setříděné, tehdy algoritmus spotřebuje jen lineární čas O(N).
Rychlé metody
Sofistikovanější třídící algoritmy pracují v čase O(N log N). Jedním z nich je třídění sléváním (MergeSort), založené na principu slévání (spojování) již setříděných posloupností dohromady. Představme si, že již máme dvě setříděné posloupnosti a chceme je spojit dohromady. Jednoduše stačí porovnávat nejmenší prvky obou posloupností a menší z těchto prvků vždy odstranit a přesunout do nové posloupnosti. Je zřejmé, že ke slití dvou posloupností potřebujeme čas úměrný součtu jejich délek.
My si zde popíšeme a předvedeme modifikaci algoritmu MergeSort, která používá pomocné pole. Algoritmus lze implementovat při zachování časové složitosti i bez pomocného pole, ale je to o dost pracnější. Existuje též modifikace algoritmu, která má počet fází (viz dále) v nejhorším případě O(log N), ale pokud je již pole na začátku setříděné, proběhne pouze jediná a v takovém případě má algoritmus časovou složitost O(N). My si však zatajíme i tuto variantu.
Algoritmus pracuje v několika fázích. Na začátku první fáze tvoří každý prvek jednoprvkovou setříděnou posloupnost a obecně na začátku i-té fáze budou mít setříděné posloupnosti délky 2i-1. V i-té fázi tedy vždy ze dvou sousedních 2i-1-prvkových posloupností vytvoříme jedinou délky 2i. Pokud N není násobkem 2i, bude délka poslední posloupnosti zbytek po dělení N číslem 2i. Zastavíme se, pokud 2i≥ N, tj. po ⌈ log2 N⌉ fázích.
Protože v i-té fázi slijeme ⌈N/2i⌉ dvojic posloupností o nejvýše 2i-1 prvcích, je časová složitost jedné fáze O(N). Celková časová složitost popsaného algoritmu je O(N log N).
procedure MergeSort(var A: Pole);
var P: Pole; { pomocné pole }
delka: integer; { délka setříděných posl.}
i: integer; { index do vytvářené posl.}
i1, i2: integer; { index do slévaných posl.}
k1, k2: integer; { konce slévaných posl.}
begin
delka:=1;
while delka<N do begin
i1:=1; i2:=delka+1; i:=1;
k1:=delka; k2:=2*delka;
while i2<=N do begin
{ sléváme A[i1..k1] s A[i2..k2] }
if k2>N then k2:=N;
while (i1<=k1) or (i2<=k2) do
if (i2>k2)or((i1<=k1)and(A[i1]<=A[i2]))
then begin
P[i]:=A[i1]; i:=i+1; i1:=i1+1;
end
else begin
P[i]:=A[i2]; i:=i+1; i2:=i2+1;
end;
i1:=k2+1; i2:=i1+delka;
k1:=k2+delka; k2:=k2+2*delka;
end;
A:=P;
delka:=2*delka;
end;
end;
def MergeSort(pole):
pom=[0 for x in range(len(pole))]
delka=1 # delka aktualniho bloku
maxIndex=len(pole)-1 # nejvyssi index v seznamu
while delka<len(pole):
i=0; j=min(delka-1,maxIndex)
# prvni interval
i2=delka; j2=min(2*delka-1,maxIndex)
# druhy interval
indexVPom=0
# aktualni index v pomocnem seznamu
while i<len(pole):
# jeden pruchod=jedno sliti dvou bloku
while i<=j or i2<=j2:
if i2>j2 or (i<=j and pole[i]<pole[i2]):
pom[indexVPom]=pole[i]
indexVPom+=1
i+=1
else:
pom[indexVPom]=pole[i2]
indexVPom+=1
i2+=1
i+=delka # posun na nasledujici bloky
i2+=delka
j+=2*delka
j2+=2*delka
j=min(j,maxIndex)
# aby delka seznamu nebyla mocninou dvojky
j2=min(j2,maxIndex)
pole=list(pom) # zkopiruj seznam zpet
delka*=2
V čase O(N log N) pracuje také algoritmus jménem QuickSort. Tento algoritmus je založen na metodě Rozděl a panuj. Nejprve si zvolíme nějaké číslo, kterému budeme říkat pivot. Více si o jeho volbě povíme později. Poté pole přeuspořádáme a rozdělíme je na dvě části tak, že žádný prvek v první části nebude větší než pivot a žádný prvek v druhé části naopak menší. Prvky v obou částech pak setřídíme rekurzivním zavoláním téhož algoritmu. Je zřejmé, že po skončení algoritmu bude pole setříděné.
Malá zrada spočívá ve volbě pivota. Pro naše účely by se hodilo, aby levá i pravá část pole byly po přeházení přibližně stejně velké. Nejlepší volbou pivota by tedy byl medián tříděného úseku, tj. prvek takový, jenž by byl v setříděném poli přesně uprostřed. Přeuspořádání jistě zvládneme v lineárním čase, a pokud by pivoty na všech úrovních byly mediány, pak by počet úrovní rekurze byl O(log N). Protože je navíc na každé úrovni rekurze součet délek tříděných posloupností nejvýše N, bude celková časová složitost O(N log N).
Ačkoli existuje algoritmus, který medián pole nalezne v čase O(N), v QuickSortu se obvykle nepoužívá, jelikož konstanta u členu N je příliš velká v porovnání s pravděpodobností, že náhodná volba pivota algoritmus příliš zpomalí. Většinou se pivot volí náhodně z dosud nesetříděného úseku. Dá se ukázat, že takovýto algoritmus s velmi vysokou pravděpodobností poběží v čase O(N log N).
Důkaz tohoto tvrzení je trošičku trikový a lze jej nalézt např. v knize Kapitoly z diskrétní matematiky od pánů Matouška a Nešetřila. Je však třeba si pamatovat, že pokud se pivot volí náhodně, může rekurze dosáhnout hloubky N a časová složitost algoritmu až O(N2) – představme si, že se pivot v každém rekurzivním volání nešťastně zvolí jako největší prvek z tříděného úseku. V naší implementaci QuickSortu pro názornost nebudeme pivot volit náhodně, ale vždy jako pivot vybereme prostřední prvek tříděného úseku.
procedure QuickSort(var A: Pole; l, r: integer);
var i, j, k, x: integer;
begin
i:=l; j:=r;
k:=A[(i+j) div 2]; { volba pivota }
repeat
while A[i]<k do i:=i+1;
while A[j]>k do j:=j-1;
if i<=j then begin
x:=A[i]; A[i]:=A[j]; A[j]:=x;
i:=i+1;
j:=j-1;
end;
until i >= j;
if j>l then QuickSort(A, l, j);
if i<r then QuickSort(A, i, r);
end;
def QuickSort(pole,l,r):
i=l
j=r
k=pole[(l+r)//2] # pivot
while i<j:
while pole[i]<k: i+=1
while pole[j]>k: j-=1
if i<=j:
pole[i],pole[j]=pole[j],pole[i]
# prohozeni prvku
i+=1
j-=1
if l<j:
QuickSort(pole, l, j)
if i<r:
QuickSort(pole, i, r)
Metody pro specifická data
Ještě si předvedeme dva třídící algoritmy, které jsou vhodné, pokud tříděné objekty mají některé další speciální vlastnosti. Prvním z nich je třídění počítáním (CountSort). To lze použít, pokud tříděné objekty obsahují pouze klíče a možných hodnot klíčů je málo. Tehdy si stačí spočítat, kolikrát se který klíč vyskytuje, a místo třídění vytvořit celé pole znovu na základě toho, kolik jednotlivých objektů obsahovalo pole původní. My si tento algoritmus předvedeme na příkladu třídění pole celých čísel z intervalu ⟨D,H⟩:
const D = 1;
H = 10;
procedure CountSort(var A: Pole);
var C: array[D..H] of integer;
i, j, k: integer;
begin
for i:=D to H do C[i]:=0;
for i:=1 to N do C[A[i]]:=C[A[i]] + 1;
k:=1;
for i:=D to H do
for j:=1 to C[i] do begin
A[k]:=i;
k:=k+1;
end;
end;
D=1; H=10
def CountSort(pole):
vyskyty=[0 for x in range(D, H+1)]
for x in pole:
vyskyty[x-D]+=1
k=0
for i in range(D, H+1):
for j in range(vyskyty[i-D]):
pole[k]=i
k+=1
Časová složitost takovéhoto algoritmu je lineární v N, ale nesmíme zapomenout přičíst ještě velikost intervalu, ve kterém se prvky nacházejí (K=H-D+1), protože nějaký čas spotřebujeme i na inicializaci pole počítadel. Celkem tedy O(N + K).
Pokud by tříděné objekty obsahovaly vedle klíčů i nějaká data, můžeme je místo pouhého počítání rozdělovat do přihrádek podle hodnoty klíče a pak je z přihrádek vysbírat v rostoucím pořadí klíčů. Tomuto algoritmu se říká přihrádkové třídění (BucketSort) a my si popíšeme jeho víceprůchodovou variantu (RadixSort), která je vhodnější pro větší hodnoty K.
V první fázi si čísla rozdělíme do přihrádek (skupin) podle nejméně významné cifry a spojíme do jedné posloupnosti, v druhé fázi čísla roztřídíme podle druhé nejméně významné cifry a opět spojíme do jedné posloupnosti atd. Je důležité, aby se uvnitř každé přihrádky zachovalo pořadí čísel v posloupnosti na začátku fáze, tj. posloupnost uložená v každé přihrádce je vybranou podposloupností posloupnosti ze začátku fáze.
Tvrdíme, že na konci i-té fáze obsahuje výsledná posloupnost čísla utříděná podle i nejméně významných cifer. Zřejmě i-té nejméně významné cifry tvoří neklesající posloupnost, neboť podle nich jsme právě v této fázi rozdělovali čísla do přihrádek, a pokud dvě čísla mají tuto cifru stejnou, jsou uložena v pořadí dle jejich i-1 nejméně významných cifer, neboť v každé přihrádce jsme zachovali pořadí čísel z konce minulé fáze.
Na závěr poznamenejme, že místo čísel podle cifer lze do přihrádek rozdělovat též textové řetězce podle jejich znaků, atp.
Jak je to s časovou složitostí této varianty RadixSortu? Pokud třídíme celá čísla od 1 do K a v každém kroku je rozdělujeme do ℓ přihrádek, potřebujeme logℓ K průchodů (tolik je cifer v zápisu čísla K v ℓ-kové soustavě). Každý průchod spotřebuje čas O(N+ℓ), takže celý algoritmus běží v čase O((N+ℓ) logℓ K). To je O(N), pokud K a ℓ jsou konstanty. My si předvedeme implementaci algoritmu pro K=255 a ℓ=2 (čísla budeme rozhazovat do přihrádek podle bitů v jejich binárním zápisu).
const K=255;
procedure RadixSort(var A: Pole);
var P0, P1: Pole;
k1, k2: integer;
i: integer;
bit: integer;
begin
bit:=1;
while bit<=K do begin
k1:=0; k2:=0;
for i:=1 to N do
if (A[i] and bit)=0 then begin
k1:=k1+1; P0[k1]:=A[i];
end
else begin
k2:=k2+1; P1[k2]:=A[i];
end;
for i:=1 to k1 do A[i]:=P0[i];
for i:=1 to k2 do A[k1+i]:=P1[i];
bit:=bit * 2; { bitový posun o jedna vlevo }
end;
end;
K=255
def RadixSort(pole):
bit=1
while bit<=K:
P0=[] # aktuální bit je 0
P1=[] # aktuální bit je 1
for x in pole:
if bit&x:
P1.append(x)
else:
P0.append(x)
pole=P0+P1
bit*=2 # bitový posun o jedna doleva
Dolní mez na rychlost třídění
Na závěr našeho povídání o třídících algoritmech si ukážeme, že třídit obecné údaje, se kterými neumíme provádět nic jiného než je navzájem porovnávat, rychleji než v Θ(N log N) nejen nikdo neumí, ale ani umět nemůže. Libovolný třídící algoritmus založený na porovnávání a prohazování prvků totiž musí na některé vstupy vynaložit řádově alespoň N log N kroků. (RadixSort na první pohled tento výsledek porušuje, na druhý však už ne, když si uvědomíme, o jak speciální druh tříděných dat se jedná.)
 Třídící algoritmus v průběhu své činnosti nějak porovnává prvky a nějak je
přehazuje. Provedeme myšlenkový experiment. Pozměníme algoritmus tak, že
nejdříve bude pouze porovnávat, podle toho zjistí, jak jsou prvky v poli
uspořádány, a když už si je jistý správným pořadím, prvky najednou přehází. Tím
se algoritmus zpomalí nejvýše konstanta-krát. Také pro jednoduchost
předpokládejme, že všechny tříděné údaje jsou navzájem různé. Porovnávací
činnost algoritmu si pak můžeme popsat tzv. rozhodovacím stromem. Zde je
příklad rozhodovacího stromu pro tříprvkové pole:
Třídící algoritmus v průběhu své činnosti nějak porovnává prvky a nějak je
přehazuje. Provedeme myšlenkový experiment. Pozměníme algoritmus tak, že
nejdříve bude pouze porovnávat, podle toho zjistí, jak jsou prvky v poli
uspořádány, a když už si je jistý správným pořadím, prvky najednou přehází. Tím
se algoritmus zpomalí nejvýše konstanta-krát. Také pro jednoduchost
předpokládejme, že všechny tříděné údaje jsou navzájem různé. Porovnávací
činnost algoritmu si pak můžeme popsat tzv. rozhodovacím stromem. Zde je
příklad rozhodovacího stromu pro tříprvkové pole:
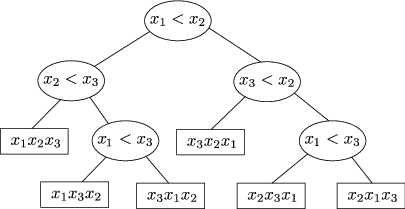
Každý vrchol obsahuje porovnání dvou prvků x a y, v levém podstromu daného vrcholu je činnost algoritmu, pokud x<y, v pravém podstromu činnost při x≥ y. V listech je už jisté správné pořadí prvků.
Každému algoritmu odpovídá nějaký rozhodovací strom a každý průběh činnosti algoritmu odpovídá průchodu rozhodovacím stromem od kořene do nějakého listu. Naším cílem bude ukázat, že v libovolném rozhodovacím stromu (a tedy i libovolném odpovídajícím algoritmu) bude existovat cesta z kořene do nějakého listu (neboli výpočet algoritmu) délky N log N.
Kolik maximálně hladin h, a tedy i jaká nejdelší cesta se v takovém stromu může vyskytnout? Náš strom má tolik listů, kolik je možných pořadí tříděných prvků, tedy právě N!. Různým pořadím totiž musí odpovídat různé listy, jinak by algoritmus netřídil (předpokládáme přeci, že to, jak má prvky prohazovat, může zjistit jenom jejich porovnáváním), a naopak každé pořadí prvků jednoznačně určuje cestu do příslušného listu. Na nulté hladině je jediný vrchol, na každé další hladině se oproti předchozí počet vrcholů nejvýše zdvojnásobí, takže na i-té hladině se nachází nejvýše 2i vrcholů. Proto je listů stromu nejvýše 2h (některé listy mohou být i výše, ale za každý takový určitě chybí jeden vrchol na h-té hladině). Z toho víme, že platí:
a proto:
Logaritmus faktoriálu se těžko počítá přesně, ale můžeme si ho zdola odhadnout pomocí následujícího pozorování:
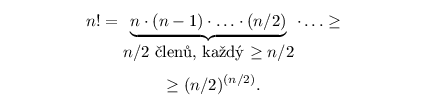
Dosazením získáme:

Vidíme tedy, že pro každý třídící algoritmus existuje vstup, na kterém se bude muset provést alespoň c·N log N kroků, kde c>0 je nějaká konstanta.
Poznámky
- Zkuste si též rozmyslet (drobnou modifikací předchozího důkazu), že ani průměrná časová složitost třídění nemůže být lepší než N log N.
 Odvodit průměrnou složitost QuickSortu vlastně není zase tak těžké.
Zkusme následující úvahu: Pokud by pivot nebyl přesně medián, ale alespoň se
nacházel v prostřední třetině setříděného úseku, byla by složitost stále
O(N log N), jen by se zvýšila konstanta v O-čku. Kdybychom pivota volili
náhodně, ale po rozdělení prvků si zkontrolovali, jestli pivot padl
do prostřední třetiny, a pokud ne (jeden z úseků by byl moc velký a druhý moc
malý), volbu bychom opakovali, v průměru by nás to stálo konstantní počet
pokusů (pokud čekáme na událost, která nastává náhodně s pravděpodobností p,
stojí nás to v průměru 1/p pokusů; zde je p=1/3), takže celková složitost
by v průměru vzrostla jen konstantně.
Odvodit průměrnou složitost QuickSortu vlastně není zase tak těžké.
Zkusme následující úvahu: Pokud by pivot nebyl přesně medián, ale alespoň se
nacházel v prostřední třetině setříděného úseku, byla by složitost stále
O(N log N), jen by se zvýšila konstanta v O-čku. Kdybychom pivota volili
náhodně, ale po rozdělení prvků si zkontrolovali, jestli pivot padl
do prostřední třetiny, a pokud ne (jeden z úseků by byl moc velký a druhý moc
malý), volbu bychom opakovali, v průměru by nás to stálo konstantní počet
pokusů (pokud čekáme na událost, která nastává náhodně s pravděpodobností p,
stojí nás to v průměru 1/p pokusů; zde je p=1/3), takže celková složitost
by v průměru vzrostla jen konstantně.
Původní QuickSort sice žádné takové opakování volby neprovádí a rovnou se zavolá rekurzivně na velký i malý úsek, ale opět se po v průměru konstantně mnoha iteracích velký úsek zredukuje na nejvýše 2/3 původní velikosti a třídění malých úseků jednotlivě nezabere víc času, než kdyby se třídily dohromady.
- Kdybychom u QuickSortu použili rekurzivní volání jen na menší interval, zatímco ten větší bychom obsloužili přenastavením proměnných a skokem na začátek právě prováděné procedury, zredukovali bychom paměťovou složitost na O(log N) (nepočítaje samotné pole čísel), jelikož každé další rekurzivní volání zpracovává alespoň dvakrát menší úsek než to předchozí. Časové složitosti tím však nepomůžeme.
- Počet přihrádek u RadixSortu vůbec nemusí být konstanta – pokud např. chcete třídit N čísel v rozsahu 1… Nk, stačí si zvolit ℓ=N a fází bude jenom k. Pro pevné k tak dosáhneme lineární časové složitosti.