Čtvrtá série dvacátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 20-4-1: Druidí nápisy
- 20-4-2: Stonehedge
- 20-4-3: Mince
- 20-4-4: Skupinky pro chytré
- 20-4-5: Roboti na útěku
- 20-4-6: Hrady, hrádky, hradla
20-4-1 Druidí nápisy (Zadání)
Tato úloha vám pravděpodobně přivodila značné bolesti hlavy, a proto došla všeho všudy dvě řešení. My si tedy budeme chvíli lámat hlavu společně, přičemž se pokusíme vyhnout zmíněným intelektuálním bolestem.
První úskok, kterého se dopustíme, bude odkaz na řešení úlohy 20-2-3. Jistě jste si povšimli, že zadání jsou si velmi podobná a vězte, že tak je tomu i u řešení. Proto se před dalším čtením ujistěte, že znáte zadání i řešení 20-2-3 a porozuměli jste dané problematice.
V tento moment můžeme předpokládat existenci několika částí našeho algoritmu a stavět na nich. Pro jistotu si však ještě shrňme nejdůležitěžší body, z nichž vyjdeme: k užitku přijde, že umíme vstupní slovník reprezentovat trií, kde navíc umíme pro každou posloupnost značek (značkami budeme rozumět např. tečky a čárky) okamžitě vypsat, jaká všechna slova může posloupnost kódovat; dalším stavebním kamenem bude postup, jakým jsme hledali nejkratší slovní reprezentaci řetězce – ten budeme upravovat pro naše potřeby a proto se na něho podíváme důkladněji.
Jak tedy vypadalo pole, které jsme pomocí dynamického programování naplnili, a co nám vlastně sdělovalo za informaci? Pole nám na indexu i pro každou podposloupnost vstupu od i do n (tedy jinak řečeno pro každý sufix vstupu začínající indexem i) poví, jaké slovo si máme vybrat jako první, aby výsledný rozklad vstupu na slova byl co nejkratší. To nás v důsledku odkazuje na další pozici v tomto poli atd…což už vedlo k řešení.
Nyní si představme, že naše pole B bude „chytřejší“ a poví nám více informací. Řekněme, že nám ke každému sufixu vstupu poví pro každé j, jestli je takovýto sufix rozložitelný na právě j slov. Takové pole je dvojrozměrné - B[i,j] = 1 pokud je sufix začínající na indexu i rozložitelný na j slov, v opačném případě je B[i,j] = 0. Konstrukce není nikterak složitá. Pro sufix nulové délky - tedy podposloupnost, která začíná za koncem řetězce a zároveň tam i končí - víme, že je rozložitelný pouze na 0 slov (B[n+1,0]=1 ale všechna ostatní B[n+1,1] = B[n+1,2] = … = B[n+1,n] = 0. Podobně jako v 20-2-3 budeme postupovat od nejkratšího sufixu až po nejdelší (celá posloupnost). Tedy pole B vyplňujeme od indexu n do indexu 1. Pro každý sufix snadno vyplníme hodnoty pro různá j, když známe všechna taková j kratších sufixů. Podrobněji prozkoumejme část, kdy jsme v druhé sérii vyplňovali položky pole na indexu i. Díky trii jsme nalézali jednotlivá slova, která mohou na daném indexu začínat a podle nich přepisovali údaj o nejkratším možném rozkladu. Zůstaňme u toho, že nacházíme jednotlivá slova od daného počátku i. Pak tedy víme, kde má začínat další slovo patřičného rozkladu (totiž hned za koncem prvního slova) – označme si takové místo indexem q (q = i + d, kde d je délka prvního slova a zřejmě tedy q > i]). Protože postupujeme od nejkratších sufixů, tj. pole vyplňujeme od konce, tak hodnoty na pozici q již známe). Nyní nám stačí podívat se, na kolik slov umíme rozložit sufix vstupu začínající indexem q. Jestliže lze sufix začínající v q rozložit na j slov, potom sufix začínající i lze rozložit na j + 1 slov. Tj. pokud B[q,j]=1 pak nastavíme B[i,j+1]=1. Zřejmě jen zkoušíme „dolepovat“ různá slova před začátek již existujících rozkladů – ačkoliv rozklady jako takové si nepamatujeme, pouze vedeme v patrnosti jejich existenci.
Tedy, právě jsme sestavili pole, podle kterého umíme říci, zda daný sufix lze rozložit na j slov. K čemu je nám to dobré? Umíme totiž nalézt všechny rozklady o daném počtu slov a vypsat je! Podívejme se na index 1, tedy na rozklad pro celý vstup. Vezměme si všechna j od nejmenšího k největšímu a uvažujme jen ta, pro která lze vstup rozložit na j slov (tedy B[1,j]=1). Pro každé takové j můžeme zkusit s pomocí trie dohledat různá slova, kterými může rozklad začínat. Každé takové slovo někde končí a rozklad pokračuje na pozici q bezprostředně za ním následující. My se na tato q podíváme a pokud pro sufix začínající od q existuje rozklad na j - 1 slov, pak si slovo, jenž nás posunulo na index q, můžeme do rozkladu vybrat. Zkráceně: Vyzkoušíme všechna slova, která mohou být na začátku, a podíváme se, jestli si je můžeme opravdu vybrat, tedy jestli za ně můžeme „dolepit“ rozklad pokračující j - 1 slovy (jednička se zřejmě odečítá za již zvolené slovo). Jak dál? Jsme na indexu q a chceme rozložit sufix od q na j - 1 slov. To už je ale ten samý problém, jako když jsme zkoušeli rozložit celý vstup na j slov. Pouze se liší místo, kde má rozklad začít, a počet slov, které má rozklad mít. Opět zkusíme všechna možná slova pro pokračování rozkladu a budeme se dívat, kam dál.
Jistě vás tedy napadá myšlenka použít rekurzi a de facto nasadit backtrack. My to opravdu uděláme, ale neděste se, ukážeme totiž, že to bude „slušný“ backtrack, který díky předpočteným informacím z části s dynamickým programováním (konstrukce dvojrozměrného pole) poběží rozumně rychle.
Backtrackující funkce potřebuje ke své činnosti znát počet již vypsaných rozkladů a stav právě zkoumaného rozkladu. Stav je charakterizován slovy, které jsme si již vybrali pro začátek rozkladu, indexem i, na kterém končí poslední z těchto slov, a konečně počtem slov j, které ještě do úplného rozložení zbývá. Funkce pak vyzkouší všechna slova, která by mohla na zadaném indexu začínat, a pokud pro nějaké z nich zjistí, že lze rozložit zbytek vstupu na j-1 slov (zkontroluje B[q,j-1]=1, kde q značí index těsně za kontrolovaným slovem), zavolá sama sebe. Tomuto synovskému volání přidá do rozkladu nalezené slovo a nový upravený stav – tedy index posunutý za konec takového slova a j snížené o 1. Pokud se po návratu ze synovského volání bude počet vypsaných rozkladů roven K, funkce svoji činnost ukončí. Tuto funkci spustíme postupně od nejkratšího na všechny rozklady začínající na indexu 1 – vyzkoušíme tak rozklady celého vstupu.
Podívejme se, jak dlouho trvá jedno volání našeho backtracku. Jsme na pevně zvoleném indexu a máme zadaný počet slov, na který máme vstup ještě dorozložit. Chceme přitom vypsat všechny možné rozklady dané délky. Projdeme až L indexů, kde může nějaké vybrané slovo končit (L označuje délku nejdelšího slova ve slovníku). Avšak pro každé slovo už vykonáme dotaz v konstantním čase do našeho zkonstruovaného pole. Pak už opět voláme sami sebe.
U backtracků obecně nám časovou složitost zhoršuje veliké množství větví výpočtu. Průběh výpočtu nějaké backtrackující funkce si totiž můžeme představovat jako strom, kde každý vrchol odpovídá jednotlivým voláním funkce, a hrany znázorňují vztah volající-volaný. Pokud se strom v každém vrcholu větví třeba jen dvakrát a hloubka stromu je řekněme 100, pak celková velikost stromu bude 2100. V našem případě vyzkoušíme až L indexů. Ještě poznamenejme, že určitě L ≤ n, protože kdyby tomu tak nebylo, museli bychom mít nějaké slovo delší než celý vstup. Takové slovo ale není k ničemu a můžeme ho zahodit. Mohlo by se zdát, že náš algoritmus poběží v čase O(nn), což se tváří dosti beznadějně.
Nyní si připomeňme, že nám stačí K nejkratších rozkladů, tedy můžeme backtrack po vypsání těchto rozkladů ukončit. Dalším důležitým postřehem je, že nikdy nevstoupíme do „slepých“ větví výpočtu – tedy nezkoušíme něco, co nevede k výsledku. To nám zajistilo právě dynamickým programováním zkonstruované pole B, kterého se tak v důsledku ptáme, zda máme vůbec nějaký rozklad zkoušet. Spojením těchto pozorování je fakt, že strom volání naší backtrackující funkce má právě K listů. Celková hloubka stromu je nejvýše n (připomeňme, že za n rozumíme délku vstupní posloupnosti) – úroveň v hloubce h odpovídá částečnému rozkladu s h slovy, ale protože každé slovo má alespoň jedno písmeno, nemůžeme nikdy ve stromu být hlouběji než v hloubce n. Tedy celkový počet volání backtrackující funkce je nejvýše K ·n. Pro každý list pak musíme ještě celý rozklad vypsat, což ale stíháme rovněž v K ·n. To už dává pro funkci rozumně vypadající časový odhad O(K ·n2), kde pro každé volání funkce zohledňujeme režiji O(n) na vyzkoušení slov.
Celková paměťová složitost programu je nejvíce zatížena použitým dvojrozměrným polem B, protože vše ostatní je lineárně velké vzhledem k délce vstupu, výsledkem je tedy O(n2). Časová složitost je ovlivněna konstrukcí trie v O(P), kde P označme celkovou velikost slovníku. Dále počítáme ono dvojrozměrné pole B – ke každému z n indexů vyzkoušíme až n dalších. Pro každý z těchto n indexů vykonáme až n přepisování údajů (vyplňování hodnot rozkladů). Tedy dynamický výpočet je v O(n3). Backtrack potom v O(K ·n2). Celkem tedy O((K ·n2 + n3 ).
 Zrychlujeme…Pozorní čtenáři si jistě všimli, že s časem poměrně
plýtváme a jistě lze úlohu vyřešit lépe. Konkrétně budeme zrychlovat backtrack.
Zrychlujeme…Pozorní čtenáři si jistě všimli, že s časem poměrně
plýtváme a jistě lze úlohu vyřešit lépe. Konkrétně budeme zrychlovat backtrack.
Podívejme se, zda nevykonáváme příliš mnoho kroků v každém z volání naší funkce. Zkoumáme totiž často až zbytečně mnoho indexů, jestli z nich nemůže náš rozklad pokračovat. Tedy ke každému i zkoušíme až n indexů. Kdyby se nám podařilo vyhnout se testování zbytečných indexů, znatelně si pomůžeme. Označmě q1, q2 … , qm všechny indexy, pro něž se náš výpočet větví a kterými pokračuje rozklad. Za zbytečné indexy pak budeme považovat ty, které leží za qm. Na první pohled se zdá, že si pranic nepomůžeme, ale opak je pravdou. Pohleďme na problém šalamounsky a „naúčtujme“ procházení indexů až do qm někomu jinému, v našem případě oním šťastlivcem bude výpis rozkladu.
Uveďme na příkladu: Ocitáme se právě uprostřed výpočtu. Řekněme, že náš rozklad má již h slov a nacházíme se na indexu 100. Ve slovníku je celkem W slov, ale pouze pro w znich existují rozklady od aktuálního indexu. Délka nejdelšího z těchto w slov je řekněme 42. Délka nejdelšího slova ve slovníku je třeba 123. Pak za zbytečné indexy pokládáme všechny od 143 dál (až do 223 = 100 + 123). Tedy B[143, 0 … m] … B[223, 0 … m] už nezkoušíme. Oněch prvních 42 znaků musíme vypsat tak jako tak, což znamená, že tyto kroky není nutné započítávat.
Pro každé z použitých q1, … qm budeme stejně muset vypsat celé slovo a proto můžeme s čistým svědomím všechny kroky potřebné k jejich určení započítávat do výpisu těchto slov (víceméně násobíme konstantou 2). Problematické jsou pouze zbytečné indexy, které nemáme komu naúčtovat, ale právě proto je vynecháme. Ve skutečnosti jsme tak schovali veškerou časovou režiji naší funkce do výpisu, o kterém ale víme, že spotřebuje O(K ·n).
Co k tomuto úskoku budeme potřebovat? Postačí nám, když budeme znát poslední index qm a to pro každou dvojici (index, počet slov rozkladu) – to znamená navíc ke každému B[i,j]. Pro rozklady o různém počtu slov se totiž q1, … qm obecně liší. Během výpočtu našeho dvojrozměrného pole B si budeme počítat i nějaké další pomocné pole Q[i,j]=qm. V backtracku postačí se dívat do tohoto pole a nezkoušet indexy za Q[i,j].
Snížili jsme odhad časové složitosti funkce na O(K ·n) a celkovým výsledkem je O(K ·n + n3).
Ještě poznámka na závěr: Náš algoritmus jsme se záměrně optimalizovali na paměťovou složitost nezávislou na K a to za cenu dynamického výpočtu v O(n3). Důvodem je možná velikost K. Představme si, že vstup bude pouze z teček a ve slovníku budou pouze dvě slova. Jejich zápisem bude jedna a dvě tečky. Počet možných rozkladů vstupu délky n pak bude Fn, kde Fn je n-té Fibonacciho číslo. Ty snadno odhadneme zdola na 2n/2, protože z Fn+2=Fn+1+Fn plyne, že Fn+2 je alespoň dvakrát větší než Fn. A exponenciální paměťovou složitost si opravdu dovolit nemůžeme.
20-4-2 Stonehedge (Zadání)
Napřed uděláme několik pozorování.
Z každého rohu vedou právě dvě úsečky. Méně nedává smysl a více dává křížení.
Jedna z těchto úseček bude vodorovná a jedna svislá (jinak by to nebyl roh, ale průchod bodem). Tedy, každý vrchol má svého vodorovného a svislého souseda.
Nyní si vezměme například vodorovné sousedy (pro svislé to bude obdobné). Vodorovný soused má stejnou y-ovou souřadnici.
Rozdělme si tedy všechny body do skupin podle y. Podívejme se na jednu takovou skupinku a setřiďme si ji, řekněme, odleva. Ten úplně vlevo musí mít svého souseda (a to v této skupince), ale jediný, který připadá v úvahu je ten nejbližší napravo od něj. Takže je spojíme. Tím jej samozřejmě použijeme (může mít jen jednoho souseda) a stejná situace tedy nastává se třetím a čtvrtým a tak dále.
Všimněme si, že v každé skupince musí být sudý počet vrcholů. Kdyby nebylo, tak to zřejmě není kámen popsaný v zadání (poslední nemá s čím sousedit).
Takto můžeme zpracovat všechny skupinky. A obdobným způsobem můžeme spárovat i svislé dvojice.
Jak to ale udělat rychle? Pokud si setřídíme body lexikograficky podle (y,x), pak budou vždy všechny body se stejnou y-ovou souřadnicí za sebou, seřazené dle x-ové. A protože mají skupinky sudé počty, můžeme takto setříděnou posloupnost prostě začít spojovat po dvojicích od začátku (a nestarat se, kde začíná jedna skupinka a druhá končí).
Nyní již máme ke každému bodu jeho svislého a vodorovného souseda (svislé sousedy uděláme stejně, jen setřídíme dle (x,y)). Musí tvořit uzavřený cyklus (neboť v kameni nejsou díry a všechny body musí být na kameni a obvod je jistě souvislý). Takže jej stačí jen vypsat a jediný problém je, kterým směrem začít.
Pokud si vybereme některý vrchol na „horní vrstvě“ a ten má svého pravého souseda, pak je to zajisté po směru hodinových ručiček. A nejlevější vrchol svého pravého souseda bude mít určitě. Mimochodem, tento vrchol skončil jako první při setřídění dle (y,x).
Jak rychle to dokáže běžet? Načtení zvládneme lineárně, výpis také (to jen procházíme kolem dokola, než narazíme opět na ten první). Rozdělení na dvojice jde také lineárně – každý bod zapojíme jednou vodorovně a jednou svisle. Jediný problém je tedy s tříděním, které (v obecném případě) nezvládneme rychleji, než v O(N· log N).
Paměťová složitost je lineární, stačí si pamatovat jednotlivé body a jejich sousedy.
20-4-3 Mince (Zadání)
Do zadání se nám vloudila jedna drobná nejednoznačnost. Není zřejmé, zda v případě, kdy jsou na počátku 4 mince lícem vzhůru trpaslík hned ukončí hru, či ne. Pokud tomu tak nebude, přidáme na začátek „tah“, kdy neotočíme žádnou minci a vše převedeme na první případ.
Nejprve si uvědomme, že všechny možnosti, jak jsou mince otočeny (nazveme toto stavem mincí), je možno rozdělit na šest skupin (matematicky se mluví o kongruenci), které se při otočení nemění (tj. pokud vezmeme stav z nějaké skupiny a otočíme soudek, bude stav patřit do té samé skupiny). Popišme je vzájemnou polohou a počtem mincí, které jsou lícem vzhůru. To mohou být všechny (a tedy končíme), tři mince, dvě mince úhlopříčně, dvě mince vedle sebe, jedna mince, nebo žádná. Pokud tedy zjistíme, kterou skupinu převádí daný tah (tj. otočení mincí) na kterou, můžeme najít jejich posloupnosti, které každou z pozic převedou na první z nich a tím jsme hotovi.
Jak na to? Pro zjednodušení uvažujme, že každý lichý tah otočíme na soudku všechny mince a navrhujeme jen sudé. Ten nám převádí skupinu se čtyřmi a žádnou mincí lícem nahoru mezi sebou. Stejně tak mezi sebou přechází trojice, resp. samotná mince. Zbylých dvou skuipn, odpovídajících dvěma mincím lícem vzhůru, se tento tah nedotkne. Slučme tedy příslušně skupiny mezi sebou a označme si je jako (4) v případě, že jsou všechny mince stejnou stranou vzhůru, (2U) když jsou dvě mince úhlopříčně lícem vzhůru a dvě ne, (2V) případ, kdy jsou dvě mince vedle sebe lícem vzhůru a dvě ne a (1) stavy, je jedna mince nějak otočena a zbylé tři opačně.
Další užitečné pozorování je, že při otočení sudého počtu mincí se nezmění parita počtu mincí lícem vzhůru (tj. pokud byl lícem vzhůru lichý počet mincí, zůstane lichý, a pokud sudý zůstane sudý). Tedy otočením sudého počtu mincí převedeme stav ze skupiny (1) na stav ze skupiny (1) a stavy skupin ((4),(2U),(2V)) na stavy z té samé trojice skupin. Pokud otočíme jednu (nebo libovolný lichý počet mincí), převede to (1) na stav z některé ze skupin ((4),(2U),(2V)) (do které skupiny přesně se dostaneme záleží na otočení soudku a kterou přesně minci bereme) a stavy ze skupin ((4),(2U),(2V)) na stavy skupiny (1). Pokusme se tedy najít posloupnost otáčení sudého počtu mincí, kterou jsme schopni dostat stavy ze „sudých“ skupin ((4),(2U),(2V)) dostat na (4). Pokud nám nevyřeší problém, tak musel stav patřit (a stále patří) do skupiny (1). Otočením jedné mince ho převedeme na nějaký stav ze „sudých“ skupin a, jelikož už víme, že stav ze skupiny (1) nemůžeme mít, stejnou posloupností tahů trpaslíka porazíme.
Zbývá tedy podívat se na to, jak vyřešit skupiny (4), (2U) a (2V). Uvažujme pro tento odstavec, že víme, že lícem nahoru byl sudý počet mincí. (4) ani řešit nemusíme - tu nám zastaví trpaslík. (2U) je jednoduché - otočením dvojice mincí úhlopříčně na soudku dostaneme (4) (a tedy trpaslík nás zastaví) a z (2V) se nám stane (2V). Po „prvním“ tahu, pokud nás trpaslík nezastavil, víme, že stav soudku je ze skupiny (2V). Jako „druhý“ tah otočíme dvojici mincí vedle sebe. Podle toho, jak byl zrovna natočen soudek, dostaneme stav ze skupiny (4) nebo (2U). Pokud nás stále trpaslík nezastavil, patří do skupiny (2U) a tedy po otočení dvojíce mincí úhlopříčně budou všechny rubem (nebo lícem) vzhůru.
Tím jsme tedy nastínili, jak získat vyhrávající strategii. Konkrétně bude vypadat:
otoč všechny 4 mince
otoč 2 mince úhlopříčně
otoč všechny 4 mince
otoč 2 mince vedle sebe
otoč všechny 4 mince
otoč 2 mince úhlopříčně
otoč všechny 4 mince
otoč jednu minci
otoč všechny 4 mince
otoč 2 mince úhlopříčně
otoč všechny 4 mince
otoč 2 mince vedle sebe
otoč všechny 4 mince
otoč 2 mince úhlopříčně
otoč všechny 4 mince
Malá poznámka na závěr. Rychlejší strategie, než zde uvedené ani neexistuje. Pro začátek uvažujme, že máme jen zavázané oči (a nevíme, jaké je počáteční otočení mincí), ale trpaslík netočí se soudkem. Uvažujme všechny přípustné stavu soudku (tj. takové, kdy nám trpaslík ještě nezastavil hru). Každým tahem můžeme maximálně jednu z těchto pozic převést na tu, kdy jsou všechny lícem vzhůru a tím jí vyloučit (buď nás trpaslík zastaví, nebo to tenhle stav mincí nebyl). Zbylé pozice se nám vzájemně jednoznačně převedou na (možná) jiné stavy. Vzájemně jednoznačně znamená, že po provedení tahu budeme schopni určit jaká byla původní pozice (např. provedením toho samého tahu podruhé se vrátíme zpět) a tedy i že počet různých přípustných pozic se nám nezmenší, resp. zmenší o jednu, kterou jsme vyloučili. Jelikož na začátku máme jeden z 15-ti stavů a nevíme který, potřebujeme alespoň 15 tahů abychom libovolný z nich otočili lícem vzhůru. Pokud trpaslík „začne“ točit soudkem, určitě strategie řešící tuhle úlohu nebude kratší než v případě, kdy neotáčí. A protože nalezená strategie 15 tahů má, musí být nejkratší možná.
20-4-4 Skupinky pro chytré (Zadání)
Operace nad skupinkami přesně odpovídají operacím nad haldou z kuchařky 4. série, a naše rešení bude opravdu vycházet z haldy. Protože nechceme hledat jedince s minimálním IQ (těch je dost :-), ale s maximálním, bude zapotřebí otočit porovnávání.
Větší rozdíl spočívá v tom, že operace potřebujeme provádět "nedestruktivně" – nesmíme měnit již existující skupinky. Na principu fungování haldy se nic nemění, ale data nebudeme moci ukládat do pole jako v kuchařce. Strom uložíme jako sadu prvků (struct Node) pospojovaných pointery na levého a pravého syna. Operace nad haldou tak bude jednoduché dělat nedestruktivně: místo modifikace prvku naalokujeme nový prvek, zkopírujeme hodnoty ze starého prvku, a upravíme co je potřeba upravit. Při modifikaci syna budeme muset vždy vyrobit i nového otce a dál až ke kořeni.
Pro haldové operace potřebujeme efektivně umět pracovat s nejpravějším prvkem ve spodní hladině, a potřebujeme umět určit otce daného prvku. V poli je situace jednoduchá, požadovaný prvek je v poli tolikátý, kolik je prvků v haldě, a otec je na pozici i/2 (kde i je pozice syna).
Jednoduché řešení by bylo přidat do každého prvku ukazatel na jeho otce, a držet si ukazatel na nejpravější prvek ve spodní hladině; ale toto řešení použít nemůžeme, protože ukazatel na otce by nám neumožnil pracovat "nedestruktivně".
Naštěstí je možné i-tý prvek najít pomocí bitového zápisu i, stačí postupovat od kořene a dle hodnoty bitu jít do levého nebo pravého podstromu. Pokud si do pomocného pole schováme prvky, které jsme prošli, odpadne též problém s hledáním předchůdců.
Časová složitost operací insert a delete_best je
O(log(n)), časová
složitost find_best je O(1). Operace find_best nepotřebuje žádnou dodatečnou
paměť, insert i delete_best naalokují O(log(n)).
(S diky Petru Ondrúškovi.)
20-4-5 Roboti na útěku (Zadání)
Řešitele této úložky lze rozdělit do dvou skupin. Skupina první (která měla mohutnost pouze 3) přišla, viděla a s přehledem vyřešila. Skupina druhá (značně početnější) přišla, viděla, nevěřila svým očím, a tak raději vůbec neřešila. Pojďme se nyní podívat, jak si s roboty poradit …
K řešení našeho problému použijeme procházení stavového prostoru do šířky. U všech procházení je nejtěžší poznat, jak vypadá zmíněný stavový prostor. Obecně je stavový prostor orientovaný graf, kde vrcholy představují jednotlivé stavy a hrany přechody mezi nimi (jednotlivé kroky). V našem případě je stav definován polohou obou robotů a všech stráží. Z každého stavu pak vedou nejvýše čtyři hrany – jedna pro každý potencionální příkaz, který mohou roboti obdržet (stráže se pohybují automaticky, takže není potřeba jejich pohyb dále řešit). Některé hrany (případně i stavy) mohou být z prostoru vyloučeny, protože v nich dojde k zajmutí některého z robotů.
Bohužel nemůžeme stavy reprezentovat přímočaře, jak bylo popsáno. Pejsek je zakopaný v počtu stráží. Kdyby jich v obou bludištích byl maximální počet (tedy 10), potřebovali bychom vhodně ukládat informace o (x1y1x2y2)11 stavech. Naštěstí víme, že stráže neustále chodí po stejných trasách a délka jejich tras může být pouze 2, 3 nebo 4. Podle toho se pozice stráže opakuje vždy po 2, 4 nebo 6 krocích. Nejmenší společný násobek těchto čísel je 12, takže každých 12 kroků se pozice všech stráží opakuje. Pokud víme, ve které z 12-ti možných pozic se právě stráže nachází, jsme schopni spočítat její polohu jen ze vstupních dat.
Jak již bylo naznačeno, prostor budeme prohledávat do šířky. Pro každý stav si potřebujeme pamatovat informaci, zda jsme v něm už byli, a také z jakého stavu jsme se do něho dostali, abychom pak mohli zrekonstruovat výslednou cestu. Maximální počet stavů bude 12 ×(20 ×20)2, protože existuje 12 možných pozic stráží a maximální rozměry bludiště jsou 20 ×20, celkem tedy 2 560 000 stavů. Stav dokážeme bez problému zakódovat do 32-bitového integeru, takže celkem spotřebujeme necelých 10 MB paměti na stavy a nejvýš tři čtvrtiny této hodnoty na frontu. S těmito čísly už se do CodExu vejdeme.
Samotný algoritmus pak přesně odpovídá tomu, co již známe z kuchařky. Na počátku vložíme do fronty výchozí stav a označíme jej za použitý. V každém kroku vybereme jeden stav z fronty, spočítáme všechny stavy, do kterých se z něj dá dostat, ty si označíme a vložíme do fronty. Algoritmus končí v okamžiku, kdy narazíme na stav, ve kterém jsou oba roboti venku z bludiště.
Výslednou cestu pak zrekonstruujeme tak, že postupujeme od koncového stavu zpět k výchozímu podle informací, které jsme si ke stavům uložili. Jediný zádrhel spočívá v tom, že cestu musíme vypsat v opačném pořadí, takže si ji musíme nejprve uložit a pak teprve vypsat.
Voila. Nyní už je dochutíme podle libosti a servírujeme kompilátoru.
20-4-6 Hrady, hrádky, hradla (Zadání)
a) První podúloha, tedy nalezení „křižítka“, bude snadná. Budou nám totiž stačit tři hradla XOR:
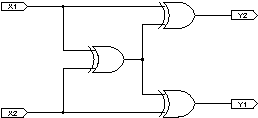
Proč tento obvod dělá to, co potřebujeme? Pokud jsou oba vstupy stejné, odpoví prostřední hradlo nulou, takže krajní hradla jen zkopírují vstup na výstup, což je správně. Pokud jsou naopak vstupy různé, prostřední hradlo odpoví jedničkou, takže krajní hradla vstup negují, a to je opět správně.
Dokázat bychom to mohli i algebraicky (⊕ je XOR):
A jak se dá na něco takového přijít? Zkusme uvažovat takto: Máme najít obvod se vstupy X1 a X2 a výstupy Y1 a Y2, který bude vždy počítat Y1=X1 a Y2=X2. Navíc tento obvod má být rovinný a pokud ho vepíšeme do kružnice, mají vstupy a výstupy po obvodu této kružnice dávat pořadí X1, X2, Y1, Y2. Jistě můžeme předpokládat, že hradlo, ze kterého vystupuje Y2, leží přímo na kružnici, takže do něj můžeme podél kružnice přivést vstup X1. Analogicky hradlo pro Y1 může znát Y2. Jak tedy spočítáme z X1 hodnotu Y2=X2? K tomu je potřeba informace o tom, zda se X1 a X2 liší či nikoliv. Tu lze snadno počítat uvnitř kružnice. A naše konstrukce je na světě.
Mimochodem, vystačili bychom si i s hradly NAND: Vzpomeňte si na konstrukci hradla xor ze čtyř NANDů – byla rovinná. Můžeme ji tedy dosadit do našeho schématu a získat křížící obvod z NANDů.
b) Druhá podúloha je zdánlivě dočista triviální. Pokud nějaký obvod není rovinný, je to proto, že se v něm vodiče kříží. Tak křížení nahradíme naším křižítkem a získáme obvod, v němž je o jedno křížení méně. To nám stačí provést konečně-krát a obvod bude rovinný. Jenže …
1. V jednom místě grafu by se mohlo křížit i více hran. Pokud se to stane, určitě existuje nějaké malé okolí tohoto bodu, kde nejsou žádná hradla ani další křížení. Tak všechny hrany, které se křížily, „rozšoupneme“ do tohoto okolí a z násobného křížení tím vyrobíme několik obyčejných.
2. Kdybychom křižítko umístili nešikovně, mohli bychom vyrobit nová křížení a celý proces zroviňování by se nikdy nezastavil. Pomůžeme si podobně jako od násobných křížení: najdeme dostatečně malou kružnici okolo místa křížení, kde se vyskytují jenom ty vodiče, které se křížení účastní (taková určitě existuje), a obvod vlepíme do ní. Víme přeci, že se do kružnice dá vepsat a jistě ho můžeme „ohnout“ tak, aby měl vývody na správných místech.
3. Mohli bychom v obvodu vytvořit cyklus – třeba tehdy, když se kříží vodič vedoucí na vstup nějakého hradla s vodičem vedoucím z výstupu téhož hradla. Cykly jsme sice v definici hradel v první sérii výslovně nezakázali (a jeden z ukázkových obrázků dokonce cyklus obsahuje), ale není nijak jasné, jak se takové obvody chovají. Teprve v páté sérii se něco takového pokoušíme zavést. Proto cykly v obvodech, kde dříve nebyly, při zroviňování nechceme vytvářet.
To se zařídí snadno: nakreslíme si schéma tak, aby bylo topologicky setříděné podle x-ové souřadnice. Na přímce x=0 budou ležet ta hradla, která závisí pouze na vstupech obvodu; poskládáme je tam libovolně. Na přímku x=1 umístíme ta, která závisí na vstupech obvodu a na výstupech již umístěných hradel, a tak dále. Pokud v obvodu není cyklus, postupně takto umístíme všechna hradla. Všimněte si, že nyní jsou v každém křížení oba vodiče naprosto nezávislé – hodnota na jednom nijak nezávisí na tom, jaká hodnota putuje druhým. Přidáváním křižítek tedy už nemohou cykly vznikat.