Třetí série dvacátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Zadání úloh
Třetí série dvacátého ročníku KSP
„Á, konečně jsem to našel,“ zvolal mág nadšeně a vítězoslavně pozvedl knihu nad hlavu.
„Tady se píše, že se musíme vydat směrem k Lávové hoře.“
Mág položil knihu na stůl a už se chystal provést složité kopírovací kouzlo, když se do věci vložil Felix:
„Tak to vám tedy opravdu nezávidím. To budete mít docela štreku.“
„Kráá?“ ozval se nechápavě Kiri.
„Hm, na tom něco bude. Lávová hora není zrovna za rohem a létat na koštěti,
to už na mě není. Průvan mi nedělá dobře na klouby.“
„No vidíte! Já říkal hned, že jsme měli zůstat doma,“ pochvaloval si kocour náhlou změnu plánu.
Mág mu ale hbitě zkazil náladu:
„Vildo, zajdeš na trh a pořídíš koně. Já tu zatím zkopíruji tu knihu, ať můžeme vyrazit ještě dnes!“
Vilda zašel k místnímu handlíři. Mezi dveřmi mu kývl na pozdrav a hned přešel k věci:
„Rád bych si pořídil jednoho koně. Nemusí jezdit moc rychle, ale musí vydržet dlouhou cestu.
Jo, a taky aby se neplašil, pokud uvidí něco neobvyklého.“
Handlíř vypadal velmi vyděšeně při pohledu na nazelenalého zákazníka.
Byl by vzal nohy na ramena, ale z jedné strany mu v tom bránila zeď a mezi dveřmi stál Vilda.
„T-t-třeba t-t-tohohle?“ zakoktal handlíř, když se mu vrátila řeč a ukázal přitom prstem na krásného bělouše.
„A v černé by nebyl?“
„B-bílý táhne první. To je výhoda, ne?“ vyblekotal handlíř první argument, který mu přišel na mysl.
V tu chvíli si ale Vildy všiml i bělouš, vzepjal se na zadní a málem tak převrhl koryto s vodou.
„Máte pravdu, tento není ten pravý,“ změnil handlíř názor.
Ale jak se ukázalo, žádný z přítomných koní nebyl dostatečně klidný, aby snesl pohled na Vildu.
„Možná bych to mohl ještě stihnout, než…“ zamumlal si handlíř pod vousy a zmizel v přilehlém uzenářství.
Za chvíli se vrátil a táhl za sebou něco, co budeme z nedostatku lepší terminologie nazývat koněm.
Kůň nevypadal, že by snesl cestu třeba jen za město, ale Vildův vzhled mu zřejmě nevadil.
Dokonce se mu přiblížil natolik, že mu dokázal vytáhnout z kapsy svačinu.
„Ale vždyť je slepý na jedno oko!“ všiml si Vilda.
„Ano. A ani za to nebudu chtít příplatek.“
„Prosím?“
„Když uvidíte něco opravdu neobvyklého, prostě okolo toho projdete zleva.“
Netrvalo dlouho a obchod byl uzavřen. Ale když došlo k placení, nastal problém.
Cena nepředstavovala žádné potíže, na té se shodli k oboustranné spokojenosti.
Zato se ukázalo, že vybrat správné mince je těžký úkol.
20-3-1 Platba koně (12 bodů)
Je zadán obnos peněz P, požadovaný za koně, a dvě hromádky mincí (jedna Vildova a jedna handlířova).
V každé hromádce mincí jsou mince různých hodnot a od každé hodnoty může být více mincí. Na Vildově
hromádce je celkem N mincí, na handlířově M.
Každá hodnota je desetinné číslo s přesností na 2 desetinná místa.
Vaším úkolem je nalézt způsob, jak zaplatit přesně P na co nejmenší počet vyměněných mincí, nebo zjistit, že to provést nelze.
Pozn: Hodnoty mincí nemusí tvořit žádný systém běžných platidel ani být jinak „rozumné“.
Příklad: Pro P=15,00, Vildovu hromádku obsahující dvě mince o hodnotách 20,00 a 45,73 a
handlířovu hromádku s mincemi o hodnotách 5,00 a 15,00 je správné řešení takové, že Vilda použije minci o hodnotě 20 a handlíř mu vrátí 5.
Pro P=16,16 a stejné hromádky mincí řešení neexistuje.
Řešení
Naložili koně, mág se nechal vysadit do sedla a vyrazili na cestu.
Cestovali dva dny, když se v křoví vedle cesty ozvaly hlasy.
Družinka se zastavila a všichni pozorně naslouchali.
„Dneska byl nějaký nesdílný. Asi mi už nevěří,“ stěžoval si první hlas.
„Taky? Prý máme přepadat u severní cesty. Ale číslo stromu mi neřekl.
Za prvním se nedá schovat, ale od druhého až k devadesát devátému je to stále ještě hrozně moc možností,“ rozumoval někdo další.
První si přisadil: „Hm, mně řekl jen součet čísel stromů.“
„Mně součin. Ale to mi moc nepomůže, z toho se nedají určit,“ kňoural druhý.
„I z toho součtu mi bylo hned jasné, že součin nikomu k ničemu nebude,“ souhlasil první.
„To ti z toho bylo jasné? Tak to já už vím, která čísla to jsou! Jdu si pro luk,“ zajásal druhý.
„Vážně? Tak v tom případě to vím také, kam jen jsem dal meč?“ pookřál první.
Mág sesedl z koně a celá družinka se ukryla za nedalekým kamenem. Sotva se jim
podařilo přimět koně, aby si lehl, vyskočili lupiči na cestu.
„Už odešli. Tak bychom mohli jít také,“ prohlásil Felix, kterému se celá záležitost vůbec nelíbila.
„Ano, ale potřebujeme jít okolo nich,“ zaškaredil se Vilda.
„Vildo, ty jsi nezabalil čaj!“ postěžoval si mág, když se prohraboval sedlovou brašnou.
„No, co se dá dělat. Vypadá to, že je budu muset proměnit v ježky.“
„Stejně tak, jako všechno ostatní, co se u každého stromu jen pohne?“ neodpustil si rýpnutí Felix.
Kiri při představě proměny zděšeně opustil strom, na kterém seděl, a s mírným žuchnutím přistál vedle koně.
„No tak ježků je tu stejně málo, tak by to tak moc nevadilo.
Ale alespoň bych si ušetřil práci, kdybych věděl, za kterými stromy jsou…“
20-3-2 Dva lupiči (8 bodů)
Úkolem této úlohy je najít všechny možné dvojice stromů, za kterými mají lupiči čekat.
Nestačí řešení pouze najít, je třeba také zdůvodnit, proč je správné a proč žádné další dvojice neexistují.
Pozn: předpokládejme, že lupiči jsou dokonalí matematici (mají cvik v počítání lupu) a
jsou z takových informací opravdu schopni zjistit svá čísla stromů v podstatě okamžitě.
Tedy prohlášení: „Tak to já už vím, která čísla to jsou,“ není myšleno ironicky,
ale opravdu znamená, že z dostupných informací dokáže odvodit ona čísla.
Pro případ, že by vám nějaké drobnosti utekly, uvedeme zde všechny informace ještě jednou:
Velitel lupičů si myslí dvě celá čísla mezi 2 a 99. Lupiči A prozradí jejich součin,
lupiči B prozradí jejich součet. Navíc A ví, že B zná součet, jen neví, kolik to je (a naopak).
Rozhovor pak probíhá následovně:
A: „Nevím, jaká čísla si myslí náš velitel.“
B: „Věděl jsem, že to nebudeš vědět.“
A: „Opravdu? V tom případě už vím, co je to za čísla.“
B: „V tom případě to vím taky.“
Řešení
Felix opovržlivě přičichl ke zlatě, které vyplašení ježci nechali za sebou při zoufalém úprku.
Ani tolik spěchat nemuseli, mezi našimi hrdiny nebyl nikdo ochotný běhat a mág prohlásil,
že bodliny na zádech jako jejich trest zcela stačí.
„Tak to bychom měli,“ pochvaloval si mág potěšen, že se mu tak složité kouzlo podařilo.
„A dej si patentovat tenhle způsob výroby ostnatého drátu,“ navrhl Felix,
který si při pozorování zlata všiml žížaly, která se nemohla zahrabat, protože měla po celém těle bodliny.
„Tomu se říká aktivní obranný systém. Teď ji alespoň nesezobne kos,“ vysvětlil mág a začal listovat v knize.
„Utáboříme se tu na noc,“ dodal po chvíli čtení.
Vilda rozdělal oheň, vybalil deky a uvařil večeři. Noc uběhla rychle a až
na vzdálené dupání ježků nic nerušilo mírumilovné ticho. Vildu ráno probralo
sluníčko a rosa.
„Vaše Mágstvo, kam pokračujeme dál?“ zeptal se Vilda, sotva si protřel oči.
Podíval se na mága a znejistěl: „Vždyť vypadáte jako kdybyste celou noc nespal!“
A opravdu. Mág měl červené oči, které držel sotva otevřené. Seděl u ohniště a
okolo sebe měl rozloženou hromadu papírů popsanou divnými symboly.
„Uáááh, cožeto?“ zívl ospalý mág. „Aha, cesta. To je právě ten problém.
Tady v knize sice píšou, že musíme najít Svítící bažinu. Ale celé je to popsané
těmi starodávnými hádankami, takže nemám ponětí, kam dál.“
Hádanka Vildovi tak tajemná nepřipadala. Stálo v ní: „Cesta nejdelší –
stále z kopce, jen osmkrát vykročit nahoru. A na konci cesty té, stoč se vpravo k obzoru.“
„A já nevím, jak takovou nejdelší cestu, co vede stále z kopce,
jen osmkrát kousek do kopce, najít. A věštění nepomohlo,“ postěžoval si smutně mág.
„To se divím. Posledně se ty vosy vykouřit podařilo,“ ohodnotil jeho věštecké schopnosti Felix.
Kiri se probudil a slétl z větve, na které spal. Dopadl doprostřed papírů a
vytvořil v nich malý kráter. Zoufale krákal a máchal křídly, aby se z té hromady
dostal. Vzduch se naplnil poletujícími papíry a havraním peřím.
Vilda se natáhl, aby havrana vytáhl, když v tom mu přímo na nose přistál papír
s nějakými čísly. Byly na něm vypsané výšky jednotlivých bodů na cestě.
„Ale vždyť stačí vybrat nejdelší takovou posloupnost čísel na tomhle papíru,“
zaradoval se a začal počítat.
„Kdybych nebyl tak ospalý, tak bych na to přišel sám…“ zamumlal mág,
když usínal.
20-3-3 Cesta z kopce (8 bodů)
Je zadána posloupnost A obsahující N čísel a nějaké číslo k.
Úkolem je nalézt indexy a, b (a ≤ b) takové, že b-a je největší možné a
posloupnost Aa, … , Ab obsahuje maximálně k dvojic těsně po sobě
jdoucích prvků Ai, Ai+1 takových, že Ai < Ai+1. Pro všechny
ostatní dvojice platí Ai ≥ Ai+1. Tedy až na k míst je posloupnost nerostoucí.
Příklad: Pro k = 1 a posloupnost 9, 7, 6, 4, 8, 6, 3, 9, 1 je správným výsledkem a = 1 a b = 7,
tj. podposloupnost 9, 7, 6, 4, 8, 6, 3.
Řešení
„Tady to vypadá strašidelně,“ postěžoval si Vilda, když se blížili k bažině.
„Samá voda. Alespoň nějaká lávka, kdyby tu byla,“ remcal Felix.
„Lávka tu sice není, ale jsou tu provazové mosty. A kolik,“ pochvaloval si mág.
A opravdu. Mezi stromy vedly stovky provazových mostů. Mág ze své kopie knihy
vytáhl mapu Svítící bažiny a s pomocí ostatních se vydrápal na nejbližší most.
Procházeli bažinou křížem krážem, od jednoho stromu k druhému.
Felix několikrát navrhl, že na ně počká na té či oné křižovatce, než se na ni zase vrátí.
„Rozhled na rašelinu bude z tamté křižovatky sice nádherný, ale klidně si ho nechám ujít.“
Když i mágovi došla trpělivost a konstatoval unaveně:
„Ta mapa je špatně. Tady už jsme byli nejméně šestnáctkrát a na tamté křižovatce třináctkrát. Bloudíme mezi nimi stále tam a zpět.
Mezi támhletou zatracenou křižovatkou a tímhle prokletým ztrouchnivělým stromem vede určitě nejvíce cest v celé bažině.
Ale nemůžu je najít na mapě.“
„To bude tím, že ta mapa je pěkně stará. Provazové mosty zůstaly natažené
mezi stejnými stromy, ale tohle je bažina a ty stromy v ní nedrží. Prostě se
od té doby přemístily,“ mudroval Vilda a strčil do nejbližšího stromu.
Strom se posunul o dobrý metr.
„V tom případě stačí zjistit, mezi kterými vede nejvíce různých cest.
Z toho pak dokážu zorientovat mapu…“
20-3-4 Orientace na mapě (10 bodů)
Na vstupu váš program dostane popis orientovaného grafu znázorňujícího mapu. Víte, že tento graf neobsahuje žádný
orientovaný cyklus, čili že neexistuje žádná orientovaná cesta délky alespoň 1, která by začínala a končila ve stejném vrcholu.
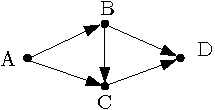
Úkolem programu je vypsat dvojici vrcholů, mezi kterými vede nejvíce různých cest v celém grafu.
Za různé jsou považovány libovolné dvě cesty, které se liší alespoň jednou hranou.
Pokud je takových dvojic vrcholů více, stačí libovolná z nich.
Příklad: Pro tento graf je řešením dvojice vrcholů A a D:
Řešení

Konečně vylezli z bažiny na správnou stranu. Zajásali, rozvázali nebohého koně a
mág z něho sňal levitační kouzlo.
Vyškrábali se na nejbližší kopec a rozhlédli se po okolí. V dálce spatřili
dýmající horu zahalenou v temných mracích. Lávová hora byla konečně na dohled…
20-3-5 Asfaltování (11 bodů)
Milí řešitelé a řešitelky,

blíží se zima a CodEx už se těší na vaše dárečky k Vánocům v podobě řešení úlohy
třetí série. Způsob odevzdávání a všechny ostatní detaily zůstávají stejné, jako
v minulých sériích. Takže pokud jste zapomněli, jak to v praktické úložce chodí,
nebo jste se do řešení KSP zapojili teprve teď, podívejte se na úložku 20-1-5
z první série, kde naleznete potřebné informace.
Zadání:
Obyvatelé Hipopotámie si již dlouho stěžovali na nekvalitní silnice. Když si
jednou i vrchní cestář při cestě do práce v kočáře vyrazil zub, rozhodl se
k radikální akci. Doslechl se, že v sousední zemi začali na cesty používat
novinku zvanou asfalt, a myšlenka na vyasfaltování všech silnic v Hipopotámii
byla na světě. A jak si vrchní cestář usmyslel, tak se i stalo. Při realizaci
nápadu se ale nižší cestáři museli potýkat s nemilým problémem: asfalt se
dovážel ze sousední země v ohromných barelech, ve kterých bylo asfaltu tak
akorát na dvě cesty (byly to opravdu ohromné barely). Potíž byla v tom, že
jakmile se barel narazil a asfalt z něj začal vytékat, nedal se už proud asfaltu
ničím zastavit a bylo tedy nutné vyasfaltovat najednou dvě na sebe navazující
cesty. Jenže jak rozvrhnout asfaltování, aby cestáři neskončili ve městě
s poloplným barelem a se všemi cestami vedoucími do města už vyasfaltovanými?
Důsledky zalití náměstí a několika přilehlých čtvrtí do asfaltu by byly
pro cestáře jistě nemilé...
Napište program, který pro zadané propojení měst cestami rozhodne, zda je možno
cesty podle popsaných pravidel vyasfaltovat, a pokud ano, vypíše jednu
z možností, jak rozvrhnout, která dvojice cest bude asfaltována ze kterého
barelu.
Na prvním řádku vstupního souboru asfalt.in se nacházejí dvě celá čísla N a
M oddělená mezerou (1 ≤ N ≤ 10 000 a 1 ≤ M ≤ 40 000), kde N
určuje počet měst a M počet cest v Hipopotámii. Dále ve vstupním souboru
následuje M řádků popisujících jednotlivé cesty. Každý řádek obsahuje dvě celá
čísla A a B oddělená mezerou – čísla měst (města číslujeme od jedné
do N), mezi kterými cesta vede. Předpokládejte, že mezi každými dvěma městy se
lze po cestách dostat (pokud ne přímo, tak přes jiná města).
Výstupní soubor asfalt.out bude buď obsahovat jediný řádek s textem no,
pokud neexistuje způsob, jak vyasfaltovat všechny cesty a neskončit s poloplným
barelem v nějakém městě, nebo bude obsahovat M/2 řádků s popisem postupu
asfaltování. Každý řádek postupu bude popisovat využití jednoho barelu
s asfaltem, tj. bude obsahovat tři celá čísla oddělená mezerou, která
představují po řadě: číslo města, ve kterém má asfaltování začít, číslo města,
do kterého se má pokračovat a číslo města, ve kterém má asfaltování skončit.
Nezapomeňte, že každá cesta má být vyasfaltována právě jednou!
Příklad 1:
asfalt.in
3 3
1 2
2 3
3 1
asfalt.out
no
Příklad 2:
asfalt.in
5 8
1 5
1 4
1 3
1 2
3 2
3 4
4 5
4 2
asfalt.out
5 1 4
5 4 3
4 2 3
3 1 2
Řešení
20-3-6 Hrady, hrádky, hradla (12 bodů)
Milí řešitelé, nyní už víme, jak vlastně obvody fungují, jak jsou rychlé
a energeticky náročné. V dnešním pokračování našeho seriálu si povíme něco
o reprezentaci dat v binární podobě, tj. pomocí jedniček a nul.
Reprezentací dat zde myslíme nějaký způsob, jakým převést čísla nebo i jiné
údaje do nul a jedniček, se kterými už umíme pracovat. Nejednodušší způsob, jak
to udělat je dvojková neboli binární číselná soustava. Čísla se pak mezi
desítkovou a dvojkovou soustavou převádějí následovně:
Dvojková → Desítková
Vezmeme číslo zapsané ve dvojkové soustavě a budeme postupně brát cifry po
jedné zprava doleva. Každou z nich vynásobíme dvojkou umocněnou na počet
cifer, které jsou od aktuální cifry vpravo. Pro číslo 101010 to bude vypadat
následovně: 0·20 + 1·21 + 0·22 + 1·23 + 0·24 + 1·25 = 2 + 8 + 32 = 42.
Jelikož a0·20 + a1·21 + a2·22 + … + an·2n lze
přepsat jako a0 + 2(a1 + 2(a2 + 2(… + 2an )… ))), funguje i
následující jednodušší převodní algoritmus: začneme nejlevější číslicí, znásobíme
ji dvěma, přičteme další číslici, výsledek znásobíme dvěma, a tak dále.
Desítková → Dvojková
Pokud je zadané číslo sudé, zapíšeme si nulu, v případě, že číslo je liché, zapíšeme jedničku
a od čísla jedničku odečteme. Pak číslo vydělíme dvěma a postup zopakujeme.
Jedničky a nuly budeme zapisovat zprava doleva
tak dlouho, až se naše číslo stane nulou. Číslo 13 bychom převáděli takto:
| číslo desítkové | číslo dvojkové | výpočet |
| 13 | 1 | (13-1)/2 |
| 6 | 01 | 6/2 |
| 3 | 101 | (3-1)/2 |
| 1 | 1101 | (1-1)/2 |
Všimněte si, že tento postup je vlastně předchozí postup pro převod
z dvojkové soustavy spuštěný pozpátku.
Jiný používaný způsob, jak kódovat čísla do jedniček a nul, je kód BCD
(Binary Coded Decimal). Myšlenka je následující: Když se rozhodneme trochu
plýtvat, klidně můžeme kódovat desítková čísla po číslicích. Přitom na každou číslici
použijeme 4 bity, a to tak, že využijeme 10 kombinací z 16 možných. Číslo 1394
bychom zapsali jako 0001 0011 1001 0100. Díky mírnému plýtvání jsme
si značně zjednodušili práci, tedy aspoň v případech, kdy čísla daleko častěji
rozebíráme na číslice, než s nimi počítáme. (Pěkný příklad jsou třeba digitální
hodinky – ty musí umět číslo zobrazovat na displeji, ale jinak stačí umět
přičítat jedničku.)
Někdy se také potřebujeme vypořádat s tím, že pokud přenášíme nějaký údaj
do jiného obvodu (třeba po počítačové síti, a nebo ho ukládáme na disk),
může se cestou trochu poškodit – některé bity se mohou změnit z nul
na jedničky nebo naopak. Tehdy se samozřejmě hodí umět chybu odhalit, nebo
dokonce automaticky opravit. Zkusme si třeba na konec binárního čísla přidat
nulu nebo jedničku tak, aby celkový počet jedniček v čísle byl sudý (tomu
se říká paritní bit). Pokud v takovém čísle nastane jedna chyba, ihned ji
odhalíme, jelikož vždy vznikne číslo s lichým počtem jedniček. Existuje
spousta sofistikovanějších kódů, které dokáží detekovat nebo opravovat větší
počty chyb, ale my si už místo dalšího povídání raději naservírujeme nové
úložky.
Úložky
Vaším úkolem nyní bude vymyslet obvod na detekci chyb, který bude testovat
dělitelnost třemi (taková kontrola chyb je o něco silnější než parita).
1) Navrhněte a nakreslete obvod, který pro číslo zadané v binární reprezentaci zjistí,
zda je dělitelné třemi. [6 bodů]
2) Úkol je stejný, ovšem čísla jsou na vstupu v BCD reprezentaci. [6 bodů]
Řešení