Pátá série dvacátého prvního ročníku KSP
Celý leták v PDF.
- Termín série: 31. 5. 2009
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 21-5-1: Polomáčené mrakodrapy
- 21-5-2: Banky
- 21-5-3: Krávy
- 21-5-4: Zákony
- 21-5-5: Cestovní šavle
- 21-5-6: Kržnc
Přinášíme vám již poslední sérii tohoto ročníku. Nastává finále, které všechno rozhodne. Přejeme příjemnou zábavu a hodně štěstí!
Pátá série dvacátého prvního ročníku KSP
Píše se rok 2050. Konečně se podařilo rozpustit poslední zbytky ledovců a hladiny světových oceánů se netriviálně zvedly. Hlavní město hlavního telenovelového státu se začalo potýkat s problémy. A právě v těchto časech začíná příběh našeho hlavního hrdiny Chulia.
21-5-1 Polomáčené mrakodrapy (10 bodů)
 Na hlavní město našeho státu – Chuenos Aires – se valí pohroma. Chulianovo
rodné město, dříve tak prosperující metropole nudlovitého tvaru, bude
brzy zatopeno stoupající vodou z oceánů. Úředníci vlády
teď nutně potřebují vědět, kolik úseků města si bude i během záplav
moci naladit pravidelnou večerní telenovelu.
Na hlavní město našeho státu – Chuenos Aires – se valí pohroma. Chulianovo
rodné město, dříve tak prosperující metropole nudlovitého tvaru, bude
brzy zatopeno stoupající vodou z oceánů. Úředníci vlády
teď nutně potřebují vědět, kolik úseků města si bude i během záplav
moci naladit pravidelnou večerní telenovelu.
Město Chuenos Aires si můžeme představit jako jednu dlouhou ulici, na které je namačkán mrakodrap vedle mrakodrapu. Mrakodrapy jsou tak natěsno, že nemají mezi sebou žádné mezery. Každý mrakodrap (s plochou střechou) má kladnou celočíselnou výšku měřenou v telemetrech nad mořem. Chodník má výšku právě 0 telemetrů nad mořem.
Předpověď počasí hlasí, že zatím jsou všechny mrakodrapy v pořádku, ale počínaje dnem 1 se výška moře zdvihne o jeden telemetr denně. Postupem času se některé věžáky zatopí až po špičku a z hlavní ulice v Chuenos Aires zbudou pouze souvislé úseky mrakodrapů, které ční nad hladinu. Každému takovému úseku stačí jedna anténa na přijímání televize. Vaším úkolem je spočítat, kolik antén bude v jednotlivých dnech potřeba (tedy kolik zbude souvislých bloků mrakodrapů v onen den).
Tato úloha je praktická, takže bližší informace o formátu vstupu programu i ukázkový příklad najdete v CodExu. Povídání o tom, jak se praktická úloha odevzdává, najdete například v zadání úlohy 21-1-2 „Optimalizace kotlů“.
Když i nejvyšší mrakodrap v Chuenos Aires, ve kterém Chulio bydlel, začal být těžko obyvatelný, protože jeho obyvatelé museli každé ráno vyhánět z postele žraloky, rozhodl se Chulio odjet na venkov, kde by začal žít nový život.
A jak se rozhodl, tak udělal. Odešel z města a začal pracovat na kávové plantáži. Tam se brzy seznámil s krásnou Ochechulínou. Začali snít o tom, že se jednou vezmou a sami budou vlastnit podobnou plantáž, každé ráno budou vstávat se šálkem kávy a úsměvem nad dalším dnem. Bohužel zloduch Choachým jim každé snění zkazil, neboť je stále budil před ránem a nutil pracovat.
Z Choachýma se stal úhlavní nepřítel a Chulio s Ochechulínou začali snovat plán pomsty.
Jejich plán byl geniální. Propracovaný do nejmenšího detailu. Skoro. Neměli na něj peníze. A protože prací ještě nikdo nezbohatl, začali vymýšlet, jak na to. Naštěstí bankovní servery v té době ne zcela plánovaně chlazené mořskou vodou vykazovaly o něco vyšší chybovost, a tak stačilo jen trocha šikovnosti a investice ve výši 10 pesos k odlehčení kont nenasytných bankéřů.
21-5-2 Banky (10 bodů)
Aby se podobné odlehčování nekonalo příliš často, nebo pokud možno už nikdy, požádali vás nenasytní bankéři, abyste jim pomohli. Jak vlastně Chulio zbohatnul? Banka obchoduje valutami a má vypsané kurzy pro některé dvojice měn. Banka je hodná a za směnu si neúčtuje žádný poplatek. Pokud ale není dostatečně opatrná, může se stát, že vhodnou posloupností směn získáte více, než jste měli na začátku. Váš program tedy dostane na vstupu směnný kurz banky a měl by rozhodnout, zda je na jeho základě možné zbohatnout výše popsaným způsobem.
Například pro 4 měny a kurzy (zápis X→Y Z znamená, že za 1 jednotku měny X získáte Z jednotek měny Y):
1->2 0.8 2->3 24
2->1 0.8 2->4 129
1->4 0.08 3->1 0.5
lze např. posloupností výměn 1->2, 2->3 a 3->1 (za jednu jednotku
měny 1 získáte po této sérii výměn 9,6 jednotek) na úkor banky vydělat.
Takže v tuto chvíli by měl program odpovědět, že směnný kurz je prodělečný. Pokud
žádná taková posloupnost neexistuje, váš program by měl odpovědět, že banka bude opět
o něco bohatší.
Chulio s Ochechulínou skoupili celou plantáž a mohli dokonat svůj dokonale zosnovaný plán – Choachýma přeřadili na tu nejhorší práci: ochutnávač kávy. Je jasné, že Choachýmovi tato práce nedovolila pořádně se vyspat, takže nedostatkem spánku psychicky narušený Choachým začal vymýšlet svůj plán pomsty.
Chulio a Ochechulína vedli šťastný život. Zcela se jim splnil sen. To ale netrvalo dlouho. Bratr Chulia Chosé se dozvěděl o Chuliově úspěchu a přicestoval za ním. Hodný Chulio zaměstnal Chosého a pověřil ho úkolem vybudovat vedle plantáží farmu pro dobytek.
21-5-3 Krávy (9 bodů)
Navrhovat stáje pro krávy není vůbec jednoduchý úkol. Navíc máte-li omezené množství prostředků. Chuliův kravín se skládá z řady boxů stejných rozměrů těsně vedle sebe. V každém boxu může bydlet nejvýše jedna kráva. Tyto boxy jsou z jedné (stejné) strany vždy otevřené. Vaším úkolem je rozmístit před tyto boxy závory boxy tak, aby každý, ve kterém bydlí kráva, byl přehrazený.
Závor ale máte k dispozici pouze určitý počet. Naštěstí každá závora může být libovolně dlouhá a není zakázáno přehradit i boxy, ve kterých žádná kráva nebydlí.
Navrhněte algoritmus, který pro zadaný kravín (počet boxů a rozmístění krav v jednotlivých boxech) nalezne takové rozmístění závor, aby součet jejich délek (jeden box má šířku jeden telemetr) byl minimální a všechny boxy s kravami byly přehrazeny. Pokud má úloha více řešení, stačí nalézt libovolné z nich.
Příklad: Mějme kravín s 8 boxy, číslovanými od 1 do 8. Krávy bydlí v boxech 1, 3, 5, 6 a 8 a k dispozici máme 3 závory. Pak je jedno z optimálních řešení přehradit jednou závorou boxy 1 až 3, druhou závorou 5 až 6 a třetí závorou box 8. Celková délka závor tak bude 6 telemetrů, neboť první závora přehrazuje 3 boxy, druhá 2 a třetí pouze jeden.
Takto například vypadají boxy 1, 2 a 3:
==============================================
! (__) ! ! !
! (oo) ! ! !
! /------\/ ! ! /------\ !
! / ! !! ! ! / ! (__) !
! * /\---/\ ! ! * /\---(oo) !
! ~~ ~~ ! ! ~~ \/ !
----------------------------------------------
Chosé byl ze začátku spokojený, a tak navrhoval stáje, obdělával pastviny, kupoval dobytek a farma vzkvétala. Jenže brzy začal pociťovat závist, protože dřel na svého bratra, který jenom popíjel kávu a trávil čas s krásnou Ochechulínou, po které Chosé stále více toužil.
Ochechulínu to uvádělo do rozpaků, ale příliš se návrhům Chosého nebránila, neboť narozdíl od Chulia neměl hrb, měl obě ruce stejně dlouhé a také měl delší …vlasy.
Ani Choachým během probdělých dní a nocí nemarnil čas a stále promýšlel svůj plán pomsty. Protože zbohatnout stejně jako Chulio již nebylo možné, chtěl k pomstě využít to, čeho měl nejvíc. Šarm. Rozhodl se svést Chulia, následně jej obžalovat z obtěžování a potom převzít vládu nad farmou i Ochechulínou.
Plán se mu podařil a Chulio skončil se zlomeným srdcem u soudu. Zatímco se Chulio pokoušel prokličkovat ve spleti zákonů, Choachým seč mohl pospíchal na farmu.
21-5-4 Zákony (12 bodů)
Obhájit se u soudu bývá podobné jako vymotat se z hustého a temného lesa. Všude kolem jsou stromy, totiž jednotlivé zákony, a čím těžší přestupek jste spáchali, tím obtížnější je se mezi nimi prosmyknout a proniknout z právního lesa zpět na svobodu.
Napište program, který na vstupu dostane popis spleti zákonů a velikost vašeho přestupku. Program pak odpoví, zda je možné se u soudu obhájit nebo ne.
Program dostane dvě čísla: přirozené N a kladné reálné R. Číslo N udává počet zákonů a R velikost vašeho hříchu. Dále dostane vaše výchozí souřadnice v lese X a Y a popis jednotlivých stromů (zákonů). Každý strom je zadán svými souřadnicemi. Všechny souřadnice jsou reálná čísla.
Hodnota R určuje, jak nejvíc se na cestě ven z lesa můžete přiblížit k libovolnému stromu. Předpokládejte, že stromy mají nulový průměr a jsou nekonečně vysoké a že výchozí pozice je vždy korektní, tzn. že na začátku nejste v kolizi s žádným stromem.
Úlohu lze formulovat i tak, že zjišťujete zda se koule o poloměru R může vykulálet ven ze zadaného lesa.
A co znamená dostat se ven z lesa? Třeba mít možnost dostat se do bodu se souřadnicemi (∞,∞).
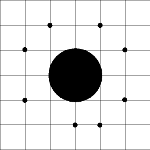
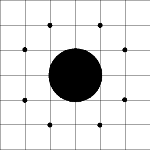
Například pro N=8, R=1,1, X=0, Y=0 a stromy (-2,1), (-1,2), (1,2), (2,1), (2,-1), (1,-2), (0,-2), (-2,-1) se z lesa dostat lze.
Pro N=8, R=1.1, X=0, Y=0 a stromy (-2,1), (-1,2), (1,2), (2,1), (2,-1), (1,-2), (-1,-2), (-2,-1) se z lesa dostat nejde.
 Choachým dorazil, právě když vládu nad Ochechulínou přebíral Chosé, využívaje k tomu svých dlouhých vlasů. Takové setkání prostě muselo skončit soubojem.
Choachým dorazil, právě když vládu nad Ochechulínou přebíral Chosé, využívaje k tomu svých dlouhých vlasů. Takové setkání prostě muselo skončit soubojem.
Chosé proklál Choachýma svojí cestovní šavlí.
21-5-5 Cestovní šavle (10 bodů)
Určitě znáte klasický zednický metr. Ten se skládá z několika segmentů. Vždy dva sousední segmenty jsou spojeny pantem, takže je metr možné rozložit, pokud měříme nějakou vzdálenost, nebo složit, pokud ho přenášíme. Přesně tímto způsobem funguje Chosého cestovní šavle. Jenom s tím rozdílem, že délky segmentů nejsou stejné.
Napište program, který pro zadané délky jednotlivých segmentů šavle zjistí, zda je možné šavli poskládat do pouzdra zadané délky. Program dostane dvě přirozená čísla N a L. Číslo N je rovno počtu segmentů šavle a L je délka pouzdra. Následuje N přirozených čísel, které postupně udávají délky segmentů šavle zleva doprava. Můžete předpokládat, že N i L ≤ 10000. Program by měl odpověď „Ano“ nebo „Ne“ podle toho, zda je možné šavli složit do pouzdra.
Například pro N = 3, L = 6 a délky 6,3,3 je možné šavli poskládat. Pro stejné N i L, ale pro délky 6,3,4 šavli poskládat nelze.
Mezitím se od soudu vrátil Chulio. Když se dozvěděl, co se tu stalo, využil toho, že se Chosému stále nedařilo složit šavli zpět do pouzdra a proklál s ní i svého proradného bratra. Od té doby již žil Chulio s Ochechulínou šťastně až do konce …až do konce 14223. dílu, kdy se ukázalo, že předchozích 14221 dílů bylo jenom snem a Chulio s Ochechulínou se probouzí do dalšího pracovního dne na farmě.
21-5-6 Kržnc (12 bodů)
Ke konci spěje nejen tento ročník KSP, ale i náš seriál o programování na počítači Rapl (připomínáme, že seriálovou úlohu je nutné řešit ve speciálním programovacím jazyku, jehož popis najdete v zadání úlohy 21-1-6). Už jsme si vyzkoušeli psát co nejkratší programy, ba i programy, které za běhu použijí co nejméně instrukcí. Na závěr zkusíme, jak šetřit paměť, kterou program potřebuje k výpočtu.
Mějme nějaký neorientovaný graf (viz kuchařka u 3. série), jehož každý
vrchol sousedí s právě čtyřmi hranami. Takový graf můžeme RAPLu
popsat následovně: očíslujeme si vrcholy od 0 do n-1 a do pole S naskládáme
čísla sousedů jednotlivých vrcholů tak, že sousedé vrcholu i budou
uloženi v S[4*i], S[4*i+1], S[4*i+2] a S[4*i+3].
Bude nás zajímat, zda v tomto grafu existuje kružnice, která obsahuje
každý vrchol právě jednou. Napište program v RAPLu, který pro libovolný
zadaný graf odpoví v registru k jedničkou, pokud taková kružnice existuje,
a jinak nulou.
Váš program by měl použít co nejméně paměti. Množství použité paměti přitom definujeme jako počet paměťových buněk (registrů či prvků polí), do kterých program během výpočtu zapsal. Pokud tedy vstup pouze čtete a nepřepisujete, jeho velikost se nepočítá. Záleží nám i na multiplikativních konstantách – mezi 2n a 10n buněk je podstatný rozdíl. Naproti tomu nemusíte vůbec brát ohled na časovou složitost, může být klidně megasuperexponenciální :-)
Při programování si tentokrát můžete odpustit nezajímavé detaily, stačí nám, když dostatečně výstižně popíšete, co přesně do paměti jak uložíte a jak s tím budete zacházet.
[+2 body] Ukažte, jak úlohu vyřešit s méně než n/19 paměťovými buňkami, pokud víte, že každý vrchol sousedí jen s třemi hranami.