U přesné kopie prvního elektronkového počítače ENIAC z roku 1946, jak hlásal holografický panel, jej přivítal jeden z techniků. „Problém je s tímhle panelem,“ řekl a ukázal na desku se žárovičkami. Ta, jak si John pamatoval, neměla u původního ENIACu žádný klíčový význam, ale měla sloužit pro vizualizaci výpočtu. Běžní lidé chtěli vidět, že ta ohromná konstrukce něco dělá a blikající světla byla nejlepší. Od té doby také několik desítek let přežívala představa počítače, jako stroje s chaoticky blikajícími kontrolkami.
Čtvrtá série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
- Termín série: 9. dubna 2012 8:00
- Termín CodExové úlohy: 10. dubna 2012 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 24-4-1: Iniciály předků
- 24-4-2: Sledování exponátů
- 24-4-3: Cinkání skleničkami
- 24-4-4: Vozíky ve skladu
- 24-4-5: Holografické projektory
- 24-4-6: Starý kód
- 24-4-7: Čtvercové bombardování
- 24-4-8: O hrách a číslech
24-4-1 Iniciály předků (10 bodů)

 Tým techniků chce nechat na panelu se žárovičkami postupně zobrazovat nějaký
řetězec znaků, aby panel pěkně blikal a upoutalo to procházející lidi. Panel je
tvořený spoustou sloupců žárovek a každý sloupec umí zobrazit jeden znak.
Tým techniků chce nechat na panelu se žárovičkami postupně zobrazovat nějaký
řetězec znaků, aby panel pěkně blikal a upoutalo to procházející lidi. Panel je
tvořený spoustou sloupců žárovek a každý sloupec umí zobrazit jeden znak.
Technici si jako správní hračičkové sepsali iniciály všech svých předků až do 20. století a ty chtějí nechat zobrazovat na panelu.
Nicméně, čím je řetězec delší, tím déle se musí vkládat do paměti počítače. Technici si chtějí ušetřit práci, a tak by chtěli znát takovou jeho nejkratší část, jejímž opakováním se dá vypsat celý řetězec.
Vaším úkolem je tedy napsat program, který si na vstupu přečte řetězec znaků (složený z velkých písmen anglické abecedy), nalezne v něm nejkratší úsek, jehož opakováním vznikne celý řetězec, a vypíše jeho délku.
vstup odpověď
ABABAB 2
ABABA 5
AAA 1
Tato úloha je praktická a řeší se ve vyhodnocovacím systému CodEx. Přesný formát vstupu a výstupu, povolené jazyky a další technické informace jsou uvedeny v CodExu přímo u úlohy.
„Než přišly na scénu různé obrazovky, velmi oblíbenou metodou výstupu byl tisk na různý tiskárnách či elektronických psacích strojích,“ začal průvodce. „Neuměly samozřejmě tisknout nějakou grafiku, natožpak trojrozměrně, jako ty dnešní. Ale zvládaly celkem rychle tisknout znaky. Tiskárny zvládající tisk nějakých jiných obrazců než znaků přišly až v 60. letech 20. století.“
Přešel k prvnímu exponátu „Nejdříve se používaly jehličkové tiskárny, které se stylem fungování podobaly psacím strojům. Pomocí jehliček přitiskávaly barevnou pásku na papír… pozor, pane, ta páska pořád barví. Až teprve počátkem 70. let se začal prosazovat laserový tisk. Ten funguje v základě tak, že se pomocí laseru na správných místech vybije elektrostaticky nabitý rotující selenový válec. Toner se přichytí pouze na vybitá místa, pohybem válce následně přilne na papír. A nakonec se toner do papíru zapeče.“
„A co inkoustové tiskárny, myslel jsem, že přišly dříve než laserové?“
„To je častý omyl. Inkoustové tiskárny se začaly prosazovat až počátkem 80. let, ale protože byly levnější na výrobu, prosadily se hlavně v domácím prostředí. Fungují tak, že se inkoust v tryskách tiskové hlavy zahřeje pomocí maličkého elektrického tělíska asi na 300°C a pak vlivem tlaku ve velké rychlosti vystříkne z trysky na papír.“
Výklad o tiskárnách byl ale přerušen jedním ze strážných muzea. „Problém šéfe, spadnul nám systém zjišťování polohy exponátů. Víme, kde exponát je, ale systém už nevyhodnotí, jestli je pořád uvnitř budovy, nebo ne.“ To tu ještě scházelo, pomyslí si John, ale nedávaje na sobě znát únavu posledních dní se vydává za strážným do velínu bezpečnosti, kde si nechává vysvětlit fungování celého systému, tedy spíše jeho nefungování. Bude nutné ho celý přepsat.
24-4-2 Sledování exponátů (8 bodů)
 Hranice muzea počítačů má tvar nekonvexního mnohoúhelníku. Na
sledovaném exponátu je připevněno čidlo, které vysílá jeho aktuální polohu
(určenou například pomocí GPS).
Hranice muzea počítačů má tvar nekonvexního mnohoúhelníku. Na
sledovaném exponátu je připevněno čidlo, které vysílá jeho aktuální polohu
(určenou například pomocí GPS).
Měli byste strážným v muzeu pomoci tím, že vymyslíte postup, jak zjistit, jestli je exponát ještě na území muzea, nebo ne. Jediné, co máte k dispozici, je poloha exponátu a posloupnost vrcholů hranice muzea.
Byla už skoro půlnoc, když John konečně vítězoslavně klepl do potvrzovací klávesy a zvedl se od počítače. Tak, další problém vyřešený, poklepal se v duchu po rameni. Teď ale musím stihnout ten banket v aule muzea.
Rychle proběhl skrz kancelář, vzal na sebe společenský oblek a pospíchal, ať stihne alespoň půlnoční přípitek.
24-4-3 Cinkání skleničkami (8 bodů)
Přípitky ve 22. století mají několik základních pravidel. Stojí se v kruhu, všichni si musí cinknout se všemi a dále se nesmí cinkat „křížem“ (když si dva páry lidí cinkají, nesmí se jim zkřížit ruce).
A aby to nebylo tak jednoduché, cinká se v taktech. Vždy na úder gongu si člověk buď cinkne s někým, nebo zůstane stát. Pak na další úder gongu s dalším člověkem a tak dále, dokud si necinkne se všemi.
Vás zajímá, kolik nejméně takovýchto taktů bude potřeba, aby si navzájem cinklo N lidí a také správný postup, jakým si budou cinkat. Nezapomeňte dokázat, že to na méně taktů nejde.
Druhý den ráno přišel John do práce s hrozným bolením hlavy – neměl to včera s těmi přípitky přehánět. V kanceláři si jenom vzal něco na bolest, počkal, až prášek zabere, a pak šel zkontrolovat konečné přípravy otevření expozice. Jen co vešel do hlavní haly, všiml si podivného ruchu u dveří skladu.
„Jako by nám někdo nepřál otevření,“ uvítal ho vrchní skladník. „Máme výpadek proudu ve skladu. A to zrovna potřebujeme navézt několik beden s těmi, jak se jim říkalo… monitory, myslím. Jsme schopni nabít každému vozíku baterie trochou energie, ale chtělo by to nějak optimalizovat jejich trasy, jinak to prostě z toho skladu nestihneme vyvézt.“
24-4-4 Vozíky ve skladu (10 bodů)
Moderní sklad 22. století je obsluhován pouze automatickými elektrickými vozíky. Ty normálně čerpají energii z rozvodné sítě vozíků, ale při výpadku této sítě jsou schopné fungovat i na baterie. Samotný sklad je spleť křižovatek a uliček. Uličky jsou obousměrné, mohou se křížit i víceúrovňově a setkávají se pouze na křižovatkách.
Navíc pod podlahou některých uliček jsou silnoproudé vodiče, které svým magnetickým polem ztěžují vozíkům průjezd. Silnoproudé vodiče jsou napojeny na oddělený okruh, výpadek je tedy neovlivní. Samozřejmě v nich „teče“ střídavý proud, který indukuje (střídavé) magnetické pole – to v jedné půlce svojí periody vozík zpomaluje, ve druhé zrychluje.
Skladníci zjistili, že by toto pole mohli využít – nastavili vozíky tak, aby jim průjezd libovolnou uličkou trval vždy stejně dlouho, a to právě půlku periody střídavého proudu. Délka cesty a magnetické pole ovlivňují jen spotřebu energie.
Vzhledem k výpadku napájení se hlavní skladník pokouší optimalizovat trasy jednotlivých vozíků a potřebuje od vás najít energeticky nejúspornější trasu (tj. trasu, při níž vozík spotřebuje nejméně energie z baterií) mezi dvěma křižovatkami, které si určí.
Na vstupu dostanete mapu skladu popsanou jednotlivými křižovatkami spolu s uličkami, které mezi nimi vedou. Každá ulička má danou spotřebu energie při průjezdu. Dále dostenete seznam uliček, pod kterými vedou silnoproudé vodiče – můžete si je představit tak, že každý lichý průjezd libovolnou křižovatkou zdvojnásobí jejich energetickou náročnost, každý sudý průjezd ji vrátí do počátečního stavu.
Samozřejmě víte i odkud kam má vozík jet – tedy startovní a cílovou křižovatku. Nejúspornější trasu vypište jako pořadí křižovatek. Nezapomeňte, že skladníci spěchají, vozík tedy nesmí nikdy stát.
Příklad: máme 5 křižovatek očíslovaných 0 až 4 a chceme vozík přepravit z 0 do 1. Všechny uličky obsahují silnoproudé vodiče a vedou mezi křižovatkami (v závorce je energie spotřebovaná při průjezdu): 0 a 1 (21), 0 a 2 (10), 2 a 3 (5), 3 a 4 (2), 2 a 4 (5), 4 a 1 (10).
Nejvýhodnější je použít cestu 0→2→3→4 →1, při níž se spotřebuje 39 jednotek energie. Kdyby se jelo uličkou z 0 rovnou do 1, stálo by to 42 jednotek; cesta 0→2→4 →1 by stála 45 jednotek.
Když se ze skladu konečně dostaly i poslední palety s monitory, John si oddechl. Mezitím, co se hlavní skladník zabýval vozíky, si John dokonce něco stihl nastudovat i o prastarých monitorech.
Jak psali ve starém propagačním letáku, první monitory byly jednobarevné, napevno vestavěné do počítačů a nebylo možné k jakémukoliv počítači připojit jakýkoliv monitor. Za první univerzální grafickou kartu se standardizovaným adaptérem se dá považovat až Monochrome Display Adapter (MDA) z roku 1981 od Intelu, k němuž se dal přes konektor podobný pozdějšímu VGA (ale s méně piny) připojit jakýkoliv monitor s tímto konektorem. MDA umožňoval výstup 80 sloupců na 25 řádků znaků.
Později se objevily i karty podporující nejen znakový, ale i grafický režim a v roce 1987 přišel standard Video Graphics Array (VGA) se svým konektorem, který přežil přes 25 let. Stále se ale jednalo o analogový výstup. První digitální výstup do připojeného monitoru přišel až v roce 1999 společně se standardem a konektorem Digital Visual Interface (DVI).
John přestal pročítat brožuru, rychle nalistoval poslední kapitolu se základním rozebráním principu dvou nejrozšířenějších zobrazovačů přelomu tisíciletí a četl. Starším byla technologie katodové trubice, tedy CRT monitory. Fungovaly na stejném principu jako tehdejší televize. Elektronové dělo vysílalo proud nabitých částic, které byly usměrňovány velkými elektromagnety, na dopadovou plochu zvanou stínítko. Tam se pomocí látky zvané luminofor proud elektronů měnil na viditelné světlo.
Druhou technologií, která se začala kvůli ceně prosazovat až počátkem 90. let a k jejímuž masovému rozšíření došlo až po přelomu tisíciletí, byla technologie tekutých krystalů LCD. Pracovala na principu zastiňování světla. Za deskou z tekutých krystalů bylo osvětlovací těleso, produkující bílé viditelné světlo. Samotná deska z tekutých krystalů pak v závislosti na natočení krystalků buď světlo v daném bodě propouštěla, nebo ne. Natočení krystalků v jednotlivých bodech bylo řízeno pomocí slabého elektrického proudu.
„Teda, ti si s tím vyhráli,“ hvízdl obdivně John a odložil brožuru. Pak se podíval směrem ke vstupu do expozice, kde měla skupinka pracovníků problém s naprosto současnou zobrazovací technikou, s holografickými projektory.
24-4-5 Holografické projektory (12 bodů)
Do expozice muzea se vstupuje dlouhou chodbou, v níž jsou na jedné stěně instalovány holografické projektory. Každý projektor promítá na přesně určené místo na druhé stěně chodby.
Žádné dva promítané obrazy na stěně se sice nepřekrývají a žádné dva projektory nejsou na jednom místě, ale může se stát (a vzhledem k návrhům uměleckého designéra na uspořádání se stává dost často), že se paprsky nějakých dvou projektorů cestou kříží. A aby u holografických projektorů nedošlo k nechtěné interferenci a rozmazání obrazu, musí v takovém případě pracovat oba projektory na jiné frekvenci.
Technik, který už tak má bolení hlavy z návrhů designéra, zároveň chce, aby bylo použito co nejméně frekvencí, protože je to jednodušší na údržbu. Když se projektory nekříží, mohou mít klidně stejnou frekvenci. Ale žádné dva křížící se projektory nemůžou pracovat na stejné frekvenci.
Navrhněte tedy postup, jak co nejrychleji určit, na jakých frekvencích mají pracovat které projektory, tak, aby počet použitých frekvencí byl co nejmenší. Od designéra dostanete pouze rozmístění promítaných obrazů na stěně (například očíslované podle pořadí odpovídajících projektorů na druhé stěně).
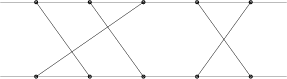
Příklad: pro vstup 3 1 2 5 4 se paprsky na stejné frekvenci nekříží
například při rozdělení: frekvence 1 – projektory 1, 2, 4, frekvence 2 –
projektory 3, 5. Viz obrázek:
„Tak vidíte, že to šlo. A vypadá to pěkně.“ usmál se John na designéra, když mu konečně vymluvil některé jeho šílenější nápady s umístěním holografických projektorů. Rozloučili se a John se vydal dál, až úplně dozadu celého prostoru připravované expozice. Tam sídlila výstava netradičních výstupních zařízení.
Na podstavci u vstupu stál Braillský řádek. Jak říkal popisek, tato pomůcka pro nevidomé mohla zobrazovat až 80 znaků v Braillově písmu. Zobrazení jednotlivých znaků měly na starost většinou malé elektromagnety, které nadzvedly odpovídající výstupky. Nevidomý tedy mohl procházet jakýkoliv textový obsah na obrazovce a na Braillském řádku si ho přečíst.
Další zajímavostí byla ukázka technologie, která se začala rozvíjet na přelomu prvního a druhého desetiletí 21. století, takzvaných generátorů vůně. Vstupní data pro tyto věci mohla pocházet buď ze speciálního programu, nebo z chemického čidla na druhé straně komunikační linky. Generátor pachu pak z několika základních chemických vůní (podobně jako monitor z několika základních barev) poskládal pach nebo vůni, která se tomu co nejvíce blížila.
„Něco takového bych si domů asi nepořídil,“ řekl John a pak leknutím uskočil, neboť se hned vedle něj náhle rozsvítila velká obrazovka plná spousty znaků. „Promiňte pane, jenom tady procházíme stará záznamová média a koukáme, co by šlo zobrazit na těchto obrazovkách, hned to dám pryč.“
„Počkejte!“ vyhkrl John, v němž se probudila zvídavost. „Vždyť to je kus nějakého starého programového kódu, k čemu asi… hmm… počkejte, už je mi to asi jasné. Ale proč je to napsané takhle neefektivně?“
24-4-6 Starý kód (9 bodů)
Pracovníci muzea počítačů nalezli na jednom starém disku následující kód. Zkuste zjistit, co vlastně kód dělá, a zamyslete se nad tím, jestli by nešel přepsat nějak efektivněji.
#include <stdio.h>
#include <stdlib.h>
#define MAX_H 1000000
#define MAX_V 1001
typedef struct {
int x, y;
}H;
int N, M;
H h[MAX_H];
int v[MAX_V][MAX_V];
int p[MAX_V];
int f[2*MAX_V];
short b[MAX_V];
int main() {
scanf("%d%d", &N, &M);
if (N>MAX_V || M>MAX_H) {
printf("Chybny vstup.\n");
return 1;
}
for (int i=0; i<M; i++) {
int x, y;
scanf("%d%d", &x, &y);
if (x>N || x<1 || y>N || y<1) {
printf("Chybny vstup.\n");
return 1;
}
h[i] = (H){x, y};
v[x][p[x]++] = y;
v[y][p[y]++] = x;
}
printf("Vysledny seznam:\n");
for (int k=0; k<M; k++) {
int a = 0;
int z = 0;
for (int i=1; i<=N; i++)
b[i] = 0;
b[h[k].x] = 1;
f[z++] = h[k].x;
while (a<z && b[h[k].y]==0) {
int q = f[a++];
for (int i=0; i<p[q]; i++) {
if (b[v[q][i]]==0 && !(q==h[k].x
&& v[q][i]==h[k].y)) {
f[z++] = v[q][i];
b[v[q][i]] = 1;
}
}
}
if (b[h[k].y]==0)
printf("%d %d\n", h[k].x, h[k].y);
}
return 0;
}
Vedle něj byl objeven druhý, podobný kód, u kterého byla poznámka, že až na nepodstatný rozdíl ve čtení vstupu dělá to samé:
import sys
MAX_H = 1000000
MAX_V = 1001
v = []; p = []; f = []; b = []; h = []
for j in range(MAX_V+1):
v.append([]); b.append(0); p.append(0)
for j in range(2*MAX_V):
f.append(0)
N, M = raw_input().split(' ')
N = int(N); M = int(M)
if N > MAX_V or M > MAX_H:
sys.exit("Chybny vstup.")
for i in range(M):
x, y = raw_input().split(' ')
x = int(x); y = int(y)
if(x>N or x<1 or y>N or y<1):
sys.exit("Chybny vstup.")
h.append((x, y))
v[x].append(y); p[x] += 1
v[y].append(x); p[y] += 1
print "Vysledny seznam:"
for k in range(M):
a = 0; z = 0
for i in range(1,N+1):
b[i] = 0
b[h[k][0]] = 1
f[z] = h[k][0]; z += 1
while(a<z and b[h[k][1]] == 0):
q = f[a]; a += 1
for i in range(p[q]):
if b[v[q][i]] == 0 and not (
q == h[k][0] and v[q][i] == h[k][1]
):
f[z] = v[q][i]; z += 1
b[v[q][i]] = 1
if b[h[k][1]] == 0:
print h[k][0], h[k][1]
První helmy virtuální reality se začaly objevovat koncem 80. a počátkem 90. let. V podstatě šlo o helmu se dvěma malými obrazovkami, pro každé oko jedna. Ve spojení ještě například s rukavicemi poskytujícími hmatovou odezvu se tak člověk mohl ponořit do světa virtuální reality.
Helmy se ale díky své ceně a váze nikdy příliš neuplatnily. Na přelomu prvního a druhého desetiletí nového tisíciletí jejich funkci částečně převzaly technologie trojrozměrných brýlí a odpovídajících obrazovek, které byly mnohem dostupnější než drahé helmy.
„Nechcete si třeba vyzkoušet nějakou starou hru?“ zeptal se technik a aniž by čekal na odpověď, spustil hru s nejnápadnějším názvem.
24-4-7 Čtvercové bombardování (13 bodů)
 Představte si, že máte velké město a chcete ho srovnat se zemí. Třeba
protože se vám už nelíbí a chcete místo starých domů postavit nové, moderní.
Představte si, že máte velké město a chcete ho srovnat se zemí. Třeba
protože se vám už nelíbí a chcete místo starých domů postavit nové, moderní.
Máte k dispozici bombardér se speciální demoliční bombou. Na demoličních bombách je zajímavé to, že jsou pečlivě sestrojené tak, aby srovnaly se zemí pouze přesně danou čtvercovou oblast. A protože jste nakoupili kvalitní demoliční bomby, bouchají navíc pouze směrem na východ a jih.
Tedy pokud shodíte demoliční bombu s rázem D do místa [x,y], budou zdemolovány všechny budovy ve čtverci vymezeném body [x,y] a [x+D,y+D], ale nic jiného. Protože ale chcete demolovat efektivně, bude lepší si vše předem propočítat.
Pro zjednodušení budeme budovy považovat za body – na vstupu dostanete jejich počet B < 250 000 a jejich souřadnice [xi; yi]; -109 < xi, yi < 109. Zkuste vymyslet program, kterého se budete moci ptát, kolik budov bude zbouráno, když do místa [x,y] hodíte bombu s rázem 0 < D < 2 · 109. Všechny souřadnice jsou celočíselné.
Počítejte s tím, že těchto dotazů bude program dostávat řádově statisíce, takže se pokuste, aby odpovědi na dotazy byly rychlé i za cenu delšího úvodního předpočítání.
„To teda byla hra!“ smál se John, když sundaval helmu. „Děkuju.“
Technik s úsměvem převzal helmu a podíval se na obrazovku, kde svítilo „Úroveň New York dokončena, přejete si pokračovat?“
I nadešel poslední den před otevřením, do slavnostního přestřižení pásky zbývalo již jen několik hodin a vše konečně vypadalo připravené. Projektory svítily, panel se žárovičkami blikal, vozíky ve skladu opět jezdily a sledovací systém exponátů spokojeně předl.
Nestrhne se na poslední chvíli ještě nějaká pohroma? Bude konečně dopřáno Johnovi přestřihnout v klidu slavnostní pásku? Prozradím vám, že ano. Co se ale stane několik sekund po přestřižení pásky, to je už jiný příběh. Možná někdy příště…
Od klávesnice se s Vámi loučí váš dnešní průvodce muzeem počítačů
24-4-8 O hrách a číslech (15 bodů)
 Vítejte u dalšího dílu herního seriálu. Podrobněji rozvineme Conwayovu teorii
her, konkrétně se naučíme hry porovnávat a některým přiřazovat čísla.
Vítejte u dalšího dílu herního seriálu. Podrobněji rozvineme Conwayovu teorii
her, konkrétně se naučíme hry porovnávat a některým přiřazovat čísla.
Zopakujme si nejdůležitější pojmy z minula. Zajímají nás hry dvou hráčů označovaných jako Levý a pRavý. Vše jsme si dosud ukazovali na dominování, které spočívá v pokládání dominových kostek do čtvercové mřížky. Levý pokládá svisLe, pravý vodoRovně.
Dále jsme rozdělili hry (přesněji řečeno pozice) do čtyř tříd dle vítěze:
- vyhrané pozice: vyhraje hráč, který bude táhnout jako první; třída V
- prohrané hry: začínající hráč prohraje; třída P
- pozice levého: levý vždy vyhraje, ať začne kdokoliv; třída L
- pozice pravého: analogicky k levému; třída R
Důležité bylo sčítání pozic, které jsou nezávislé (nelze zahrát do obou najednou), přičemž začínající hráč si vždy může vybrat, kam potáhne.
V tomto díle se nám bude hodit rovnost her: hry G a H se rovnají, tedy G = H, pokud dopadnou stejně, když k oběma přičteme libovolnou jinou hru. Rovněž budeme využívat i obrácené hry značené -G, v níž si hráči vymění možné tahy, které od teď povedou do podobně obrácených pozic. V dominování odpovídá -G otočení herního plánu o 90°.
Posledním úkolem v minulém díle bylo ukázat, že z G = H vyplývá, že G - H je prohraná hra. Tvrzení však platí i opačně: pokud G - H je prohraná hra, pak G = H.
Když víme, které hry se rovnají, jak poznat, že nějaká hra je lepší pro levého než jiná? Opět budeme zkoumat hru G - H. Je-li to pozice levého (levý vyhraje, ať začíná kdokoliv), pak G je pro levého lepší než H, což se zapisuje jako G > H.
Pokud je pozice G - H v třídě R, tak G < H. Dvojicím her, pro něž G - H je pozice vyhraná pro začínajícího hráče, budeme říkat neporovnatelné, což se značí G ∥ H.
Tímto jsme si definovali částečné uspořádání na hrách. Stejně jako pro jiná uspořádání z G < H a H < I vyplývá G < I (analogicky pro pravého).
Číslování her
Než začneme číslovat hry, doplníme ještě abstraktní zápis her, v němž bude pozice G vypadat takto: G= {GL | GP}. GL je množina pozic, kam může táhnout levý hráč, obdobně GP jsou hry po tazích pravého hráče. Jelikož takto suchá definice může snadno zmást, podívejte se na obrázek: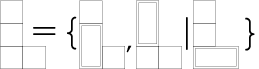
Nyní se můžeme pustit do přiřazování čísel hrám. Ty budou vyjadřovat, jak moc velkou má levý nebo pravý výhodu v pozici oproti soupeři. Velikost čísla bude udávat, kolik tahů má jeden z hráčů navíc (kupodivu to vyjde někdy neceločíselně).
Kladná čísla budou znamenat výhodu levého a záporná výhodu pravého. Všimněte si, že pozici levého hráče nemůžeme přiřadit záporné číslo, jelikož v ní má alespoň malou výhodu levý. Obdobně pozice z třídy R nemohou dostat kladné číslo.

V pozici vlevo má levý hráč jeden tah navíc, hra dostane tedy číslo 1. V pozici vpravo má pravý dva tahy a levý nic, proto -2. V abstraktním zápise se hra s kladným číslem n dá zapsat jako {n-1 | } (levý hráč může táhnout do hry s číslem n-1), hra n < 0 analogicky jako { | n+1}.
Když máme kladná i záporná čísla, je logické se ptát, co bude 0. V souladu s definicí kladných i záporných her znamená 0, že žádný z hráčů nemá výhodu, ani ten, co je na tahu, čili je to prohraná pozice.
Nejjednodušší taková hra je { | } (žádný hráč nemá tah) a každá prohraná hra se rovná 0. (Pro prohranou hru G není těžké ověřit, že G = 0. Nejsnadněji asi důkazem, že G - 0 je prohraná hra.)
Na začátku jsme tvrdili, že čísla her mohou být neceločíselná. Konkrétně mohou být jen tzv. diadická racionální, tedy zlomky n/2m v základním tvaru, kde n je celé číslo a m přirozené (včetně 0).
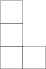
Na následujícím obrázku je hra s hodnotou 1/2, v níž levý získá tah navíc, jen když začíná pravý:
Jak zjistit hodnotu dané pozice, když máme rozebrány hry, do nichž hráči mohou táhnout, nám řekne pravidlo jednoduchosti.
Mějme hru G = {GL | GR}, přičemž všechny tahy obou hráčů vedou do pozic, jež jsou čísla, a každý tah levého vede do pozice s číslem menším, než mají všechny pozice po tazích pravého hráče (formálně ∀GL ∈ GL, ∀GR ∈ GR: GL < GR). Potom G je nejjednodušší číslo x, nacházející se mezi hodnotami pozic levého a pravého (GL < x < GR).
Nejjednodušší v minulém odstavci znamená, že x je diadické, čili n/2m v základním tvaru, m je co nejmenší (preferují se celá čísla) a mezi čísly se stejným m se vybere to s menší absolutní hodnotou n.
Příklady:
- {-1 | 1} = 0
- {-100 | 10} = 0
- {-42 | -4} = -5
- {0 | 1} = 1/2
- {{1 | -1} | {1 | -1}} = 0 (je to prohraná hra)
- {1 | -1} není číslo
- {-5 | -10} není číslo (hra je však vyhraná pro pravého)
- {0 | 0} není číslo
Poslední hra v seznamu, {0 | 0}, je nejjednodušší vyhranou hrou a značí se *.
Všimněte si, že některé hry levého či pravého jsou čísla a jiné ne. Žádná vyhraná hra však není číslo (výhodu má ten, kdo začne, ne vždy levý nebo pravý) a naopak každá prohraná hra se rovná 0, i když se to nemusí nahlédnout přes pravidlo jednoduchosti.
Her, které nejsou čísla, je hodně. Například ↑= {0 | *}, analogicky ↓= {* | 0} = -↑. Hrám {a | b}, kde a > b, se říká přepínač, speciálně ±a = {a | -a} pro a > 0.
Co se týče uspořádání dle výhodnosti pro levého (či pravého), tak platí například (ověření necháme jako cvičení):
- {-10 | 10} = {-1 | 1} = 0,
- {1 | 2} < {1 | 6},
- ↑> 0 a symetricky ↓< 0,
- * ∥ 0,
- ±1 ∥ 0,
- ±10 ∥ ±5.
Bylo by nyní potřeba ukázat, že hry, jež se rovnají, mají stejná čísla (mají-li vůbec nějaká). Nebo že součet her G a H má číslo rovné součtu čísel G a H.
Celkově by však důkazy zabraly možná celou sérii, takže případné zájemce odkáži na literaturu a internet (viz níže). Jejich hlavním důsledkem je, že lze libovolně zaměňovat hru a k ní příslušející číslo.
Místo důkazů zkusíme hry zjednodušovat. Podívejme se třeba na hru G = {3,2,*,0 | 4,6,8,10}. Levý nemá žádný důvod táhnout do 2, * nebo 0, podobně pravý potáhne určitě do 4, tedy G = {3 | 4} = 3,5.
Obecně lze v možnostech levého vyškrtat pozice horší pro levého než nějaká jiná pozice a analogicky mezi tahy pravého škrtáme pozice větší než nějaká jiná. Formálně zapsáno (pro možnosti levého): je-li G = {A, B, … | C, D …}, přičemž A > B nebo A = B, pak G = {A, … | C, D …} (nerovnosti mezi hrami jsou ty samé, co byly definovány na začátku tohoto dílu).
Úkol 1 [4b]
Mějme hromádku n sirek. Je-li n sudé, levý na tahu odebírá dvě sirky a pravý jednu. Je-li n liché, vezme levý jednu sirku a pravý dvě. Určete číslo hry pro každé n ≥ 0.
Úkol 2 [5b]
Výše jsme si ukazovali pozici v dominování s hodnotou 1/2 (označme ji G). Ověřte, že G + G = 1. Dále nalezněte v dominování pozici H, jež není číslo, ale H + H = 1.
Úkol 3 [6b]
Hra Padající domino se hraje s bílými a černými dominovými kostkami postavenými v řadě za sebou. Tah hráče spočívá ve výběru jedné své kostky a jejím shození doleva nebo doprava, přičemž díky tomu spadnou všechny kostky ve směru, kam padala.
Levý hraje s bíLými kostkami, pravý s čeRnými a opět platí, že prohrál ten, kdo nemůže táhnout. Pro jednoduchost budeme posloupnost kostek zapisovat jako řetězec s písmeny B a C zastupujícími bílé a černé kostky. Například z pozice CBC má levý dva tahy, oba vedoucí do pozice C.
Pro hry BCBBBBC a BBCCBC najděte co nejjednodušší abstraktní zápis, jež neobsahuje konkrétní pozice, ale jen čísla, *, ↑ apod. (tedy třeba {{4 | 2} | -6}). Vyškrtáváte-li nějakou možnost, je třeba zdůvodnit, proč.
Tím jsme zakončili spíše neformální úvod do Conwayovy teorie her. Toto odvětví matematiky je však podstatně košatější, vynechali jsme dost důkazů (i zajímavých!), teploty a teploměry her (určování, jak moc výhodné je do hry zahrát) a mnoho dalších zajímavých věcí.
Co se týče praktické využitelnosti teorie, je na ní založený algoritmus pro řešení koncovek v Go nazvaný Decomposition search.
Prohloubit své znalosti teorie si můžete mimo jiné přečtením Winning Ways for your Mathematical Plays od Berlekampa, Conwaye a Guye a On Numbers and Games od Conwaye (ani jedna z nich bohužel nemá český překlad).
Mimochodem, hry v zápise {A, B, C, … | P, Q, R, …} jsou tzv. nadreálná čísla (jejich speciálním případem jsou i reálná čísla), o nichž se dočtete více na Wikipedii.
Hračičkům doporučujeme program CG Suite, v němž lze zadávat pozice z různých her (nebo zapsané nadreálným číslem) a nechat určit jejich hodnotu, teplotu a další vlastnosti. (To může sloužit i pro kontrolu řešení úkolů, bude však třeba vše zdůvodnit.)
Příště se můžete těšit na návrat výpočetní části seriálu započaté v první a druhé sérii (algoritmy Minimax a Alfa-beta ořezávání). Nově nabyté znalosti si budete moct vyzkoušet na analýze jedné deskovky, kterou bude možné hrát online.