První série dvacátého devátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 29-1-1: Připálené placky
- 29-1-2: Kupecké počty
- 29-1-3: Střídání zbraní
- 29-1-4: Zběsilý útěk
- 29-1-5: Lučištníci
- 29-1-6: Štítové kouzlo
- 29-1-7: Stromy kolem nás
 29-1-1 Připálené placky (Zadání)
29-1-1 Připálené placky (Zadání)
Než se pustíme do samotného řešení, tak si úlohu trochu upravíme. Namísto hromady placiček otočených tím či oním způsobem budeme otáčet pole jedniček a nul.
Jednička bude representovat placičku otočenou správně (tedy spálením dolů), nula otočenou špatně. Jedinou dovolenou operací je překlopení (jedničky na nulu a nuly na jedničku) všech hodnot od první až do nějaké i-té (včetně). Tedy vlastně negace prefixu (souvislé podčásti začínající na levém okraji) pole.
Hned na začátku si je třeba uvědomit jednu velmi důležitou věc ze zadání. Nechceme otáčení hodnot, tedy překlápění placiček, opravdu provést. Stačí nám říct, kde všude by to bylo třeba.
Toto pozorování způsobí, že naše řešení bude nakonec lineární a ne kvadratické, jak by se na první pohled mohlo zdát.
Pro začátek se pokusme na pole hodnot podívat jako na soustavu stejnorodých úseků jedniček a nul. Snadno si za chvilku dokážeme, že překlápět hodnotu má smysl jen u prefixů, které končí právě v přechodech mezi souvislými úseky jedniček a nul (či obráceně).
Určitě platí, že v konečném stavu, tedy když jsou všechny hodnoty jedničky, nejsou v poli žádné přechody. Celá věž je totiž jeden stejnorodý úsek.
Otočením hodnot úseku končícím na rozhraní určitě zrušíme jeden přechod. Změníme totiž hodnotu těsně před rozhraním a beze změny ponecháme tu těsně za ním. Což, pokud máme jen dvě možné hodnoty, které se před tím lišily (a vytvářely tak přechod), znamená, že nyní musí být stejné.
Operací také nikterak neovlivníme jiné úseky před nebo za původním rozhraním. Těch za rozhraním se totiž ani nedotkneme a těm před pouze otočíme hodnoty.
Pokud by úsek, v našem případě prefix, který operací změníme, končil mimo přechod, tak nejenže se žádného rozhraní nezbavíme, ale dokonce vytvoříme nové. Znegujeme totiž hodnoty první poloviny nějakého předtím stejnorodého úseku, čímž ho nutně rozdělíme na dvě nové části s různými hodnotami.
Všem ostatním úsekům před koncem prefixu pak pouze přehodíme hodnoty, tedy žádný neodstraníme, a na ty dále za nikterak nezměníme. Skončíme tedy jen s přidáním jednoho přechodu. Je vidět, že má smysl uvažovat jen o úsecích končících v místech již existujících přechodů.
Algoritmus je již nyní snadný. Vytvoříme si pomocnou proměnnou, která si bude pamatovat typ posledního úseku. Na začátku ji nastavíme na hodnotu prvního prvku v poli. Následně pro každý další prvek pole uděláme jednu ze dvou věcí.
Pokud je jeho hodnota stejná jako v pomocné proměnné, tak pokračujeme normálně dál. Pokud je jiná, tj. nastal zlom, tak zahlásíme otočení až do posledního indexu (včetně) a pomocnou proměnnou aktualizujeme hodnotou prvku, který právě zpracováváme; tedy hodnotou která je těsně za zlomem.
Takhle dojdeme až na konec, kde ještě zkontrolujeme, zda je poslední hodnota 1. Když není, tak zahlásíme operaci nad celým polem, tj. otočení všech placek.
Algoritmus zjevně potřebuje pouze jeden lineární průchod plackami. Časová složitost je tedy O(N), kde N je počet placek.
U paměové složitosti záleží na tom, jak si ji zavedeme. Pokud si povolíme číst vstup postupně a stejně tak i vypisovat výstup, tak nám stačí konstantní množství paměti. V průběhu si totiž stačí pamatovat onu pomocnou proměnnou. Pokud však použijeme staromdní definici, tak si musíme pamatovat celý vstup najednou, což automaticky znamená i prostorovou složitost O(N).
 29-1-2 Kupecké počty (Zadání)
29-1-2 Kupecké počty (Zadání)
Každý kupec ví, kolik zaplatil, tedy se domluví, napíšou všechny částky na papír a spočítají z nich průměr. To je částka, kterou každý z nich chce nakonec zaplatit. Někteří zaplatili víc, jiní méně. V seznamu kupců tedy od výše každé investice odečteme průměr.
Tím dostaneme pro každého kupce buďto kladné číslo – o tolik zaplatil do projektu víc, a tedy tolik má od ostatních dohromady dostat – nebo záporné číslo – o tolik zaplatil méně, a tedy tyto peníze nějak rozdělí svým kolegům.
Můžou nám vyjít i nuly. Nulový kupec zaplatil právě tolik, kolik zaplatit měl, a nemusí se tedy s nikým vyrovnávat. Vyřadíme jej ze seznamu, neboť takových kupců by klidně mohlo být docela dost a zbytečně by kazili časovou i paměťovou složitost zbytku algoritmu.
Kupci se mezi sebou budou vyrovnávat tak, že se vždy potká nějaký dlužník (to je ten, co má platit) s nějakým věřitelem (to je ten, co má peníze dostat) a zaplatí si nějakou částku.
Kolik si můžou zaplatit? Označíme-li celkovou výši dluhu jako D a celkovou výši pohledávky jako P, můžou se vyrovnat nejvýše o min(D, P). Kdyby si chtěli snad předat víc peněz, buď dojde k předlužení, nebo k přeplacení, což zadání zakazuje.
| N |
| 2 |
Zadání nám tedy dovoluje provést N transakcí. To je ale velmi milé, protože každou transakcí dokážeme alespoň jednoho kupce vynulovat. Stačí když převedeme nejvyšší možnou částku: pokud min(D,P) = D, právě jsme vynulovali dlužníka; pokud min(D,P) = P, vynulovali jsme věřitele.
Rýsuje se nám tedy jednoduchý algoritmus:
Nejprve si spočítáme, kolik měl každý zaplatit, a rozdělíme vstup na dluhy a pohledávky, to vše v čase (O(N)). Poté, dokud budou nějaké pohledávky a dluhy zbývat, vybereme libovolný dluh a libovolnou pohledávku (třeba první ze seznamu) a převedeme maximální možnou částku. Když už žádné pohledávky a dluhy nejsou, máme hotovo a můžeme se jít klouzat.
Proč to funguje? Každým převodem vynulujeme alespoň jednoho kupce, tedy s konečným množstvím převodů budou vynulováni všichni. Též z toho plyne, že převodů provedeme nejvýše N-1, takže jsme splnili zadání.
Jak je to rychlé? Předzpracování trvá O(N). Každý krok pak trvá konstatní čas: výběr dluhu, výběr pohledávky i samotné vyrovnání.
Paměťová složitost zahrnuje uložení několika proměnných, vstupu velikosti N a dvou seznamů o celkové délce taktéž N, celkem tedy O(N).
Někteří řešitelé tvrdili, že je potřeba vstup setřídit, nedokázali ale přijít s žádným rozumným argumentem, proč by to mělo být potřeba. Je to lákavé, ale můžeme netřídit a díky tomu si nezavléct do složitosti logaritmus (O(N log N) místo O(N), a to za to stojí, ne?
Jiní se mě zase snažili přesvědčit, že po každé transakci musíme proběhnout celé pole a vyházet z něj ty, kdo už platili. To však není vůbec potřeba. Vždyť jediné dva, kterých se to týká, jsme právě měli v ruce. Takovým postupem se dalo dosáhnout až (pro tuto úlohu jistě impozantní) složitosti O(N2).
Též se objevilo několik řešení, kde řešitelé porušovali podmínky dané v zadání, například vesele přepláceli, případně si dokonce pořídili banku, která všechno zprostředkovala. Někteří se tohoto prohřešku dopustili skrytě, jiní to dokonce drze deklarovali. Pro odvahu postavit se organizátorům a hrdě řešit jinou úlohu jsem však neměl valného pochopení a uděloval pouze body útěchy.
 Úlohu jsme zadali úmyslně s požadavkem na maximálně dvojnásobný počet
převodů. Důvod je prostý. Optimální řešení totiž získáme tak, že bychom našli
rozdělení množiny kupců do co nejvíce podmnožin tak, aby součet v každé
z podmnožin byl nulový. Nicméně už jenom otázka, jestli vůbec existuje
podmnožina, jejíž součet je nulový, je NP-úplný problém
(anglicky Subset Sum Problem).
Jistě pochopíte, že po vás nemůžeme chtít vymyslet řešení takové úlohy v polynomiálním čase.
Úlohu jsme zadali úmyslně s požadavkem na maximálně dvojnásobný počet
převodů. Důvod je prostý. Optimální řešení totiž získáme tak, že bychom našli
rozdělení množiny kupců do co nejvíce podmnožin tak, aby součet v každé
z podmnožin byl nulový. Nicméně už jenom otázka, jestli vůbec existuje
podmnožina, jejíž součet je nulový, je NP-úplný problém
(anglicky Subset Sum Problem).
Jistě pochopíte, že po vás nemůžeme chtít vymyslet řešení takové úlohy v polynomiálním čase.
 29-1-3 Střídání zbraní (Zadání)
29-1-3 Střídání zbraní (Zadání)
Na začátku si seřadíme gardisty podle výšky od nejnižšího po nejvyššího. Představme si, že si v tomto pořadí chodí vybrat kopí. Označme si mi počet kopí kratších než i-tý gardista (počítáme od nuly). První gardista si může vybrat ze všech kopí, které je schopen používat, má tedy m0 možností.
Druhý gardista je schopen používat m1 různých kopí. Ale vybrat si může pouze z m1 - 1, protože jedno z nich už si vzal první gardista (první gardista je menší než druhý, tedy kopí, které si vzal, by mohl používat i druhý, ten tak o jednu možnost přišel).
Analogicky třetí gardista dokáže používat m2 kopí, ale dvě z nich už si zabrali první dva gardisté, má tedy na výběr z m2 - 2 možností. Obecně i-tý gardista si může vybrat z mi - i kopí.
Počet možností, které má i-tý gradista, nezávisí na tom, jaká kopí si vybrali předchozí. Tady je vidět, proč je důležité gardisty brát v pořadí od nejmenšího. Kdyby byl první gardista vyšší než druhý, počet kopí, které zbudou na druhého gardistu, by závisel na tom, jak vysoké kopí si vzal první.
Takhle víme, že pro každou z m0 možností výběru prvního gardisty existuje právě m1-1 možností volby druhého. Celkem tedy je m0 ·(m1-1) možností, jak si může vybrat první dvojice.
Obecně když provádíme několik výběrů po sobě a počet možností, ze kterých v každém kroku vybíráme, nezávisí na volbách v předchozích krocích, je celkový počet možností prostě součinem počtů možností v jednotlivých krocích. Tomuto principu se říká pravidlo kombinatorického součinu.
Dostáme tedy celkem
(kde N je počet gardistů) možností, jak si gardisté mohou rozdělit kopí.
Dlužno podotknout, že celkový počet možností samozřejmě nezávisí na tom, v jakém pořadí si gardisté vybírají kopí. Jen když si představujeme, že si vybírají v pořadí od nejmenšího, je o dost snažší možnosti spočítat.
Teď v podstatě stačí dosadit do vzorečku. K tomu bychom ale nejdřív potřebovali spočítat jednotlivá mi. To je celkem jednoduché. Na začátku si kromě gardistů i kopí seřadíme vzestupně podle délky. Teď budeme postupně procházet jednotlivé gardisty a průběžně si udržovat index největšího kopí menšího než aktuální gardista (tento index odpovídá právě mi).
Když přejdeme na následujícího gradistu, tento index zvyšujeme, dokud nenarazíme na kopí vyšší než on. Takto spočítáme všechna mi jedním průchodem přes obě pole v lineárním čase. Podrobněji ve vzorovém programu. Jde o podobný princip jako při slévání setříděných posloupností.
Celková časová složitost je O(N log(N)), protože tolik času strávíme tříděním a zbytek stihneme v lineárním čase. Paměťová složitost bude lineární.
Většina z vás na základní myšlenku přisla. Co jste často opomíjeli, je zdůvodnit, proč řešení funguje. Z výše uvedeného vzorečku není bez komentáře vůbec vidět, že by měl platit. Po přečtení spousty řešení nebylo ani jasné, proč vlastně vstup třídí, když se poté nikdy nezmínily, k čemu to využijí, či dokonce že bez třídění by vzoreček neplatil. Zdůvodnění jsme tentokrát považovali za poměrně důležitou součást úlohy (už proto, že algoritmus samotný je poměrně jednoduchý) a patřičně strhávali body.
Také jste se málokdy zamysleli, co se stane, když neexistuje žádná možnost, jak gardistům kopí rozdat (například některá kopí jsou vyšší než všichni gardisté). V takovém případě se může stát, že některé ze závorek mi - i vyjdou nulové či dokonce záporné.
V tomhle případě platí, že pokud některá z nich vyjde záporná, bude mezi nimi i nějaká nulová (rozmyslete si), tedy dosazením do vzorečku dostanete správný výsledek: nulu. Ale není to vůbec zřejmé a slušelo by se nad tím v řešení zamyslet.
 Ještě se zmíníme o jednom detailu, který je asi přijatelné na úrovni
KSP příliš neřešit: výsledný počet možností
může být velmi velké číslo. Počítáme součin N čísel velkých až N
(v nejhorším případě jsou všechna kopí kratší než všichni gardisté), tedy výsledek
může být velký řádově až NN, což se kromě nejmenších vstupů do běžných
celočíselných typů nevejde.
Ještě se zmíníme o jednom detailu, který je asi přijatelné na úrovni
KSP příliš neřešit: výsledný počet možností
může být velmi velké číslo. Počítáme součin N čísel velkých až N
(v nejhorším případě jsou všechna kopí kratší než všichni gardisté), tedy výsledek
může být velký řádově až NN, což se kromě nejmenších vstupů do běžných
celočíselných typů nevejde.
S tím se musíme nějak vypořádat v závislosti na tom, čeho přesně chceme dosáhnout. Pokud by nám výsledek například stačil přibližně či řádově, nejjednodušším řešením je použít nějaký typ s plovoucí čárkou (float, double), který umí uchovávat velmi velká čísla, byť s omezenou přesností, a zacházet s nimi v konstantním čase a prostoru.
Druhou možností je počítat s velkými čísly poctivě přesně. Ale to už obecně nezvládneme v konstantním čase: číslo velké řádově K zabere v paměti místo L=O(log K) a vynásobení dvou takovýchto čísel zvládneme poměrně jednoduchým algoritmem v čase zhruba O(L1.5) (jde to i rychleji).
V našem případě L = O(log NN) = O(N log N), tedy jedno násobení stihneme v čase O(N1.5 log 1.5 N), počítáme N součinů, takže celková časová složitost vzroste na O(N2.5 log 1.5 N), paměťová na O(N log N).
 29-1-4 Zběsilý útěk (Zadání)
29-1-4 Zběsilý útěk (Zadání)
Úloha byla velmi jednoduchá, až triviální. Prostě pro každou úsečku projdu všechny hustolesy, zjistím, se kterým se protíná, spočítám dráhu, kterou urazím hustolesem a kterou řídkolesem, obojí vydělím příslušnou rychlostí a výsledné časy sečtu.
Takové řešení má časovou složitost O(U·H), kde U je počet úseček a H je počet hustolesů. Tyto hodnoty mají být řádově stejné, aneb U=O(N), H=O(N), celková složitost je tedy O(N2). Není to moc? Je to moc. Áha. Úloha nebyla tak jednoduchá a triviální, jak by se na první pohled mohla zdát. Přesto i na triviálním řešení šlo nasbírat nemálo bodů.
Připomeňme si techniku zametání roviny přímkou. Projdeme celou oblast například zdola nahoru a poznamenáme si, kde začíná a kde končí který hustoles. Na to si musíme seznam hustolesů setřídit, což zabere O(H log H). Seznam začátků a konců hustolesů si označíme jako SZKH.
Tahle metoda se nám hodí při procházení lesem. Na začátku stojím v bodě y0, spočítám si, které hustolesy procházejí přímkou o souřadnici y=y0, a budu tedy znát jejich seznam. Bude se hodit, aby byl setříděný, zabere nám to jen O(H log H).
Pak posunu přímku do y1. Abych ji nemusel počítat celou odznova, podívám se do SZKH a zpracuju všechny události, které jsou mezi y0 a y1. A celou dobu se přitom dívám, jestli se na přímce náhodou neobjevil nějaký hustoles se souřadnicí mezi x0 a x1, a pokud ano, tak jej hned podrobím zkoumání, jestli náhodou nebyl proťat právě zpracovávanou úsečkou.
Pak posunu stejným způsobem přímku do y2 (a zpracovávám druhou úsečku), pak do y3 … Postupně tak zpracuju všechny úsečky na vstupu.
Implementačně se pro účely ukládání stavu na přímce bude patrně hodit použít nějaký vyvažovaný vyhledávací strom, třeba červenočerný. Složitost zpracování každé úsečky pak bude O(K log H), kde K je počet kroků, které je potřeba udělat.
Tím jsme si ale vůbec nepomohli, protože úsečka zrovna mohla vést z levého okraje území na pravý, takže stejně musíme vyzkoušet všechny hustolesy, i když víme, že protnout má nejvýše jeden.
| (x1 - x0)(yα- y0) |
| y1 - y0 |
| (x1 - x0)(yβ- y0) |
| y1 - y0 |
Co se stane v obdélníku, který jsme si vytyčili souřadnicemi (xα, yα, xβ, yβ)? Především uvnitř něj nemůže ležet žádná vodorovná hrana žádného hustolesa. Kdyby v našem obdélníku snad chtěla ležet horní nebo dolní hrana nějakého hustolesa, musela by být vložena též v SZKH, ale pak bychom se naším obdélníkem vůbec nemohli zabývat, protože mezi yα a yβ by ještě existovalo nějaké yυ, takže by yα a yβ nebyly hned po sobě jdoucí polohy zametací přímky, tedy máme spor, kterým jsme dokázali, že tento obdélník je horních a dolních hran hustolesů zcela prost.
Pokud tedy nějaký hustoles v obdélníku leží, vždy obsáhne celou jeho výšku, a tedy se vždy musí protnout s úsečkou jdoucí po jeho úhlopříčce. Stejně tak obráceně, pokud nějaký hustoles v obdélníku neleží, tak se rozhodně mezi souřadnicemi yα a yβ nemůže protnout se zkoumanou úsečkou.
Kromě hustolesů tedy budeme mít na naší zametací přímce ještě bod, který bude označovat průsečík zkoumané úsečky s aktuální přímkou, a při každém posunutí přímky s ním pohneme na správné místo a zkontrolujeme, jestli jsme tím náhodou netrefili hustoles.
Co když ale úsečka vede shora dolů, takže musíme projít všechny polohy zametací přímky? Jednou by to nevadilo, ale mohly by takto vést třeba všechny úsečky a pak bychom si se složitostí vůbec nepomohli. Stále totiž každý posun zametací přímky zabere O(log H) času, takže bychom si zhoršili složitost na O(U·H log H). To nám je platné jak mrtvému zimník.
Všimneme si tedy, že při posouvání zametací přímky sem-tam počítáme pořád dokola totéž – její stav.
Pořídíme si tedy datovou strukturu, která dokáže nějak rozumně uložit všechny možné polohy zametací přímky, a zároveň nebude přehnaně velká. Pokud jsme ochotni obětovat až O(H2) paměti, stačí si postupně uložit všechny stavy zametací přímky. Jenomže na vygenerování O(H2) dat potřebujeme také O(H2) času, takže jsme zase nahraní.
Ne tak docela. Ukládáním všech stavů zametací přímky bychom zase ledacos ukládali redundantně, takže si pořídíme nějaký vhodný druh komprese. Každý hustoles budeme reprezentovat dvěma seznamy ukazatelů: seznamem levých sousedů a pravých sousedů. Seznam levých sousedů říká pro každý interval souřadnice y nejbližší sousední hustoles směrem vlevo. Analogicky vypadá seznam pravých sousedů.
Seznamy postavíme tak, že projdeme zametací přímkou přes všechny události v SZKH. Na začátku není v oblasti žádný hustoles, ale vyrobíme si dva virtuální se souřadnicemi xλ= -∞, xπ= ∞.
Když potkáme událost „začátek hustolesa“, podíváme se, mezi které dva jiné hustolesy jej máme přidat. (Vždycky tam budou alespoň ty dva virtuální.) Do seznamu levých sousedů pravého hustolesa a do seznamu pravých sousedů levého hustolesa tedy přidáme odkaz na právě přidávaný hustoles, do seznamu levých sousedů právě přidávaného hustolesa vložíme odkaz na levý hustoles a do seznamu pravých sousedů právě přidávaného hustolesa vložíme odkaz na pravý hustoles.
Když potkáme událost „konec hustolesa“, podíváme se taktéž, mezi kterými dvěma jinými hustolesy byl. Seznamy levých a pravých sousedů odebíraného hustolesa uzavřeme, do seznamu levých sousedů pravého hustolesa přidáme levý hustoles a do seznamu pravých sousedů levého hustolesa přidáme pravý hustoles.
Jak dlouho to trvá? Každý posun zametací přímkou potřebuje O(log H) času kvůli aktualizaci jejího stavu. K tomu vyrobíme 4 nebo 2 nové odkazy, což je konstanta, která logaritmem nehne. Celkem nás bude vytvoření datové struktury stát O(H log H) času, což je stále stejně jako počáteční potřeba setřídění.
Jak velká bude zkonstruovaná datová struktura? To se dá spočítat z algoritmu, kterým ji vyrábíme. Každý hustoles vygeneruje v SZKH jednu událost začátku a jednu událost konce hustolesa. Zpracováním těchto dvou událostí vznikne v datové struktuře právě 6 nových odkazů. Datová struktura tedy spotřebuje celkem O(H) paměti. To vypadá nadějně.
Na vstupech, které generovalo naše odevzdávátko, už tato úprava běžela dostatečně rychle na získání plného počtu bodů, protože drtivá většina zadaných úseček byla v porovnání s velikostí oblasti velmi krátká. Při zpracování každé úsečky totiž stačilo projít několik málo odkazů – prázdných oblastí, přes které zrovna procházela, i když byla třeba poměrně dlouhá.
Stále se nám sice může stát, že budeme při zpracování každé úsečky projít přes O(H) odkazů, takže jsme si pomohli zpátky na O(U·H) v nejhorším případě.
Bylo by fér spočítat, že v průměrném případě na tom budeme líp, nicméně počítat statistiku nad úsečkami a obdélníky v rovině je poněkud ošemetné, jak naznačuje kupř. Bertrandův paradox, tak si to raději odpustíme.
Program s řešením v čase O(N2) (C)
Program s rychlejším řešením v čase až O(N2 log N) (C)
 29-1-5 Lučištníci (Zadání)
29-1-5 Lučištníci (Zadání)
Na vstupu mějme N lučištníků. Zleva doprava si je očíslujme od 1 do N, stejně jako cíle, na které se míří. Platí, že cíl s číslem k se nachází naproti střelci k. Jako ck si označme číslo cíle lučištníka k.
Mnoho z vás se snažilo najít nejlepší řešení tímto způsobem: pro každého lučištníka našlo počet drah, s nimiž se ta jeho kříží, a následně postupně odstraňovalo lučištníky s největším možným počtem křížení. Takový postup ale obecně nefungoval. Například v zadání na obrázku byste mohli odstranit i druhého lučištníka, který do správného řešení očividně patří, ačkoliv se jeho dráha kříží se dvěma dalšími drahami.
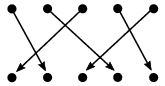
Uvedeme si řešení běžící v čase O(N2) a to následně zlepšíme. Zaveďme pojem nekřížící se skupina pro takovou podmnožinu střelců, že jejich dráhy se navzájem nekříží.
Pro každého lučištníka k teď chceme najít co největší nekřížící se skupinu Ak, pro níž platí, že k do ní náleží (tj. bude střílet) a jinak se skládá jen ze střelců nalevo od k. Všimněte si, že v této skupině míří na nejpravější cíl právě lučištník k.
Projdeme teď lučištníky zleva a pro každého budeme chtít spočítat číslo dk, což je velikost skupiny Ak.
Jistě A1 = {1} a tedy d1 = 1. Pro k > 1 vytvoříme skupinu Ak tak, že prodloužíme nějakou předešlou skupinu (každá větší skupina je nutně rozšířením nějaké předešlé skupiny: stačí si uvědomit, že odebráním střelce nejvíce napravo dostaneme kratší skupinu). Jistě chceme vzít takovou s co největším počtem střelců; stále ale musí platit, že se dráhy nekříží. Pokud dáme dohromady všechna pravidla, vyjde nám, že dk = maxdi + 1, kde i < c a ci < ck. Právě druhé pravidlo zajistí, že dráha k-tého střelce není v konfliktu s ostatními drahami.
Po doběhnutí cyklu pak nejvyšší dk označuje maximální počet lučištníků, kteří mohou střílet najednou. Pokud chceme znát konkrétní čísla střelců, stačí algoritmus jednoduše rozšířit: vždy po vypočtení nového dk si zapamatujeme číslo střelce, rozšířením jehož skupiny vznikla Ak. Na konci cyklu pak najdeme nejvyšší dk a od něj tyto zpětné odkazy projdeme a vypíšeme.
| N(N+1) |
| 2 |
Existuje však lepší řešení. Nejprve si pro jakoukoliv nekřížící se skupinu lučištníků definujme pravý okraj, což je číslo cíle, kam míří lučištník nejvíce napravo. To je zároveň nejvyšší ci skupiny.
Může se stát, že máme více stejně velkých skupin, a chceme je rozšířit o lučištníka, který stojí napravo od ostatních střelců ve skupinách. Pak upřednostňujeme skupinu s nejnižším pravým okrajem (ck nového lučištníka musí být větší, než ck ostatních).
Zaveďme posloupnost mi, i ∈{0,…,N}. Pokud si vezmeme všechny nekřížící se skupiny velikosti i, mi bude nejmenší z jejich pravý okrajů. V případě, že skupina velikosti i neexistuje, pak mi = ∞. Platí, že mi-1 ≤ mi: rozmyslete si, že ze skupiny s i střelci lze vytvořit skupinu s i-1 střelci takovou, že pravý okraj zůstane stejný. Pokud pro zadané lučištníky a jejich terče dokážeme vypočítat posloupnost mi, je maximálním počtem lučištníků nejvyšší takové i, že mi < ∞.
A jak tedy mi získat? Opět projdeme střelce zleva doprava; na začátku zvolíme m0 = -1, pro k > 0 bude mk = ∞. Pro k-tého střelce potom vylepšíme posloupnost takto: protože posloupnost mi je celou dobu neklesající, dokážeme najít takové l, že ml < ck ≤ ml+1.
Všimněte si, že přidáním k-tého lučištníka nevylepšíme mi, kde i ≤ l: pro skupiny velikosti i jsme už nalezli menší pravé okraje. Můžeme však zlepšit ml+1: představte si, že ze skupiny o l+1 lučištnících s pravým okrajem ml+1 odstraníme střelce nejvíce napravo a přidáme k-tého lučištníka – tím ml+1 snížíme, nebo necháme nezměněné. Pro i > l+1 toto udělat nemůžeme, museli bychom odstranit dva a více lučištníků a velikost skupiny by se změnila.
Ačkoliv i zde uděláme N kroků, najít správné l lze pomocí binárního vyhledávání, následně už jen upravíme ml+1. Celkový čas je tedy O(N log N).
Na závěr důležité pozorování: pokud c0, c1, …, cN zapíšeme jako posloupnost, odpovídá nalezené řešení nejdelší rostoucí podposloupnosti v ck. Není těžké převést tyto úlohy mezi sebou: ostatně většina řešitelů s plným počtem bodů si této spojitosti všimla.
Program s řešením v O(N2) (Python 3)
Program s řešením v O(N log N) (Python 3)
 29-1-6 Štítové kouzlo (Zadání)
29-1-6 Štítové kouzlo (Zadání)
Nabízí se triviální algoritmus, který vyzkouší všechny možnosti. Jenomže toto nebude fungovat vůbec rychle. Pojďme se podívat proč.
Jednotlivé kroky rozšiřování štítu můžeme zapsat do posloupnosti {L,P}n-1, kde n je počet všech hradeb. Nechť pak v této posloupnosti L reprezentuje rozšíření štítu vlevo a P rozšíření štítu vpravo. V této definici můžeme jednoduše získat počáteční úsek hradby spočítáním všech L (musíme začít dostatečně vpravo, aby rozšiřovaní vlevo mělo smysl), takto každá posloupnost jednoznačně určuje postup rozšiřování štítu.
Počet všech takových posloupností činí 2n-1. Vyzkoušení všech možností by nám tedy trvalo vždy Ω(2n) času. Jak se z toho vybrodit?
Hladové řešení nefunguje. Vybírat vždy nejvyšší úsek hradby je již vyvráceno příkladem v zadání. Stejně tak nás zradí rozšiřování směrem, kde je větší součet stojících hradeb. Ukažme si to na jednoduchém příkladu. Mějme následující hradby:
| 10 |
Zde se hladový algoritmus rozhodne rozšiřovat štít vpravo. Jenže než se dostane k nejpravějšímu úseku, oba úseky nalevo ztratí příliš mnoho hodnoty. Nakonec zachrání jen (100-5) + (10-6) + (10-7) = 102 hradeb. Kdybychom nejprve ochránili část hradeb vlevo a až potom se vydali vpravo, zachráníme jich 10 + 9 + (100-7) = 112, tedy mnohem více.
| A B C D |
| B C D E |
| B C D |
Označme Š(a,b) nejlepší možný součet výšek hradeb v úseku od a do b, který chrání náš štít v kroce k=b-a. Dále si označme V(k,i) výšku i-tého nechráněného úseku hradby v k-tém kroce, jejíž hodnota se bude rovnat max(0,h[i]-k).
Všimněme si, že Š(a,b) se rovná buďto Š(a,b-1)+V(k,b), anebo Š(a+1,b)+V(k,a), podle té z možností poskytující vyšší součet chráněných hradeb. Tedy vzorec pro Š(a,b) je max{Š(a,b-1)+V(k,b),Š(a+1,b)+V(k,a)}.
Nyní můžeme spočítat Š(0,n-1), jenž odpovídá optimálnímu rozšíření štítu nad celou hradbou. Můžeme postupovat podle definice rekurzí, kde si již spočítaná Š(a,b) zapamatujeme do tabulky, abychom je nepočítali znova.
Můžeme postupovat i jiným způsobem, a to spočítat všechna Š(a,a+k) iterativně po „vrstvách“, tedy nejprve všechna Š(a,a), potom všechna Š(a,a+1), …, až nakonec získáme hledané Š(0,n-1). Při takovém způsobu počítání nám stačí si pamatovat předchozí vrstvu, tabulka tedy není nutná.
Jestliže bychom navíc chtěli znát postup, jak jsme štít rozšiřovali, budeme si kromě Š(a,b) pamatovat i D(a,b) říkající, přidáním kterého prvku (nebo ze kterého směru) byl nejlepší štít mezi a a b rozšířen. Projitím D(0,n-1) potom získáme postup rozšiřování štítu v opačném pořadí.
Nyní stačí spočítat časovou a paměťovou složitost tohoto algoritmu. Všech dvojic a,b je O(n2), každou spočítáme nejvýše jednou. Na vypočítání každého Š(a,b) spotřebujeme konstantní čas. Celková časová složitost je tedy O(n2). Jestliže nám stačí znát pouze nejlepší součet zachráněných hradeb, vystačíme si s O(n) paměti při použití iterativní metody. Jinak je paměťová složitost shodná s časovou složitostí O(n2).
 29-1-7 Stromy kolem nás (Zadání)
29-1-7 Stromy kolem nás (Zadání)
Úkol 1: Příklady stromů
Děkujeme za pěkné příklady stromů: rodokmen (já a všichni mí biologičtí předkové), řeka se svými přítoky, adresářová struktura na disku, nebo třeba všechny možnosti, jak se může vyvíjet partie deskové hry. Přidáme k nim strukturu webových stránek (do sebe zanořené elementy HTML), programů v programovacích jazycích a nádavkem ještě vztahy mezi větnými členy či větami v souvětí. Stačí? :)
Úkol 2: Strom z postfixového výpisu
Úkol byl formulován trochu nepořádně: pokud o vrcholech stromu vůbec nic nevíme, tvar stromu se z jeho postfixového výpisu určit nedá. Pokud nám ale někdo řekne, kolik má mít který vrchol synů, už to možné je. U stromů výrazů je tato podmínka triviálně splněna: čísla jsou listy, operace mají právě dva syny. Pro jednoduchost budeme nadále předpokládat, že pracujeme se stromem výrazu.
Postfixový zápis budeme procházet zleva doprava a postupně ho překládat
na stromy: pokud jsme z 1234++* přečetli 1234+, máme zatím
hotové jednovrcholové stromy 1 a 2 a třívrcholový strom s kořenem +,
pod nímž jsou listy 3 a 4. Tyto stromy postupně slepíme do jednoho
velkého, ale z toho, co jsme zatím přečetli, dosud není jasné jak.
Budeme si tedy pamatovat nějakou posloupnost rozpracovaných stromů, říkejme jí alej. Kdykoliv ze vstupu přečteme číslo, vytvoříme jednovrcholový strom s tímto číslem a přidáme ho na konec aleje. Přečteme-li naopak nějakou operaci, odpojíme z konce aleje dva stromy, spojíme je pod nově založený kořen s danou operací a výsledek opět zapíšeme na konec aleje. Obecně objeví-li se na vstupu zápis vrcholu stupně s, spojujeme posledních s stromů z aleje.
Časová složitost tohoto algoritmu je zřejmě lineární. Kdybychom chtěli poctivě dokázat korektnost, pak třeba takto: Uvažme průběh prohledávání stromu do hloubky. Právě stojíme v nějakém vrcholu v a chystáme se ho opustit, tedy do postfixového zápisu toto v vypsat. Vrcholy na cestě z kořene do v jsme už objevili, ale na vypsání teprve čekají. Vše vlevo od této cesty jsme už vypsali, vše napravo naopak ani neobjevili.
O dekódovacím algoritmu pak platí následující invariant: při zpracování v se v aleji nachází posloupnost podstromů visících vlevo od cesty do v (v pořadí shora dolů) následovaných podstromy ležícími pod v (zleva doprava). Jakmile algoritmus uvidí v, podstromy správně poslepuje a invariant bude nadále platit.
Za odměnu vám ukážeme ještě jedno, mírně magické řešení: Postfixový zápis otočíme, čímž se z něj stane prefixový (až na opačné pořadí synů). Ten můžeme poskládat do stromu jednoduchým rekurzivním algoritmem: pokud narazíme na číslo, vytvoříme z něj jednovrcholový strom a skončíme. Pokud na operaci, dvakrát se rekurzivně zavoláme a získané dva stromy spojíme pod společný kořen. Hotovo, O(n). Formální důkaz složitosti by se vedl stejně jako u minulého algoritmu.
Úkol 3: Nejednoznačný infixový zápis
Prosté, milý Watsone: stačí uvážit zápis 1+2+3. Ten můžeme uzávorkovat
dvěma způsoby: (1+2)+3 a 1+(2+3). Pokaždé vyjde jiný strom. Prefixově
tyto stromy zapíšeme ++123 a +1+23, postfixově 12+3+
a 123++ – vše bez závorek, z předchozího úkolu už přeci víme, že nejsou třeba.
Úkol 4: Průměr stromu
Jak zadání naznačuje, k měření délky nejdelší cesty se skutečně bude hodit něco počítat během DFS. Kdykoliv se budeme vracet z podstromu s kořenem v, spočítáme dvě čísla: h(v) udávající hloubku podstromu a ℓ(v) – maximální délku cesty v podstromu.
Výpočet h(v) už známe ze zadání: v listu platí h(v)=0, ve vnitřním vrcholu se syny s1,… ,sk musí být h(v) = max(h(s1),… ,h(sk)) + 1.
Jak tedy s ℓ(v)? Rozmysleme si možné polohy vrcholu v vzhledem k této cestě:
- v je list – tehdy je celý podstrom jednovrcholový, pročež ℓ(v)=0
- v vůbec na cestě neleží – tehdy jsme cestu již započítali do některé z délek ℓ(s1) až ℓ(sk).
- v je koncovým vrcholem cesty – cesta vede z v dolů do nejvzdálenějšího listu, takže měří h(v).
- v je „zlomem“ cesty – cesta přichází zespoda z některého si a zase odchází dolů do nějakého jiného sj. První část určitě vede z listu, takže měří h(si), pak následuje hrana siv, hrana vsj a závěrečná část do listu, délky h(sj). Vrcholy si a sj samozřejmě volíme tak, abychom použili největší a druhé největší h(si).
Pro vrcholy s jedním synem může nastat druhá a třetí možnost, tedy ℓ(v) = max(ℓ(s1), h(v)+1). Je-li synů více, třetí možnost je vždy horší než čtvrtá, takže spočítáme ℓ(v) = max(ℓ(s1),… ,ℓ(sk),m1 + m2 + 2), kde m1 a m2 je první a druhé největší h(si).
Nejdelší cestu v celém stromu pak najdeme v ℓ(v) kořene.
Našimi výpočty strávíme v každém vrcholu lineární čas s počtem synů, což odpovídá složitosti samotného DFS. Celý algoritmus tedy poběží v lineárním čase.
Průměr stromu podruhé
Předveďme ještě jeden způsob, jak změřit nejdelší cestu. Strom zakořeníme v libovolném vrcholu a. Pak najdeme nejhlubší vrchol v (to už umíme jedním DFS). Tento vrchol prohlásíme za nový kořen a opět najdeme nejhlubší vrchol w. Tvrdíme, že cesta vw je jedna z nejdelších cest.
Tento algoritmus je evidentně lineární, ale není zřejmé, jestli funguje. Pojďme to dokázat sporem: předpokládejme, že existují nějaké stromy, na nichž algoritmus nefunguje. Vyberme z nich nějaký strom T s nejmenším počtem vrcholů (tomu se obvykle říká minimální protipříklad). T má alespoň 3 vrcholy – menší stromy algoritmus jistě zvládne.
Bez újmy na obecnosti můžeme předpokládat, že vrchol a není list – v opačném případě místo a vybereme jeho souseda, čímž jsme chování algoritmu nezměnili.
Nyní si všimneme, že v i w jsou listy (jinak by šlo cestu do nich ještě prodloužit). Sousedé těchto vrcholů, označme si je v' a w', listy určitě nejsou.
Proto si ze stromu T sestrojíme strom T' otrháním všech listů. V T' určitě leží vrcholy a, v' a w'. A jelikož přes listy žádné cesty nevedou, náš algoritmus spuštěný v T' z vrcholu a dojde nejprve do v' a pak do w'. Jelikož T byl minimální protipříklad, v T' musí algoritmus vydat správný výsledek, takže cesta v'w' je nejdelší.
Vezměme nyní nějakou nejdelší cestu P ve stromu T. Ta určitě vede z listu do listu, takže odtržením listů získáme nějakou cestu v T', jež jistě nemůže být delší než nejdelší cesta v'w'. Proto pro délky cest platí |P|≤ 2 + |v'w'|. Pravá strana nerovnosti je ovšem rovna délce cesty vw, takže vw je také nejdelší. Hotovo.
Úkol 5: Strážníci s drony
Mějme nějaký podstrom s kořenem v a přemýšlejme, jak může být hlídaný. Buďto k ohlídání všech jeho hran postačí strážníci, které jsme rozmístili uvnitř podstromu – tehdy mu budeme říkat samostatný. Nebo potřebujeme, aby dovnitř dronem doletěl nějaký strážník zvenku (což nutně znamená, že stojí o jednu hladinu nad v; z vyšších pozic by možná doletěl do v, ale už ne dovnitř podstromu) – tehdy hovoříme o hlídání s výpomocí.
Navíc u samostatných podstromů potřebujeme rozlišovat, jak vysoko z nich dron vyletí. Tomuto číslu budeme říkat síla hlídání a všimneme si, že se pohybuje od 0 do 2. Sílu poznáme podle toho, na jaké nejvyšší hladině se nachází strážník: strážník v kořeni (na 0. hladině) dává sílu 2, strážník na 1. hladině sílu 1, na 2. hladině sílu 0; od 3. hladiny dál nelze hlídat bez výpomoci. Navíc dodefinujeme sílu -1 pro hlídáni s výpomocí.
Nyní budeme pro každé v počítat čísla hi(v), kde i ∈{-1,0,1,2}. Budou vyjadřovat minimální cenu za ohlídání síly i. Podobně jako u hlídání bez dronů můžeme tato čísla spočítat při návratech z vrcholů, jen rozbor případů bude trochu chlupatější.
Nejprve uvažujme ohlídání síly 2. Tehdy v kořeni leží strážník (snad bychom měli říci, že stojí, ale dron se dá jistě ovládat i vleže), takže musíme započítat cenu c(v) za umístění strážníka. Podstromy ležící pod jednotlivými syny kořene pak mohou být ohlídané libovolně silně včetně síly -1. Platí tedy:
přičemž suma sčítá přes všechny syny vrcholu v.
Dobrá, snížíme sílu na 1. V kořeni jistě strážník není, ale musí být v alespoň jednom vrcholu na 1. hladině. Podstrom pod tímto vrcholem má tedy sílu 2, díky čemuž jsou ohlídány i všechny hrany mezi 0. a 1. hladinou (dron do nich doletí). Ve zbývajících podstromech zakořeněných na 1. hladině si tudíž můžeme vybrat libovolnou sílu od 0 do 2 (-1 nelze). Proto:
Počítat přímo podle tohoto vztahu by ale bylo moc pomalé: zkoušíme všechny dvojice synů a těch může být až kvadraticky mnoho. Proto si spočítáme sumu
přes všechny syny s a pak postupně zkusíme každý člen mini hi(s) odečíst a přičíst místo něj h2(s). To už jde lineárně s počtem synů.
Snižujeme dále: síla 0. Na 0. a 1. hladině nejsou strážníci, takže každá hrana mezi 0. a 1. hladinou musí být hlídaná zespoda (víme, že nevyužíváme výpomoc shora). Proto podstrom pod každým synem s musí být hlídaný silou alespoň 1. Ale nemůže to být ani víc než 1, protože pak by celková síla vyšla 1. Z toho plyne:
Konečně zbývá případ se silou -1, tedy s výpomocí shora. Všechny hrany mezi 0. a 1. hladinou jsou hlídané shora a na 0. ani 1. hladině nestojí strážníci (jinak bychom výpomoc nepotřebovali). Vrcholy na 1. hladině tedy mohou být hlídané silou 0 nebo 1. Proto:
To nám dává kompletní recept na výpočet všech hi(v) během prohledávání do hloubky. V každém vrcholu tím trávíme čas lineární s počtem synů, takže jsme DFS nezpomalili.
Teď už se stačí jen podívat na hodnoty h0, h1 a h2 v kořeni a vzít z nich minimum (h-1 neuvažujeme: už nezbývá, kdo by nám vypomohl). Uff.
Úkol 6: Excentricity
Uvažujme nějaký list ℓ a označme jeho souseda s. Nejdelší cesta z ℓ určitě vede přes s, takže excentricita ℓ je o 1 větší než excentricita s. Stačí tedy odstranit všechny listy, stanovit excentricity zbývajících vrcholů a pak dopočítat excentricity listů.
Můžeme snadno upravit algoritmus ze zadání na hledání centra stromu. Při otrhávání listů si zapisujeme, v jakém pořadí jsme je odebírali. Až nám zbude centrum, spočítáme jeho excentricitu (třeba algoritmem na výpočet hloubky stromu spuštěným v původním stromu z centra). Pak listy v opačném pořadí připojujeme zpět a dopočítáváme jim excentricity.
Všechny tři části algoritmu jistě běží v lineárním čase.