Čtvrtá série dvacátého devátého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu pošleme každému, kdo získá alespoň polovinu bodů z pěti odevzdaných úloh.
Zadání úloh
Chodbou se rozléhal hovor, smích i šustění papírů, jak se někteří studenti
ještě snažili honem rychle něco doučit. Vilém pobaveně sledoval svého
kamaráda, který rozebíral, jaké všechny otázky by v testu nechtěl potkat.
„A hlavně doufám, že se nebudou ptát na Novákovy spisky o štěstí a náhodě,“
máchl Bernard rukama.
„Tak u nich snad stačí vědět, že je postupně někdo krade z Archivu, ne?“
„Další!“ přerušil kamarády mocný hlas. Oba chlapci se usmáli a Vilém se
vydal na klasickou kontrolu před testem.
Kontrolující muž mu položil několik obvyklých otázek a začal kontrolovat
Vilémovo oblečení. „Kapesníčky?“ ujišťoval se, když pohmatem našel předmět
v kapse kalhot. Vilémovi se rozbušilo srdce, zatajil dech a jen němě přikývl.
Snad proto ho muž chvíli nejistě pozoroval, pak rázně sáhl do kapsy…
a vytáhl malou měkkou podkovu. Chvíli se tvářil zmateně, pak mu zazářily oči,
když si všiml několika čtyřlístků umně maskovaných ve vzoru Vilémovy košile.
„Čtyřlístky na zkoušku a podkova na kontrolu? Dobrej nápad, chlape,“
poplácal Viléma po zádech a čtyřlístky jeden po druhém zabavil. „Máte
štěstí, že studujete zrovna na Institutu náhodných a nápadně nenáhodných
jevů,“ dodal ještě a s úsměvem ho poslal do zkouškové místnosti.
Vilém rozhodně na čtyřlístky nespoléhal, a tak navzdory jejich zabavení
za hodinu a půl odevzdával hustě popsanou písemku. Dva zkoušející na sebe
mrkli. „Oni mají body ze semestru, že? Můžeme při odevzdání přijímat
jen písemky od lidí, kteří mají víc bodů než jejich předchůdce?“
 29-4-1 Odevzdávání písemek (10 bodů)
29-4-1 Odevzdávání písemek (10 bodů)
Studenti utvořili frontu na odevzdání písemek, každý ji odevzdá jednomu
ze dvou zkoušejících. Každý student má také nějaké body ze semestru.
Aby ale mohl student písemku odevzdat, musí mít více bodů než poslední
student, který odevzdal písemku stejnému opravujícímu; předbíhat se nesmí. Komu má kdo odevzdávat,
aby mohli odevzdat všichni?
Formálněji: je dána posloupnost celých čísel. Vaším úkolem je rozdělit ji
na dvě rostoucí podposloupnosti (případně zjistit, že to nejde).
Můžeme si představit, že každý prvek posloupnosti obarvíme jednou ze dvou
barev (třeba modrou nebo červenou). A chceme to udělat tak, aby modré prvky
tvořily rostoucí podposloupnost – tedy pokud budeme číst zleva doprava jen
modré prvky (červené přeskakujeme), budou přečtená čísla v rostoucím pořadí.
To samé musí platit pro červené prvky. Žádný prvek nemůže být obarven dvěma
barvami ani zůstat neobarvený.
Formát vstupu: Posloupnost celých čísel.
Formát výstupu: Na prvním řádku modrá podposloupnost (všechny modré
prvky čtené zleva doprava v původním pořadí), na druhém červená.
Ukázkový vstup:
9 4 14 5 17 8 26
Ukázkový výstup:
9 14 17 26
4 5 8
Ukázkový vstup:
8 1 11 12 0 6
Nezapomeňte důkladně zdůvodnit, proč vaše řešení funguje.
Řešení
Kdo ví, nakolik zkoušející jen provokovali, rozhodně se všem studentům
povedlo písemku odevzdat. Vilém si ještě zašel s Bernardem na chvíli
sednout ven a pak už hurá domů.
Následující ráno ho při pohledu do zrcadla přivítala černá plocha. „Zase? Tyhle krámy
nic nevydrží…“ povzdechl si a vyměnil baterky. Ale pořád je to asi lepší
než mít doma skleněné zrcadlo. Příběhů o strašidelných koncích už slyšel víc
než dost.
Tenhle trend začal před pár lety, když se do aut místo zpětných zrcátek začaly
instalovat zadní kamery. Tím sice neubylo dopravních nehod, ale výrazně se
zmírnily jejich následky.
Smartphony po svém příchodu zase rychle vytlačily malá osobní zrcátka, se
kterými vás dnes nepustí ani do letadla.
Jakmile dostatečně klesly ceny a spotřeba velkých LCD panelů, začala být
i velká domácí zrcadla nahrazována elektronickými. Zpočátku to byly
jednoduchoučké přístroje tvořené jen kamerou a displejem. Ale ve světě, kde
i rychlovarné konvice mají Wi-Fi, nemohla zrcadla zůstat dlouho pozadu.
Dnes jsou z nich velmi chytrá (někteří stále trvají na tom, že příliš
chytrá) a flexibilní zařízení. Nejenže si na nich ráno přečtete noviny
či prohlédnete kalendář, ale například mezi náctiletými děvčaty je velmi
oblíbená aplikace Zrcadlo, zrcadlo…
Jako každému složitějšímu zařízení, ani zrcadlům se nevyhnuly počítačové
viry a útoky. Nejčastěji v podobě šmírování kamerou, ale rozmohly se
i různé vtípky od nevinných (obraz vzhůru nohama) po celkem necitlivé
(vidíte za zády strašidelný stín či svou podobiznu digitálně zestárlou
o deset let). Ale to je malá daň za bezpečnost. V posledních měsících se
dokonce mluví o plošném zákazu skleněných zrcadel v EU…
Dost filozofování o zrcadlech, za chvíli začíná ústní zkouška! Vilém se rychle
sbalil a vyrazil.
***
Čekání na zkoušku si krátil prohlížením různých hracích automatů, které byly
rozmístěny po chodbě. Žádné výhry nevydávaly, ale studenti si na nich mohli
vyzkoušet své štěstí a různé způsoby, jak ho ovlivnit.
Jeden z automatů ho zvláště zaujal. Vypadal pro účely výzkumu štěstí až
podezřele deterministicky…
 29-4-2 Hrací automat (12 bodů)
29-4-2 Hrací automat (12 bodů)
 Na zdi visí hrací automat. Je tvořen úzkým prostorem mezi dvěma skly, do kterého
je možné z libovolného místa podél horní hrany vhodit kuličku. Ta pak padá dolů
a cestou naráží na kruhové překážky, po kterých se vždy skutálí a dál padá opět
kolmo k zemi. Nakonec dopadne na dolní hranu automatu, podél které je stupnice
udávající skóre.
Na zdi visí hrací automat. Je tvořen úzkým prostorem mezi dvěma skly, do kterého
je možné z libovolného místa podél horní hrany vhodit kuličku. Ta pak padá dolů
a cestou naráží na kruhové překážky, po kterých se vždy skutálí a dál padá opět
kolmo k zemi. Nakonec dopadne na dolní hranu automatu, podél které je stupnice
udávající skóre.
Celou situaci si můžeme představit dvojrozměrně. Plocha automatu je obdélník,
po kterém jsou nepravidelně rozmístěné překážky ve tvaru kruhu. Překážky se
nikdy nepřekrývají. Vhozená kulička je ve srovnání s těmito kruhy velmi malá,
takže si ji můžeme představit jako bod. Volným prostorem padá vždy kolmo dolů.
Pokud dopadne na kruhovou překážku, skutálí se po jejím horním okraji tak, jak
byste čekali – doleva, pokud dopadla nalevo od středu překážky, doprava, pokud
napravo.
Pro jednoduchost předpokládejte, že když kulička dopadne přesně na střed
překážky, padá vždy vpravo.
Na vstupu dostanete nejdřív popis automatu: výšku H, šířku W a počet překážek
N. Následují pro každou překážku tři čísla udávající střed a poloměr. Poté
následuje Q dotazů. Každý dotaz je popsán jedním reálným číslem udávájícím
x-ovou souřadnici místa, kde na horním okjraji automatu vhodíme kuličku. Pro
každý dotaz chceme určit x-ovou souřadnici místa na dolním okraji automatu,
kam kulička dopadne. Předpokládejte, že dotazů bude řádově alespoň tolik jako
překážek.
Řešení
Střih. Mezitím na nedaleké policejní stanici…
„Hlášení přibývá. Podivné nehody, zmizení…Včera jednoho člověka
dvakrát zasáhl blesk! Oba zásahy přežil, ale bylo to na železničním přejezdu, a
než se stačil probrat, přejel ho vlak. Kolemjdocí prý tou dobou v okolí
zahlédli černou kočku. Ale na takovouhle smůlu černá kočka nestačí…“
„Může to samozřejmě být nějaký přirozený zdroj smůly, ale kolegové
z kriminálky se domnívají, že za tímhle případem, a spoustou podobných, stojí
nějaká organizovaná zločinecká banda.“
„Dokonce dvě,“ přihodil nově příchozí policista. „Zachytili nějaké
výhružné dopisy, které si posílají mezi sebou. Máme spoustu podezřelých, ale
zatím netušíme, kdo kam patří…“
 29-4-3 Výhružné dopisy (11 bodů)
29-4-3 Výhružné dopisy (11 bodů)
Dva znepřátelené gangy si vyměňují výhružné dopisy. Oba gangy dohromady
čítají N lidí. Každý člověk patří do právě jednoho z gangů, ale nevíme
kterého. O každém člověku víme, kolik odeslal a kolik přijal výhružných
dopisů.
Rádi bychom zjistili, kdo komu posílal dopisy. To nejspíš nepůjde jednoznačně,
ale stačí nám najít jedno libovolné řešení. Jedna dvojice odesílatel-adresát si
mohla poslat více dopisů, v takovém případě nás zajímá kolik. Výhružné dopisy
se posílají pouze mezi gangy, nikdy uvnitř gangu.
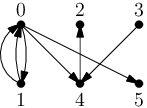
Jinými slovy, hledáme orientovaný bipartitní multigraf (tedy graf, kde mezi
jednou dvojicí vrcholů může vést více hran) – vrcholy představují lidi,
partity gangy a každá hrana jeden poslaný dopis (orientovaná od odesílatele
k příjemci). Pro každý vrchol máme předepsán jeho vstupní a výstupní stupeň
(kolik hran v něm má začínat a kolik končit). Rozdělení vrcholů na partity
není určeno, to je třeba najít. Parity mohou být různě velké.
Formát vstupu: Na prvním řádku bude přirozené číslo N udávající počet lidí (vrcholů). Dále
pro každého člověka řádek se dvěma nezápornými celými čísly udávajícími, kolik dopisů daný
člověk přijal a kolik odeslal.
Formát výstupu: Pro každou dvojici odesílatel-adresát, která si poslala
alespoň jeden dopis, vypište trojici čísel: pořadová čísla odesílatele
a adresáta (0 až N-1) a počet dopisů, které odesílatel poslal adresátovi.
Pokud existuje více řešení, vypište libovolné. Vstupy budou zadány tak, aby
vždy alespoň jedno řešení existovalo.
Ukázkový vstup:
6
2 3
1 2
1 0
0 1
2 1
1 0
Ukázkový výstup:
0 1 1
0 4 1
0 5 1
1 0 2
3 4 1
4 2 1
Odpovídající bipartitní multigraf vypadá následovně:
I v tomto případě jde jen o jedno z mnoha možných řešení.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Řešení
Do místnosti vešel starší strážník, patrně náčelník zdejší stanice. „Tak,“
odmlčel se před nepříjemnou otázkou, „kdo tady bude v pátek?“
„Já ne!“ ozval se jeden z policistů. „Viděli jste můj horoskop?“
Ostatní si vytáhli každý po jedné sirce.
Náčelník přešel do vedlejší místnosti, kde mezitím pokračovala přestavba místní počítačové sítě. Byla
tam spousta počítačů, switchů, routerů a mezi nimi čím dál více kabelů.
„Pozor kabel!“ zavolal jeden z instalujících.
„Na co tu máme víc počítačů než celý útvar informační bezpečnosti? O ty kabely
se brzo někdo přerazí…“
„Evropská unie,“ odvětil montér, nepřestávaje
tahat kabely. „Pokud neutratíme všechno, musíme dotaci vrátit. Ale
oficiálně – jako zálohu pro případ výpadku.“
 29-4-4 Policejní síť (8 bodů)
29-4-4 Policejní síť (8 bodů)
Policejní síť tvoří N počítačů, každý může být propojen s několika dalšími.
Síť tvoří strom.
Navíc máme určeno K důležitých počítačů (vrcholů). Ty
chceme spárovat do dvojic, které se budou navzájem zálohovat: pokud jeden
počítač z dané dvojice přestane fungovat, zastoupí jeho činnost ten druhý.
Aby to bylo možné, musí si počítače ve dvojici průběžně navzájem předávat
všechna svá data – ta tečou po cestě, která dané dva vrcholy ve stromu
spojuje (říkejme jí spojení).
Není určeno, který počítač máme spárovat s kterým, můžeme si vybrat libovolně.
Ale protože nakoupené počítače přes svou cenu nejsou příliš výkonné, nechceme,
aby jakýmkoli počítačem procházelo víc než jedno spojení.
Tedy hledáme takové rozdělení důležitých vrcholů do dvojic, aby cesty spojující
vrcholy v každé dvojici byly navzájem disjunktní – neměly žádné společné
vrcholy ani hrany.
Pokud existuje více možných řešení, vypište všechna.
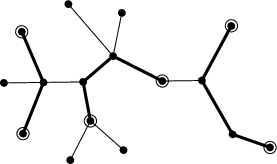
Na následujícím obrázku je příklad takového stromu. Důležité vrcholy (dostanete
na vstupu) jsou označeny kroužkem. Nalezená spojení (výstup algoritmu) jsou
zvýrazněná tučně. V tomto případě existuje jediné řešení.
Ale pro následující zadání žádné řešení neexistuje:
Řešení
Ráno se Vilémovi povedlo při vypínání budíku spadnout z postele
a v koupelně si málem zlomil nohu. Když mu jeho chytré zrcadlo
s kalendářem prozradilo, že je čtvrtek 12., raději nepřemýšlel
o tom, jak zlý bude příští den, a rozhodl se doplnit zásoby.
Jelikož nemohl najít oblíbenou tašku, vzal si prostě svůj běžný batoh
a přihodil raději pár talismanů. Jim navzdory ho málem praštily vchodové
dveře. Ještě že na ulici nebylo moc lidí, takže si netrhl takovou ostudu.
Neprošel ani celou ulicí, když se mu rozvázala tkanička, on o ni zakopl
a při pádu hodil klíče do kanálu. Tehdy ho dostihla děsivá myšlenka.
Jeho středeční zkouška byla předevčírem, přesto jeho zrcadlo včera
tvrdilo, že je středa, a to znamená… že je pátek třináctého!
Na chvíli ho popadl vztek. Dávno bylo schváleno, že ten den budou vždy
od časného rána do večera znít sirény, a zatím ticho. Holt byly sirény
asi rozbité, jako obvykle. Vztek ale vystřídala zvědavost. Kdo je tedy
těch pár lidí, kteří si troufli vyjít ven?
V té chvíli se ovšem jeden z těch lidí vydal právě k Vilémovi.
„Co tu sakra vyvádíš? Vy nováčci 'ste pořád větší amatéři!“ nadával,
popadl Viléma a vlekl ho ulicí. Vilémovi se hlavou honily myšlenky a moc
nestíhal vnímat cestu. Najednou byli před jakousi budovou, najednou se
v ní proplétali různými neznačenými schodišti a východy… a najednou
byli na místě. Mohli být vážně ve třináctém patře?
Vilém se opatrně rozhlédl kolem sebe. Jeho pozornost upoutala zejména
knihovna u zdi. Byly v ní vyskládané různé knihy a sešítky a… to
snad nebylo možné! Novákovy spisky o štěstí a náhodě. Mohly všechny
ukradené kopie z Archivu dokumentů o mezipřirozenosti zmizet sem?
 29-4-5 Chybějící spisek (12 bodů)
29-4-5 Chybějící spisek (12 bodů)
Z Archivu dokumentů o mezipřirozenosti bylo postupně ukradeno mnoho
očíslovaných spisků. Vilém nyní M těchto spisků vidí v knihovně
v tajné skrýši a zajímalo by ho, jaké nejmenší číslo spisku tu chybí.
Protože ale v místnosti není sám, nemůže spisky jen tak přerovnávat,
stejně tak si nemůže prostě vytáhnout papír a tužku a psát si poznámky.
Musí si vystačit s omezeným množstvím paměti poskytnutým vlastní hlavou…
Formálněji: v paměti máte k dispozici nesetříděnou posloupnost N čísel. Tato
část paměti je jen pro čtení, to zejména znamená, že si posloupnost nemůžete
setřídit. Dále máte k dispozici konstantní množství pomocné paměti. Určete
nejmenší přirozené číslo, které se v posloupnosti nevyskytuje.
Ukázkový vstup:
3 0 9 8 6 1
Řešení
Něco Viléma vrátilo do přítomnosti, upoutalo jeho pozornost zpátky do
místnosti. Mezitím se tu nahromadilo dost lidí, a ti všichni teď umlkli
a pozorovali přicházejícího muže.
Vilém si nebyl jistý, jestli ho víc znepokojuje černá kočka v mužově
náručí, nebo fakt, že nikoho jiného tato maličkost zjevně netrápí.
„Jsem rád, že vás tu všechny zase vidím,“ ujal se muž slova.
„Jak jistě víte, černá kočka je ideálním prostředkem k neutralizaci
nežádoucích osob. Výsledek nejenže vypadá jako nehoda, ona to doopravdy
je nehoda.
Musíte správně odhadnout počet. Jedna obvykle nestačí, ale pokud jich
použijete příliš,“ pohlédl přísně na jednoho z přítomných,
„jsou druhý den noviny plné zpráv o zásazích blesku na železničním přejezdu.
Jenže i když se trefíte, občas někdo kočku zahlédne…
Proto jsem vážně rád, že se nám tehdy povedlo zfalšovat utracení
téhle krásky,“ zdvihl kočku spočívající mu v náručí. „Určitě si vzpomínáte, jak byla vláda nesvá z černé kočky,
která nenosí smůlu, ale nejspíš ani oni nevěděli, jak silnou mají
v ruce zbraň.“
„Naši výzkumníci se ovšem pustili do práce a zjistili…,“ muž se
zamyšleně zamračil, pak mávl rukou, „nějakou genovou odlišnost.
A protože tu od nás mají skvělé vybavení a jsou šikovní, dovolte mi
představit vám,“ dramaticky se otočil a ukázal k přicházející hnědé
kočce.
Obezřetně k ní došel, opatrně ji vzal do náruče a pak si z přihlížejících
vyvolal jednoho neochotného dobrovolníka. O pár spadlých předmětů, vylitých
skleniček, zakopnutí a dalších pozoruhodných náhod později začínalo být
jasné, jak mocnou zbraň má skupina k dispozici.
„Hele, a proč vlastně nenabarvíme nějakou černou kočku?“ zeptal se
tiše někdo poblíž Viléma.
„Nepamatuješ si snad, co se stalo Dlouhánovi, když se o to pokusil?“
odpověděl hned jiný a pak byl klid, dokud se slova opět neujal šéf.
„Věřím, že s naším novým miláčkem se nám bude dobře dařit a pěkně se
rozrosteme. Proto si taky už brzy pořídíme nové sídlo, hned jak vymyslíme,
jak velký pozemek vlastně chceme koupit.“
 29-4-6 Nové sídlo (11 bodů)
29-4-6 Nové sídlo (11 bodů)
Zločinecká organizace si chce postavit nové sídlo. To má půdorys ve
tvaru konvexního mnohoúhelníku. Ráda by koupila nejmenší možný
obdélníkový pozemek, na který se budova vejde. Ve městě jsou pozemky drahé
a jiný než obdélníkový vám neprodají. Zároveň by ale chtěla, aby budova
alespoň jednou stranou přiléhala k ulici (tedy k okraji pozemku).
Formálně: je dán konvexní mnohoúhelník. Najděte (obsahem) nejmenší obdélník, do
kterého se mnohoúhelník celý vejde. Obdélník může být v obecné poloze
(libovolně natočený), ale chceme, aby alespoň jedna strana mnohoúhelníku
přiléhala ke straně opsaného obdélníku.
Formát vstupu: Počet vrcholů mnohoúhelníka N a souřadnice jeho
vrcholů v pořadí na obvodu. Můžete předpokládat, že souřadnice jsou
celočíselné.
Formát výstupu: Jedno reálné číslo udávající obsah nejmenšího opsaného
obdélníku splňujícího popsaná kritéria.
Ukázkový vstup:
5
0 0
6 2
6 4
2 4
0 2
Řešení
Tohle je zlé…
Vilém tušil, že by měl něco udělat, ale neměl ponětí co. Zavolat policii zřejmě
nepomůže. Dnes si nikdo zasáhnout netroufne. I kdyby troufl, nejspíš by to
skončilo fiaskem.
V zoufalství prohrábl kapsy. Zalaminovaný čtyřlístek měl jeden list ulomený.
Pochopitelně.
Krom jiného vytáhl i malé klubíčko vlněné příze, kterým občas bavíval své
domácí kočky. Teprve při pohledu na něj si pořádně uvědomil, že nebezpečná
kočka nosící smůlu je pořád kočka. A kočky si rády hrají.
Pár metrů odmotal, zbytek zajistil uzlem a hodil
směrem k hnědé kočce. Plán byl jednoduchý: upoutat její
pozornost, přitáhnout klubíčko zpět a s trochou štěstí (ehm) ji tím přilákat.
Ale přece byste nečekali, že v pátek třináctého nějaký plán vyjde.
Zhruba ve stejnou chvíli se staly dvě věci: šéf se ohlédl Vilémovým směrem a
provázek se přetrhl. Kočka viděla klubíčko dopadnout asi metr před sebe.
Najednou pocítila zvlášní nutkání líně odhlédnout a odejít, které přicházelo
zdánlivě odnikud.
Ale sama měla jiný názor. Tady se objevil zajímavý předmět, který chce
prozkoumat, a pokud si vesmír myslí, že by měla znuděně odejít, tak si vesmír
může s prominutím trhnout.
Neslyšně se připlížila ke klubíčku a párkrát do něj šťouchla packou. Vždy se
o kus pohnulo a skutálelo zpátky.
„Co tam blbneš? Nehraj si a dávej pozor!“ adresoval nevrle šéf Vilémovi.
Ono se to nehýbe! Asi spí… Kočka se napřáhla a prudce vymrštila směrem
ke klubíčku, odrážejíc ho o několik metrů kupředu. Wihíí!
Šéf, nezpozorovav toto dění, se pomalu rozešel směrem k Vilémovi právě ve
chvíli, kdy kočka vyběhla za klubíčkem — a zkřížila tím šéfovi cestu.
***
Na policejní stanici byl toho dne klid. Seděl tu jediný strážník, který si
vytáhl kratší sirku, a pozorně si prohlížel protější zeď. Raději si netroufl
ani číst noviny.
Když tu z ničeho nic do služebny zmateně vběhl vyděšený muž. Vypadal, jako
by spatřil nějaký přízrak, a pravděpodobně netušil, kde se nachází. Proběhl
kanceláří bez ohlédnutí otevřenými dveřmi do sousední místnosti…
kde zakopl o jeden z nově natažených síťových kabelů.
Při pádu mu vypadla spousta schémat a náčrtků popisujících plány jeho
zločinecké organizace, poznámky o genetice černých koček, seznamy likvidovaných
osob. Strážník k němu opatrně přišel a papíry prolistoval.
„Kdopak se to chytil – do naší sítě?“ nemohl si odpustit úšklebnou poznámku.
„Z toho si nic nedělejte, tohle se tu stává pravidelně. V pátek třináctého
zločince nechytáme. Nejenže to není bezpečné, ale hlavně to není potřeba. Přichází
sami…“
Nepodceňujte kočky.
Příběh pro vás přichystali
Karry Burešová & Filip Štědronský
 29-4-7 Rozebíráme stromy (15 bodů)
29-4-7 Rozebíráme stromy (15 bodů)
Vítejte u dalšího dílu stromového seriálu. Tentokrát se zaměříme
na cestové operace. Tím myslíme takové, které dostanou dva
vrcholy stromu a mají něco provést s cestou mezi nimi. Třeba
zjistit, jak je tato cesta dlouhá, nebo najít na ní hranu s největším
ohodnocením.
Pro mělké stromy je to snadné: hledáme-li cestu mezi vrcholy
x a y, stačí z obou vrcholů stoupat směrem ke kořeni, až se
obě cesty poprvé protnou v nejbližším společném předchůdci p (to jsme prozkoumali v minulém dílu).
Hledanou cestu pak můžeme poskládat ze dvou částí: cesty mezi x a p
a cesty mezi y a p. Vše zvládneme v čase lineárním s hloubkou stromu.
Snadné to je i pro stromy, které se vůbec nevětví, tedy samy mají tvar
cesty. V druhém dílu jsme se naučili přimět intervalové
stromy, aby v logaritmickém čase vyhodnocovaly dotazy na libovolné intervaly
posloupnosti. Můzeme si tedy pořídit intervalový strom pro posloupnost
hran na cestě a intervaly pak budou odpovídat jejím podcestám. Dokonce pomocí
líného vyhodnocování zvládneme rychle měnit ohodnocení hran na podcestě.
V tomto dílu si ukážeme, jak tyto dvě techniky spojit. Zavedeme takzvanou
dekompozici stromu na lehké a těžké hrany neboli heavy-light
dekompozici. Ta nám pomůže k rychlému vyhodnocování cestových
dotazů v libovolně hlubokém a libovolně košatém stromu. Jen se nám strom
nebude smět pod rukama měnit, tedy až na ohodnocení vrcholů a hran.
Heavy-light dekompozice (HLD)
Nejprve pár definic.
Mějme nějaký zakořeněný strom. Označíme T(v) podstrom složený z vrcholu v
a všech jeho (i nepřímých) potomků. Velikostí podstromu míníme počet jeho
vrcholů a budeme ji značit size(v).
Hrany z každého vrcholu do jeho synů rozdělíme na lehké a těžké následovně:
hranu do největšího podstromu prohlásíme za těžkou, všechny ostatní za lehké.
Existuje-li více největších podstromů, vybereme si libovolný jeden z nich.
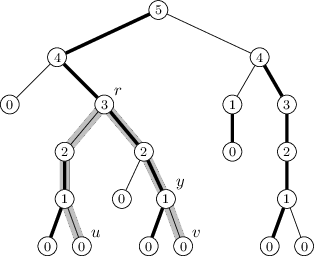
Jak to dopadne pro jeden konkrétní strom, vidíme na následujícím obrázku.
Čísla ve vrcholech jsou jejich size.
Těžké hrany jsou na obrázku vyznačeny tučně a zjevně tvoří cesty. To není
náhoda, platí to v každém stromu. Stačí si uvědomit, že z každého vrcholu
může vést dolů nejvýše jedna těžká hrana. (Dokonce víme, že není-li vrchol
list, vede z něj právě jedna taková.)
Navíc platí, že lehkých hran není nikdy mnoho za sebou. Přesněji řečeno,
na cestě z kořene do libovolného vrcholu v leží nejvýše log2 n lehkých
hran (n jako obvykle značí velikost celého stromu).
Pojďme to dokázat. Vydejme se z kořene do v a sledujme, jak se mění size
aktuálního vrcholu. Za chvíli uvidíme, že kdykoliv projdeme po lehké hraně,
klesne size aspoň dvakrát. Po k lehkých hranách tedy klesne aspoň 2k-krát,
takže kdyby bylo k > log2 n, nezbyly by v podstromu žádné vrcholy.
Dobrá, proč tedy na lehké hraně size tolik klesá? Uvažme lehkou hranu
z nějakého vrcholu u do jeho syna ℓ. Z definice musí existovat i těžká
hrana do jiného syna t a platí size(t) ≥ size(ℓ). Jenže podstromy
T(ℓ) a T(t) jsou součástí T(u), takže size(u) > size(t) + size(ℓ)
a z toho ihned size(u) > 2size(ℓ).
Pojďme zopakovat, co jsme zjistili:
- Heavy-light dekompozice rozkládá strom na těžké cesty, které jsou
propojené lehkými hranami.
- Každý vrchol leží na právě jedné těžké cestě. (Tedy připustíme-li i cesty
složené z jediného vrcholu.)
- Každá lehká hrana vede z vrcholu nějaké těžké cesty do nejvyššího vrcholu jiné
těžké cesty.
- „Lehká hloubka“ je logaritmická. Přesněji řečeno, mezi každými dvěma
těžkými cestami leží O(log n) lehkých hran.
Úkol 1 [2b]
Někdy se používá jiná definice těžkých hran: hrana z vrcholu v do syna s
je těžká, pokud size(s) > size(v)/2. Rozmyslete, jak se takto definovaná
dekompozice bude lišit od té naší. Překreslete podle toho předchozí obrázek.
Dekompozici si můžeme představit i tak, že každou těžkou cestu zkontrahujeme do jediného
vrcholu. Tím dostaneme jiný strom, v němž zbudou jen původní lehké hrany a bude logaritmicky
hluboký. Jak vypadá, je vidět na následujícím obrázku. Vrcholy bez písmenek odpovídají
triviálním (jednovrcholovým) těžkým cestám.
Výpočet dekompozice
Nyní se podíváme, jak HLD reprezentovat v paměti a zejména jak ji rychle sestrojit.
V každém vrcholu v našeho stromu si budeme pamatovat:
- size(v) – velikost podstromu pod v
- hson(v) – do kterého syna vede těžká hrana (nebo ∅, pokud žádný není,
což je možné jen tehdy, je-li v list)
- path(v) – odkaz na těžkou cestu, na níž vrchol leží
- index(v) – kolikátý v pořadí na těžké cestě je (číslujeme od nuly od spodního vrcholu cesty)
Těžké cesty si pamatujeme bokem. Pro cestu p uložíme:
- lparent(p) – otec kořene cesty (tak budeme říkat jejímu nejvyššímu vrcholu,
tedy vrcholu s nejvyšším indexem); tedy vrchol, z nějž vede do kořene lehká hrana.
Může být ∅, pokud je kořen cesty také kořenem celého stromu.
- plen(p) – délka cesty (počet hran na ní)
- pvertex(p) – pole vrcholů cesty v pořadí jejich indexů
 Dekompozici můžeme snadno spočítat dvojím prohledáním do hloubky. Při
tom prvním stanovíme velikosti podstromů, rozhodneme, které hrany jsou lehké
a těžké, a vypočteme indexy. Druhé sestrojí popisy jednotlivých těžkých
cest.
Dekompozici můžeme snadno spočítat dvojím prohledáním do hloubky. Při
tom prvním stanovíme velikosti podstromů, rozhodneme, které hrany jsou lehké
a těžké, a vypočteme indexy. Druhé sestrojí popisy jednotlivých těžkých
cest.
První prohledání vypadá následovně. Spouštíme ho v kořeni stromu a při
návratu z rekurze počítá jednotlivé vlastnosti vrcholů podle definice.
- HLD1(v):
- size(v) ←1
- h ←∅ ◁ kam povede těžká hrana?
- Pro všechny syny s vrcholu v:
- HLD1(s)
- size(v) ←size(v) + size(s)
- Pokud h=∅ nebo size(s) > size(h):
- h ←s
- hson(v) ←h
- Pokud h=∅: ◁ jsme v listu
- path(v) ←nová těžká cesta
- index(v) ←0
- Jinak: ◁ pokračování těžké cesty
- path(v) ←path(h)
- index(v) ←index(h) + 1
Druhé prohledávání spouštíme opět z kořene. Jako druhý parametr předáváme
otce aktuálního vrcholu, pro kořen je to ∅. Vždy posbíráme vrcholy
na jedné těžké cestě a pak se zavoláme na všechny jejich syny.
- HLD2(v,o):
- p ←path(v) ◁ vrchol v je kořenem těžké cesty p
- lparent(p) ←o
- plen(p) ←index(v)
- pvertex(p) ←nové pole délky plen(p)+1
- Dokud v≠ ∅: ◁ procházíme těžkou cestu
- pvertex(p)[index(v)] ←v
- Pro všechny syny s vrcholu v:
- HLD2(s,v) ◁ při tom rekurze na syny
- v ←hson(v) ◁ pokračujeme po těžké cestě
Obě prohledání provedou konstantní množství práce pro každý vrchol
a hranu stromu, celkem tedy O(n). Dodejme, že by se všechno dalo
zvládnout během jediného DFS, ale ve dvou nám to přijde přehlednější.
Stromoví předchůdci
Abychom si osahali, jak se s HLD zachází, zkusíme ji použít na úlohu
hledání nejbližšího společného předchůdce z minulého dílu.
Vzpomeňme si na primitivní algoritmus, který z každého ze zadaných
vrcholů prošel po cestě do kořene, značkoval vrcholy a číhal, kde se
obě cesty poprvé potkají. Teď na to půjdeme podobně, ale místo jednotlivých
vrcholů budeme značkovat najednou celé těžké cesty.
Pojmenujme zadané vrcholy u a v. Nejprve budeme stoupat z u ke kořeni.
Kdykoliv jsme v nějakém vrcholu x, z path(x) se dozvíme, na které
těžké cestě p se nacházíme. Pak hned vyskočíme z kořene těžké cesty
po lehké hraně do vrcholu lparent(p). Ještě si k těžké cestě poznačíme
novou položku enter(p) říkající, kudy jsme na cestu vstoupili.
Nenavštívené cesty budou mít enter(p)=∅.
Poté budeme stoupat z v. Stejným způsobem, ale místo značení těžkých
cest budeme naopak testovat, zda už nejsou označené. Dříve či později
narazíme na těžkou cestu p, na níž jsme už byli při stoupání z u.
Přitom víme, kudy jsme se na tuto cestu v obou případech napojili –
v jednom místě napojení teď stojíme, druhé máme uložené v enter(p).
Hledaným společným předchůdcem je vyšší z těchto dvou míst, což poznáme
podle indexů vrcholů.
V pseudokódu to vypadá takto:
- lca(u,v):
- x ←u ◁ z u do kořene
- Dokud x≠ ∅, opakujeme:
- p ←path(x)
- enter(p) ←x
- x ←lparent(p)
- y ←v ◁ z v do kořene
- Dokud enter(path(y)) =∅, opakujeme:
- y ←lparent(path(y))
- r ←enter(path(y)) ◁ místa napojení: r a y
- Dokud u≠ ∅, opakujeme: ◁ smažeme značky
- enter(path(u)) ←∅
- u ←lparent(path(u))
- Pokud index(y) > index(r): ◁ vrátíme vyšší z r a y
- Vrátíme y.
- Jinak:
- Vrátíme r.
Průběh algoritmu můžeme sledovat na následujícím obrázku. Čísla ve vrcholech
jsou jejich indexy, tučně jsou zvýrazněny těžké cesty, šedivě je podbarvena
cesta mezi u a v.
Časová složitost funkce lca je O(log n), neboť při každém stoupání
navštíví nejvýše logaritmicky těžkých cest a každou z nich zpracuje v konstantním
čase. Získali jsme tedy datovou strukturu pro společné předchůdce, které
stačí předvýpočet v čase O(n) a odpovídá na dotazy v O(log n).
Úkol 2 [3b]
Navrhněte algoritmus, který bude pomocí HLD odpovídat
na dotazy na vzdálenost zadaných dvou vrcholů (tedy počet hran
na cestě mezi nimi).
Kudy, kudy cestička?
Nyní se podíváme na to, jak pomocí HLD odpovídat na cestové dotazy.
Předvedeme si to na příkladu cestových minim. Dostaneme zadaný strom,
jehož hrany budou ohodnoceny celočíselnými cenami. Pak nám budou
přicházet dotazy na nejlevnější hranu na cestě mezi zadanými vrcholy.
Pro strom si opět spočítáme HLD a každou těžkou cestu navíc opatříme
intervalovým stromem, který bude umět odpovídat na intervalová minima cen
na této cestě. Ceny těžkých hran si tedy budeme pamatovat v intervalových
stromech, zatímco ceny lehkých hran uložíme samostatně. Jeden intervalový strom
vybudujeme v čase lineárním v délce jeho těžké cesty a jelikož každý vrchol
leží na právě jedné těžké cestě, sestrojíme celou datovou strukturu v čase O(n).
Nyní přijde dotaz na cestu mezi nějakými vrcholy u a v. Spustíme algoritmus
pro lca(u,v) a během výpočtu si zapamatujeme, kterými lehkými hranami
a kterými částmi těžkých cest jsme prošli. Pak stačí najít nejlevnější z těchto
lehkých hran a minim částí těžkých cest. Lehkých hran je O(log n) a každou
zpracujeme v konstantním čase, těžkých cest je také O(log n) a na každé
provádíme intervalový dotaz v čase O(log n). Dohromady tedy strávíme čas
O(log 2 n).
Podobně můžeme provádět cestový update. Pořídíme si intervalové stromy
s líným vyhodnocováním, které dovedou intervalový update v logaritmickém čase.
Kdykoliv třeba budeme chtít zdražit všechny hrany na nějaké cestě o δ,
rozložíme update na zdražení O(log n) lehkých hran a O(log n)
intervalových updatů částí těžkých cest v jejich intervalových stromech.
Vše opět stihneme v čase O(log 2 n).
Úkol 3 [5b]
Zrychlete cestový dotaz na O(log n) za předpokladu, že ceny hran se
od inicializace struktury již nezmění. Inicializace by měla stále pracovat
v lineárním čase.
Úkol 4 [5b]
Mějme graf s ohodnocenými hranami a jeho minimální kostru.
Pro každou hranu, která neleží v kostře, spočítejte, o kolik nejvýše můžeme její ohodnocení
snížit, aby kostra stále zůstala minimální.
Martin „Medvěd“ Mareš
Řešení
 29-4-1 Odevzdávání písemek (10 bodů)
29-4-1 Odevzdávání písemek (10 bodů) Na zdi visí hrací automat. Je tvořen úzkým prostorem mezi dvěma skly, do kterého
je možné z libovolného místa podél horní hrany vhodit kuličku. Ta pak padá dolů
a cestou naráží na kruhové překážky, po kterých se vždy skutálí a dál padá opět
kolmo k zemi. Nakonec dopadne na dolní hranu automatu, podél které je stupnice
udávající skóre.
Na zdi visí hrací automat. Je tvořen úzkým prostorem mezi dvěma skly, do kterého
je možné z libovolného místa podél horní hrany vhodit kuličku. Ta pak padá dolů
a cestou naráží na kruhové překážky, po kterých se vždy skutálí a dál padá opět
kolmo k zemi. Nakonec dopadne na dolní hranu automatu, podél které je stupnice
udávající skóre.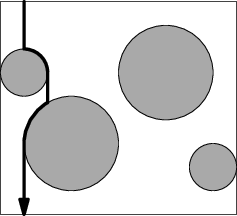
 29-4-3 Výhružné dopisy (11 bodů)
29-4-3 Výhružné dopisy (11 bodů)




 29-4-7 Rozebíráme stromy (15 bodů)
29-4-7 Rozebíráme stromy (15 bodů)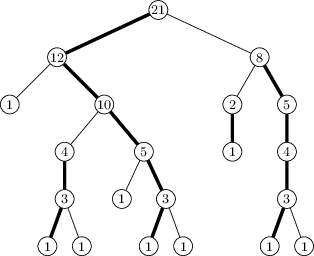

 Dekompozici můžeme snadno spočítat dvojím prohledáním do hloubky. Při
tom prvním stanovíme velikosti podstromů, rozhodneme, které hrany jsou lehké
a těžké, a vypočteme indexy. Druhé sestrojí popisy jednotlivých těžkých
cest.
Dekompozici můžeme snadno spočítat dvojím prohledáním do hloubky. Při
tom prvním stanovíme velikosti podstromů, rozhodneme, které hrany jsou lehké
a těžké, a vypočteme indexy. Druhé sestrojí popisy jednotlivých těžkých
cest.