Pátá série třicátého prvního ročníku KSP
Celý leták v PDF.
Dostává se k vám řešení poslední série hlavní kategorie letošního ročníku. Ještě, než vás pohltí letní radovánky se tak můžete podívat na to, jak jsme které úlohy zamýšleli my organizátoři – třeba se z toho můžete naučit nějaké nové triky.
Dále dodáváme, že stejně jako předchozí série je i řešení této rozděleno na dvě části: na samotná autorská řešení, která vydáváme brzy po termínu série, a na komentáře k došlým řešením, která vydáváme až po opravení vašich řešení.
Pokud se vám cokoliv nezdá nebo máte nějaký dotaz, neváhejte se ozvat na našem fóru nebo emailem na známou adresu.
Řešení úloh
- 31-5-1: Písmenková polévka
- 31-5-2: Rozinky a mandle
- 31-5-3: Kváskový chléb
- 31-5-4: Otesánek ve vývařovně
- 31-5-5: Přísady na pizze
 31-5-1 Písmenková polévka (Zadání) (Komentáře)
31-5-1 Písmenková polévka (Zadání) (Komentáře)
Kdykoliv máme nějakou permutaci σ na {1,… ,n}, můžeme ji provést dvakrát po sobě a tím získat permutaci σ2, které se opravdu říká druhá mocnina permutace σ.
Jednodušší verze úlohy po nás chce, abychom zjistili, zda pro danou permutaci π existuje permutace σ taková, že σ2 = π. Jinými slovy máme najít druhou odmocninu z permutace π. Ve složitější verzi máme zjistit, kolik takových druhých odmocnin existuje, ale to ještě na chvíli odložme.
Anatomie druhých mocnin
Zamyslíme se nad tím, jak mohou vypadat druhé mocniny permutací. K tomu se hodí představit si graf permutace σ: jeho vrcholy jsou prvky 1,… ,n a orientovaná hrana vede z i do j právě tehdy, když permutace pošle prvek i do prvku j. Z každého vrcholu vede právě jedna hrana a také do něj právě jedna hrana přichází. Proto musí všechny komponenty souvislosti grafu mít tvar orientované kružnice.
Graf permutace σ2 získáme jednoduše: množinu vrcholů má stejnou, hrany vzniknou z dvojic na sebe navazujících hran v původním grafu (to ukazujeme už na obrázku v zadání). Jednotlivé kružnice v grafu spolu evidentně neinteragují, takže si stačí rozmyslet, jak vypadá druhá mocnina kružnice (jelikož je to také permutace, musí být zase složená z jedné nebo více kružnic).
Očíslujme vrcholy kružnice v0,… ,vk-1. Pokud je k liché, povede v druhé mocnině kružnice z v0 do v2, v4, …, vk-1, v1, v3, …, vk-2 a zpět do v0 – všechny vrcholy tedy opět tvoří kružnici, jen v jiném pořadí. Jinak je to pro sudé k: z v0 se dostaneme do v2, v4, …, vk-2 a zpět do v0. To je kružnice poloviční délky; podobně z v1 se projdeme po druhé kružnici poloviční délky.
Dokázali jsme tedy, že druhá mocnina liché kružnice je stejně dlouhá kružnice, zatímco sudá kružnice se umocněním rozpadne na dvě kružnice poloviční délky.
Existence odmocniny
Vraťme se k původní otázce: pro permutaci π hledáme σ takovou, že π=σ2. Už víme, že každý cyklus v π musel vzniknout z nějakého cyklu v σ: buďto přeskládáním stejně dlouhého (to jde jen pro liché cykly), nebo rozpůlením cyklu dvojnásobné délky (to jde pro liché i pro sudé).
Pro všechny liché cykly zvolíme přeskládání, protože to funguje vždy. Sudé cykly budeme muset získat půlením, což ovšem znamená, že jich od každé délky musí existovat sudý počet.
To nám dává jednoduchý test existence odmocniny: Permutaci π rozložíme na cykly. Spočítáme, kolik cyklů existuje od každé délky. Pak stačí zkontrolovat, že od každé sudé délky máme sudý počet cyklů.
Nalezení odmocniny je také snadné: každý lichý cyklus naskládáme „napřeskáčku“, sudé cykly budeme brát po dvojicích stejné délky a každou dvojici „sezipujeme“ dohromady. Vše jistě stihneme v lineárním čase.
Počet odmocnin
 Nyní se pustíme do těžší verze úlohy: kolik je druhých odmocnin?
K tomu postačí jednoduchá kombinatorika.
Nyní se pustíme do těžší verze úlohy: kolik je druhých odmocnin?
K tomu postačí jednoduchá kombinatorika.
Jelikož kružnice různých délek spolu při odmocňování neinteragují, stačí počet odmocnin zjistit pro každou délku zvlášť a pak výsledky vynásobit.
Nechť máme t kružnic délky k. Nejprve uvažme případ, kdy k je sudé. Tehdy musí být t také sudé (jinak neexistuje žádná odmocnina). Kružnice musíme spárovat a každý pár sezipovat.
- Spočítáme možná párování. Popíšeme proces, který párování vytváří, a všimneme si, že ke každému párování dojde právě jedním způsobem. Kružnice očíslujeme od 1 do t. Vždy vezmeme dosud nespárovanou kružnici s nejmenším číslem a vybereme, s čím ji spárujeme. Pro první pár máme t-1 možností, pro druhý t-3 možností, a tak dále, až poslední pár je jednoznačně tvořen dvěma zbylými kružnicemi. Máme tedy (t-1)·(t-3)·(t-5)·… ·3·1 možných párování.
- V každém páru můžeme při zipování kružnice navzájem otočit. To jde udělat celkem k způsoby, pro všechny páry tedy kt/2 způsoby.
Pro sudé k tedy existuje celkem (t-1)·(t-3)·… ·1·kt/2 odmocnin.
| ( | t | ) |
| p |
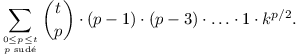
Od vzorečku k algoritmu
Náš vzoreček jde jistě naprogramovat v polynomiálním čase, ale my se nespokojíme s ničím pomalejším než lineárním. Čtenář to snad ocení, nebo aspoň přeskočí :-)
Nejprve si rozmyslíme, jak rychle spočítat kombinační číslo. Z definice víme:
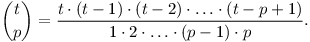
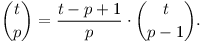
Celou sumu tedy spočteme v čase O(t). Případ se sudým k v tomto čase jistě také stihneme. Jelikož součet všech délek kružnic činí nejvýše n, výpočty pro všechny délky dohromady potrvají O(n).
 31-5-2 Rozinky a mandle (Zadání)
31-5-2 Rozinky a mandle (Zadání)
Nejdříve si rozmysleme, jak ověřit, zda umíme najít rozinkový K-úhelník pro nějaké konkrétní K. Aby nám to vůbec mohlo vyjít, K musí zřejmě dělit N bez zbytku (jinak by nemohly být všechny strany stejně dlouhé).
Mnohoúhelník je jednoznačně určen hodnotou K a jedním vrcholem. Každý další vrchol je vždy N/K důlků od předchozího. V každém souvislém úseku důlků délky N/K je právě jeden vrchol našeho pravidelného mnohoúhelníku. Můžeme si tedy zvolit libovolný takový úsek a pro každý z důlků v něm ověřit, jestli může být vrcholem rozinkového mnohoúhelníku. Stačí se podívat na K důlků pro každý potenciální vrchol a zkontrolovat, že obsahují rozinky.
Zkoušíme N/K mnohoúhelníků, pro každý kontrolujeme K důlků, tedy se celkem podíváme nejhůře do K·N/K = N důlků, každý kontrolujeme maximálně jednou. Ověřit, že mnohoúhelník existuje pro dané K, tedy umíme v čase O(N).
Pokud bychom vyzkoušeli všechny možné hodnoty K od 3 do N, tak nám to vše zabere čas O(N2). Jak jsme si už ale všimli, K musí být dělitelem čísla N.
Kolik takových dělitelů je? Dělitele můžeme spárovat do dvojic – dělitel d bude ve dvojici s N/d (to je určitě také dělitel N). V každé dvojici je určitě jeden dělitel menší nebo rovný √N a jeden větší nebo rovný √N. Tedy dvojic je maximálně √N a tím pádem dělitelů maximálně 2√N. Tedy pokud zkoušíme jako K všechny dělitele N, získáme časovou složitost O(N√N) = O(N3/2).
Pořád ale zkoušíme některé dělitele zbytečně. Například pokud existuje šestiúhelník, vždy existuje i trojúhelník (stačí vzít z šestiúhelníku každý druhý vrchol). Takže pokud zkoušíme K = 3, je zbytečné zkoušet i K = 6. Obecně stačí zkoušet jen prvočíselná K. Pokud by existoval mnohoúhelník pro nějaké složené K, bude existovat i pro jeho prvočíselné dělitele – a ty zkoušíme.
Stačí tedy zkoušet prvočíselná K, která dělí N – tedy přesně čísla z prvočíselného rozkladu N. (Rozklad umíme spočítat v čase O(N), takže nás nebrzdí.)
Musíme si dát pozor ještě na jednu věc – hledáme K větší než 2. Nabízí se dvojku v prvočíselném rozkladu prostě ignorovat, ale to nefunguje – nenašli bychom například čtverec. To vyřešíme tak, že pokud je v rozkladu dvojka, vyzkoušíme místo ní K = 4. Rozmyslete si, že jiná sudá K zkoušet nemusíme – buď jsou násobkem čtyř nebo nějakého lichého prvočísla.
Abychom určili časovou složitost při využití pouze prvočísel z rozkladu, musíme odhadnout, kolik jich bude. Protože všechna prvočísla v rozkladu jsou větší nebo rovna 2, platí N ≥ 2r, kde r je počet prvočísel v rozkladu. Odtud dostáváme r ≤ log2 N. Víme tedy, že celý algoritmus má časovou složitost O(N log N).
| log N |
| log log N |
 31-5-3 Kváskový chléb (Zadání)
31-5-3 Kváskový chléb (Zadání)
Máme posloupnost řetězců (popisů kvásků), jejíž první dva prvky jsou Ch1 = Z, Ch2 = P a každý další je zřetězením dvou předchozích: Chi = Chi-2Chi-1. Na vsupu dostaneme n, k, ℓ, chceme vypsat ℓ znaků od k-té pozice z Chn.
Popis struktury kvásku se nápadně podobá Fibonacciho posloupnosti – jen s řetězci místo čísel. Připomeneme, že Fibonacciho posloupnost je definovaná tak, že první dva prvky jsou F0 = 0 a F1 = 1 a každý další vznikne součtem dvou předchozích (Fi = Fi-2 + Fi-1). Začíná takto: 0, 1, 1, 2, 3, 5, 8, 13, ….
Hned vidíme, že délky řetězců Chi jsou Fibonacciho čísla: |Chi| = Fi. Na začátku algoritmu si připravíme pole obsahující Fibonacciho čísla do Fn. To zvládneme jedním cyklem v O(n).
Zadání si trochu zjednodušíme a budeme úlohu řešit pro ℓ= 1 – tedy chceme vypsat jen k-tý znak Chn. Pro více znaků prostě celý postup ℓ-krát zopakujeme.
Struktura Chn vypadá následovně:
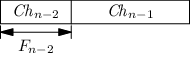
Pro k < Fn-2 je hledaný znak k-tým znakem v levé části (Chn-2), pro k ≥ Fn-2 je hledaný znak (k - Fn-2)-tým znakem v pravé části (Chn-1).
To vede na jednoduché rekurzivní řešení:
- VypišZnak(n, k):
- Pokud k ≥ Fn, skonči s chybou (k mimo rozsah)
- Pokud n = 1, vypiš „Z“ a skonči
- Pokud n = 2, vypiš „P“ a skonči
- Pokud n < Fn-2:
- VypišZnak(n-2, k)
- jinak
- VypišZnak(n-1, k - Fn-2)
Hloubka rekurze je n a v každém kroku uděláme konstantní množství práce (Fn bereme z tabulky přepočítané na začátku). Časová složitost je tedy O(ℓn), paměťová O(n).
Optimalizace pro malá k
Pokud je n hodně velké a k hodně malé, můžeme složitost zlepšit. Všimněme si, že na začátku Chn je Chn-2, na jeho začátku je Chn-4, atd. Třeba pro n=8:
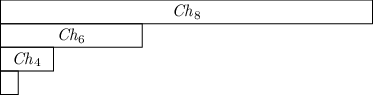
Pokud například k < F4, výsledek pro n=4 bude stejný jako pro n=8. Obecně můžeme n nahradit nejmenším n' se stejnou paritou (to znamená, že pokud bylo n sudé, musí být n' sudé, pro n liché musí být n' liché), pro které platí Fn' ≥ k. Podmínka na paritu je důležitá, protože začátky sudých a lichých kvásků vypadají jinak (např. všechny liché začínají „Z“ a všechny sudé začínají „P“).
To můžeme udělat už během úvodního cyklu, který počítá Fibonacciho čísla. Jakmile během něj narazíme na i se správnou paritou, pro které spočítané Fi je větší než k, cyklus ukončíme a změníme n na i. Zbytek algoritmu pokračuje, jak byl popsán výše.
Co tato změna udělá se složitostí? Všimneme si, že Fibonacciho čísla rostou exponenciálně: Fn = Fn-2 + Fn-1 ≥ 2Fn-2, tedy s každým zvýšením n o dva se Fn alespoň zdvojnásobí.
Nyní si můžeme představit, že například pro liché n začneme s n'=1 a zvyšujeme ho po 2 tak dlouho, dokud nepřesáhneme k. Každým zvýšením se hodnota Fn' alespoň zdvojnásobí, takže celkový počet zvýšení bude maximálně O(log k). Tedy i n' = O(log k). Celková časová složitost bude O(ℓ log k), paměťová O(log k).
 31-5-4 Otesánek ve vývařovně (Zadání) (Komentáře)
31-5-4 Otesánek ve vývařovně (Zadání) (Komentáře)
Než se bezhlavě pustíme do simulace zasedacího pořádku ve vývařovně, tak se nejdříve zamysleme nad jednoduchým pozorováním – do jakého místa se posadí nově příchozí strávník?
Určitě se posadí do nějakého volného místa mezi dva strávníky (případně mezi strávníka a paní u okénka) a v tomto volném místě se určitě posadí doprostřed – protože tím maximalizuje vzdálenost k nejbližšímu ze sousedů. A z těchto volných míst si určitě vybere to nejdelší, protože jakékoliv jiné nemůže vést k větší vzdálenosti od sousedů.
Pro první typ operace (příchod nového strávníka) tak potřebujeme jen datovou strukturu, která nám vždy vrátí nejdelší volné místo ve vývařovně. To z datové struktury odebereme, zapíšeme si pozici uprostřed a pak vložíme do datové struktury dvě menší volná místa vzniklá rozpůlením původního.
Pro druhý typ operace (když strávník dojí a odejde) už budeme potřebovat pár vylepšení navíc. Když strávník odejde, tak potřebujeme spojit dvě volná místa okolo jeho pozice do jednoho nového (většího) volného místa. K tomu se nám budou hodit odkazy z každého strávníka na volná místa okolo něj – pak jen obě volná místa okolo něj odebereme a vložíme do datové struktury jedno větší.
Abychom tyto odkazy zvládli udržovat při příchodech strávníků, kdy se volná místa rozdělují na poloviny, tak ještě budeme potřebovat zpětné odkazy z volných míst na strávníky na okrajích každého volného místa.
Jakou datovou strukturu na tyto operace použít? První volbou, na kterou napovídala i kuchařka, může být nějaký (vyvažovaný) vyhledávací strom, ve kterém pro první operaci v čase O(log N) najdeme největší volné místo (v klasickém BVS to bude prvek nejvíce vpravo), toto místo odebereme a dvě nová vložíme. Pro druhý typ operace naopak dvě místa (na která potřebujeme mít odkazy) odebereme a jedno nové vložíme.
Druhou volbou pak může být lehce upravená halda, která nám umožní mazat i prvky z prostředka haldy. Při prvním typu operace nám stačí odebrat maximum a vložit dva nové prvky. Druhý typ operace po nás ale požaduje odebrání dvou prvků zevnitř haldy, což však můžeme udělat podobně jako při odebírání maxima – prohodíme mazaný prvek na konec, odstraníme ho a nakonec prohozený prvek zabubláme buď nahoru nebo dolů.
Oba postupy zvládnou zpracovat jak příchod tak odchod strávníka v čase O(log N). V obou případech je potřeba nezapomenout na udržování odkazů ze strávníků na volná místa – třeba tak, že strávníky máme v nějakém poli a při každém přesunu volného místa ve vyhledávacím stromě (nebo haldě) aktualizujeme uložené pointery.
Ve vzorovém řešení si ukážeme implementaci s pomocí upravené haldy, jelikož je jednodušší na implementaci než nějaký vyvažovaný vyhledávací strom.
 31-5-5 Přísady na pizze (Zadání) (Komentáře)
31-5-5 Přísady na pizze (Zadání) (Komentáře)
Poslední úloha letošního ročníku KSP byla díky kouzelné krabičce trochu netradiční. Pojďme si proto nejprve připomenout, co s takovou krabičkou můžeme udělat. Na vstup jí můžeme předložit libovolný graf a ona nám řekne, zda nejmenší počet přísad je sudý, nebo lichý. Ale jaké grafy jí máme předkládat? Naše úloha přece dostane na vstupu jen jeden graf. Kde vezmeme nějaký další, abychom krabičku zavolali vícekrát?
Inu nějakým způsobem si graf ze vstupu upravíme. Například můžeme zavolat nejprve krabičku na původní graf. V dalším kroku z grafu jeden vrchol smažeme (včetně všech hran, které do něj vedly) a spustíme krabičku znovu. Co se mohlo stát? Buď se smazáním vrcholu počet potřebných přísad nezměnil, nebo se snížil o jedna.
Všimněte si, že více klesnout nemohl – stačí se na to podívat pozpátku. Pokud existuje pro menší graf správné rozmístění přísad, stačí vrátit vrchol zpět a přiřadit mu zcela novou přísadu. Získali jsme funkční rozmístění, které je jen o jedna větší.
Z toho dostaneme první řešení úlohy. Krabičku postupně voláme na graf a v každém kroku z grafu postupně odebíráme jeden další vrchol. Až dojdeme k prázdnému grafu, víme, že minimální počet přísad pro tento graf je nula. Stačí tedy spočítat, kolikrát se výstup z krabičky změnil, a dostaneme minimální nutný počet přísad.
Pro graf s N vrcholy a M hranami potřebujeme krabičku zavolat N-krát a celková časová a paměťová složitost je O(N+M).
Krabička jako jeden bit
Popsané řešení funguje, ale naším úkolem bylo primárně minimalizovat počet volání kouzelné krabičky. Nedalo by se to zlepšit? Co je principem této úlohy? Z grafu se snažíme „vydolovat“ jedno číslo v rozsahu 0 … N s pomocí krabičky, která nám o grafu umí říct na jedno zavolání jeden bit informace – sudé/liché. Pokud bychom se ptali správně, možná by nám mohlo stačit krabičku zavolat jen log2 N krát.
Takovou složitost má třeba binární vyhledávání. Nešlo by zde nějak použít? Rozhodně ano, pokud bychom měli krabičku, které předáme graf a nějaké číslo L a krabička by nám řekla, zda je nutný počet přísad pro graf větší, nebo menší než dané číslo L. Binárním vyhledáváním hraničního L v rozsahu 0 … N bychom našli správnou odpověď s použitím řádově log2N kroků.
Naší krabičce sice číslo nepředáme přímo, ale můžeme místo toho upravit vstupní graf. Když má graf více komponent, krabička nám vrací informaci o počtu přísad z té komponenty grafu, která jich potřebuje nejvíce. Úprava bude fungovat následovně:
Nejprve zavoláme krabičku na původní nezměněný graf ze vstupu. Zjistíme, zda minimální počet přísad je sudé, nebo liché číslo. Předpokládejme bez újmy na obecnosti, že je tento počet lichý. Do grafu přidáme zcela novou komponentu, jejíž potřebný počet přísad si sami určíme jako nějaké sudé L.
Když se krabičky zeptáme na upravený graf, dostaneme buď nezměněnou odpověď – to v případě, kdy je L menší než nutný počet přísad původního grafu. Nebo se výsledek změní na sudý a my z toho poznáme, že nový graf vyžaduje právě L přísad, a na původní tedy stačí přísad méně než L.
A to je vše. V kombinaci s binárním vyhledáváním dostáváme celé řešení. Zbývá jen uvést, že onou přidávanou komponentou s počtem přísad L je úplný graf s L vrcholy, v literatuře označovaný jako KL. V úplném grafu jsou všechny vrcholy propojeny hranou, takže žádné dva nemohou dostat stejnou přísadu.
Krabičku voláme řádově log2 N krát a časová a paměťová složitost je O(N2), protože nová komponenta má řádově N2 hran. Tuto časovou složitost dosáhneme, pokud budeme v každém kroku vycházet z grafu z předchozího volání. Pokud bychom graf vždy konstruovali znovu, bude časová složitost O(N2 log N).