První série třicátého druhého ročníku KSP
Celý leták v PDF.
První série se ke konci října nachýlila ke svému termínu a proto vám nyní přinášíme naše řešení zadaných úloh. Doporučujeme vám si řešení přečíst, mnohdy se tak můžete přiučit zajímavé nové postupy a triky.
Stejně jako v minulém roce plánujeme po opravení řešení od vás vydat komentáře k úlohám, kde shrneme třeba časté chyby nebo naopak zajímavé alternativní postupy.
Pokud se vám cokoliv nezdá nebo máte nějaký dotaz, neváhejte se ozvat na našem fóru nebo emailem na známou adresu.
Řešení úloh
- 32-1-1: Zkomolené vysílání
- 32-1-2: Stavba rampy
- 32-1-3: Čokoládová tyčka
- 32-1-4: Instalace OS
- 32-1-5: Výhled z vrcholků
- 32-1-6: Data na OSMou
 32-1-1 Zkomolené vysílání (Zadání)
32-1-1 Zkomolené vysílání (Zadání)
| N |
| 2 |
Můžeme si všimnout, že pokud nedošlo ještě k další chybě kromě přidání znaku, najdeme kýženou zprávu neporušenou v prvních nebo posledních D znacích řetězce podle toho, kde přibylo písmeno.
Zvlášť vyzkoušíme, zda tyto dvě možnosti mohly nastat. Nejprve vyzkoušíme možnost s neporušenou původní zprávou na začátku řetězce (v prvních D znacích). Nastavíme index a na 0 a b na D (indexujeme od nuly) a D-krát provedeme následující: ověříme, že jsou znaky na indexu a a b shodné a přičteme k indexům jedničku. Při první neshodě prostě inkrementujeme b a zkusíme to znovu (považujeme b-tý index za index přidaného písmene). Druhá neshoda by už znamenala dvě přidaná písmena a vylučuje tak tuto možnost (tedy že neporušenou zprávu najdeme v prvních D znacích).
Podobně ověříme i druhou možnost, tedy neporušenou zprávu v posledních D znacích. Indexy teď nastavíme na a=D+1, b=0 a postupujeme de facto stejně.
Nyní tedy máme k oběma možnostem informaci, zda mohly nastat. Pokud nemohla nastat ani jedna, musíme vypsat „[chyba]“. Pokud jen jedna z nich, máme vyhráno a nalezli jsme unikátní zprávu. Jakmile mohly nastat obě, musíme ještě ověřit, zda se prvních D znaků shoduje s posledními D. Pokud se shodují, opět máme unikátní zprávu, jinak nevíme, kterou možnost zamýšlela základna poslat a musíme vypsat „[neunikatni]“.
Celý trik spočíval v tom, převést si úlohu na hledání přidaného znaku v řetězci délky D+1. Dvakrát opakujeme iteraci o D krocích, algoritmus tak pro každou zprávu poběží lineárně dlouho vůči její délce.
Na možnou implementaci se můžete podívat v následujícím zdrojáku:
 32-1-2 Stavba rampy (Zadání) (Komentáře)
32-1-2 Stavba rampy (Zadání) (Komentáře)
Prvním důležitým krokem je zjištění, kam vlastně která krabice patří. Proto nejprve setřídíme uspořádané dvojice (výška krabice, počáteční pořadí krabice) podle první složky vzestupně. Z těchto dvojic potom umíme ke každé krabici určit, kolikátá v pořadí bude ve výsledné konstrukci (pro všechny dohromady v lineárním čase).
Následně zjistíme, které krabice bude vlastně třeba prohazovat. Začneme od nějaké krabice K1 a podíváme se, kde má stát na konci prohazování. Pokud nestojí na svém výsledném místě, tak na jejím místě stojí nějaká krabice K2. Pro tuto krabici opět rekurzivně zjistíme, která krabice stojí na jejím výsledném místě, a tak dále, dokud nedojdeme ke krabici Kn, která má stát tam, kde teď stojí K1. Důležité je uvědomit si, že takovou krabici nakonec vždy objevíme.
Posloupnost K1, K2, … , Kn můžeme interpretovat v řeči orientovaných grafů nebo permutací – získali jsme orientovaný cyklus krabic Ki, v němž každá zabírá místo své předcházející. Takových cyklů může být v posloupnosti více. Vhodný způsob, jak detekovat všechny, je projít cyklus, v němž je první krabice, přitom si značit, které krabice v takovém cyklu leží. Poté budeme pokračovat s hledáním cyklu pro další krabici v původním seznamu, která dosud v žádném cyklu neleží. V lineárním čase tedy získáme seznam všech cyklů.
Zaměřme se nyní na to, jak operace prohození dvou krabic cykly mění. Leží-li obě krabice ve stejném cyklu, pak se tento cyklus rozpadne na dva. Leží-li v různých cyklech, tyto dva cykly se spojí. Rampa je postavená, pokud každá krabice stojí na vlastním místě, čili tvoří vlastní cyklus délky 1. Speciálně nejmenší počet prohození pro uspořádání jednoho cyklu je o jednu méně, než je jeho délka.
Tvoří-li všech S>1 krabic s váhami w1, … , wS na začátku jeden cyklus, musíme učinit alespoň S-1 prohození. Každá krabice se přitom triviálně musí alespoň jednou pohnout. Proto minimální cena nutná k setřídění takového cyklu je:
| S |
| i=1 |
(za prohození krabice i platíme wi a váhu nějaké krabice, se kterou ji prohodíme).
Všimneme si, že za tuto cenu dokážeme každý cyklus uspořádat do cílového stavu. Toho dosáhneme posunováním nejlehčí krabice proti směru cyklu, dokud nestojí každá krabice na svém finálním místě.
Zbývá dořešit situaci, kdy máme na počátku více než jeden cyklus, konkrétně za jakých okolností se vyplatí cykly spojovat. Za určitých okolností se totiž vyplatí půjčit si lehoučkou krabici z jiného cyklu a použít ji k posunování v protisměru.
Zaveďme si nezápornou veličinu nazvanou „dotřiďovácí cena“ – d, což bude funkce cyklu (pro cyklus vrátí nějakou hodnotu). Označme w* váhu nejlehčí existující krabice. Pro cyklus C s prvky K1, K2, … , Km a jejich váhami w1, … , wm definujeme d(C) jako:
| m |
| i=1 |
Všimněme si, že d je nulové, právě když je cyklus tvořen právě jednou krabicí. Označme sumu d přes všechny cykly jako D. D je nulové, právě když je seřazování dokončeno. Platí, že součet D s cenou všech již provedených úprav je neklesající. Stačí si rozebrat případy spojování a rozpojování.
Důležité je, že za D je možné za každé situace dostavět rampu pomocí následujícího jednoduchého algoritmu: Pro cyklus z krabic K1 a Km zkontrolujme nerovnost:
Pokud platí, tak vyber nejlehčí krabici a vyměň ji s nejlehčím prvkem. Následně setřiď každý cyklus posunováním nejlehčího prvku proti směru cyklu. Můžeme se snadno přesvědčit, že tyto úpravy postaví rampu za ceny přesně původního D.
Hledání minim cyklů stihneme v lineárním čase vzhledem k počtu krabic. Vypisování správných dvojic prvků, které se mají prohazovat, je již snadné. Celková složitost algoritmu je O(n log n), kde n je počet krabic. Víme rovněž, že rychlejší algoritmus nenalezneme, neboť bychom mohli takový algoritmus používat k třídění posloupností v čase lepším než O(n log n).
 32-1-3 Čokoládová tyčka (Zadání) (Komentáře)
32-1-3 Čokoládová tyčka (Zadání) (Komentáře)
Máme tyčinku s D dílky s různými energetickými hodnotami a chceme zjistit, které dílky má kolonista jíst, aby získal celkem co nejvíce energie, když se v jezení střídá s druhým kolonistou.
Na průběh svačiny se podívejme jako na hru: V každém tahu jeden hráč ukousne jeden z krajních dílků a dostane odpovídající počet bodů. Hráči se po jednotlivých tazích střídají. Cílem každého hráče je samozřejmě získat co nejvíce bodů.
Můžeme si průběh hry odsimulovat – respektive odsimulovat všechny možné průběhy hry a nakonec zjistit, který z nich při optimální hře obou hráčů nastane. V prvním tahu má první kolonista dvě možnosti: může kousat buď zprava, nebo zleva. Stejně tak v každém dalším tahu (až na poslední, kdy zbývá jen jeden dílek) jsou vždy dvě možnosti, které musíme vyzkoušet. Protože dílků je D, musíme vyzkoušet 2D možností a dostaneme algoritmus s exponenciální časovou složitostí.
Ještě zmíním, jak zjistíme, který průběh hry je ten správný, jež hledáme. Nemusí to totiž být ten, při kterém první kolonista získá nejvíc bodů ze všech možných průběhů hry – druhý kolonista totiž také hraje optimálně a nenechá tomu prvnímu nic, co není nutné. Když tedy prohledáváme tyčinku do hloubky a vracíme se z rekurze, tak vždy porovnáme „výhodnost“ kousnutí zleva a zprava pro kolonistu, který je právě na tahu, a ne jen pro prvního.
Exponenciální algoritmus je ovšem příliš pomalý – už pro tyčinku se 40 dílky by běžel déle než čtvrt hodiny a pro 60 dílků bychom se výsledku nedožili. Pojďme si tedy ukázat nějaký polynomiální algoritmus.
Uvažujme všechny možné souvislé úseky tyčinky. Jsou to všechny stavy tyčinky, které v průběhu hry mohou nastat, protože tyčinku ujídáme pokaždé na konci a vždy nám tak zbývá nějaký souvislý úsek původní tyčinky. Máme jeden úsek délky D, což je celá tyčinka. Dva úseky délky D-1, tedy úseky od prvního k předposlednímu dílku a od druhého dílku do konce. Až nakonec D úseků délky 1. Dohromady to je řádově D2/2 úseků. Pro každý úsek nyní zjistíme, kolik bodů může hráč získat, pokud na tomto úseku táhne jako první, a kolik, pokud táhne jako druhý.
Pro úsek délky 1 dostane první hráč počet bodů příslušný danému dílku a druhý hráč nedostane nic. Pro úsek délky k začínající na dílku i a končící na dílku j dostane první hráč větší hodnotu z následujících dvou: buď hodnotu i plus zisk druhého hráče na úseku i+1 až j, nebo hodnotu j plus zisk druhého hráče na úseku i až j-1. Druhý hráč pak dostane zisk prvního hráče na vybraném úseku délky k-1.
Řešením pak bude zisk prvního hráče na úseku délky D. Protože si pro každý úsek můžeme zisk spočítat v konstantním čase z hodnot pro odpovídající kratší úseky, celková časová složitost algoritmu bude O(D2).
 32-1-4 Instalace OS (Zadání)
32-1-4 Instalace OS (Zadání)
Vstup si nahrajeme do paměti jako graf, kde vrcholy představují balíčky a orientovaná hrana z a do b znamená, že balíček b závisí na balíčku a. Nejprve popišme hladové řešení a pak ověřme, zda funguje. Předně nemůžeme vědět, zda se vyplatí začít instalací z prvního, nebo druhého média. To ale nevadí – můžeme totiž zkusit obě možnosti, vybrat z nich tu lepší a časová složitost se asymptoticky nezmění.
Nejprve zkusme začít instalaci z prvního média: Spočítáme si pro každý vrchol, na kolika jiných balíčcích závisí, a speciálně si poznačíme vrcholy, které nezávisí na ničem (neboli vrcholy, do kterých nevede žádná hrana) – ty si přidáme do dvou seznamů podle toho, na kterém z médií se nacházejí. Takové vrcholy určitě existují, jelikož je graf acyklický (jak jsme slíbili v zadání).
Pak začneme se seznamem balíčků bez závislostí z prvního média a pro každý z nich uděláme:
- Vytáhneme vrchol v ze seznamu.
- Označíme v jako nainstalovaný.
- Projdeme všechny vrcholy, do kterých z v vede hrana, a snížíme těmto vrcholům počet závislostí o jedna. Pokud tím některému z vrcholů klesne počet závislostí na nulu, tak ho přidáme na konec správného seznamu (podle toho, na kterém z médií je).
Všimněme si, že pokud nějaký balíček závisel jen na balíčcích ze stejného média nainstalovaných v tomto kroku, tak jsme ho také nainstalovali (tím, že jsme ho přidali na konec seznamu).
Pokud je v tuto chvíli druhý seznam neprázdný, tak zvedneme počítadlo prohození o jedna a uděláme stejný proces s druhým médiem. Pokračujeme do chvíle, než se nám povede označit všechny balíčky za nainstalované (což máme slíbeno, že lze).
Nyní bychom měli mít spočítaný minimální počet prohození, pokud začneme instalaci z prvního média. Algoritmus zopakujeme pro začátek ve druhém médiu a vybereme variantu s nižším počtem prohození.
Proč tento postup funguje? Dokažme si indukcí, že náš postup při určeném počátečním médiu instaluje každý balíček tak rychle, jak to jen lze. Pro balíčky bez závislostí to triviálně platí, ty jsme nainstalovali s nulovým počtem prohození v prvním kroku (případně s jedním prohozením, pokud byly z druhého média). Každý další balíček jsme pak instalovali hned poté, co byly splněny jeho závislosti, a to buď ve stejném kroku (pokud poslední nesplněná závislost byla v rámci stejného média), nebo po jednom prohození (pokud byla z druhého média).
O všech závislostech tohoto balíčku z indukce víme, že byly instalovány tak rychle, jak to jen lze, takže i tento balíček nemohl být při zahájení z daného média instalován rychleji. Počáteční média jsme vyzkoušeli obě dvě, takže náš postup určitě vrací minimální počet prohození, se kterým lze nainstalovat všechny balíčky.
Dvakrát jsme prošli všemi vrcholy grafu, a z každého vrcholu také všemi jeho hranami, asymptoticky tak algoritmus běží v čase O(N+M) (kde N značí počet vrcholů a M počet hran).
 32-1-5 Výhled z vrcholků (Zadání)
32-1-5 Výhled z vrcholků (Zadání)
V úloze chceme najít takovou cestu na vyšší vrchol, jejíž nejnižší bod je co nejvýše, a sekundárně chceme, aby byl cíl cesty také co nejvýše. Pro začátek předpokládejme, že nejnižším bodem je ten počáteční. Z počátečního políčka spustíme prohledávání do šířky, které hledá nejvyšší takto dosažitelný vrcholek, ale má nastavenou laťku: má zakázáno šířit se do políček, která leží níže, než počáteční.
Jakmile naše prohledávání do šířky doběhne, podíváme se na nejvyšší nalezený vrcholek. Pokud se nachází výše než počáteční, tak můžeme skončit a vypsat cestu na tento vrcholek, protože i kdyby existovaly vyšší vrcholky, cesta na ně jistě povede přes nějaký bod, který se nachází níže, než počáteční.
Pokud ale žádný vyšší nenajdeme, tak musíme zkusit hledat i takové vrcholky, do kterých vede cesta přes nižší bod, než je počátek. Snížíme tedy laťku na úroveň nejvyššího nižšího políčka, než dosavadní laťka, a spustíme prohledávání znovu. Toto opakujeme, dokud není nejvyšší navštívený vrcholek po skončení prohledávání vyšší, než počáteční.
Tento postup jistě najde správný cíl cesty, ale je pomalý: v nejhorším případě bude nutné laťku snížit tolikrát, kolik je různých hodnot výšky políček na mapě, tedy O(K)-krát, kde K je počet různých výšek. Časová složitost by tedy byla O(NK), což v nejhorším případě, kdy K=N, dá složitost až O(N2).
Zrychlujeme
Když se nad tímto řešením zamyslíme, zjistíme, že pomalá část je především to, že při každém spuštění BFS procházíme znovu i políčka, která jsme prozkoumali už v předchozích iteracích. Samozřejmě přes ně může vést cesta ke hledanému vrcholku, ale rozhodně se v nich nenachází.
Při každém spuštění BFS si proto zapamatujeme políčka, která jsou příliš nízká a neprošla laťkou. Každé nové BFS nebudeme spouštět znovu ze startu, ale právě ze všech takto nalezených políček, která mají právě výšku nové laťky, a při průchodu se nebudeme vracet na místa, která byla prozkoumána předchozími iteracemi. Tím pádem každé políčko navštívíme ve všech iteracích BFS dohromady nejvýše jednou.
Ještě potřebujeme efektivně najít po dokončení nějakého BFS novou laťku a všechna příslušná počáteční políčka. K tomu nám poslouží maximová halda, do které si budeme ukládat seznamy nalezených polí, které mají danou výšku, tato halda bude řazena právě podle výšek polí. Odkazy na jednotlivé seznamy budeme mít také ve slovníku (hešovací tabulce), kterou budeme také indexovat výškami políček. To nám umožní efektivně přidávat nová políčka, která leží pod současnou laťkou.
Cestu z počátečního pole do cílového nalezneme tak, že při BFS si při každém objevení nového políčka zapamatujeme, odkud jsme na něj poprvé narazili. Pak můžeme cestu zrekonstruovat postupně směrem od cíle ke startu.
Časová složitost rychlého řešení bude O(N+K log K), kde K je počet unikátních výšek vrcholů. Samotné BFS projde každé políčko nejvýše jednou a podílí se tak na časové složitosti pouze časem O(N), ale pro každou novou výšku budeme muset do haldy v čase O(log K) přidat nový seznam (a možná ho v budoucnu i odebrat) což zabere celkem O(K log K). V nejhorším případě, když K=N, bude časová složitost až O(N log N).
 32-1-6 Data na OSMou (Zadání) (Komentáře)
32-1-6 Data na OSMou (Zadání) (Komentáře)
Protože je seriál hlavně praktický, primárně vás asi budou zajímat (okomentované)
zdrojové kódy. Stejně jako v zadání nabízíme jazyky Go, C# a Python 3. Tady
v textu nabízíme jen stručný princip řešení a pár užitečných rad a triků do
dalších dílů. Jestli vám něco nebude jasné, tak se určitě ptejte, rádi odpovíme
a případně něco doplníme.
Úkol 1 – Hledání unikátních ulic [3b]
Tato úloha byla hlavně o vyzkoušení si načítání vstupního XML, se samotným zpracováním názvů ulic už jste asi moc problémů neměli.
Načtení OSM XML je snad dostatečně detailně popsáno na webu v technické příručce k seriálu. Mimo to si stačilo vyrobit hashovací tabulku (pole indexované názvy ulic), případně přímo využít podporu pro množiny ve vašem oblíbeném jazyce (většinou se dá najít pod názvem hashset) a do ní všechny ulice postupně přidávat. Do paměti by se měly vejít i všechny názvy z celé Evropy, takže nebylo potřeba vymýšlet nic moc sofistikovaného.
 Co kdyby se ulice do paměti nevešly? Lze to samozřejmě vyřešit návštěvou nějakého
obchodu s elektronikou nebo zapůjčením serveru v cloudu, ale to je takové málo
programovací řešení. Když se zamyslíme, jak problém obejít softwarově, tak to
třeba půjde aplikovat i pro náročnější problémy, kde by hardwarové řešení bylo
už moc drahé. V první fázi bychom si mohli vypisovat všechny nalezené názvy ulic
do nějakého souboru na disku. Poté bychom si mohli tento soubor opět projít
a roztřídit si ho třeba podle počátečního písmena do menších souborů, což bychom
mohli opakovat tak dlouho, dokud by se nám každý ze souborů nevešel do paměti.
Pak už si zvládneme každý soubor samostatně zpracovat v paměti (nechat z něj jen
unikátní názvy a spočítat jejich počet) a získat celkový výsledek.
Co kdyby se ulice do paměti nevešly? Lze to samozřejmě vyřešit návštěvou nějakého
obchodu s elektronikou nebo zapůjčením serveru v cloudu, ale to je takové málo
programovací řešení. Když se zamyslíme, jak problém obejít softwarově, tak to
třeba půjde aplikovat i pro náročnější problémy, kde by hardwarové řešení bylo
už moc drahé. V první fázi bychom si mohli vypisovat všechny nalezené názvy ulic
do nějakého souboru na disku. Poté bychom si mohli tento soubor opět projít
a roztřídit si ho třeba podle počátečního písmena do menších souborů, což bychom
mohli opakovat tak dlouho, dokud by se nám každý ze souborů nevešel do paměti.
Pak už si zvládneme každý soubor samostatně zpracovat v paměti (nechat z něj jen
unikátní názvy a spočítat jejich počet) a získat celkový výsledek.
Výsledky: Na malém datasetu (Brno) našla naše řešení celkem 1924 unikátních názvů ulic, na velkém datasetu (Evropa) to bylo 3 358 369 názvů a našemu Go řešení to zabralo 2 hodiny a 53 minut (Pouštěli jsme řešení jednovláknově na notebooku s i7-8550U na frekvenci 4 GHz a s 32 GB RAM). Navíc jsme si i spočítali statistiku názvů, takže pokud se na ně chcete podívat, soubory jsou zde:
Ulice v Brně: ulice_brno.txt [25.9KB]
Ulice v Evropě: ulice_europe.zip [18.2MB]
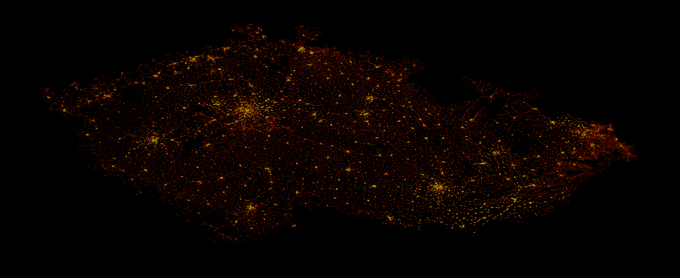
Úkol 2 – Vykreslení heat mapy [5b]
Cílem úlohy bylo spočítat, kolik budov se nachází v jednotlivých pixelech
výsledného obrázku. Na to potřebujeme nejdříve zjistit, kde se vlastně domy
nachází, což není úplně zdarma. Budovy jsou cesty (tag way), takže
neobsahují žádné informace o poloze, jen odkazy na vrcholy pomocí tagu nd.
Budeme tedy muset projít všechny cesty s tagem building a nahrát si do
nějaké hashovací tabulky ID prvních odkazů na vrcholy. Pak budeme muset projít
celý soubor znovu, abychom si načetli polohy vrcholů, které máme zaznamenat do
obrázku. Kdybychom to udělali naopak a nahráli si nejdříve všechny vrcholy do
paměti, tak bychom potřebovali o hodně víc paměti – budov je řádově méně než
všech vrcholů. Takto nám stačí si pamatovat jen 8 bajtů (64 bitový identifikátor
vrcholu) pro každý dům, kterých je v Evropě cca 170 milionů – to je asi
1.3 GB, takže i s režijí hashovací tabulky se bezpečně vejdeme do
2 GB paměti.
Další nástrahou, kterou je potřeba překonat, je stanovení přepočtu jednoho pixelu výsledné heatmapy na zeměpisné souřadnice. Na to si budeme muset na mapě vymezit obdélník podle nejextrémnějších bodů (minimální a maximální souřadnice) – takové body si můžeme lehce najít během prvního průchodu. Poté už snadno spočítáme přepočet jednoho pixelu heatmapy na souřadnice a umíme tak pro každý bod rozhodnout, do jakého políčka patří: od bodu odečteme dolní levý roh vymezujícího obdélníku a výsledek vydělíme po složkách šířkou a výškou obdélníku. Tím dostaneme souřadnice v jednotkovém čtverci (v rozsahu 0 až 1), které pak zase vynásobením velikostí výsledného obrázku převedeme na pozici pixelu.
Potom, co budeme mít poznamenané ID vrcholů k zakreslení do heatmapy, znovu projdeme všechny vrcholy. Když potkáme nějaký, jehož ID máme uložené v hashovací tabulce, tak zvedneme počítadlo pro daný pixel heatmapy o jedna. Až spočítáme, kolik do každého pixelu spadá budov, tak zbývá jen převést tuto informaci na barvu. Můžeme samozřejmě jednoduše nastavit všem RGB složkám stejné číslo, z čehož dostaneme jednoduchou šedou mapku. Reálně ale bude lépe vypadat, když použijeme více barev, například podobně jako se v mapách počasí zobrazují srážky. Možností je tady opravdu mnoho a netroufneme si tvrdit, která je „ta správná“.
Poznámka: Ještě si musíme uvědomit, že když si body poznamenáváme do hashovací tabulky (abychom při druhém průchodu uměli pro každý bod v XMLku rychle najít, zdali ho máme započítat do heatmapy), tak tím přijdeme o duplicitní záznamy – je možné, že dva různé domy budou mít stejný první bod, ale my ho chybně započítáme jen jednou. Není nám ale známo, že by to byl nějak zvlášť častý jev a při kreslení obrázku si můžeme dovolit trochu nepřesností.
Výsledky: Zde se můžete podívat na výsledné heatmapy spočítané pro Brno, ČR a Evropu. Od černé přes červenou až po žlutozelenou roste hustota budov (a všimněte si také deformace způsobené tím, když bereme zeměpisnou šířku jako souřadnicové osy bez jakéhokoliv přepočtu).
Spočítání heatmapy pro Evropu zabralo našemu Go řešení na výše zmíněném hardware 4 hodiny 46 minut.
Úkol 3 – Pítka v Brně a v Alpách [8b]
Jádrem úlohy je naučit se filtrovat podle polygonu. Prvním krokem bude jeho načtení do paměti. Na to je potřeba si najít relaci, podle ní si najít cesty a k cestám si najít body. Cesty si pak rozdělíme na úsečky a ty si uložíme do paměti. Tím se dostaneme na tři průchody celým souborem jenom kvůli načtení polygonu a tak nemusí být špatný nápad si ho uložit na disk a pak načítat jenom ten – může nám to docela urychlit debugování problémů v dalších fázích výpočtu.
Dále budeme potřebovat umět rozhodnout, jestli je daný bod uvnitř nebo vně polygonu. To je starý známý problém, na který jsme odkazovali už ze zadání, a tady se s ním setkáváme v jeho obecné variantě – oba zadané polygony jsou nekonvexní a tak nejde uplatnit některé z primitivnějších postupů.
Jedním z možných řešení pro nekonvexní polygony je natáhnout si z daného bodu polopřímku libovolným směrem a spočítat, kolikrát protla stranu mnohoúhelníka. Nebudeme si komplikovat život a natáhneme polopřímku doprava po ose X, protože je pak docela jednoduché zkontrolovat, jestli se s ní nějaká úsečka protíná. Jak budeme třeba takovou úsečku ab vůči bodu P kontrolovat?
- Předpokládejme, že ay ≤ by (jinak body prohodíme).
- Úsečka musí mít konce na opačných stranách naší polopřímky – to zjistíme prostým porovnáním Py s kraji úsečky. Musí platit ay ≤ Py ∧ Py < by.
- Vezmeme si vektor ab→ a spočítáme si, kde budeme nabývat stejného y
jako bod P:
t =
ay - Py ay - by - Spočítáme x v bodě protnutí:
ax + t·(bx-ax)
- Nakonec jenom porovnáme, že spočítaný bod leží napravo od P (že patří do polopřímky vycházející z P).
Pak už stačí projít všechny body které mají správné tagy, porovnat je s polygonem a vypsat. Abychom porovnávání ještě o něco urychlili, tak se ještě hodí předřadit kontrolu na to, jestli zkoumaný bod leží v obdélníku vymezeném nejextrémnějšími body polygonu a pak teprve spustit výše popsanou kontrolu.
Výsledky: Celkově tak umíme výše popsaným způsobem vyřešit úlohu na čtyři průchody. Nároky na paměť jsou maličké, protože polygon obsahuje docela málo bodů. V Brně jsme nalezli celkem 15 pítek, v Alpách 25003 a našemu Go řešení to na výše zmíněném hardware trvalo 9 hodin a 13 minut.
Pítka v Brně: pitka_brno.txt [163B]
Pítka v Alpách: pitka_alpy.txt [265.3KB]
Poznámka na konec: Druhá, poněkud méně programovací možnost by byla použít nějaký z nástrojů na výřezy z OSM map, například osmconvert. Jeho přesné použití lze nalézt na OSM wiki. Naším cílem bylo spíše si ukázat, jak se dají takové věci naprogramovat, než si procvičit stahování nástrojů z internetu. Ale jestli vás zajímá, kde se dají sehnat výřezy Hrochova Týnce, tak tady je odpověď.
Obecné triky – Paralelizace parsování
 Nejpomalejší část programu byl pravděpodobně XML parser, mohli bychom proto
zkusit načítat XML paralelně na více jádrech procesoru najednou. Dnes už
i nejlevnější počítače mají alespoň dvě jádra a může tak běžet více programů
najednou. Můžeme tedy v našem programu využít více vláken, která pak poběží na
různých jádrech procesoru najednou. Vícevláknové programování není úplně
jednoduché téma a dal by se o něm napsat celý seriál, takže popíšeme zpracování
ve více vláknech jen velmi stručně.
Nejpomalejší část programu byl pravděpodobně XML parser, mohli bychom proto
zkusit načítat XML paralelně na více jádrech procesoru najednou. Dnes už
i nejlevnější počítače mají alespoň dvě jádra a může tak běžet více programů
najednou. Můžeme tedy v našem programu využít více vláken, která pak poběží na
různých jádrech procesoru najednou. Vícevláknové programování není úplně
jednoduché téma a dal by se o něm napsat celý seriál, takže popíšeme zpracování
ve více vláknech jen velmi stručně.
Protože parsování XML závisí na výsledku předchozích operací, tak není vůbec snadné vymyslet, jak parser rozdělit do více vláken. Navíc bychom museli přepsat parsovací knihovnu, která už je i jednovláknová asi dost složitá, takže tudy cesta nevede. Můžeme ale XML soubor rozdělit na několik menších a ty pak načítat najednou různými parsery. Bude potřeba jenom slévat jejich výstup – stream načtených elementů – a to už není moc složité.
Rozdělení souboru můžeme udělat třeba tak, že ho načteme normálním XML parserem, ale namísto zpracování budeme elementy rozdělovat rovným dílem třeba do čtyř různých souborů. Toto zpracování bude sice trvat déle, ale rozdělený soubor pak můžeme po tomto předzpracování již načítat paralelně.
Je i několik dalších možností, jak si soubory inteligentně rozdělit, abychom ušetřili nějaký čas. Například je docela dobré si dát zvlášť vrcholy, cesty a relace, protože když jsme chtěli načíst jednu relaci, museli jsme třikrát projít všechny vrcholy, což trvá zbytečně dlouho.