Třetí série třicátého druhého ročníku KSP
Celý leták v PDF.
Letošní vánoční číslo KSP, které je zároveň třetím číslem jubilejního 25-tého
ročníku KSPčka, vám právě přistálo ve vaší schránce nebo na vašem monitoru.
Opět jsme si pro vás připravili 5 vypečených úloh (z toho nějaké
praktické) a k nim navíc pokračování datového seriálu. Seriál po dvou minulých
dílech opouští OSM a bude si hrát s úplně novými daty – jízdními řády. Proto
se nebojte do seriálu zapojit, i pokud vám OSM data nesedla. A závěrem tohoto
čísla je kuchařka o tocích v sítích.
Připomínáme, že se z každé série stále započítává 5 nejlépe
vyřešených úloh (tedy nemusíte vyřešit úplně všechny a i tak můžete dosáhnout
na plný počet bodů). Také se vám body za úlohy přepočítávají podle vašeho
služebního stáří – na přesnou definici se podívejte do pravidel na webu.
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek.
Úspěšným řešitelem se stává ten, kdo získá za celý ročník (této kategorie) alespoň
50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice
pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít
letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě.
Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů,
darujeme KSP propisku, blok, placku a možná i další překvapení.
- Odměna série: Každému, kdo získá více než 3 body ze seriálu, pošleme sladkou odměnu.
Zadání úloh
Na konci minulého dílu jsme opustili Hefaistos s kolonisty na palubě uprostřed
základny zasažené iontovou bouří. Postupně se začaly hroutit štítové emitory
a bylo to na vašem hlasování, o co by se posádka měla pokusit. Vybrali jste
volbu, že se mají pokusit vzlétnout a dosáhnout orbity.
* * *
„Všichni připoutat, nouzový start!“ křikla kapitánka přes vnitřní interkom.
„Na můj povel odpojte externí štítové emitory. Hned potom chci maximální
výkon do motorů. Tři… dva… jedna… teď!“
Následující sekundu se stala spousta věcí. Nejprve štítový generátor Hefaista
dramaticky snížil svůj výkon, aby se vzápětí od trupu oddělily svorky s kabely
doposud vedoucími k štítovým emitorům na okraji kolonie. Hned jak zmizela
bariéra bránící iontové bouři v postupu, tak se vysokoenergetické částice
vrhly do kolonie – blesky začaly tančit po vnějších budovách kolonie a trhat je
na kusy. Současně s tím ale pilot Hefaista spustil program nouzového vzestupu
na orbitu a atmosférické motory se opřely do okolní země. Devítisettunová loď
se začala rychle zvedat.
Nebylo to však dostatečně rychle – přes proud výfukových plynů pronikl jeden
z blesků iontové bouře do atmosférického motoru na pravoboku. Motor samotný to
sice přežil, ale část řídících obvodů se spálila na škvarek a výboj pronikl i dál
do řídící elektroniky a způsobil množství zkratů. Hlavní řídící počítač Hefaista
se odmlčel, ale naštěstí měly jednotlivé motory již zadané profily letu a během
následujících bouřlivých minut dostaly loď až na oběžnou dráhu.
Potom, co všichni přestali být tlačeni do svých sedaček a naopak se po
potemnělém interiéru ochromené lodě začaly vznášet neupevněné předměty, vrhla se
posádka hned do zkoumání škod. Prvním krokem bylo izolování vyzkratovaných
systémů, aby opět mohli nahodit hlavní počítač.
 32-3-1 Zkrat (12 bodů)
32-3-1 Zkrat (12 bodů)
 Systémy hvězdné lodě Hefaistos jsou ochromené, protože část obvodů byla vyzkratována.
Hlavní inženýr potřebuje nahodit počítačové jádro, ale to nelze,
dokud existuje spojení počítačového jádra a místa zkratu.
Systémy hvězdné lodě Hefaistos jsou ochromené, protože část obvodů byla vyzkratována.
Hlavní inženýr potřebuje nahodit počítačové jádro, ale to nelze,
dokud existuje spojení počítačového jádra a místa zkratu.
Energetickou síť si můžeme představit jako energetické uzly spojené vodiči (jeden
vodič spojuje vždy dva energetické uzly), kde v jednom energetickém uzlu je zkrat
a do jiného energetického uzlu je zapojené přímo počítačové jádro.
Hlavní inženýr bude muset přerušit několik vodičů tak, aby neexistovala žádná
cesta mezi místem zkratu a počítačovým jádrem. Vodiče jsou ale špatně dostupné,
takže by jich chtěl hlavní inženýr přerušit co možná nejméně. Naprogramujte
algoritmus, který mu určí, jaké vodiče má přerušit.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete mezerou oddělená čtyři čísla N,
M, z a p udávající počet energetických uzlů, počet vodičů mezi nimi, index
energetického uzlu se zkratem a index energetického uzlu s počítačovým jádrem
(energetické uzly indexujeme od nuly). Na dalších M řádcích je pak vždy
dvojice mezerou oddělených čísel a a b udávající, že mezi energetickými uzly
a a b vede vodič.
Formát výstupu: Na první řádek výstupu vypište číslo K udávající kolik
nejméně musíme přerušit vodičů, abychom oddělili zkrat a počítačové jádro.
Na dalších K řádcích pak vypište indexy vodičů, které musíme přerušit (index
vodiče je jeho pořadí na vstupu, indexujeme opět od nuly, na pořadí indexů
na výstupu nezáleží). Pokud existuje více stejně dobrých řešení, můžete vypsat
libovolné z nich.
Ukázkový vstup:
9 13 7 2
0 2
4 0
2 3
1 2
1 3
0 1
2 4
3 5
4 6
6 7
6 8
7 5
7 8

V příkladu výše stačí k oddělení dvou zvýrazněných vrcholů (zkratu a hlavního
počítače) přerušit dva vodiče mezi uzly 4-6 a 3-5. Stejně tak by fungovalo
i přerušení vodičů 4-6 a 5-7.
Řešení
Po zprovoznění hlavního počítače a obnovení části systémů (ke spokojenosti
žaludku kolonistů i pole umělé gravitace) se na můstku sešla část posádky na
poradě.
„Jsme bez hyperprostorového pohonu, řídící obvody jsou na škvarek a nevím,
jestli to půjde opravit,“ oznámil všem hlavní inženýr.
„Nepřišlo vám na té iontové bouři něco divného? A na té základně v horách?“
načal diskuzi mariňák Drake. „Skoro jako by tady někdo vyvíjel tajnou zbraň,“
zapřemýšlel nahlas.
„A když se jim něco nepovedlo a přiletěli jsme my, tak se pokusili zamést
stopy…“ rozvinula jeho teorii kapitánka. Pak se otočila na komunikačního
důstojníka: „Můžeme navázat spojení s velením na Antaraxu?“
Zax zavrtěl hlavou. „Ne, je tu rušení od iontové bouře na planetě, ale díky
němu asi nejsme vidět ani my, dokud nezapneme motory. A navíc jsem si všimnul,
že někdo mezitím překonfiguroval družice vypuštěné kolonií – změnily
své komunikační linky a vytvořily novou síť, do které nejsme zapojení.“
„Můžeme je nějak napíchnout?“ zapřemýšlela kapitánka. „No když se nám
povede odhalit jejich propojení, tak možná ano…“ řekl Zax a pustil se do
práce.
 32-3-2 Hledání konstelace (12 bodů)
32-3-2 Hledání konstelace (12 bodů)
Komunikační důstojník Zax by potřeboval odhalit v jaké konstelaci jsou družice
na oběžné dráze. Každou družici si můžeme představit jako vrchol a přímé
propojení mezi dvojicí družic jako hranu nějakého grafu.
Graf neznáme, ale povedlo se nám zachytit nějaké servisní zprávy – některá by
mohla udávat tvar této konstelace.
Přesněji se nám povedlo zachytit posloupnost N čísel, o které si myslíme, že
to jsou počty propojů, které každá družice má (v grafové terminologii bychom
toto číslo nazvali stupněm vrcholu). Nejsme si ale jistí, jestli zachycená
posloupnost popisuje nějakou konstelaci – vymyslete proto algoritmus, který pro
zadanou posloupnost N čísel (uspořádaných od nejmenšího po největší) rozhodne,
jestli tato posloupnost může popisovat nějaký graf.
Můžete k tomu použít znalost věty o skóre.
Tato věta říká, že posloupnost N čísel d1, d2, … popisuje graf
s vrcholy o stupních d1, d2, … právě tehdy když upravená posloupnost, ze které
odebereme největší stupeň dN a odečteme od dN zbylých největších stupňů
jedničku, také popisuje graf. Jednoduchá představa je, že z původního grafu
odebereme vrchol s největším stupněm, který byl spojen s dalšími dN vrcholy
s největším stupněm.
K vyřešení úlohy nepotřebujete znalost důkazu této věty – můžete nám věřit, že
platí. Pouhé naivní použití věty v algoritmu ale na moc bodů stačit nebude – chceme od vás
algoritmus, který zvládne o zadané posloupnosti rozhodnout, jestli tvoří skóre
nějakého grafu, v co nejlepším čase. Plného počtu bodů půjde dosáhnout jen za
řešení v lineárním čase vzhledem k velikosti daného grafu, neboli v O(N+M).
Řešení
Zatímco se Zax pokoušel nabourat se do družicové konstelace, tak kapitánka
debatovala s ředitelem kolonie. Materiál pro stavbu tajné základny (nemluvě
o spoustě jiné techniky) musel být na planetu nějak dopraven, a to pravděpodobně
na palubě běžných zásobovacích lodí.
Při kopírování hlavního počítače kolonie získali i soubory o různých kontejnerech
dopravených na planetu a naopak v tajné základně získali inventární seznam
jejich skladu – teď to jenom napasovat na sebe a možná to dá nějaké zajímavé
indicie. Kapitánka s ředitelem se dali do identifikace kontejnerů, do kterých
by se různé věci nalezené na tajné základně vešly.
 32-3-3 Kontejnerové počty (11 bodů)
32-3-3 Kontejnerové počty (11 bodů)
Kapitánka se ředitelem kolonie by chtěli rychle vyfiltrovat kontejnery, do
kterých se vejde předem daná hromada vybavení. Kontejnery jsou kvádry o rozměrech
A×B×C s maximální délkou strany K.
Protože hromada vybavení nemá žádný hezký pravidelný tvar (různé tyče, zahnuté
potrubí, kulaté nádrže, …), tak se nedá lehce určit, jak velký kontejner je
potřeba. Kapitánka s ředitelem si vždycky vezmou pevnou hromadu vybavení a pak
zkoumají, do jakého kontejneru by se vešla. Pro zadané A, B a C umí určit
(poměrně náročným a zdlouhavým postupem), jestli se vybavení do takového
kontejneru vejde, nebo ne.
Protože je ale možných velikostí kontejnerů řádově K3, tak se jim nechce pro
každou kombinaci rozměrů samostatně počítat, jestli se věci vejdou – ocenili by
drobnou pomoc.
Ohledně kontejnerů platí jediné pravidlo, a to, že pokud se zadaná hromada
vybavení vejde do kontejneru A×B×C a tento kontejner se (nějak
pravoúhle otočený, šikmé umístění neuznáváme) vejde do druhého kontejneru
A'×B'×C' (tedy že otočený první kontejner není v žádné ose větší
než druhý kontejner), tak se vybavení vejde i do druhého kontejneru.
Například můžeme říci, že pokud se vybavení vejde do kontejneru
5×2×10, tak se určitě vejde i do kontejneru 2×10×11.
Naopak o kontejneru 9×9×9 ale nemůžeme prohlásit nic (a budeme se
muset zeptat lidské obsluhy).
Vaším úkolem je vymyslet algoritmus, který (pro pevně danou hromadu věcí)
nejdříve položí dotazy na nějaké velikosti kontejnerů kapitánce se ředitelem,
a pak bude umět správně odpovědět na jakýkoliv dotaz pro A,B,C ≤ K. Vaším
cílem je minimalizovat počet „pomalých“ dotazů na kapitánku se ředitelem –
minimalizujte i multiplikativní konstantu a zkuste dokázat, že na méně dotazů už
to nelze.
 Lehčí varianta (za 7 bodů): Vyřešte úlohu jenom ve 2D, tedy namísto kvádrů uvažujte pouze
obdélníky o rozměru A×B.
Lehčí varianta (za 7 bodů): Vyřešte úlohu jenom ve 2D, tedy namísto kvádrů uvažujte pouze
obdélníky o rozměru A×B.
Řešení
Po odečtení kontejnerů, které s jistotou byly rozebrané v kolonii, a kontejnerů,
které podle výpočtu byly použity pro materiál na tajné základně, dospěli k tomu,
že schází zhruba půl tuctu kontejnerů, které musely být dovezené ještě někam
jinam. Materiál v nich by stačil na stavbu zhruba poloviční základny, než byla
ona objevená tajná základna v horách. Teď už ji jen najít…
Zaxovi se mezitím povedlo zjistit konfiguraci družicové sítě. Jenom s pomocí
manévrovacích trysek se Hefaistos pomalu přesunul k jedné z družic. Když pilot
stabilizoval loď dvacet metrů od družice, tak se k ní vydali dva členové posádky
ve skafandrech a v domluvenou chvíli jí přerušili napájení. Přesně v tu samou
chvíli anténní soustava Hefaista ožila a začala se vydávat za právě odpojenou
družici – snad si nikdo ničeho nevšimne.
Poté dopravili družici skrz malý hangár pro servisní raketoplán do nákladního
prostoru Hefaista, kde se na ni vrhl hlavní inženýr. Uvnitř těla družice
narazil na zajímavou komponentu, která vypadala dost jako prototyp – spousta
drátů zapojených do různých konektorů na různých přístrojích. Po chvíli rozebírání
si ale s hrůzou uvědomil, že si nedělal poznámky, kam který drát patří…
 32-3-4 Zmatek v konektorech (11 bodů)
32-3-4 Zmatek v konektorech (11 bodů)
Hlavní inženýr rozebral zkoumanou družici, ale teď by potřeboval pozapojovat
vytažené dráty nazpět. Má teď v ruce spoustu koncovek, ale neví, do kterého
konektoru kterou koncovku zapojit. Naštěstí mají koncovky i konektory více
různých tvarů, ale nejsou bohužel úplně unikátní. Přesněji každou koncovku lze
zapojit do právě dvou různých konektorů.
Vymyslete algoritmus, který pro zadané koncovky (pro každou koncovku dostaneme
zadaná čísla právě dvou konektorů, kam pasuje) najde správné zapojení, nebo
oznámí, že to nelze. Správné zapojení je takové, kdy je každá koncovka zapojená
do právě jednoho konektoru a v žádném konektoru není více než jedna koncovka.
Příklady:
- Koncovky (1,2) a (3,4) lze triviálně zapojit třeba tak, že první koncovku
zapojíme do konektoru 1 a druhou do konektoru 4.
- Koncovky (1,2), (2,3) a (3,1) lze také správně zapojit.
- Naopak koncovky (1,2), (1,3), (1,4), (3,2), (3,4) a (5,6) správně
zapojit nelze.
Řešení
„Někdo ty satelity upravil kapitáne. Tohle jsem ještě neviděl, ale podle
zapojení a komponent bych hádal, že to nějakým způsobem ovládá směrování
iontové bouře. Má to celkem velkou energetickou náročnost, ale za chodu to už
čerpá energii z iontové bouře. Na detaily se mě neptejte, sám tomu úplně nerozumím,“
vysvětloval po pár hodinách zkoumání satelitu hlavní inženýr McCormack ostatním.
„Co je ale zajímavé, je, že ve stand-by režimu to musí být extrémně úsporné,
aby to zvládlo parazitovat na normálních součástkách satelitu. A to si to
každou hodinu posílá docela komplikované zprávy po celé síti…“
 32-3-5 Energetická náročnost (10 bodů)
32-3-5 Energetická náročnost (10 bodů)
Pro propočty ohledně fungování satelitní sítě je potřeba spočítat její
energetickou náročnost ve stand-by režimu. Již jsme zjistili, že satelity jsou
pospojované do souvislé sítě ve tvaru stromu a známe energetickou náročnost
poslání zprávy mezi propojenými satelity (jinými slovy máme strom s ohodnocenými
hranami).
Každou hodinu každý z N satelitů vyšle zprávy všem N-1 zbylým satelitům.
Zprávy putují po satelitní síti nejkratší cestou a energie spotřebovaná na
předání jedné zprávy po nějaké „hraně“ odpovídá ohodnocení této hrany.
Protože komunikační protokol navazuje nové spojení pro každou zprávu, tak
předání k zpráv po hraně ohodnocené „cenou“ c stojí celkově k·c
jednotek energie.
Nás by zajímala celková spotřebovaná energie když každý ze satelitů vyšle zprávu
každému jinému. Vymyslete algoritmus, který to pro zadanou síť zvládne spočítat
co nejrychleji.
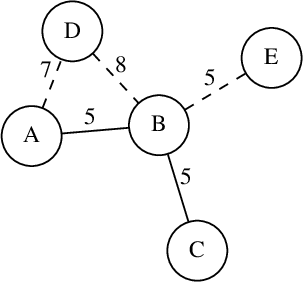
Příklad: Pro satelitní síť na obrázku níže je celková spotřebovaná energie
pro vyslání všech zpráv ze všech 5 satelitů celkem 152 jednotek energie.
Zprávy ze satelitu A spotřebují 27 jednotek energie, ze satelitu B také
27 jednotek, ze satelitu C 24 jednotek, ze satelitu D 34 jednotek a ze
satelitu E 40 jednotek energie.
Řešení
Díky všem indiciím se povedlo posádce Hefaista koncem dne lokalizovat druhou
tajnou základnu na planetě. Pokud mohli hádat, tak právě odsud byly kontrolovány
iontové bouře a tam sídlil někdo, kdo se rozhodl, že nepotřebuje svědky, kteří
vědí příliš mnoho.
Nadsvětelná komunikace s velením na Antaraxu byla pořád blokovaná a následky
iontové bouře, které oslepovaly senzory tajemné základny a ukrývaly poničeného
Hefaista, postupně slábly. Brzy je odhalí a těžko říci, jaké další akce
podniknou k tomu, aby se zbavili svědků. Nyní byla ale karta stále na straně
Hefaista, jenom se rozhodnout, co podniknout…
* * *
Opět rozhodněte o tom, jak má příběh pokračovat. Hlasujte do 10. února
v anketě.
Třetí díl příběhu pro vás sepsal
Jirka Setnička
 32-3-6 Jízdní řády (15 bodů)
32-3-6 Jízdní řády (15 bodů)
V tomto dílu se od map přesuneme k dalšímu druhu reálných dat, se kterým se
většina z vás v každodenním životě potkává celkem často: jízdním řádům veřejné
dopravy. Upozorňujeme, že v tomto dílu seriálu budete používat jiné datové
sady než v předchozích dvou, podrobněji o nich níže.
Kde vzít data
Dlouho bylo v ČR velmi obtížné až nemožné sehnat data jízdních řádů ve strojově
zpracovatelném formátu. V posledních letech se díky úsilí mnoha organizací
i jednotlivců situace zlepšuje.
Praha. Nejjednodušší je situace v Praze a okolí, kde jsou k dispozici
velmi kvalitně zpracované jízdní řády ve standardním formátu GTFS (o kterém
bude řeč níže) pro celou síť Pražské integrované dopravy (PID). Existují dvě
verze, jedna publikovaná pražským dopravním podnikem (DPP), druhá organizací
ROPID, která má na starost organizaci PID. My se zaměříme na data z ROPIDu,
která jsou o něco úplnější, detailnější a lépe strukturovaná. Obsahují informace
o všech linkách PID – městských i příměstských, včetně vlaků. Jsou aktualizována
denně a obsahují i krátkodobé výluky a omezení provozu.
Zveřejnění těchto dat má zajímavou historii. Jan Cibulka, novinář Českého
rozhlasu, si v roce 2013 všiml informací o spojích DPP
v Mapách Google. Na základě zákona o svobodném přístupu
k informacím (který dává státním úřadům a firmám povinnost na žádost poskytnout
informace vztahující se k jejich činnosti) požádal DPP o kopii dat předávaných Googlu.
Obdržel GTFS dataset, který následně zveřejnil.
Zpráva se rychle roznesla a od té doby chodil na DPP každý měsíc rostoucí počet
žádostí o poskytnutí aktuálních dat, kterým bylo vždy vyhověno, ale
všechny žádosti o trvalý přístup k datům byly zamítány. Až v roce 2015 dopravní
podnik obrátil (asi je to přestalo bavit vyřizovat) a začal poskytovat údaje
pro trvalý přístup k aktuálním jízdním řádům. O něco později pak došlo
k oficiálnímu zveřejnění na webu. Verze od ROPIDu je čerstvou novinkou z roku
2019.
Liberec. GTFS data nabízí také Dopravní podnik měst Liberce a Jablonce
nad Nisou (DPMLJ). Na rozdíl od pražských dat obsahují pouze MHD v obou městech
(plus tramvajovou linku mezi Libercem a Jabloncem) a nikoli příměstské spoje.
Zbytek republiky. Pro linkovou dopravu a MHD v ostatních městech je hlavním zdrojem informací
Celostátní informační systém o jízdních řádech (CIS JŘ). Tento systém byl
vznikl v roce 2000 jako iniciativa ministerstva dopravy a všichni dopravci ve
veřejné linkové dopravě jsou ze zákona povinni nahrávat do něj své jízdní řády.
Provoz tohoto systému byl svěřen společnosti Chaps, která na základě těchto dat
provozuje známý vyhledávač spojení IDOS. Ovšem strojově zpracovatelná data o jízdních
řádech veřejně k dispozici nebyla a protože Chaps je soukromá firma, zákon o svobodném
přístupu k informacím na ni použít nešel. Teprve po několika letech a nátlaku velkých
společností (např. Seznam.cz) udělilo ministerstvo provozovateli povinnost data
zveřejňovat.
Struktura dat a použité formáty v CIS jsou trochu nezvyklé. K dispozici jsou
tři velké balíky dat:
- První obsahuje data o autobusech, linkových i městských, ve formátu JDF (vytvořeném
pro potřeby CIS, nikde jinde se nepoužívá).
- Druhý obsahuje informace o trolejbusových a tramvajových provozech napříč celou
republikou, také ve formátu JDF.
- Třetí obsahuje informace o vlacích v XML formátu vycházejícím z evropského standardu
TAP TSI.
Odkaz na jednotlivé datové soubory najdete na stránce seriálu.
Takže pokud byste chtěli vyhledávat spojení např. v brněnské MHD, musíte si z jednoho
balíku vyzobat správné jízdní řády tramvají a trolejbusů, z druhého autobusy a případně ještě
z třetího (v úplně jiném formátu) městské vlaky. Ucelené jízdní řády MHD
v jednotlivých městech či integrovaných dopravních systémů jednotlivých krajů
k dispozici nejsou.
Formát CSV
Nejprve si stručně povíme o formátu CSV (comma-separated values), na kterém jsou
založené GTFS i JDF. CSV je jednoduchý formát pro reprezentaci dvourozměrné tabulky
textovým souborem. Každý řádek souboru představuje jeden řádek tabulky a jednotlivé
sloupce jsou odděleny čárkou (případně jiným znakem, často potkáte třeba středník
nebo tabulátor).
Pokud text v nějakém sloupci obsahuje čárku, je uzavřen do uvozovek.
Některé CSV soubory mají na prvním řádku hlavičku s názvy sloupců – potom nezáleží
na pořadí sloupců a můžete se orientovat podle názvů. To platí třeba pro GTFS. Naopak
JDF obsahuje CSV soubory bez hlavičky, takže musíte vědět, kolikátý sloupec co znamená.
Pokud si chcete CSV soubor manuálně prohlédnout, můžete ho kromě textového editoru
otevřít taky většinou tabulkových kalkulátorů, jako např. LibreOffice Calc.
V Pythonu lze CSV soubory načíst pomocí modulu csv
– třídy DictReader pro soubory s hlavičkami a reader pro soubory bez hlaviček.
Formát GTFS
GTFS (General Transit Feed Specification) je formát vytvořený společností Google.
Původně byl vytvořen, aby v něm poskytovali dopravci informace o spojích pro vyhledávač
spojení v Mapách Google. Ale postupně se z něj stal docela rozšířený standard.
Základní struktura GTFS je tvořena několika typy objektů popsanými níže. Každý objekt
má jednoznačný identifikátor (ID), pomocí kterého se na něj můžou jiné objekty odkazovat
(a jinak nemá obvykle žádný význam). Pokud jste se někdy potkali s cizími klíči v SQL
databázích, tohle je velmi podobný princip.
GTFS balík s jízdními řády (zvaný feed) je ZIP archiv plný CSV souborů. Až na pár
výjimek každý soubor popisuje objekty určitého typu, jeden na řádek, kde sloupečky jsou
jednotlivé vlastnosti. První řádek souboru obsahuje názvy sloupečků.
V GTFS potkáme následující druhy objektů.
Zastávky (stops.txt).
Každý záznam ve stops.txt má jednoznačný identifikátor (stop_id), název
(stop_name) a zeměpisné souřadnice (stop_lat, stop_lon).
Navíc obsahuje parametr location_type, kterým je rozlišeno několik druhů záznamů:
- 0: Stanoviště – tedy konkrétní místo, kde může vozidlo zastavit. Například
běžná nepřestupní zastávka je typicky tvořena dvěma stanovišti: na každé straně
ulice jedno pro jeden směr. U přestupních uzlů je typicky rozmístěno více stanovišť
třeba kolem jedné křižovatky, kde každé má svůj identifikátor, i když typicky sdílí
název zastávky. Více stanovišť najdeme taky třeba na autobusových nádražích, kde
každé je typicky označené nějakým číslem či písmenem. V přední části každého stanoviště
je obvykle umístěna dopravní značka, které se říká označník či zastávkový
sloupek, na které bývají navíc umístěné jízdní řády. Občas se pojem označník
či sloupek přeneseně používá i pro stanoviště jako celek.Stanoviště může
obsahovat ve sloupečku
parent_station ID uzlu (viz dále), ke kterému patří, a ve sloupečku
platform_code veřejné označení stanoviště v rámci uzlu (např. číslo/písmeno).
Zeměpisné souřadnice u stanoviště obvykle udávají přesnou polohu označníku, tedy
předního konce stanoviště.
- 1: Stanice nebo uzel – představuje skupinu stanovišť, které logicky nějak
„patří k sobě“. V případě jednoduché nepřestupní zastávky budou uzel tvořit dvě
protisměrná stanoviště, v případě přestupního uzlu všechna stanoviště, která jsou
soustředěná blízko sebe na jednom místě a lidé mezi nimi běžně přestupují. Uzel
může taky seskupovat všechna stanoviště v rámci autobusového či vlakového nádraží
společně se zastávkami MHD před nádražím.
- 2: Vchod/východ – udává pozici vstupu z ulice do prostor stanice, pokud
stanoviště není přímo na ulici. Nejčastěji potkáte u vstupů do metra, případně
vchodů do nádražní budovy. Opět pomocí
parent_station přiřazen ke stanici.
- 3: Obecné místo – popisuje další místa uvnitř stanic, která nejsou ani
stanoviště, ani vchody – např. různé vestibuly a chodby. Dá se použít pro navigaci
uvnitř stanic společně s
pathways.txt.
- 4: Nástupní oblast – popisuje část nástupiště. Dlouhá nástupiště typicky
bývají rozdělena na více oblastí. Ve spolupráci s
pathways.txt se dá použít
například k tomu, abyste poznali, že z jednoho konce soupravy metra je to blíž
ke konkrétnímu výstupu než druhého a třeba to mohli zohlednit v čase potřebném
na přestup.
Zmiňovaný soubor pathways.txt popisuje cesty mezi body uvnitř stanic – tedy
v zásadě hrany grafu, jehož vrcholy jsou body uvnitř stanic (stanoviště, vchody,
obecná místa, nástupní oblasti). Každá hrana obsahuje identifikátory vrcholů na obou
koncích (from_stop_id, to_stop_id), odhadovaný čas chůze v sekundách
(traversal_time), druh cesty (pathway_mode, např. 1=chodba, 2=schody,
4=eskalátor, 5=výtah), příznak obousměrnosti (is_bidirectional) a případně
informaci o tom, jaký nápis hledat na cedulích, když chce člověk jít daným
(signposted_as) či opačným (reversed_signposted_as) směrem. Standard
umožňuje popsat i spoustu dalších věcí, jako například počet
schodů či minimální průchodnou šířku, my se omezili na ty, které jsou v datech PID.
Body ve stanicích můžou mít také atribut level_id (odkazující se do levels.txt)
udávající, v jaké úrovni nad/pod zemí se daný bod nachází.
Podívejme se ještě krátce na specifika zastávek v pražských datech. Zastávky
povrchové dopravy jsou reprezentovány záznamy typu stanoviště, které nemají
vyplněný atribut parent_station. Sdružení zastávek do uzlů poznáme podle
jejich stop_id, který má tvar UčísloZčíslo[pásmo],
kde první číslo identifikuje uzel a druhé stanoviště v rámci uzlu. Na konci můžou
být ještě nějaké znaky upřesňující tarifní pásmo. Podle čísla uzlu můžeme zastávky
seskupit do uzlů.
U stanic metra vypadá situace trochu jinak. Každá má dvě stanoviště (pro každý směr jedno,
resp. čtyři v případě přestupních stanic),
dále k ní existuje záznam typu stanice s identifikátorem UčísloS1,
záznamy popisující vstupy (UčísloS1Ečíslo), záznamy popisující
vnitřní strukturu stanic (vestibuly a chodby, UčísloNčíslo).
Všechny záznamy patřící k dané stanici metra mají nastavený parent_station.
Stanice metra typicky sdílí číslo uzlu se zastávkami povrchové dopravy v její blízkosti,
ale ty už parent_station nastavené nemají.
Železniční stanice jsou popsané jen jedním vrcholem typu stanoviště, nástupiště se nerozlišují.
Trasy spojů (viz níže) se odkazují pouze na stop_id typu stanoviště.
Na stránkách ROPIDu je navíc k dispozici podrobný seznam zastávek s detaily,
které se do GTFS nevešly. K dispozici je ve formátu JSON (načtete v Pythonu
triviálně pomocí modulu json) nebo XML. Struktura je dobře zdokumentovaná
přímo tam, takže zde nebudeme opakovat.
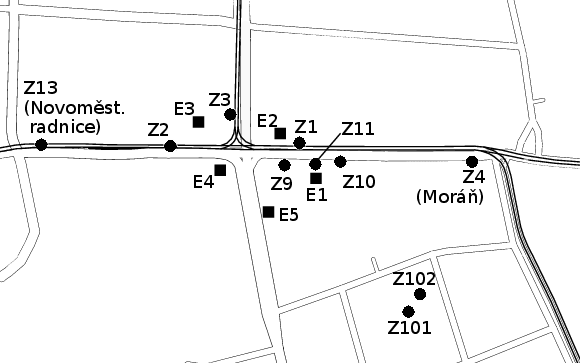
Vše si ukážeme třeba na příkladu přestupního uzlu U237 Karlovo náměstí, kde
uvádíme jen zkrácené identifikátory (např. Z1 místo U237Z1P
či E1 místo U237S1E1):
Z1 až Z3 jsou tři tramvajová stanoviště nesoucí název Karlovo náměstí, kde
staví tramvaje jedoucí různými směry. Z4 a Z13 jsou tramvajové zastávky o kus
dál, které oficiálně pro cestující mají jiné názvy (Moráň a Novoměstská
radnice), ale interně jsou považovány za součást stejného uzlu. Obě jsou
jednosměrné (staví tam jen tramvaje ve směru od Karlova náměstí), proto mají
jen jedno stanoviště. Například linka 22 zastaví v jednom směru na Z3 a pak
Z13, v druhém jen na Z2.
Z101 a Z102 jsou stanoviště metra B (pro každý směr jedno). Jejich poloha
zhruba odpovídá tomu, kde se pod zemí skutečně nachází prostředek nástupiště.
E1 až E5 jsou vstupy do metra.
Z9, Z11 a Z10 jsou tři autobusová stanoviště ležící u jedné nástupní hrany
těsně za sebou, ale každé má svůj označník a staví u něj trochu jiné linky.
K tomuto uzlu patří ještě vstupy do metra (E6 až E8) a tramvajové zastávky
(Z5 až Z8) na Palackého náměstí, které už se nám do mapky nevešly. Též nezobrazujeme
body popisující vnitřní strukturu stanice metra. Celkem uzel obsahuje 12 stanovišť
povrchové dopravy, 2 stanoviště metra, 9 vstupů do metra, 19 pomocných bodů ve stanici
metra a 1 záznam pro stanici metra jako celek.
Největší vzdálenost v tomto uzlu je mezi
stanovišti Novoměstská radnice a Palackého náměstí, 700 metrů chůze. Na tom je
vidět, že příslušnost ke stejnému uzlu je jen velmi hrubým měřítkem toho, mezi
kterými stanovišti lze rychle a pohodlně přestoupit.
Spoje (trips.txt). Každý spoj popisuje jednu cestu vozidla na
nějaké lince z konečné na konečnou v nějakém konkrétním čase. Soubor
trips.txt obsahuje základní informace o spojích (jeden řádek na spoj):
trip_id je jednoznačný identifikátor spoje, route_id je
identifikátor linky, ke které spoj patří, a service_id je identifikátor
kalendáře udávajícího, ve které dny spoj jezdí (např. „pondělí a pátky
kromě 24.12.“).
Dále je u každého spoje popsaná jeho trasa – v zásadě posloupnost trojic
(identifikátor zastávky, čas příjezdu, čas odjezdu). Každé takovéto trojici
budeme říkat jedno zastavení daného spoje. Trasy spojů se nachází v samostatném
souboru stop_times.txt. Každý řádek představuje jedno zastavení nějakého
spoje. Obsahuje následující položky:
trip_id – identifikátor spojestop_sequence – pořadí toho zastavení na trase spoje (počítá se od jedničky,
číslování nemusí být souvislé, na fyzickém pořadí řádek v souboru nezáleží)arrival_time a departure_time – čas příjezdu a odjezdu (textově
ve formátu hh:mm:ss, v místní časové zóně), u spojů jedoucích přes půlnoc potkáme
časy jako třeba 24:15:00stop_id – identifikátor zastávky (v případě pražských dat přesněji
identifikátor stanoviště)
Všimněte si, že u každého spoje je uvedena jeho kompletní trasa – formát nijak
nepředpokládá, že např. všechny spoje na nějaké lince mají stejnou trasu. To ani
v praxi mít nemusí: např. některé spoje jedou jen zkrácenou část trasy linky,
spoje zatahující do vozovny mají nestandardní trasu, u některých linek je třeba
část trasy v jednom směru odlišná od opačného směru atd. I když mají spoje na
lince stejnou trasu, často se třeba v různých denních dobách liší jízdní doby
(podle intenzity dopravy).
Při hledání spojení je obvykle nejjednodušší zapomenout na to, že nějaké linky
existují a pracovat pouze s jednotlivými spoji. Informace o lince se stále
hodí, např. k tomu, abychom ji mohli zobrazit uživateli (a ten věděl, do čeho
má nastoupit).
Linky (routes.txt). U linek nás bude zajímat jen pár základních
údajů:
-
route_id – jednoznačný identifikátor linky
-
route_short_name – veřejné označení linky, typicky číslo linky
(resp. u metra písmeno, můžou se vyskytnout i jiné speciality typu linky H1
pro přepravu vozíčkářů)
-
route_type – typ vozidla. V PID potkáte: 0=tramvaj, 1=metro, 2=vlak, 3=autobus,
4=přívoz, 7=kolejová lanovka (na Petřín), 800=trolejbus (tohle je lokální konvence, GTFS
nemá standardní kód pro trolejbusy)
Kalendáře (calendar.txt). Každý kalendář
určuje množinu dnů, ve kterých spoje s tímto kalendářem jezdí. Základní vymezení
kalendáře je pomocí rozsahu dat, kdy spoje jezdí (od start_date do end_date)
a dnů v týdnu, ve kterých jezdí (sloupečky monday až sunday obsahující
hodnoty 0/1). Navíc lze do kalendáře přidávat výjimky pro konkrétní data (např. státní
svátky). Ty jsou uvedené v souboru calendar_dates.txt, každý řádek popisuje jednu
výjimku: service_id je identifikátor kalendáře, na který se vztahuje, date
je konkrétní datum a exception_type je 1=spoje v tento den výjimečně jedou,
2=spoje v tento den výjimečně nejedou (oproti pravidelnému kalendáři).
Specialitou pražských dat je, že jsou vydávána pouze na týden dopředu, takže i výjimky
v kalendáři najdete jen pro následující týden.
XML formát pro vlaky
Poznámka: pro vaše pohodlí jsme napsali skript pro převod z XML formátu do GTFS. Skript
i výsledné vlakové GTFS najdete na stránkách seriálu. Tedy pokud chcete, můžete tuto
kapitolu přeskočit. Ale pokud jste zvědaví, pokračujte dál.
Balík s vlakovými jízdními řády je ZIP archiv plný XML souborů. Každý soubor popisuje
jeden spoj a jeho trasu. O zpracování XML už byla řeč v předchozích dílech seriálu,
teď to bude trochu jednodušší, protože se vám celý dokument vejde do paměti.
Většinu pro nás důležitých informací se skrývá uvnitř prvku <CZPTTInformation>,
(který je potomkem kořenového prvku <CZPTTCISMessage>). <CZPTTInformation> má:
- Jednoho potomka
<PlannedCalendar> popisujícího, ve které dny vlak jezdí.
- Více potomků
<CZPTTLocation>, které dohromady popisují trasu vlaku. Každý představuje
jeden bod na trase vlaku.
Překvapivě některé základní údaje, jako třeba druh nebo číslo vlaku, jsou uvedené u každého
bodu trasy. Existují totiž třeba vlaky, které po cestě změní číslo nebo se promění z rychlíku
na osobní vlak, byť jich není mnoho.
Kalendář vlaku. Narozdíl od GTFS se zde vůbec neoperuje s dny v týdnu.
Prvek <ValidityPeriod> s potomky <StartDateTime> a
<EndDateTime> udává základní rozsah dat, ve kterém vlak jezdí.
Data jsou uvedena ve formátu např. 2020-11-01T00:00:00. Časová složka
je vždy 00:00:00 a nenese žádný význam. Obě koncová data jsou včetně.
To je trochu matoucí, protože když je <EndDateTime> 2020-11-01T00:00:00,
vlak 1.11. ještě naposledy jede, přestože zápis vypadá, jako by provoz o půlnoci
končil.
V rámci svého rozsahu platnosti může vlak jet jen v některé dny. To je určeno prvekm
<BitmapDays>. Ten obsahuje řetězec jedniček a nul stejně dlouhý jako rozsah
platnosti vlaku. Přitom k-tý znak tohoto řetězce udává, jestli vlak jede k-tý den svého
rozsahu platnosti.
Existují i speciální vlaky, které jedou jen jeden den v roce. Ty mají uvedený ve
<StartDateTime> datum jízdy, v <BitmapDays> řetězec 1
a <EndDateTime> úplně chybí.
Některé vlaky mají v určité dny jinou trasu – např. zkrácenou či prodlouženou
či vynechávají nějakou zastávku (třeba v chatařské osadě staví jen o víkendech
v létě). To tento formát neumí reprezentovat, takže je prostě příslušný vlak
uvedený dvakrát (ve dvou různých XML souborech), pokaždé s jinou trasou a
rozsahem platnosti, ale stejným číslem.
Trasa vlaku. Trasa vlaku je zapsána posloupností prvků CZPTTLocation.
Každý z nich udává nějaké místo na trase vlaku (typicky stanici nebo zastávku,
ale občas se objeví i nějaká interní provozní místa, např. „Brno hl.n. přednádr.“).
Na trase mohou být uvedena nejen místa, kde vlak staví, ale i místa, kterými projíždí.
U každého místa je uveden plánovaný čas příjezdu a odjezdu (resp. průjezdu). Narozdíl
od GTFS je pořadí bodů na trase dáno jejich pořadím v XML souboru.
Prvek CZPTTLocation má následující potomky:
-
<PrimaryLocationName> – název stanice (či zastávky). Z historických důvodů
se některé názvy uvádí zkrácené, např. „Praha Masaryk.n.“ či „Jablonec n.N. dol.n.“
-
<LocationPrimaryCode> – číslo stanice v číselníku SR 70 (viz níže), pětimístné
bez kontrolní číslice. Pomocí něj lze dohledat další informace o stanici, např. plný
název či zeměpisné souřadnice. Ve vlakových jízdních řádech se nerozlišují jednotlivá
stanoviště (nástupiště, staniční koleje), protože se obvykle přidělují dynamicky za provozu. Kód
tedy identifikuje stanici jako celek.
-
<OperationalTrainNumber> – číslo vlaku platné počínaje touto stanicí (jen číselná
část, neobsahuje druh vlaku).
-
<TrafficType> – druh vlaku (11=osobní, C3=spěšný, C2=rychlík, C1=expres – sem obvykle
patří i další vlaky vyšší kvality, např. EC, IC, SC)
-
<CommercialTrafficType> – číslo vyjadřující tzv. komerční druh vlaku
(Os, R, IC, SC, RJ, ...), tedy to, co se obvykle uvádí jako součást čísla vlaku
(např. „SC 507“). Např. 84=Os, 157=R, 63=IC, 50=EC, ... Více
hodnot se dá najít na stránkách seriálu.
-
<TimingAtLocation> udává časy příjezdu a odjezdu. Jeho potomky jsou prvky
<Timing> s rolí danou atributem TimingQualifierCode. ALA znamená
čas příjezdu a ALD čas odjezdu. Některý z nich může chybět, například konečná
stanice nemá čas odjezdu. V případě průjezdu či krátkého zastavení bývají oba časy
shodné. Časy jsou uvedené ve tvaru 15:00:00.0000000+01:00. Část +01:00
je časové pásmo, u nás ho můžeme ignorovat a vše považovat za místní čas.
-
<TrainActivity> popisuje tzv. „aktivity“ vlaku v daném místě, což znamená
např. informace o zastavování vlaku a (ne)čekání na přípoje. Může obsahovat jeden nebo
více potomků <TrainActivityType>, každý z nich nese číselný kód popisující
jednu aktivitu. Důležité kódy: 0001 = vlak v dané stanici zastavuje (pokud není uvedeno,
stanici projíždí), 0028 = zastavení jen pro nástup, 0029 = zastavení jen pro výstup (obojí
uváděno spolu s 0001). Pokud vlak stanicí projíždí, prvek <TrainActivity>
může zcela chybět.
-
<ResponsibleRU> udává kód dopravce vlaku počínaje touto stanicí (ano, i dopravce
se může po cestě vlaku změnit, typicky se to stává u mezinárodních vlaků, které na území
každé země formálně provozuje jiný dopravce). Seznam dopravců a postup k jeho získání
najdete na stránkách seriálu.
Číselník stanic SR 70 je dlouhá tabulka obsahující seznam všech stanic, zastávek
a dalších významných míst v české
železniční síti, tak trochu obdoba souboru stops.txt v GTFS. Dá se stáhnout
ze stránek Správy železniční dopravní cesty (SŽDC) ve formátu XLSX, který se dá třeba
pomocí LibreOffice zkonvertovat do CSV a pak s ním jde rozumně pracovat. Na stránkách
seriálu najdete už zkonvertovaný. Zajímavé sloupečky jsou:
-
SR70 – číselný kód místa. Je to šesticiferné číslo, kde poslední číslice
je kontrolní a dá se spočítat z předchozích. V XML jízdních řádech je jen prvních
pět číslic, takže při porovnání je třeba poslední číslici zahodit.
-
Tarifní název – plný název
-
GPS X, GPS Y – zeměpisná délka a šířka
Pokud použijete naše vlakové GTFS, v něm už jsou informace ze SR 70 a číselníku dopravců
zahrnuté, takže je nemusíte shánět zvlášť.
Formát JDF aneb celostátní informační chaos
Formát JDF zde popisujeme pro úplnost, kdybyste si třeba chtěli hrát s jízdními řády
ve svém oblíbeném městě, ale k řešení úloh ho potřebovat nebudete.
Soubor, který si stáhnete z CIS JŘ, je ZIP archiv, který obsahuje hromadu několik stovek
až tisíc vnořených ZIP archivů – pro každou linku jeden. Asi je nechcete rozbalovat ručně
jeden po druhém, místo toho doporučujeme v Pythonu modul zipfile,
který umí se ZIP soubory zacházet programově. Taky se vám může hodit funkce os.listdir
pro vypsání obsahu adresáře. Alternativně můžete archivy rozbalit pomocí unixového shellu
(o kterém byla řeč v seriálu 27. ročníku), například takovýmto příkazem:
for file in *.zip; do
unzip $file -d $(basename $file .zip)
done
Podívejme se nyní na obsah jednoho linkového ZIP archivu. Strukturou se podobá GTFS
– obsahuje několik CSV souborů, které popisují např. zastávky nebo spoje. Na rozdíl
od GTFS jsou to CSV bez hlavičky, navíc je ještě na konci každého řádku středník.
Jsou uložené v kódování CP1250 namísto
standardního UTF-8. V Pythonu můžete při otvírání souboru určit kódování takto:
open("soubor.txt", "r", encoding="windows-1250"). Aktuálně se používají čtyři
různé verze JDF: 1.8 až 1.11, které se liší počtem a občas i pořadím sloupců (občas
je v nějaké verzi vložen nový sloupec doprostřed, takže všemu za ním se posune číslo
sloupce). Dokumentaci k jednotlivým verzím lze najít v metodických pokynech
ministerstva dopravy, na které odkazujeme ze stránky seriálu.
Protože načítání takovýchto souborů je velmi nepohodlné, připravili jsme pro vás
verzi v našem vlastním formátu „JDF-H“. Ten se liší několika věcmi:
- Všechny CSV soubory mají hlavičky s názvy sloupců
- Soubory mají kódování UTF-8 a unixové konce řádků
- Na konci řádků nejsou středníky
- V ZIP archivu jsou podadresáře místo vnořených ZIPů
Na stránce seriálu si můžete stáhnout jak výsledné soubory, tak převodní skript.
Podívejme se nyní na některé ze souborů. U sloupců budeme uvádět názvy používané v JDF-H.
Zastavky.txt. V tomto souboru najdete seznam zastávek, které daná linka používá.
CisloZastavky je identifikátor zastávky, unikátní v rámci dané linky. Pomocí
něj se na zastávku odkazují spoje v rámci linky. Zastávky nemají žádné globálně jednoznačné
identifikátory. Že více linek staví na téže zastávce, poznáte víceméně jen podle názvu,
a to ne úplně spolehlivě, protože názvy zastávek také nejsou jednoznačné.
Sloupce NazevObce, CastObce, BlizsiMisto dohromady určují název
zastávky (BlizsiMisto je upřesnění místa, třeba nám. nebo žel.st.).
Takovéto rozdělení názvu na tři části je dodržované hlavně v linkové autobusové dopravě, kde jsou stejným
způsobem (de facto „jako CSV“) uváděné názvy zastávek i na papírových
jízdních řádech a zastávkových označnících. Taky vám přišlo divné, proč názvy
autobusových zastávek občas obsahují dvě čárky za sebou (např. „Klatovy,,aut.nádr.“)?
V MHD se tato konvence příliš nedodržuje – zastávky mají typicky názvy unikátní
v rámci celého města a sloupec CastObce se nechává prázdný. Občas ale narazíme
na různé nesrovnalosti, nahodilé i systematické. Občas je například název zastávky
ve sloupci CastObce namísto BlizsiMisto. A třeba v plzeňské MHD je
dokonce ve sloupci NazevObce a ostatní jsou prázdné (poslední příklad).
Příklady:
| NazevObce | CastObce | BlizsiMisto |
|
Hrochův Týnec | | nám. |
|
Ostrava | Vítkovice | Mírové nám. |
|
Praha | Zličín | |
|
Praha | ÚAN Florenc | |
|
Praha | | ÚAN Florenc |
|
Praha | | Karlovo náměstí |
|
Brno | Královo Pole | nádraží |
|
Brno | | Tylova |
|
Brno | Tylova | |
|
Západočeská univerzita | | |
Problém s párováním zastávek podle názvu je, že názvy obcí a jejich částí nejsou
unikátní. Skoro unikátní je kombinace název obce + okres (až na dvě výjimky), ale
okresy u zastávek nenajdeme. Taktéž u zastávek nejsou uvedené zeměpisné souřadnice.
Pokud si z JDF vybereme jen MHD v jednom konkrétním městě, asi se můžeme spolehnout
na jednoznačnost názvů zastávek. Protože nemáme informace o poloze zastávek, hůře
se řeší přestupy. Ale v první aproximaci můžeme prostě dovolit přestupy mezi zastávkami
stejného jména a určit nějaký fixní čas na přestup. Pokud bychom chtěli být přesnější,
můžeme zkusit získat informace o pozicích zastávek z OpenStreetMap, více o tom později.
V případě linkové dopravy se na jednoznačnost názvů spolehnout nemůžeme. Asi jediná
naděje je zkoušet nějak heuristicky párovat zastávky na zastávkové body v OpenStreetMap.
Například pokud na trase linky jsou alespoň nějaké zastávky či obce s jednoznačným názvem,
můžeme pak u nejednoznačných zastávek vybrat ty, které jsou rozumně blízko těm známým,
aby trasa spoje dávala smysl. U vnitrokrajských linek nám navíc může pomoci informace
o kraji, kterou lze vyčíst z první číslice šestimístného čísla linky. Má to i další
háčky, například v OpenStreetMap pravděpodobně nejsou všechny zastávky, případně
můžou mít názvy drobně odlišné od těch používaných v CIS.
V případě názvů obcí se asi dá věřit, že budou ve většině případů stejné v OSM i CIS.
Takže jedno možné řešení by mohlo být heuristicky určit jednoznačné identifikátory
obcí na trase (podle názvu a v případě nejednoznačností podle blízkosti ke zbytku
trasy) a jako zastávky identifikovat trojicí (jednoznačný identifikátor obce,
název části obce, upřesnění místa).
Ale přiznávám, že jsem strávil přes dva týdny neúspěšnými pokusy upravit data do
použitelné podoby (což je jeden z důvodů zpoždění seriálu, za které se omlouváme).
Linky.txt – tento soubor obsahuje jediný řádek s informacemi o lince.
Některé zajímavé sloupce:
-
CisloLinky – šestimístné, celostátně unikátní. V případě linkových autobusů
toto číslo vidíte v jízdním řádu. U městské dopravy je to jen interní identifikátor
a veřejné (krátké) číslo linky najdete v souboru LinExt.txt.
-
NazevLinky – lidsky čitelný název linky, např. „Brno – Jihlava – Praha“
-
ICDopravce – číslo dopravce z Dopravci.txt
-
TypLinky – A=městská, B=příměstská, V=vnitrokrajská, Z=mezikrajská, D=dálková,
N/P=mezinárodní
-
DopravniProstredek – A=autobus, E=tramvaj, L=lanovka, M=metro, P=přívoz, T=trolejbus
-
PlatnostJROd, PlatnostJRDo – platnost jízdního řádu. Linka může mít víc různých verzí, které mají stejné
číslo linky, ale liší se platností (každá verze se nachází v samostatném ZIPu). Občas se v datech
z nějakého důvodu vyskytnou dvě verze linky s překrývajícím se rozsahem platnosti. V takovém
případě není definováno, který má přednost, ale pravděpodobně většinou ten s pozdějším začátkem
platnosti.
LinExt.txt (JDF 1.10+) – obsahuje dodatečné informace o lince. KodDopravy je identifikátor
systému MHD či integrovaného dopravního systému (IDS), ke kterému linka patří. Možné hodnoty nejsou
oficiálně zdokumentované, ale vytvořili jsme pro vás seznam, který najdete na stránkách seriálu.
Podle tohoto sloupečku lze snadno z JDF vyfiltrovat linky MHD daného města (ve starších verzích
JDF možná pomůže filtrovat podle dopravce).
OznaceniLinky je „krátké“ číslo linky používané v rámci daného systému MHD.
Spoje.txt – popisuje seznam spojů na lince. CisloSpoje je pořadové číslo spoje
v rámci dané linky. PevKod1 až PevKod10 jsou čísla tzv. pevných kódů
udávající omezení jízdy spoje (např. „jede v pracovní dny“). Z nějakého neznámého důvodu
se tady neuvádějí značky s pevně definovaným konkrétním významem. Namísto toho jsou tady uvedena
nějaká zcela obecná čísla, kterým je přiřazen význam v souboru Pevnykod.txt. Čísla pevných
kódů můžou být na každé lince úplně jiná. Další omezení jízdy spojů můžou být dána časovými kódy,
o nich později.
Zasspoje.txt – popisuje trasy jednotlivých spojů. Zajímavé sloupce:
-
CisloSpoje (ze Spoje.txt)
-
CisloZastavky (ze Zastavky.txt)
-
CasPrijezdu, CasOdjezdu – obsahují časový údaj ve formátu hhmm (např. 1745),
nebo znak |, pokud spoj zastávkou projíždí, nebo znak >, pokud spoj kolem zastávky ani nejede
(ale jiné spoje na lince ano). Čas příjezdu může chybět, pokud je stejný jako čas odjezdu.
Geografická data o zastávkách
Jak už jsme zmínili, JDF neobsahuje informaci o zeměpisné poloze zastávek. Tu
lze získat z několika míst. Jedním z nich je OpenStreetMap, se kterou jste se
seznámili v předchozích dílech seriálu. Popis zastávek v OSM je trochu
komplikovaný a existuje více způsobů, jak zastávky reprezentovat v OSM datech.
Také v OSM je odhadem jen zhruba polovina českých zastávek, nejlepší pokrytí je
ve větších městech.
Dalším zdrojem dat jsou krajské a městské úřady, které často mají vlastní mapu
zastávek. Některé z nich je zveřejňují jako otevřená data (například jihočeský
a královehradecký kraj, které tímto mají naši poklonu), od jiných se nám je
podařilo získat žádostí podle zákona o svobodném přístupu k informacím. Tato
data jsou v dost různorodých formátech.
Pokusili jsme se dát dohromady data ze všech dostupných zdrojů a převést je do
jednotného formátu, více informací najdete na stránkách seriálu.
Reprezentace pomocí stavového prostoru
(Většina této sekce je převzata z řešení úlohy 28-2-6 Cesta MHD.)
Abychom v jízdních řádech mohli vyhledávat spojení, hodilo by se nám je
reprezentovat grafově. Zkusme si tedy vytvořit graf popisující naši síť,
takový, že cesty v něm budou odpovídat korektním spojením v daném jízdním řádu.
Určitě si nevystačíme s jednoduchým grafem, který má za vrcholy zastávky.
Protože na jednu zastávku můžeme během našeho putování přijet víckrát, taková
jízda by v našem grafu netvořila cestu, nýbrž sled (mohou se opakovat vrcholy).
Se sledy se obvykle špatně pracuje, zkusme to tedy jinak.
Vytvoříme si takzvaný stavový prostor. To je graf, jehož vrcholy
popisují nějaký stav (situaci), ve kterém se můžeme nacházet, a hrany
mezi nimi určují dovolené změny stavu. V našem případě budou stavy dvojice
(z, t) popisující „jsem na zastávce z v čase t“.
Aby se nám s časy lépe pracovalo, můžeme je místo hodin, minut a sekund
reprezentovat například jedním číslem udávajícím počet minut (resp sekund, dle
potřebné přesnosti) od půlnoci místního času. Aktuálně má v ČR pouze pražské
metro plánované odjezdy s přesností na sekundy (IDOS vám je neukáže, ale v GTFS
jsou a občas se tato přesnost při přestupování opravdu hodí).
V takovéto reprezentaci nelze hledat spojení přes půlnoc, to prozatím
zanedbejme.
Jak se takový
stav může změnit? Pokud v čase t odjíždí ze z nějaký spoj, jehož
nejbližší další zastávka je z', a přijede na ni v čase t', pak určitě
ze (z,t) povede hrana do (z',t'). Můžeme se tímto spojem svézt a tím
se ocitnout na zastávce z' v čase t', tedy ve stavu (z', t').
Ale nemusíme nastoupit do prvního spoje, který jede. Potřebujeme umět
reprezentovat i to, že počkáme na nějaký další. To by se dalo udělat
například tak, že vždy ze (z,t) povede hrana do (z,t+1). Pak bychom
ale u každé zastávky museli mít vrcholy pro všechny možné časy, což by
bylo neúsporné. Místo toho je vytvoříme jen pro ty časy, kdy v z něco
zastavuje. A hrany pak povedou vždy ze (z,t) do (z,t'), kde t' je čas
nejbližšího dalšího odjezdu/příjezdu po t.
Ukážeme si to na jednoduchém umělém příkladu, protože skutečné dopravní
sítě jsou příliš rozsáhlé a komplikované. Představme si následující
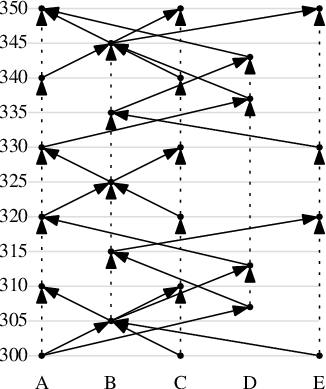
dopravní síť s pěti zastávkami označenými A až E:
Síť je tvořena dvěma linkami, X (plná čára, jezdí každých 20 minut v trase
A–B–C a opačně) a Y (čárkovaná čára, jezdí každých 30 minut v trase
A–D–B–E a opačně). Čísla na hranách značí jízdní dobu mezi příslušnými
zastávkami.
Část jízdního řádu této sítě pro dobu mezi pátou a šestou hodinou (časy 300 a
360 – počítáme v minutách) by mohla vypadat takto (jeden řádek představuje
jeden spoj):
A 300 B 305 C 310
A 320 B 325 C 330
A 340 B 345 C 350
C 300 B 305 A 310
C 320 B 325 A 330
C 340 B 345 A 350
A 300 D 307 B 315 E 320
A 330 D 337 B 345 E 350
E 300 B 305 D 313 A 320
E 330 B 335 D 343 A 350
Pro tento kousek jízdního řádu bude příslušná část stavového grafu vypadat
takto:
Tečkované hrany odpovídají čekání na zastávce, plné přesunům vozidly.
Minimální čas na přestup
Naše reprezentace má jednu podstatnou nevýhodu: dovoluje cesty s nulovým časem
na přestup. Můžeme např. v čase 305 přijet linkou X do zastávky B a ve stejný
okamžik zase odjet linkou Y do D. To není moc realistické. I přestup v rámci
jednoho stanoviště nějakou chvíli trvá a navíc si nejspíš chceme nechat časovou
rezervu pro případ zpoždění prvního spoje (přesuny mezi stanovišti a čas
potřebný pro ně teď neuvažujeme, k těm se vrátíme později).
Rádi bychom tedy vynutili minimální čas na přestup: pokud přijedeme do zastávky
nějakým spojem v čase t, můžeme přestoupit na jiný spoj, pouze pokud odjíždí
v čase t+λ nebo později, pro nějakou konstantu λ (v principu
to nemusí být konstanta, požadovaný čas může záviset třeba na konkrétní zastávce
či denní době).
Tady je náš dosavadní stavový prostor neadekvátní. Protože to,
kam můžeme pokračovat např. z vrcholu (B, 305) záleží na tom, kudy
jsme do něj přijeli. Pokud jsme přijeli z vrcholu (A,300) spojem linky X,
můžeme například pokračovat dál stejným spojem do vrcholu (C,310).
Ale pokud jsme přijeli z (E,300) linkou Y, do (C,310) se vydat
nemůžeme, protože bychom museli v B přestoupit s nulovou rezervou.
To je v přímém rozporu se základním principem stavových prostorů:
možné akce jsou vždy jednoznačně určené vrcholem, ve kterém se nacházíme.
Namísto původní hrubé informace „jsem na zastávce z v čase t“
se budeme muset naučit rozlišovat mezi stavy „stojím na zastávce z
(venku) v čase t“ a „jsem ve vozidle spoje s, které právě
zastavilo na z v čase t“. Tedy stav bude popsán trojicí (z,t,s),
kde s je identifikátor spoje nebo „-“ reprezentující „stojím venku“.
Zbývá správně natahat hrany. Čekací hrany povedou jen mezi
„venkovními“ vrcholy, tedy ze (z,t,-) do (z,t',-), kde t'
je opět čas nejbližšího dalšího odjezdu/příjezdu. Zároveň přidáme hrany
popisující nástup do vozidla: pro vozidlo spoje s odjíždějící ze z
v čase t přidáme hranu (z,t,-) →(z,t,s). Ještě celkem
přímočaré budou hrany popisující cestu ve vozidle: pokud spoj s jede
ze z (odj. t) do z' (příj. t'), přidáme hranu
(z,t,s) →(z',t',s).
Hlavní trik spočívá ve hranách popisujících výstup z vozidla. Ty budou
mít tvar (z,t,s) →(z,t+λ,-). Můžeme si to
představovat tak, že každé vozidlo
na zastávku přijede λ minut po tom, co z ní odjede. Případně
pokud je to na vás příliš sci-fi, můžete si představit, že vám
λ minut trvá vystoupit z vozidla. Každopádně si snadno
rozmyslíte, že touto úpravou zařídíme dodržení času na přestup.
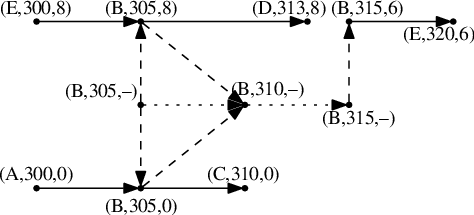
Malý kousek nového grafu ukazující přestupy v B okolo času 305
(pro λ= 5):
Tečkované hrany jsou opět čekací a plné jízdní, přibyly čárkované
nástupní a výstupní. V tomto grafu už se z (A,300) dostaneme do
(C,310), ale z (E,300) nikoli. V obou případech si navíc můžeme
v B počkat do 315, přestoupit na spoj 6 a pokračovat dál.
Sestrojit takovýto graf by mělo být celkem přímočaré, případně
je to popsané v řešení úlohy 28-2-6 včetně
ukázkového programu. Na stejném místě najdete ukázkovou aplikaci,
jak pomocí stavového grafu najít cestu, při které za den strávíte
co nejvíc času v dopravních prostředcích.
Pěší přesuny
Při přestupování mezi linkami MHD často musíme dojít pěšky z jedné
zastávky na jinou. Často to bývá jiné stanoviště v témže uzlu, ale
nemusí to platit vždy.
Pokud máme jízdní řád, který rozlišuje pouze uzly a ne jednotlivá stanoviště,
není moc co řešit. Pěší přestupy v rámci máme zajištěné automaticky a musíme
jen nastavit dostatečnou minimální dobu na přestup (viz předchozí oddíl).
Nevýhoda je, že nemůžeme rozlišit ani přestupy v rámci jednoho stanoviště a
mezi různými stanovišti – vždy budeme vyžadovat stejnou dobu na přestup. Co
můžeme, je nastavit různou přestupní dobu pro různé uzly, pokud se to hodí.
Potenciálně bychom mohli chtít ještě přidat možnost pěšího přesunu mezi dvěma
blízkými uzly, ale asi to bude potřeba spíš výjimečně.
O trochu zajímavější je to, pokud rozlišujeme jednotlivá stanoviště. Musíme
si odpovědět na dvě otázky: (1) mezi kterými dvojicemi stanovišť uvažovat
pěší přesuny, (2) pro každou dvojici určit čas potřebný na přesun.
První otázku můžeme řešit dvěma různými způsoby: pokud máme informace
o příslušnosti zastávek k uzlům, můžeme povolit přestupy pouze v rámci
jednoho uzlu (a tam uvážit všechny možné dvojice stanovišť). Obecnější
řešení je ignorovat uzly a vyjít z geografické polohy stanovišť (pokud
ji máme k dispozici). Pak prostě najdeme všechny dvojice stanovišť vzájemně
vzdálených méně než nějaká konstanta. Tady můžeme uvažovat velmi hrubý
odhad vzdálenosti: například vzdušnou čarou nebo v manhattanské metrice
(o ní víc níže).
Algoritmus pro nalezení všech dvojic blízkých bodů byl popsán například
v řešení úlohy 31-Z3-4.
Když už máme nějakou dvojici stanovišť, mezi kterými vypadá smysluplně
pokoušet se o pěší přesun, rádi bychom odhadli, jak dlouho to bude trvat.
První dobrý krok je asi odhadnout vzdálenost, kterou budeme muset ujít.
To by se dalo udělat například tak, že budeme hledat trasu mezi stanovišti
v mapě – například pomocí dat z OpenStreetMap. To je ale spousta práce.
Ve městech, kde typicky bývá víceméně pravoúhlá síť ulic, lze celkem
dobře aproximovat docházkové vzdálenosti pomocí tzv. manhattanské
vzdálenosti. Pokud máme ve čtvercové síti dva body o souřadnicích
(x1, y1) a (x2, y2), jejich manhattanská vzdálenost je rovna
|x2-x1| + |y2-y1| – tedy délka cesty, která by vedla nejdřív
jen vodorovně (západovýchodně) a potom jen svisle (severojižně).
Snadno
si ale rozmyslíte, že stejně dlouhé jsou i složitější cesty, dokud
chodíte jen vodorovně a svisle (ne šikmo) a nevracíte se zpátky. Tedy
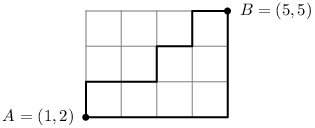
obě cesty znázorněné tučně na následujícím obrázku mají délku 7,
a to je manhattanská vzdálenost bodů A a B:
Zatímco manhattanská vzdálenost je celkem dobrým odhadem docházkové vzdálenosti
(pouze ve městech a pouze na kratší vzdálenosti), na základě docházkové
vzdálenosti není úplně jednoduché odhadnout docházkový čas. Při přestupování ve
městě někdy třeba strávíte víc času čekáním na přechodu než samotnou chůzí.
A to je věc, která se zohledňuje velmi těžko, protože závisí na intenzitě
automobilové dopravy, která navíc závisí na denní době…Asi jediné
jednoduché řešení je přidat k odhadnutému docházkovému času dostatečnou
rezervu.
Další zradou, na kterou je třeba si dát pozor, jsou různé překážky: jako třeba
řeka nebo skok v nadmořské výšce. Ty nepotkáte zas tak často, ale dá se na ně
nachytat. Například zastávka metra Vyšehrad (na konci Nuselského mostu) a
tramvajová zastávka Svatoplukova (dole v Nuselském údolí) mají manhattanskou
vzdálenost pouhých 220 metrů, ale výškový rozdíl 40 metrů a typicky mezi nimi
přestupovat nechcete. Zastávky Zlíchov a Dvorce mají manhattanskou vzdálenost
400 m, ale nejkratší pěší spojnice má 2,7 km přes Barrandovský most.
První problém dokážeme vyřešit porovnáním nadmořských výšek obou stanovišť.
V minulém díle jsme si ukázali použití výškových dat ze SRTM. Například
Praha má vlastní, přesnější výškový model,
ale jeho zpracování by bylo na delší povídání. Kdyby vás to zajímalo,
poradíme na fóru.
Alternativně oba problémy můžeme z velké části eliminovat tím, že povolíme
přestupy pouze v rámci uzlu (ale tím se připravíme potenciálně o nějaké
zajímavé nestandardní přestupy).
Výpočet manhattanské vzdálenosti
Pro body ve čtvercové síti je výpočet manhattanské vzdálenosti triviální
použitím vzorečku výše. Problém je, že povrch Země není čtvercová mřížka.
Pokud chceme nějak geometricky pracovat se zeměpisnými daty, hodí se
nejprve souřadnice bodů převést do nějakého pravoúhlého souřadného systému.
Nejznámějším takovým je UTM.
UTM rozděluje zemský povrch na tzv. zóny – oblasti dost malé na to, aby
se na nich neprojevovalo zakřivení povrchu a mohli jsme je pro praktické
účely považovat za rovinu.
V každé zóně je pak zavedena pravoúhlá souřadná síť v metrech (tedy každý bod
má x-ovou a y-ovou souřadnici udávající vzdálenost v metrech od nějakého
referenčního bodu ve východozápadním, resp. severojižním směru). A poštěstilo
se nám, že téměř celé Česko je v jedné UTM zóně (33U), takže ani nemusíme řešit
nepříjemné přechody mezi zónami. Prostě převedeme zeměpisné souřadnice do UTM a
s UTM souřadnicemi můžeme zacházet jako se souřadnicemi bodů v rovině. Můžeme
pak spočítat jejich manhattanskou vzdálenost prostým sečtením rozdílů x-ových
a y-ových souřadnic, případně jejich vzdálenost vzdušnou čarou pomocí
Pythagorovy věty.
Převod zeměpisných souřadnic do UTM je celkem komplikovaný, ale existují
různé knihovny, které se o něj postarají. Nejznámější z nich je asi pyproj,
kterou můžete nainstalovat pomocí správce balíčků pip.
Pak ji můžete použít třeba následovně:
from pyproj import CRS, Transformer
utm = CRS.from_epsg(32633)
wgs = CRS.from_epsg(4326)
na_utm=Transformer.from_crs(wgs,utm).transform
# Nyní můžete zavolat na_utm(sirka, delka)
# a dostanete dvojici utm souradnic
def manhattan(sirka1, delka1, sirka2, delka2):
x1, y1 = na_utm(sirka1, delka1)
x2, y2 = na_utm(sirka2, delka2)
return abs(x1-x2) + abs(y1-y2)
Vysvětlení tohoto kódu by bylo nad rámec seriálu, berte jej jako zaklínadlo.
Pěší přesuny a stavový prostor
Když už máme naplánované, mezi kterými dvojicemi stanovišť chceme povolit pěší
přesuny, potřebovali bychom je nějak začlenit do našeho stavového grafu.
Problém je, že jedna hrana dokáže popsat pouze přesun v jeden konkrétní okamžik.
Tedy když přidáme hranu z vrcholu (A,t, -) do vrcholu (B,t+τ,-)
(kde τ je doba potřebná na přesun), umožníme pěší přesun ze zastávky
A na B pouze v čase t a nikdy jindy. Teoreticky pěšky můžeme chodit kdykoliv,
takže bychom museli u každé zastávky mít vrcholy pro všechny možné časy a graf
by byl neprakticky velký.
Ale snadno si pomůžeme jednoduchým omezením: pěší přesuny provádíme vždy hned
po výstupu z vozidla (a čekáme až na cílové zastávce). To nalezené trasy příliš
nezmění a graf to dost zjednoduší. Nyní stačí jen projít všechny vrcholy
odpovídající příjezdu vozidla na zastávku a pro každý z nich přidat hrany
pro všechny možné pěší přesuny z této zastávky v tomto čase (předpokládáme,
že délka přesunu je omezená, takže jich nebude mnoho).
Připravili jsme se tím o možnost udělat pěší přesun na úplném začátku trasy
(pokud zrovna v tu dobu na výchozí zastávku nic nepřijíždí), kterou
by možná bylo vhodné v prohledávacím algoritmu nějak kompenzovat. Zrovna tak
jsme se připravili o možnost navázat dva pěší přesuny za sebe a obecně popisovat
pěší přesuny na delší vzdálenosti, ale to v našem modelu z principu moc nejde
(kdybychom to povolili, různou kombinací pěších přesunů se na každou zastávku
dostaneme téměř v libovolném čase, což by opět vedlo k explozivnímu nárůstu
počtu vrcholů na zastávku). Pokud bychom chtěli kombinovat delší pěší cesty
(případně třeba cesty na kole) s cestami MHD, to už je dost jiná úloha, které
se říká multimodální plánování a je o dost těžší.
Podobným způsobem můžeme vyřešit i přesuny uvnitř stanic podle pathways.txt,
ale tam asi potřebujeme umožnit několik přesunů navazujících na sebe (např.
z povrchu do vestibulu a z vestibulu na nástupiště).
Další rozšíření stavového prostoru
Koncept stavového prostoru je celkem flexibilní a snadno ho rozšíříte
o reprezentaci dalších faktů. Například v Praze lidé při nastupování do metra
obvykle přemýšlí o tom, na kterou stranu soupravy se postavit, aby v cílové
stanici byli co nejblíže výstupu (případně pokud má stanice více výstupů, tomu,
který chtějí použít).
I toto lze v našem modelu snadno reprezentovat. Stačí do vrcholů
představujících cestu ve spoji metra zakódovat informaci o tom, ve které části
soupravy se nacházíme (pro jednoduchost stačí rozlišit přední, prostřední a
zadní). Poté i vrchol představující nástupiště rozdělíme na několik částí,
mezi kterými povedou hrany ohodnocené dobou potřebnou pro přejití z jedné
části nástupiště do jiné (podobně jako u jiných hran pro pěší přesuny si musíme
rozmyslet, v jaké časy je přidat, aby jich nebylo moc).
V takto upraveném grafu pokud se vyplatí před příjezdem soupravy metra přesunout
na opačný konec nástupiště, takovouto trasu při prohledávání zcela přirozeně
najdeme.
Výpočty nad stavovým prostorem
Všechny popsané varianty stavového prostoru tvoří acyklický orientovaný graf
(DAG – directed acyclic graph), protože hrany vždy vedou z vrcholu s nižším
časem do vrcholu s vyšším časem (případně stejným, ale pokud to uděláte
rozumně, mezi vrcholy se stejným časem cyklus taky nevznikne).
DAGy jsou jednou z nejpříjemnějších tříd grafů a spousta věcí se nad nimi nechá
spočítat velmi jednoduše v lineárním čase. Jejich nejdůležitější vlastností je, že
mají topologické uspořádání (o kterém píšeme v naší grafové kuchařce)
– tedy pořadí vrcholů takové, že hrany v něm vedou jen zleva doprava.
To nám umožňuje použít techniku zvanou indukce podle topologického uspořádání.
Často chceme pro všechny vrcholy spočítat nějakou hodnotu (například délku nejkratší
cesty z nějakého pevného startovního vrcholu), přičemž umíme pro libovolný vrchol
spočítat tuto hodnotu z hodnot jeho předchůdců (vrcholů, ze kterých do něj vede
hrana).
Pak si všimneme, že pokud budeme hodnoty postupně počítat v pořadí podle topologického
uspořádání, vždy, když narazíme na nějaký vrchol, máme hodnoty pro všechny jeho
předchůdce (přímé i nepřímé) už spočítané z předchozích kroků. Často ani nemusíme
nejdřív hledat topologické uspořádání a pak podle něj procházet vrcholy – konstrukci
topologického uspořádání společně s induktivním výpočtem zvládneme jedním upraveným
prohledáním do hloubky (DFS).
Další algoritmy
Existují i jiné algoritmy speciálně navržené na hledání spojení v jízdních řádech, které
nepotřebují reprezentací pomocí DAGu. Pro příklad zmíníme algoritmus
Raptor,
který pracuje po linkách, nikoli po spojích, takže ve většině praktických případů
je rychlejší. Ale oproti velmi obecnému přístupu pomocí stavového prostoru nejde
tak snadno rozšířit na další aplikace. Jeho popis je nad rámec tohoto seriálu.
Obecně o úlohách
Pro úlohy jsou určené primárně dvě datové sady, které naleznete ve formátu GTFS
na stránce seriálu: Pražská
integrovaná doprava a české vlaky. Prosím používejte verzi z našich stránek, ať mají
všichni stejná data. Samozřejmě budeme rádi, když si vyzkoušíte i jiné datové sady
a formáty, iniciativě se meze nekladou.
Podobně jako v předchozích sériích, řešení odevzdávejte ve formě ZIP archivu, který
obsahuje:
- Krátký slovní popis, jakým způsobem jste přistupovali ke které úloze a třeba jak
vám to přišlo těžké (jako prostý text nebo PDF). Popis by měl obsahovat nějaké zamyšlení
nad časovou náročností – formou asymptotické časové složitosti (pokud ji lze
v daném případě smysluplně určit) a/nebo naměřené časové náročností na vašem počítači
pro různá data. Dále by měl obsahovat stručný popis toho, jak se váš program spouští,
jestli má nějaké parametry, případně jakým způsobem mu předat vstup (klidně editací
konstant ve zdrojáku) a v jaké podobě. Pokud váš program používá nějaké dodatečné
datové sady z jiných zdrojů či méně obvyklé externí knihovny, upozorněte na to včetně
odkazu, kde je získat, případně s jakou verzí jste to zkoušeli.
- Výstup, který požaduje zadání dané úlohy, pro každou datovou sadu uvedenou v zadání
úlohy. Budeme samozřejmě rádi, pokud se s námi podělíte i o další zajímavé výstupy.
- Zdrojový kód programu, který jste použili pro řešení. Pokud jste zkoušeli více programů
či jejich variant, případně použili různé programy pro různá data, zahrňte všechny.
Vaše programy by měly zvládat načíst jízdní řády ve formátu GTFS (v rozbalené
podobě, tedy jako adresář s CSV soubory). Podpora jiných formátů je volitelná.
Stačí, když ho otestujete na datových sadách uvedených v zadání, ale měl by být
psán tak, aby se dalo rozumně čekat, že si do nějaké míry poradí i s jinými.
Abychom měli podobné výstupy, sjednoťme si alespoň trochu přestupní podmínky.
Uvažujte minimální dobu na přestup v rámci jednoho stanoviště 2 minuty (zahrnuje
i rezervu na zpoždění přijíždějícího spoje). Pro pěší přesuny, pokud budete
odhadovat čas na základě vzdálenosti, předpokládejte rychlost 1 m/s (3.6 km/h,
zahrnuje nějakou rezervu na přecházení ulic a další zdržení). Tedy pro dvě stanoviště
vzdálená 60 metrů uvažujte minutu na přesun plus dvě minuty pevnou časovou rezervu,
tedy celkem minimálně tři minuty mezi příjezdem jednoho spoje a odjezdem navazujícího.
Pro odhad vzdálenosti použijte primárně manhattanskou vzdálenost s maximální
přestupní vzdáleností 450 metrů. Sofistikovanějším řešením, která například
nějak využívají mapová data, se rozhodně nebráníme (a možná si vyslouží i
nějaké bonusové body), v takovém případě zkuste trefit parametry, které dávají
řádově podobné výsledky.
Pokud se chcete geografickým datům úplně vyhnout, můžete uvažovat pevnou přestupní
dobu mezi dvěma zastávkami v rámci uzlu 5 minut (v rámci jednoho stanoviště stále
jen dvě minuty), byť možná za trochu méně bodů.
V případě metra uvažujte penalizaci 3.5 minuty za přesun mezi výstupem na povrchu
a nástupištěm. Můžete to zkusit zpřesnit použitím časů z pathways.txt,
případně třeba odhadnout na základě hloubky stanice pod povrchem (dá se snadno
najít), řekněme 5 s na metr hloubky.
V případě dat, která nerozlišují stanoviště (např. vlaky) uvažujte pevný čas na
přestup 10 minut. Kdybyste si chtěli hrát, ještě lepší
varianta je uvážit různé časy podle toho, z jakého typu vlaku na jaký
přestupujete. Například z rychlíku na osobní vlak potřebujete menší časovou
rezervu (protože osobní vlak obvykle počká déle v případě zpoždění), opačným
směrem větší. Též by bylo dobré zohlednit, že u některých vlaků je poznámka
„vlak nečeká na žádné přípoje“. Vyžadovalo by to trochu upravit konstrukci
grafu (protože najednou záleží na tom, jakým spojem dál pojedete), zkuste si
rozmyslet jak.
U vlaků nemusíte uvažovat obecné pěší přesuny (byť můžete), ale bylo by dobré
přinejmenším ručně přidat ty nejvýznamnější, alespoň Praha hl.n. – Praha
Masarykovo n. (řekněme 15 minut).
Zadání úloh
Úkol 1 [5b]
Rádi bychom našli jakési „dopravní centrum“ – tedy zastávku,
ze které se co nejsnáze dostaneme do libovolné jiné.
Jak to definovat formálně? Na vstupu dostanete datum a rozsah možných časů
odjezdu (třeba 8:00–9:00). Korektní
spojení z uzlu x do uzlu y definujeme jako spojení z libovolného stanoviště
uzlu x do libovolného stanoviště uzlu y, které z výchozího stanoviště
vyjíždí v zadaném časovém intervalu.
Dojezdový čas z uzlu x do y je nejmenší jízdní doba (rozdíl mezi časem odjezdu
z x a časem příjezdu do y) nějakého korektního spojení. Pokud spojení začíná nebo
končí cestou metrem, musíme připočítat čas potřebný k cestě z povrchu / na povrch.
Excentricita nějakého uzlu x je maximum z dojezdových časů z x do všech
ostatních uzlů. Centrum je pak uzel s nejmenší excentricitou.
Vaším úkolem je napsat program, který dostane na vstupu jízdní řád, datum a rozsah časů odjezdu
odjezdu a nalezne centrum. Pokud k tomu lze váš algoritmus jednoduše upravit,
vypište třeba 10 uzlů s nejmenší excentricitou – ale stačí i jeden.
Vyzkoušejte na datových sadách PID i vlaků. Odjezd uvažujte v pondělí v 8:00–9:00.
Ve svém řešení uveďte nalezené centrum spolu s jeho excentricitou.
Než začnete, zkuste si tipnout, jak to dopadne.
Úkol 2 [5b]
V prvním dílu seriálu byla řeč o heatmapách jakožto
užitečném způsobu vizualizace geografických dat. V této sérii si taky jednu
heatmapu nakreslíte – konkrétně heatmapu dojezdových časů. Na vstupu dostanete
jízdní řád, identifikátor výchozího uzlu a datum a povolený rozsah časů odjezdu.
Pro každý uzel nakreslete
do mapy barevné kolečko, jehož barva odpovídá dojezdovému času (dle definice
z předchozího úkolu) z výchozího uzlu do tohoto uzlu.
Dále přidejte druhý režim použití, kdy na vstupu budou dva výchozí uzly a
nakreslíte heatmapu rozdílů v dojezdových časech z jednoho a z druhého. Použijte
jednu barevnou škálu pro kladné rozdíly – kdy z prvního výchozího uzlu se na
dané místo dostanete rychleji než z druhého – a jinou pro záporné.
Pošlete nám obrázky z následujících výchozích stanic pro PID:
- I. P. Pavlova
- Malostranské náměstí
- rozdílový mezi nimi
a z následujících stanic pro vlaky:
- Praha hl.n. + Praha Masarykovo n. (uvažujte odjezdy z obou, jako by to byla jedna stanice)
- Brno hl.n.
- rozdílový mezi nimi
Ve všech případech uvažujte odjezd v pondělí v 8:00–9:00.
Úkol 3 [5b]
Najděte trasu v síti PID, která za 24 hodin (od půlnoci z neděle na pondělí
do půlnoci z pondělí na úterý) projede co nejvíc různých linek. Dvě linky
považujeme za různé, pokud mají různé route_short_name. Můžete používat
všechny linky včetně vlakových, příměstských, atd.
Efektivní přesné řešení pravděpodobně neexistuje; můžete použít libovolné
aproximace či heuristiky. Hlavním kritériem bodového ohodnocení bude, kolik
linek zvládne vaše řešení projet.
Jako výstup odevzdejte itinerář trasy v podobě textového souboru, kde každý řádek
popisuje cestu jedním spojem (v pořadí, v jakém je použijete). Na jednom řádku
budou následující položky oddělené mezerou:
- identifikátor spoje (
trip_id)
- v jaké zastávce do spoje nastoupíme (
stop_sequence v rámci daného spoje)
- v jaké zastávce ze spoje vystoupíme (též
stop_sequence v rámci daného spoje)
Filip Štědronský
Řešení
 32-3-1 Zkrat (12 bodů)
32-3-1 Zkrat (12 bodů) Systémy hvězdné lodě Hefaistos jsou ochromené, protože část obvodů byla vyzkratována.
Hlavní inženýr potřebuje nahodit počítačové jádro, ale to nelze,
dokud existuje spojení počítačového jádra a místa zkratu.
Systémy hvězdné lodě Hefaistos jsou ochromené, protože část obvodů byla vyzkratována.
Hlavní inženýr potřebuje nahodit počítačové jádro, ale to nelze,
dokud existuje spojení počítačového jádra a místa zkratu.
 32-3-2 Hledání konstelace (12 bodů)
32-3-2 Hledání konstelace (12 bodů) Lehčí varianta (za 7 bodů): Vyřešte úlohu jenom ve 2D, tedy namísto kvádrů uvažujte pouze
obdélníky o rozměru
Lehčí varianta (za 7 bodů): Vyřešte úlohu jenom ve 2D, tedy namísto kvádrů uvažujte pouze
obdélníky o rozměru 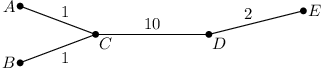
 32-3-6 Jízdní řády (15 bodů)
32-3-6 Jízdní řády (15 bodů)