Čtvrtá série osmého ročníku KSP
Řešení úloh
- 8-4-1: Cesta tam a zase zpátky
- 8-4-2: Ďábelské mocniny
- 8-4-3: Top secret
- 8-4-4: Penězokazi
- 8-4-5: (Ne)konečné automaty
8-4-1 Cesta tam a zase zpátky (Zadání)
Překvapilo nás, že tuto úlohu nikdo nevyřešil správně. Přitom její obtížnost je s ostatními úlohami srovnatelná. Je to asi tím, že to není žádný zprofanovaný evergreen.
Každému, kdo se trochu vyzná v teorii grafů, muselo být jasné, že jde o minimální zesilněsouvislení orientovaného grafu.
Nadefinujme si nejdříve nějaké pojmy v duchu zadání:
Okres (jinak též silně souvislá komponenta) je maximální množina měst, ve které je možné se dostat z každého města do každého. Vstupní okres je okres, do kterého nevedou žádné silnice. Výstupní okres je okres, ze kterého nevedou žádné silnice (jistě existuji i vstupně-výstupní okresy).
Je zřejmé, že hledaný algoritmus musí do každého vstupního okresu zavést alespoň jednu silnici a zároveň z každého výstupního okresu vyvést alespoň jednu silnici. To znamená, že musí přídat minimálně tolik, kolik činí maximum z počtu vstupních a výstupních okresů – tyto počty totiž nemusí být stejné.
Algoritmus, který přidává právě tento minimální počet silnic, tedy najde vždy optimální řešení. Tuto vlastnost splňuje např. algoritmus následující:
1. Dokud existují vstupní okres A a výstupní okres B takové, že z okresu A nevede cesta do okresu B, zaveď silnici z okresu B do okresu A (resp. z libovolného města okresu B do libovolného města okresu B).
V tomto kroku se určitě nezmění počet okresů ve státě – ke snižení počtu okresů může dojít pouze, když se mezi nějakými vytvoří cyklus, což je vzhledem k podmínce nemožné; zvýšení počtu okresů přidáním silnice taktéž není možné. S každou přidanou silnicí ubyde právě jeden vstupní a právě jeden výstupní okres. Nové vstupní resp. výstupní okresy se nevytvoří.
2. Dokud existuje vstupní okres A a od něj různý výstupní okres B, zaveď silnici z okresu B do okresu A.
V tomto kroku se přidáním každé silnici spojí nějaké okresy v jeden. Zároveň ubyde právě jeden vstupní a právě jeden výstupní okres. Nový vstupní resp. výstupní okres vznikne pouze tehdy, když před přidáním hrany existoval právě jeden vstupní resp. výstupní okres – vyplývá z podmínky v prvním kroku algoritmu.
Po ukončení druhého kroku algoritmu exituje pouze jeden vstupně výstupní okres – tedy je možné se dostat z každého města do každého.
Algoritmus hledá minimální řešení. Důkaz je zřejmý z uvedeného komentáře.
Program si zadané silnice ukládá do matice sousednosti. Z této matice pak klasickým algoritmem spočte matici dostupnosti (tranzitivní uzávěr) o složitosti O(N3 log N).
V této matici pak hledá silnice, které je nutné přidat, podle výše uvedených pravidel. Po každém přidání silnice patřičně opraví matici dostupnosti. Vzhledem k tomu, že silnic nikdy nebude přidáno více jak N, je složitost implementace každého z kroků algoritmu O(N3).
Časová složitost implementace je tedy: O(N3 log N). Použitím vhodnějších datových struktur je možné časovou složitost snížit, paměťové nároky jsou O(N2). Algoritmus je zřejmě konečný.
8-4-2 Ďábelské mocniny (Zadání)
Tato úloha posloužila jako dokonalý "chyták" – polovina z vás použila rozkladu na prvočinitele (nejspíše se inspirovala úlohou následující), který ovšem má k optimálnímu řešení velice daleko. Jeden protipříklad za všechny: počítáme a220. Rozklad na prvočinitele nám dá stejný počet násobení (1048575), jako kdybychom počítali přímo, zatímco zvolím-li a0=a, ai+1 = ai ·ai, pak a20 bude kýžený výsledek za pomoci pouhých 20 násobení.
Základním trikem je tedy (ne, pravda, k dosažení opravdu optimálního počtu násobení – to je netriviální, ale asymptoticky optimálního ano) rozklad exponentu do dvojkové soustavy (tedy jako b = 2a0 + ...+ 2ak, kde k ≤ log2 b), čímž dostaneme ab = a2a0 ·… ·a2ak, přičemž všechna a2ai dokážeme postupným umocňováním na druhou spočítat v čase O(log N) a poté je v témže čase vynásobit, tedy celkově O(log N).
Největší číslo dosažitelné k násobeními je jistě a2k (důkaz nechť si laskavý čtenář provede sám), tudíž alespoň pro čísla tohoto tvaru není lepší řešení než logaritmické, pročež asymptoticky to lépe než logaritmicky nejde.
Úloha by si možná zasluhovala o trošku lepší důkaz, nicméně by tím celková velikost všech vzorových řešení vzrostla nad únosnou mez, takže případné další dotazy zodpovím osobně.
8-4-3 Top secret (Zadání)
Uvedený příklad je speciálním případem velmi praktické úlohy, na kterou ale neexistuje opravdu rychlé řešení: rozkladu na prvočinitele. Toho se hojně využívá v šifrování – mnoho šifrovacích algoritmů je založených na tom, že rozložit na prvočinitele opravdu velké číslo je v rozumném čase nemožné. Dokonce se pořádají soutěže (RSA factoring challenge a jiné) v rozkladu čísel – firmy zabývající se šifrováním zajímá, která čísla je možno rozložit a která ne.
Pro zajímavost uvádím, že s pravděpodobností kolem 20% je možné rozložit náhodně zvolené 250-ti místné číslo.
Vhodnou metodou pro daný příklad je "triviální dělení" – pro všechna čísla i ∈{2, … , √N} zkusíme spočítat N mod i a vyjde-li 0, máme řešení. Vzhledem k zadání (číslo je součinem dvou prvočísel) lze druhé prvočíslo dostat jako n/i a není nutné zjišťovat, jestli není i ≤ √N. Dále není nutné testovat prvočíselnost čehokoliv – pokud jdeme od dvojky nahoru, tak první číslo, které bude dělit N bude určitě prvočíslo. Popsaný algoritmus má časovou složitost O(√N). Jistého zlepšení (ovšem pouze konstanta krát) lze dosáhnout tím, že se na začátku zjistí, jestli N není dělitelné 2-mi nebo 3-mi (v případě, že ano, je výsledek jasný), a v případě že ne, testovat jen čísla tvaru 6k-1 a 6k+1.
Poměrně častou chybou byly různé pokusy o dělení pouze prvočísly. Takový algoritmus měl typicky složitost kolem O((√N)2) ≈ O(N), t.j. výrazně pomalejší než jednoduché řešení.
8-4-4 Penězokazi (Zadání)
Tuto úlohu všichni řešitelé nějak vyřešili. Potíž bylo v tom "nějak". Záleželo totiž na tom, jak jste pochopili zadání úlohy. My jsme dle zadání považovali přístup k vnější paměti za daleko pomalejší, než je přístup k hlavní paměti, které však bylo pouze 4 kB=4096 B = 32768 bitů. Data bankovek byla také uložena ve vnější paměti, kdo by se přeci namáhal psát skoro 100000 čísel.
Obecně existují dvě možmosti, jak si zapamatovat číslo – mít ho uložené v datové části, nebo si ho pamatovat pomocí stavu programu (ti, co pochopili teorii automatů z příkladu na pokračování, vědí, o co jde). Druhou možnost nevyužil nikdo, tak se jí zabývat nebudu. Avšak pokud by někdo chtěl opravdu rychlý program, tak by se toho dalo využít i za cenu daleko většího programu.
Většina z vás úlohu řešila z jiného pohledu, totiž aby onen
program běžel na vašem počítači pod vaším systémem rychle. Chtěli jsme
jako vždy řešení nezávislé na systému. Podle toho také řešení mělo
vypadat. Bohužel spousta z vás používala speciální operace
blockread/write, které nejsou na jiných systémech definovány. Naše řešení
se o to opírat nemůže – nevíme nic o tom, jak ona vnější paměť vypadá, a
pokud je to disk, tak jaká je jeho struktura – ta vypadá podle toho jak ji
připravil operační systém. Tedy již chapete, že nelze považovat
blockread stovky čísel za jeden přístup k vnější paměti, nýbrž za 100 přístupů.
Pokud toto vezmeme v úvahu, tak bychom si správné řešení představovali
takto:
Na vstupu máme velké množství čísel (okolo 100000) typu longint.
Definujeme si pole bitů o velikosti 32400, tj. 4050 bytů, zbytek ponecháme na
proměnné. Jednou přečteme celý vstup a jsme schopni říci, zda se v
intervalu 1..32400 něco opakuje, neboť pro každé číslo z tohoto intervalu si
budeme pamatovat, zda jsme ho už četli, nastavením bitu v poli s pořadím
hodnoty onoho čísla. Např. pro číslo 127 nastavíme 127. bit. Poté
pořebujeme ještě otestovat soubory na disku, které jsme vytvořili. Pro
každý soubor (jsou celkem nejvýše 4), existuje-li, vymažeme celé bitové
pole, načítáme čísla a opět přitom nastavujeme bity v poli jako v prvním
případě.
Složitost algoritmu: Je zřejmé, že je lineární, nás však zajímá počet přístupů na vnější paměť (disk), které program nejvíce zpomalují. Nejprve čteme 4N bytů (N longintů), přičemž přibližně 2/3·N čísel typu integer opět zapisujeme, načež je čteme zpět. Celkem tedy přeneseme mezi diskem a vnitřní pamětí přibližně 7N bytů.
Poznámka k programu pro neznalé bitových operací: shr je rotace bitů
doprava – např: A shr 2 vydělí celé kladné číslo čtyřmi. Podobně
A shl 1 násobí dvěma. Je to daleko rychlejší než dělení či násobení.
A and 15 je bitový součin, což je totéž, jako A mod 16,
ale opět rychlejší, neboť se neprovádí žádné dělení.
8-4-5 (Ne)konečné automaty (Zadání)
Došlých řešení této úlohy nebylo mnoho a ne všechna byla správně. Mnozí z Vás se pustili pouze do části a, tj. do sestrojení předepsaného automatu. Část b, tj. napsání generátoru konečných automatů, řešilo pouze asi 15 řešitelů, ideální řešení však k naší lítosti nenalezl nikdo, ač mnozí byli blízko.
Nejvíce problémů s částí a bylo v pochopení, jaký jazyk se má rozpoznávat. Zadání říkalo něco takového:
- L1 = { w∈{a, b}* ; w obsahuje podslovo bbba }
- L2 = { w∈{a, b}* ; w obsahuje podslovo baaa }
- L3 = { w=xy ; x∈L1 a zároveň y∈L2 }
což znamená tolik, že slova z jazyka L3 se mají dát rozdělit na dvě nepřekrývající se části, a to tak, že první část bude z prvního jazyka, tedy bude obsahovat slovo bbba, a druhá bude z druhého jazyka, tedy bude obsahovat slovo abbb.
"No problem," řekl nejspíše každý, kdo správně pochopil zadaní, sedl a automat napsal.
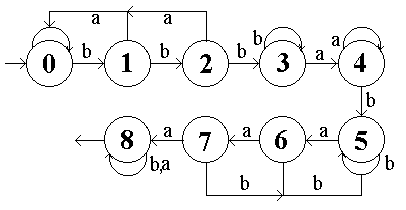
Ani my nemáme v podstatě k automatu co dodat, a tudíž Vám jej rovnou předkládáme:
| KA | = (Σ, Q, δ, D0, F ) |
| Σ | = { a, b} |
| Q | = { D0, D1, D2, D3, D4, D5, D6, D7, D8 } |
| F | = { D8 } |
| δ(D0, a)=D0 | δ(D0, b)=D1 |
| δ(D1, a)=D0 | δ(D1, b)=D2 |
| δ(D2, a)=D0 | δ(D2, b)=D3 |
| δ(D3, a)=D4 | δ(D3, b)=D3 |
| δ(D4, a)=D4 | δ(D4, b)=D5 |
| δ(D5, a)=D6 | δ(D5, b)=D5 |
| δ(D6, a)=D7 | δ(D6, b)=D5 |
| δ(D7, a)=D8 | δ(D7, b)=D5 |
| δ(D8, a)=D8 | δ(D8, b)=D8 |
Část b byla o poznání těžší, než část předešlá, a proto ji také málokdo řešil a vyřešil.
Nejlepší došlá řešení pracovala v čase O(N2), kde n je délka hledaného slova. Tato řešení obvykle získala plný počet bodů, ostatní řešení, pokud vůbec fungovala, dostala méně.
Správný algoritmus se dal vytvořit ve dvou krocích. V prvním dosáhneme časové složitosti O(A·N), kde A je velikost abecedy, a ve druhém pak toto řešení drobnou úpravou převedeme na řešení s lineární časovou složitostí O(N). Lepšího času lze jistě těžko dosáhnout (minimálně musíme to slovo projít, abychom věděli, pro co generujeme automat).
Základní otázkou, kterou si každý řešitel musel položit a obvykle si na ni i odpovědět, bylo, jak vůbec může náš hledaný automat vypadat.
Správná odpověď na tuto otázku byla ta, že bude mít n+1 stavů. Každý stav bude mít přiřazeno jméno, které odpovídá nějaké počáteční části hledaného slova, a to tak, že i-tému stavu bude odpovídat prvních i znaků hledaného slova. Nultému stavu samozřejmě odpovídá prázdný řetězec a poslednímu stavu celé hledané slovo.
Od automatu pak budeme požadovat to, aby v průběhu jeho výpočtu nad vstupním textem označení stavu, ve kterém se nachází, odpovídalo tomu, co zatím přečetl, přesněji – zakončení zatím přečteného kusu vstupního textu.
Například pro hledaní slova "ksp" budeme mít automat se čtyřmi stavy: `', `k', `ks', `ksp', který se po přečtení úseku textu "ošklivý ks" bude nacházet ve stavu `ks'.
Dalším požadavkem na tento automat bude to, že pokud se automat může nacházet ve více stavech, pak se bude nacházet ve stavu s delším názvem (srovnej stavy `šošo'a `šo' pro slovo "šošolka" po přečtení "občané byli šo" a "pták měl velkou šošo".) Splnění této podmínky nám zajistí jednu podstatnou vlastnost automatu – v okamžiku, kdy se na konci zatím přečteného kusu textu vyskytne hledané slovo, budeme ve stavu, který je označen tímto celým hledaným slovem a nikde jinde. Nikdy jindy se tam také dostat nemůžeme, a tedy pokud se tam dostaneme, pak jsme vyhráli, našli jsme hledané slovo a už se odsud nehneme a zbytek textu ignorujeme.
Skončí-li tedy automat výpočet v tomto posledním stavu, musel text obsahovat hledané slovo. Pokud ne, pak ani text toto slovo neobsahoval.
Zbývá už jen zodpovědět otázku, jak bude vypadat přechodová funkce nešeho automatu.
Je zřejmé, že všechny přechody z posledního stavu povedou zpět do tohoto stavu.
Dále z toho, co jsme řekli vyplývá, že nejlépe bude, pokud tuto funkci budeme pro ostatní stavy sestrojovat postupně od nultého stavu do předposledního.
Přechodová funkce z nultého stavu bude vypadat tak, že pro všechny znaky mimo jednoho bude vést zpět do tohoto nultého stavu. Vyjímku tvoří první znak hledaného slova, pro který se přesuneme do následujícího, prvního, stavu.
Je vidět, že toto splňuje naše podmínky, aby stav, ve kterém jsme, odpovídal tomu, co jsme přečetli. Pokud jsme totiž v nultém stavu, pak konec přečteného textu neodpovídá žádnému počátečnímu úseku hledaného slova, tudíž přečtením dalšího znaku se to určitě nemůže zlepšit, resp. nemůžeme se pohnout dále, než na první stav, kam se pohneme, právě když přečteme první písmenko hledaného slova.
Pro nultý stav máme tedy přechodovou funkci nalezenou. Jak ji nalezneme pro další stavy?
Pojďme generovat přechodovou funkci pro stav s označením y, přičemž pro kratší stavy ji už známe. Vezměme si stav s třeba i prázdným označením u takovým, že y = xu, pro nějaké slovo x, a u je kratší než y. Zřejmě takový stav u existuje – minimálně nultý stav s prázdným označením – a už pro něj jistě známe přechodovou funkci.
Pokud se automat dostane do stavu y, znamená to, že slovo zatím končilo na toto slovo, tedy na xu, neboli pokud odhlédneme od požadavku, že se vždy nacházíme v nejdelším možném stavu, mohli bychom být klidně ve stavu u. Všechny přechody ze stavu u by se tedy daly použít i pro stav y, s tím, že by však mohlo dojít k porušení podmínky maximální délky, čili pokud se po přečtení nějakého znaku Z ze stavu u přejde do stavu w, pak by se tam klidně mohlo přejít i z y. (w = vZ, u = cv, y = xu ⇒y = xcv ⇒ přechod z y do w neporuší podmínku o jménech stavů)
Pokud bychom si však původně ze všech možných stavů u vybrali ten s nejdelším označením, pak ve všech případech, kromě přechodu pro další znak hledaného slova, který se musí nastavit zvlášť (viz. dále), k porušení podmínky maximálnosti nedojde. To z toho důvodu, že přechody ze stavu u jsou již pro stav u maximální. Pokud by se totiž pro nějaký znak Z' mělo přejít ze stavu y do nějakého stavu w' kratšího než je y, pak to znamená, že w' = v' Z' a y = pv', pro nějaká v' a p. Ovšem to speciálně znamená, že v' je také stav našeho automatu kratší než y, který je taktéž jeho zakončením, ale z výběru u, jakožto maximálního stavu zakončujícího y vyplývá, že v' Z' musí být i přechod pro u, protože v' musí být též zakončením u.
Nakonec nadefinujeme přechodovou funkci pro stav y a pro znak, kterým pokračuje hledané slovo, jako přechod do stavu s o jedna delším označením než y.
Shrnutí: přechodová funkce pro stav y je stejná jako funkce pro nejdelší stav zakončující y s tou výjimkou, že pro další znak je rovna dalšímu stavu za y.
Z toho okamžitě vyplývá náš algoritmus.
Zbývá pouze zodpovědět otázku, jak rychle nalézt pro stav y nejdelší jeho zakončení. Odpověď je nasnadě. Do stavu y jsme přešli ze stavu y' přes nejaký znak. Hledaný stav u je stav, kam by přešlo y', kdyby nemuselo přejít do y, což je stav, kam by vedla přechodová funkce, kdyby se při hledání přechodové funkce pro y' nepoužilo na závěr pravidlo o výjimce pro pokračovací znak. Stačí si tedy potřebnou informaci zjištěnou při generování přechodové fce pro y' zapamatovat pro dobu generování funkce pro y.
Tento algoritmus bude mít časovou složitost O(A·N), protože pro každý stav musíme opsat přechodovou funkci nějakého předchozího stavu a změnit ji v jednom bodě, tedy n-krát provedeme opsání, které trvá O(A).
Tento algoritmus se dá ještě zlepšit na časovou složitost O(n), když si všimneme, že většina přechodů jde zpět do nultého stavu `'. Pro každý stav si tedy bude stačit pamatovat pouze ty přechody, které nevedou zpět do nultého stavu. Těchto přechodů je maximálně 2N, včetně těch do následujícího stavu. Jelikož časová složitost našeho algoritmu spočívala v kopírování přechodové funkce, tak ježto nyní kopírujeme maximálně 2N položek, máme časovou složitost O(n).
Důkaz toho, že je maximálně 2N netriviálních přechodů zde nebudeme uvádět. Vyplývá to z činnosti jiného možného algoritmu, řešícího naši úložku, jehož časová složitost sice je O(N2), ale nalezne pouze těchto 2N netriviálních přechodů.
Paměťová složitost našeho algoritmu je pro pomalejší verzi O(A·N) a pro rychlejší O(N).
Autorské programy pro obě verze algoritmu jsou uvedeny. V poli
ekviv je pro každý stav uloženo číslo nejdelšího menšího stavu,
který je jeho zakončením. (Toto pole není ve skutečnosti
potřeba, protože čteme vždy poslední zapsanou položku a místo
něj by stačila jedna proměnná, je zde však z didaktických
důvodů.)
V poli delta je uložena přechodová funkce hledaného automatu.
V první verzi programu je tam uložena vždy celá, ve druhé pak
pouze její netriviální část.
Více již komentáře přímo v programech.