Druhá série třicátého pátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám druhé číslo hlavní kategorie 35. ročníku KSP.

Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Také na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál na lineární algebru.

Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.

Odměny & na Matfyz bez přijímaček

• Termín série: 18. prosince 2022 ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Sladkou odměnu si vyslouží ten, kdo získá z této série alespoň 42 bodů.

Zadání úloh

• 35-2-1: Kde je Dan?
• 35-2-2: Zápisky z přednášky
• 35-2-3: Hroší šanta
• 35-2-4: Kamínky
• 35-2-S: Lineární zobrazení
• 35-2-X1: Oblázky

35-2-1 Kde je Dan? (11 bodů)

Na soustředění KSP se hrála seznamovací hra, při které stálo několik účastníků a organizátorů v kroužku. Ten, kdo byl na řadě, se podíval na lidi na druhé straně kroužku a řekl jejich jména. Už si bohužel nikdo nepamatuje, kde kdo z účastníků stál, ale víme, na kterých pozicích stál někdo z organizátorů. Zároveň si také pamatujeme, kolik organizátorů pojmenoval Dan, když byl na řadě. Zajímalo by nás, kde všude mohl Dan stát, když předpokládáme, že pojmenoval všechny lidi správně.

V kroužku stálo N lidí a M z nich bylo organizátorů. Pozice v kroužku jsou očíslovány po směru hodinových ručiček čísly 1 až N tak, že pozice i a i+1 jsou vedle sebe, a zároveň pozice 1 je vedle pozice N. Člověk na tahu vždy pojmenovával K lidí, kteří stáli přímo proti němu.

Slibujeme, že:

• M<N – organizátoři tvoří výraznou menšinu ze všech lidí
• N bude vždy sudé
• K bude vždy liché
• a také K < N

Tedy lidé naproti Danovi jsou vždy jednoznačně určeni – je to ten přímo naproti Danovi (tedy takový člověk, že jejich pozice se liší právě o N/2) a dále (K - 1)/2 lidí napravo i nalevo od tohoto člověka.

Víme, že mezi těmi K lidmi, kteří stáli naproti Danovi, bylo X organizátorů.

Na kolika možných pozicích mohl Dan stát? Už si ani nepamatujeme, jestli jsme Dana počítali mezi organizátory nebo ne, takže berte v potaz obě možnosti.

Počet lidí v kroužku (a tedy i výsledných možností) může být opravdu velký, a proto bude v některých jazycích zapotřebí použít 64-bitového datového typu (v C++ je to long long int). Pokud programujete v Pythonu, pak toto řešit nemusíte.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku jsou čísla N, M, K a X oddělená mezerou. Na druhém řádku následuje M čísel popisujících, na kterých pozicích stáli organizátoři. Indexujeme od jedné.

Formát výstupu: Jediné číslo, a to počet pozic, na kterých mohl Dan stát, aby naproti němu bylo X organizátorů.

6 3 3 2
2 6 3

3

Řešení

35-2-2 Zápisky z přednášky (12 bodů)

Jirka jel přednášet na Krutou Smršť Přednášek (jste také zváni!). Povídal o datové struktuře jménem binární halda (mezi přáteli občas jen halda). Ta reprezentuje nějakou množinu čísel a umožňuje nám vkládat do ní nové číslo, ptát se na nejmenší číslo v ní a následně ho odebrat.

Haldu si můžeme přestavit jako zakořeněný strom. V každém vrcholu je uložené jedno číslo, přičemž platí, že je vždy menší nebo stejně velké než čísla v jeho potomcích. Jedná se o binární vyvážený strom, tedy všechny vrcholy mají nejvýše dva potomky, a ti, co mají méně než dva, leží v nejhlubší nebo druhé nejhlubší hladině.

Haldu můžeme snadno reprezentovat pomocí jednoho pole. Její kořen leží na indexu 1 a potomci vrcholu na indexu i leží na indexech 2i a 2i+1. Pokud jste ještě Jirkovu přednášku neabsolvovali, můžete se více o haldách dozvědět v naší kuchařce.

Dan Jirkovu přednášku poctivě absolvoval, a dokonce si z ní dělal poznámky toho, co bylo na tabuli. Má tam nakreslenou haldu, na které Jirka následně ukazoval operaci nalezení a odstranění nejmenšího čísla. Na přednášce Jirka opakoval tuto operaci několikrát po sobě a Dan si zapisoval, jaké číslo při každé operaci odebral. Ovšem nyní se Dan dívá na zápisky a nemůže přečíst K-té odebrané číslo.

Pomozte Danovi pouze za pomocí původní haldy zadané v poli zjistit, které číslo bylo odebráno jako K-té. Můžete předpokládat, že K je řádově menší než počet prvků původní haldy N. Složitost svých algoritmů tedy můžete odhadovat nejenom pomocí N, ale i K. Můžete předpokládat, že pole reprezentující haldu již máte načtené v paměti.

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

Řešení

35-2-3 Hroší šanta (10 bodů)

Kubovi se na botanické burze podařilo sehnat vzácnou šantu hroší (Nepeta hippopotamis). Traduje se, že odvar z jejích listů pomáhá zklidnit mysl a odbourává stres.

Kuba ví, že taková hroší šanta se má správně zalévat právě K litry vody. On má ale k dispozici pouze dva džbány s kapacitami A a B litrů. Pro libovolný z těchto džbánů Kuba může v jednu chvíli provést jednu z následujících akcí:

• naplnit jej až po okraj,
• celý ho vylít,
• přelít ho do druhého džbánu, dokud druhý džbán nebude plný, nebo dokud v prvním nedojde voda.

Poraďte Kubovi, jak má vodu přelévat, aby mu zbylo K litrů vody v jedné z nádob. Kuba by se ale nerad moc nadřel, proto najděte nejkratší posloupnost akcí, která tohle splňuje. Slibujeme, že taková posloupnost existuje.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku jsou dvě čísla A, B oddělená mezerou, představující kapacitu obou džbánů. Slibujeme, že A ≠ B. Na druhém řádku se nachází číslo K s cílovým objemem vody v jedné z nádob.

Formát výstupu: Na první řádek vypište počet akcí, potom vypište popis jednotlivých akcí. Každou akci vypište jako jeden ze znaků AaBb<>: A znamená naplnění prvního zadaného džbánu vodou, B je naplnění toho druhého. Znak a je pokyn k vylití prvního džbánu, b k vylití druhého. Znak > přelije první džbán do druhého a < naopak.

Výstup můžete jakoliv odřádkovávat a prokládat mezerami. (Avšak na prvním řádku vypište jen počet akcí.)

4 11
5

10
A	>A>  A

> b
>A>

Řešení

35-2-4 Kamínky (12 bodů)

Tři dobrodruhové, Bojovník Khebir, zloděj Srunvor a kouzelnice Preslana, se po porážce draka vrátili do své oblíbené hospody U Hrocha, aby doplnili síly.

Khebir uviděl v rohu tajemného poutníka v kápi, kolem kterého se shromáždila kupa vesničanů. S vesničany hrál následující hru: Tajemný poutník nejprve naskládá barevné kamínky do řady. Poté vesničan může vždy zvolit dvojici stejně barevných kamínků vedle sebe, které tajemný poutník vrátí zpátky do pytlíku. Vesničan volí dvojice, dokud buď nejsou všechny kamínky v pytlíku, v takovém případě vyhraje vesničan, nebo neexistuje dvojice sousedních kamínků se stejnou barvou, v takovém případě vyhrává poutník.

Khebir se už už chtěl vsadit a pustit do hry, jenže Preslana ho zastavila, protože si myslí, že Khebir nemůže vyhrát. Pomůžete jejich spor rozseknout?

Pro zadanou posloupnost barevných kamínků najděte algoritmus, který nám řekne, zdali vyhrát lze, nebo ne, a případně jak.

Například pro řadu kamínků červený, modrý, modrý a červený stačí nejprve vybrat dva modré vedle sebe a poté dva červené, které se k sobě nově dostanou, a hru tak vyhrát lze. Ale naopak pro řadu zelený, červený, modrý, modrý, zelený, červený sice můžeme na začátku vybrat dva modré kamínky vedle sebe, ale ani po jejich odstranění nevznikne žádná další stejně barevná dvojice vedle sebe a hru tak prohrajeme.

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

Řešení

35-2-X1 Oblázky (10 bodů)

Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.

Následující úloha navazuje na úlohu 35-2-4

Preslana obvinila tajemného poutníka z toho, že kamínky jsou rozdané tak, že vždy vyhraje tajemný poutník. Tajemný poutník se proto rozhodl, že změní pravidla – místo toho, aby se vybíraly dvojice stejně barevných sousedních kamínků, nyní lze vybrat dvojice nebo trojice stejně barevných sousedních kamínků. Preslanu by zajímalo, jestli jde hru vyhrát s novými pravidly. Pomůžete jí s tím?

Pro zadanou posloupnost barevných kamínků najděte algoritmus, který nám řekne, zdali vyhrát lze, nebo ne, a případně jak.

Řešení

35-2-S Lineární zobrazení (15 bodů)

Právě čtete druhý díl seriálu. Pokud jste neřešili ten první, pro pochopení následujících odstavců je vhodné si jej přinejmenším přečíst. Úlohy z něj je stále možné odevzdávat za polovinu bodů.

V tomto dílu se podíváme na lineární zobrazení, která nám umožní matematicky popsat transformace obrázků. Úvahy o nich nás posléze zavedou k maticím.

Všechny úlohy z tohoto seriálu odevzdávejte dohromady v jednom zazipovaném archivu. Termín odevzdání je shodný s termínem pro druhou sérii. Poté lze odevzdávat za snížený počet bodů až do konce ročníku.

Zobrazení

Budeme zkoumat transformace následujícího obrázku:

Můžeme si představit, že se obrázek skládá z mnoha bodů. Každý z těchto bodů budeme interpretovat jako vektor. Chceme-li popsat určitou transformaci obrázku, musíme říci, kam se každý z těchto vektorů má přesunout.

Zobrazení pro nás bude funkce f, která jako argument dostane vektor x v původním obrázku a převede jej na vektor f(x) v transformovaném obrázku.

Takových zobrazení existuje fůra, většina z nich obrázek zdeformuje k nepoznání. Nás budou zajímat jen některá z nich, takzvaná lineární zobrazení.

V minulém dílu jsme nahlédli, že prostor R^d je uzavřený na součet a násobení skalárem. Od lineárního zobrazení budeme požadovat něco podobného, konkrétně budeme chtít, aby pro všechny vektory x, y a skaláry a platilo:

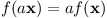
Tyto vlastnosti splňují zobrazení, která obrázek otáčí, zrcadlově převrací nebo v některých směrech roztahují, případně kombinují více těchto operací. Podívejte se na následující příklady zobrazení a rozmyslete si, že tomu tak skutečně je.

Úkol 1 – Nelineární zobrazení [2b]

Najděte příklad zobrazení v R², které není lineární. Ideálně takové, jehož chování lze popsat slovy, nikoliv pouze funkčním předpisem. Nelinearitu ukažte na konkrétních dvou vektorech, respektive vektoru a skaláru.

Báze

Nyní na chvíli odbočme a vraťme se k minulému dílu, kde jsme zkoumali generátory. Zjistili jsme, že když jsou lineárně závislé, pak lze některé z nich odebrat a jejich lineární obal se nezmění. To je občas nepraktické, proto od nich mnohdy nezávislost budeme požadovat.

Jsou-li generátory prostoru U lineárně nezávislé, řekneme, že tvoří bázi prostoru U. Poté lze každý vektor v∈U vyjádřit jako lineární kombinaci bázických vektorů díky tomu, že generují prostor U. Tato lineární kombinace je navíc jednoznačná, neboť jsou lineárně nezávislé.

Jednu možnou bázi prostoru R^d tvoří jednotkové vektory, které jsme již zmínili minule. Teď se nám bude hodit zavést pro ně značení: Jednotkový vektor, který má jedničku na i-té pozici, budeme značit e_i. Dimenzi vektoru nijak neudáváme, odvodíme ji z kontextu. Například v R³ by byl vektor e₂ roven (0, 1, 0)^⊤.

Báze složená z jednotkových vektorů se nazývá kanonická. Vyjádřit vektor v = (v₁,…,v_n)^⊤ pomocí této báze je jednoduché:

Popis zobrazení

Zpět k lineárním zobrazením. Naším cílem je popsat zobrazení f co nejjednodušším způsobem. Vypisovat obrazy f(x) pro každý možný vzor x totiž moc zábavně nezní. Zobrazení ovšem nemůže být úplně libovolné, linearita jej dost omezuje. Mělo by tedy stačit uvést obrazy jen pro pár vektorů, zbytek pak již bude jednoznačně určen.

Asi není překvapením, že si jako vzory zvolíme generátory prostoru, který transformujeme. A protože chceme mít vzorů co nejméně, zvolíme si je tak, aby byly lineárně nezávislé. Hle, báze!

Jak jsme nahlédli výše, každý vektor v lze vyjádřit jako lineární kombinaci bázických vektorů. Pokud budeme znát jejich obrazy, zvládneme díky linearitě spočítat také obraz v:

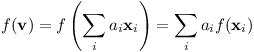
Jinými slovy, lineární zobrazení je jednoznačně určeno tím, kam se zobrazí bázické vektory.

Matice

Zatímco vektor je seznam čísel, matice je tabulka čísel. Lze na ni také pohlížet jako na seznam vektorů.

Matice využijeme k zápisu lineárního zobrazení. Vezmeme vektory kanonické báze, tedy jednotkové vektory, a jejich obrazy zapíšeme do sloupců matice.

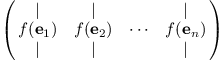
Matice pro transformace obrázků by vypadaly následovně:

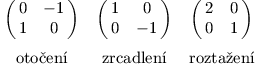
Zkuste vymyslet, jak by vypadala matice, která obrázek otočí o úhel α proti směru hodinových ručiček. Řešení najdete na konci textu.

Označme A matici lineárního zobrazení f. Rádi bychom nadefinovali součin matice a vektoru tak, abychom mohli psát f(v) = Av. Již víme, jak zapsat vektor v pomocí kanonické báze. Také umíme vyjádřit obraz vektoru pomocí obrazů bázických vektorů. Můžeme tedy spočítat, jak by měl vypadat obraz vektoru v:

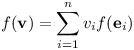
v_i je složka vektoru v, f(e_i) je zase sloupec matice A. Součin matice s vektorem spočítáme tedy tak, že vynásobíme první složku vektoru s prvním sloupcem matice, k tomu přičteme součin druhé složky s druhým sloupcem a tak dále.

Skládání zobrazení

Nyní uvažme dvě zobrazení f, g. Zobrazení f reprezentujeme maticí A, g zase maticí B. Zajímalo by nás, jak se chová složené zobrazení, kde nejprve aplikujeme f a poté g. Transformací vektoru v získáme g(f(v)) = B(Av). Nešlo by totéž zapsat jako (BA)v? Tedy nejprve spočítat jednu matici, která popíše složené zobrazení?

Pojďme vymyslet, jak by taková matice měla vypadat. Ve sloupcích by měla mít obrazy bázických vektorů. Matice A již obsahuje jejich obrazy podle f. Matice B umí jakýkoli vektor zobrazit podle g. Necháme-li tedy maticí B zobrazit sloupce A, získáme hledanou matici.

Tímto jsme tedy odvodili, jak by mělo vypadat maticové násobení. Sloupec matice BA získáme jako lineární kombinaci sloupců z B, kde jako koeficienty použijeme složky příslušného sloupce z A.

Následující schéma nabízí ještě jiný pohled. Vlevo je matice B, nahoře A, vpravo dole jejich součin BA. Jednu složku součinu získáme jako skalární součin příslušného řádku B a sloupce A.

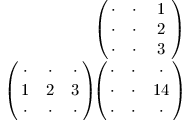
Maticí m×n myslíme matici s m řádky a n sloupci. Aby měl maticový součin AB smysl, musí být A∈R^m×p a B∈R^p×n, jinými slovy A musí mít tolik sloupců, co B řádků. Důvod je patrný ze schématu výše, oba vektory ve skalárním součinu musí mít stejnou délku.

Ještě pojďme zapsat toto schéma matematicky. Označme a_ij složku matice A∈R^m×p v i-tém řádku a j-tém sloupci, obdobně b_ij složku B∈R^p×n. Poté složku matice AB spočteme takto:

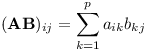
Vlastnosti maticového násobení

Pozor na to, že maticové násobení není komutativní, tedy AB není nutně rovno BA. Jednak se může stát, že po prohození nebudou mít matice vhodné rozměry. Ovšem i pokud ano, může být výsledek jiný. Pokud obrázek roztáhneme ve vodorovném směru a poté otočíme, získáme jiný obrázek, než když tyto operace provedeme v opačném pořadí. Zkuste roznásobit příslušné matice a ověřit početně.

Při skládání tří a více zobrazení ovšem nezáleží na pořadí, v jakém skládáme. Maticové násobení je tedy asociativní: (AB)C = A(BC). Jak to dokázat?

Výše jsme uvedli vzorec pro výpočet (AB)_ij. Zkuste podobným způsobem vyjádřit složku ((AB)C)_ij a (A(BC))_ij. Obě vyjádření by se měla rovnat. Nebudete-li si vědět rady, přelistujte na konec textu.

Také platí A (B + C) = AB + AC, přičemž sčítání matic probíhá podobně jako u vektorů jednoduše po složkách. Důkaz je velmi podobný důkazu asociativity.

Zajímavou maticí je jednotková matice, která má ve sloupcích jednotkové vektory. Jednotkovou matici značíme E, případně E_n, chceme-li vyjádřit její velikost. Protože zobrazuje vektory kanonické báze na sebe samé, násobení jednotkovou maticí se chová invariantně: EA = A. Dokonce i naopak, protože jednotkové vektory se zobrazí na sloupce matice A: AE = A.

Násobení matic n×n podle definice má časovou složitost Θ(n³). Existují však sofistikované algoritmy, které to zvládají rychleji. Za zmínku stojí Strassenův algoritmus. Je založený na přístupu Rozděl a panuj a zvládne vynásobit matice pomocí 7 součinů matic velikosti n/2×n/2. To vede ke složitosti Θ(n^{log₂ 7}) ≈ Θ(n^2.807) Tento algoritmus se ovšem vyplatí jen pro větší matice. Zajímá-li vás, jak přesně funguje, nahlédněte do kapitoly 10.5 v Průvodci.

Využití maticového násobení

Matice se hodí i v algoritmech, které s transformacemi obrázků nikterak nesouvisí. Nejprve se podíváme na výpočet Fibonacciho čísel. To je posloupnost s prvními členy F₀ = 0, F₁ = 1 a rekurentním vztahem F_n+2 = F_n + F_n+1, dostáváme tedy 0, 1, 1, 2, 3, 5, 8, 13, 21, …

Naším cílem bude sestavit matici, která nám vyrobí další člen v posloupnosti. Potřebujeme tedy vektorovou reprezentaci členu F_n. Protože se vždy sčítají dva členy, budeme si pamatovat i F_n+1. Naše reprezentace čísla F_n tedy bude vektor:

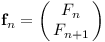
Hledaná matice Q musí splňovat:

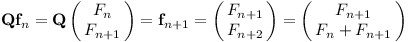
Úkol 2 – Fibonacciho čísla [5b]

Sestavte matici Q. Poté napište algoritmus, který dostane zadané číslo n a spočítá F_n. Napovíme, že to jde lépe než v lineárním čase. Můžete použít svůj oblíbený programovací jazyk, ale postačí i pseudokód.

Ještě zmiňme jedno využití v grafových algoritmech. Mějme graf s n vrcholy zadaný maticí sousednosti. To je matice A∈R^n×n, která má na pozici A_ij jedničku, pokud vede hrana z vrcholu i do vrcholu j, jinde jsou nuly. Jaký význam má matice A² = AA? Dle definice:

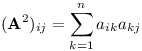
Jak tuto sumu interpretovat? Započítám jedničku za každou dvojici hran, kde první vede z i do k a druhá z k do j. Výraz tedy určuje počet sledů délky 2 vedoucích z i do j. Pro připomenutí, sled označuje jakoukoli procházku po grafu, ve které se na rozdíl od cesty mohou opakovat vrcholy nebo dokonce hrany. Třeba výraz (A²)_ii rozhodně nemusí být nulový.

Obdobně (A^ℓ)_ij by byl počet sledů délky ℓ.

Úkol 3 – Dosažitelnost [5b]

Popište, jak upravit předchozí postup, aby spočítal matici dosažitelnosti. Tato matice na pozici i,j obsahuje jedničku právě tehdy, pokud existuje orientovaná cesta z i do j. Vyhněte se počítání s obrovskými čísly.

Matice a soustavy rovnic

Pomocí maticového násobení můžeme elegantně zapsat soustavu rovnic:

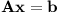
Také Gaussovu eliminaci můžeme zapsat maticově, elementární úpravy budou pracovat s řádky matice. Při ručním počítání nám maticový zápis ušetří psaní, nemusíme opisovat plusy a neznámé.

Minule jsme narazili na soustavy, které neměly jednoznačné řešení nebo řešení neměly vůbec. K této situaci došlo, pokud při Gaussově eliminaci vznikl řádek se samými nulami. Vzhledem k tomu, že při eliminaci k němu pouze přičítáme násobky jiných řádků, znamená to, že musel být jejich lineární kombinací. Jinými slovy řádky v matici A byly lineárně závislé.

Naopak, jsou-li řádky matice A lineárně nezávislé, pak má rovnice Ax = b vždy jednoznačné řešení. Lineární nezávislost řádků je důležitá vlastnost, na kterou ještě mnohokrát narazíme. Má proto svůj název, o matici A řekneme, že je regulární.

Pozor na to, že úvahy výše platí pouze pro soustavy se čtvercovou maticí, tedy takové, kde je počet rovnic stejný jako počet neznámých. Je-li neznámých více než rovnic, pak nám ani lineární nezávislost řádků nezajistí jednoznačnost. Naopak, je-li rovnic více, pak může řešení být jednoznačné navzdory závislým řádkům. Pojem regulární matice se také vztahuje pouze ke čtvercovým maticím.

Inverzní matice

Zobrazení nám dávají nový pohled na soustavu rovnic: Hledáme vektor x, který je maticí A zobrazen na b. Při řešení soustavy rovnic se vlastně snažíme přehrát zobrazení pozpátku. Neexistuje tedy matice, která by toto opačné zobrazení popisovala?

Matice, kterou hledáme, se nazývá inverzní a budeme ji značit A^-1. Chtěli bychom, aby její součin s A byl roven jednotkové matici. Pak bychom mohli vynásobit obě strany soustavy rovnic zleva inverzní maticí a získat explicitní vyjádření vektoru neznámých x:

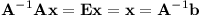
Jak inverzní matici spočítat? Tato matice by byla neznámou X v rovnici AX = E. Maticové násobení můžeme rozepsat po sloupcích. Pokud označíme x_i sloupec matice X, dostaneme pro každé i rovnici Ax_i = e_i. A tu můžeme interpretovat jako soustavu rovnic, kterou umíme vyřešit.

Jak jsme nahlédli výše, jednoznačné řešení mají pouze soustavy rovnic, ve kterých je matice A regulární. To také znamená, že inverzní matice existuje pouze k regulárním maticím.

Doteď jsme tiše předpokládali, že platí A^-1 A = A A^-1. Pro úplnost tedy předkládáme důkaz. Dejme tomu, že máme matici X, pro kterou platí AX = E. Předpokládejme, že existuje A^-1 taková, že A^-1 A = E. Chceme ukázat, že X a A^-1 jsou stejné.

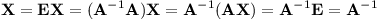
Úkol 4 – Obecná inverze [3b]

Najděte inverzní matici k

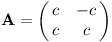
Řešení na konci textu

Matice rotace. Jaký vektor vznikne, pokud otočíme vektor (1,0)^⊤ o úhel α? Výsledný vektor bude ležet na jednotkové kružnici. Jeho souřadnice lze tedy popsat goniometrickými funkcemi, konkrétně (cosα, sinα)^⊤. Ještě potřebujeme totéž pro vektor (0,1)^⊤, jeho otočením vznikne (-sinα, cosα)^⊤.

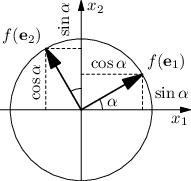
Stačí tedy umístit tyto vektory do matice:

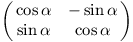
Asociativita maticového násobení. Mějme matice o rozměrech A∈R^m×p, B∈R^p×q, C∈R^q×n.

David Klement

Řešení