Čtvrtá série třicátého pátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Dostává se k vám čtvrté číslo hlavní kategorie 35. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Také na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál na lineární algebru.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: 9. dubna 2023 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo nám napíše řešení 1 teoretické úlohy nebo celého seriálu v angličtině. Pro inspiraci nabízíme anglické řešení části 3. série. Kdybyste si nebyli jistí terminologií, napište nám na english@ksp.mff.cuni.cz, rádi poradíme.
Zadání úloh
- 35-4-1: Golfový turnaj
- 35-4-2: Kevinovo velkolepé rozloučení
- 35-4-3: Házení
- 35-4-4: Hroší růže
- 35-4-S: Skalární součin
- 35-4-X1: Mnoho jamek
 35-4-1 Golfový turnaj (14 bodů)
35-4-1 Golfový turnaj (14 bodů)
Bjørn sleduje golfový turnaj a obdivuje hráče, kteří pár údery dopraví míček do vzdálené jamky. Hned by si to také zkusil, ale přestavět školní hřiště na golfové mu loni zakázali a do jeho pokojíku se nevejde ani jedna jamka s greenem.
Napadlo ho zahrát si s kamarády programátorský golf. Vymyslí si jednoduchou úlohu a budou se snažit napsat co nejkratší program, který ji vyřeší. Pojďte si také zahrát.
Programovací jazyk
Jazyk si můžete vyzkoušet ve webovém simulátoru. Tam také najdete popis jazyka.
Úkoly
- Vytvořte na zásobníku číslo 2023. (2 body)
- Na zásobníku dostanete nějaká čísla (alespoň jedno). Nahraďte je jejich součtem. (2 body)
- Na vrcholu zásobníku je číslo y ≥ 0, pod ním x. Nahraďte je mocninou xy. (2 body)
- Na zásobníku dostanete dvě kladná čísla. Nahraďte je jejich největším společným dělitelem. (2 body)
- Na zásobníku dostanete číslo 1 ≤ n ≤ 100. Nahraďte jej n-tým nejmenším prvočíslem. Například pro vstup 3 je správný výstup 5. (3 body)
- Na zásobníku dostanete posloupnost 1 ≤ n ≤ 20 čísel. Seřaďte ji od nejmenšího (na dně) po největší (na vrcholu). (3 body)
Odevzdávání
Toto je praktická úloha. Každý úkol se chová jako jeden test. Vstupní soubor obsahuje jen číslo úkolu. Jako výstup odevzdejte svůj program. Vyzkoušíme ho na našich testovacích datech a pokud odpoví správně, přidělíme mu body.
Počet bodů záleží na délce programu měřené ve znacích (mezery nepočítáme). Program stejně dlouhý jako naše referenční řešení dostane plný počet bodů. Delší programy dostanou méně, ale aspoň 30 % maxima. Pokud se vám podaří najít kratší program, můžete dostat až 30 % bodů navíc.
 35-4-2 Kevinovo velkolepé rozloučení (9 bodů)
35-4-2 Kevinovo velkolepé rozloučení (9 bodů)
Kevina přiletěla navštívit jeho kamarádka Zuzka, která bydlí v Americe. Užili si spolu spoustu zábavy, ale zítra Zuzka odlétá domů. Kevin se chce se Zuzkou rozloučit nějakým pompézním způsobem. Po Zuzčině odjezdu na letiště napsal na střechu svého domu zprávu na rozloučenou, kterou si bude moci Zuzka přečíst z letadla.
Když zprávu dopsal, všiml si, že slova ve zprávě jsou v opačném pořadí. Barva už ale zaschla a nejde smýt. Kevin se tedy rozhodl, že zprávu opraví zpřeházením střešních tašek. Na jedné tašce je jedno písmeno, případně je prázdná jako mezera. Tašky jsou ale těžké a Kevin unese jenom jednu najednou. Navíc nelze tašky odkládat na střechu jen tak bokem, takže má Kevin jedinou možnost: vždy si vybrat dvě tašky a ty prohodit.
Pomozte Kevinovi vymyslet algoritmus, který zjistí, jak přehodit pořadí slov ve zprávě. Na střeše se však nenachází žádný počítač, takže Kevin jej bude vyhodnocovat z hlavy. Zvládne si zapamatovat jen konstantní množství čísel, velkých řádově jako délka zprávy.
Váš algoritmus tedy smí používat jen konstantní množství paměti. Může se zeptat na písmeno na dané pozici a vypsat indexy dvou tašek, které má Kevin prohodit. Hledáme algoritmus s co nejkratším časem výpočtu.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 35-4-3 Házení (11 bodů)
35-4-3 Házení (11 bodů)
 Robert se rozhodl zapsat si jako tělocvik basketbal a první hodinu semestru začali házením na koš.
Jenže to není tak jednoduché. Z Vánoc ještě zbyly v tělocvičně zavěšené různé ozdoby a nikdo se nenamáhal je sundat.
Robert tak musí nejen hodit míč tak, aby skončil v koši, ale i tak, aby v letu nesrazil žádnou z ozdob.
Jelikož bude na koš házet ještě další hodinu, tak by se u toho rád co nejméně nadřel, tedy aby počáteční rychlost,
kterou míč hodí, byla co nejmenší.
Robert se rozhodl zapsat si jako tělocvik basketbal a první hodinu semestru začali házením na koš.
Jenže to není tak jednoduché. Z Vánoc ještě zbyly v tělocvičně zavěšené různé ozdoby a nikdo se nenamáhal je sundat.
Robert tak musí nejen hodit míč tak, aby skončil v koši, ale i tak, aby v letu nesrazil žádnou z ozdob.
Jelikož bude na koš házet ještě další hodinu, tak by se u toho rád co nejméně nadřel, tedy aby počáteční rychlost,
kterou míč hodí, byla co nejmenší.
Jenže to už je docela oříšek a Robertovi se po rozcvičce sestávající z běhání a klikování nechce přemýšlet, takže je to na vás.
Situaci si můžeme představit jako 2D mřížku, kde x-ová osa je horizontální spojnice mezi Robertem a košem a y-ová osa jde do výšky. Vzdálenost mezi sousedními body mřížky odpovídá 1 m.
Robert hází z bodu (0,0) a koš se nachází v bodě (M, 0), tedy předpokládáme, že Robert bude házet ze stejné výšky, jako je koš. Zároveň se v místnosti nachází N ozdob, které si můžeme představit jako obdélníky s rohovými políčky v bodech (x1,y1), (x1,y2), (x2,y1) a (x2,y2) – tedy hrany obdélníka jsou zarovnané s osami.
Míč si můžeme představit jako hmotný bod, který je vržen pod úhlem α s počáteční rychlostí V0 (formálně V0 je absolutní hodnota vektoru počáteční rychlosti). Míč se dále pohybuje v souladu s fyzikálními zákony, kdy vliv odporu vzduchu můžeme zanedbat. Tíhové zrychlení uvažujeme 9.81 ms-2.
Hod je považován za platný, pokud míč netrefí žádnou z ozdob a skončí v koši. Trajektorie míče tedy musí procházet bodem (M, 0) a nesmí projít vnitřkem žádného obdélníku určujícího ozdobu. Dotknout se hrany může.
Najděte α a V0 takové, že hod s těmito počátečními podmínkami je platný a zároveň V0 je minimální možné.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete číslo T udávající počet hodů, které máte vyřešit.
Pro každý hod pak na prvním řádku dostanete mezerou oddělená celá čísla N a M – počet ozdob a x-ovou souřadnici koše. Na každém z následujících N řádků dostanete čtyři celá čísla x1i, y1i, x2i, y2i oddělená mezerou, která udávají souřadnice rohů ozdoby.
Formát výstupu: Na výstup vypište dvě mezerou oddělená čísla α (ve stupních) a V0 (v ms-1). Pozor, tato čísla téměř určitě nebudou celá, dbejte tedy na jejich přesnost. Vaše řešení bude uznané za správné, pokud relativní odchylka od vzorového řešení bude nejvýše 0.01 %. Můžete předpokládat, že řešení existuje.
2 2 100 35 10 60 15 10 30 85 45 1 1000 400 200 800 400
45 31.321 38.660 100.276
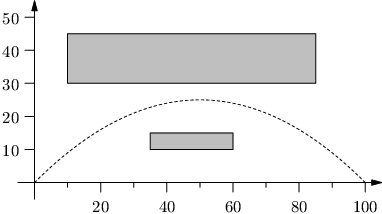
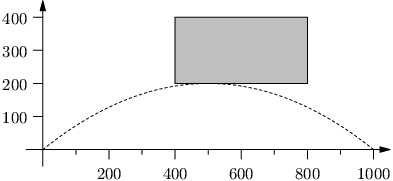
 35-4-4 Hroší růže (11 bodů)
35-4-4 Hroší růže (11 bodů)
Filip má za domem N políček posetých růží hroší (Rosa chinensis `Hippo'). Čaj z jejích květů (též nazývaný hrůžový) navrací vzpomínky na dávné květnové večery.
Hroší růže je poměrně náročná rostlina, takže je potřeba ji zavlažovat téměř každý den. Při té příležitosti se Filip rozhodl ze zalévání políček udělat zábavnou činnost.
Postavil systém M skluzavek, kde i-tá skluzavka vede z vi-tého políčka na wi-té políčko. Ačkoliv to byla jistě výhodná investice, skluzavky jsou poměrně drahá komodita, a proto z každého políčka vede nejvýše jedna skluzavka.
Pokud vede skluzavka z políčka a na políčko b, Filip se po ní může sklouznout. Jelikož ale skluzavky bývají nakloněné, v opačném směru by musel Filip po skluzavce šplhat, čímž by ji ale zašpinil hlínou z políček, a tak to nedělá. Přesto může být systém skluzavek navržený tak, že skluzavka povede také z políčka b na políčko a.

Filipův způsob zalévání probíhá každý den následovně: vybere si počáteční a koncové políčko a následně se mezi nimi klouže po skluzavkách, které vybírá vždy z aktuálního políčka. Po cestě nezapomíná zavlažovat políčka. Takto se dopravuje tak dlouho, dokud neskončí na koncovém políčku.
Filip zjistil, že se v některých případech nezvládne z jednoho políčka doklouzat na druhé. Rád by proto přidal co nejméně skluzavek, aby se mu to podařilo. Pomůžete mu s tím?
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
Na vstupu dostanete hodnoty N, M. Můžete předpokládat, že políčka jsou očíslovaná 1 až N. Dále dostanete specifikaci systému skluzavek, což je M dvojic čísel ve formátu vi wi.
Na výstup vypište jediné číslo – nejmenší počet skluzavek, který je potřeba k tomu, aby se z libovolného políčka šlo doklouzat na libovolné jiné.
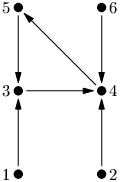
Na obrázku nahoře je potřeba doplnit alespoň tři skluzavky.
Jedním z řešení je například trojice 5 6, 1 2 a 6 1.
 35-4-X1 Mnoho jamek (10 bodů)
35-4-X1 Mnoho jamek (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
Tato úloha vychází z první úlohy v této sérii Golfový turnaj. Odevzdávání a hodnocení funguje stejným způsobem.
Na zásobníku dostanete posloupnost 1 ≤ n ≤ 800 čísel. Seřaďte ji od nejmenšího (na dně) po největší (na vrcholu).
Připomínáme, že v jedné chvíli se na zásobníku smí nacházet maximálně 1000 čísel a program musí doběhnout do 1 milionu kroků.
 35-4-S Skalární součin (15 bodů)
35-4-S Skalární součin (15 bodů)
Právě čtete čtvrtý díl seriálu. Pokud jste předchozí díly neřešili, pro pochopení následujících odstavců je vhodné si je přinejmenším přečíst. Navíc je stále možné odevzdávat úlohy z nich za polovinu bodů.
Transpozice
Transpozici jsme již nakousli v prvním dílu. Nyní ji budeme používat více, proto si ji nadefinujeme pořádně.
Máme-li matici A o rozměrech m×n, její transpozice A⊤ je matice n×m. Vznikne překlopením matice A podél hlavní diagonály, tedy diagonály vedoucí z levého horního rohu. Prvek na pozici (i, j) se v transponované matici bude nacházet na pozici (j, i).
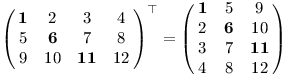
Skalární součin
Dosud neumíme zjistit, jakou polohu vůči sobě mají dva vektory, například jaký svírají úhel. S pomocí skalárního součinu to zvládneme, cesta však bude dlouhá a klikatá. Objevíme na ní však i další, možná ještě hezčí geometrické vlastnosti.
Skalární součin dvou vektorů budeme značit ⟨x,y⟩. Spočítáme jej tak, že vektory vynásobíme po složkách a výsledky sečteme. Pochopitelně musí mít oba vektory stejné rozměry. Dostaneme skalár, odtud také pochází název. Matematicky:
| n |
| i=1 |
Poslední podoba využívá maticové násobení. Vektory jsou standardně sloupcové, transpozicí vektoru x s n složkami vznikne matice 1×n.
Snadno nahlédneme následující rovnosti:
- ⟨x,y⟩ = ⟨y,x⟩
- ⟨x + y,z⟩ = ⟨x,z⟩ + ⟨y,z⟩
- ⟨a x,y⟩ = a ⟨x,y⟩
Díky symetrii (1) platí linearita (2, 3) i pro druhý vektor v součinu.
Přidáme ještě čtvrtou vlastnost: ⟨x,x⟩ ≥ 0. Proč platí? Při násobení složek vznikají druhé mocniny, které jsou nezáporné. Navíc to znamená, že nulový výsledek nastane jen pro x = 0.
Skalární součin se většinou definuje axiomaticky. Nepředepisujeme tedy konkrétní vzorec, ovšem povolíme jakýkoli vztah splňující uvedené vlastnosti. My se však omezíme na ten výše uvedený, tedy standardní skalární součin.
Norma
Nezápornost skalárního součinu vektoru se sebou samým nám umožní definovat normu neboli velikost vektoru:
Pro standardní skalární součin norma odpovídá běžné délce, kterou bychom změřili pravítkem.
Občas vektor používáme jen pro určení směru a na jeho velikosti nám nezáleží. Pak se může hodit vektor normalizovat tak, aby měl jednotkovou délku. Toho dosáhneme jednoduše, vektor vydělíme jeho normou.
Také můžeme změřit vzdálenost vektorů jako normu jejich rozdílu ‖x - y‖.
Kolmost
K měření úhlů nám stále kus chybí, ovšem nyní se naučíme poznat alespoň ten pravý. Tvrdíme, že vektory x a y jsou na sebe kolmé právě tehdy, když je jejich skalární součin nulový. Pokud jste se již s tímto tvrzením setkali ve škole, nejspíše vám bylo předloženo bez důkazu. Zde se o něj pokusíme.
Pomůže nám Pythagorova věta. Její znění nejspíše znáte: Pro pravoúhlý trojúhelník s odvěsnami délek a, b a přeponou délky c platí vztah:
Trochu méně známá je věta opačná. Platí-li vztah výše pro délky stran trojúhelníka, svírají odvěsny pravý úhel.
Nyní sestavíme vektorovou podobu této rovnosti. Odvěsny označíme pomocí vektorů x, y. Přepona pak bude x - y. Odvoďme její délku:
| ‖x - y‖2 | = ⟨x - y,x - y⟩ |
| = ⟨x,x - y⟩ - ⟨y,x - y⟩ | |
| = ⟨x,x⟩ - ⟨x,y⟩ - ⟨y,x⟩ + ⟨y,y⟩ | |
| = ‖x‖2 - 2⟨x,y⟩ + ‖y‖2 |
Předpokládejme ⟨x,y⟩ = 0. Pak dle výpočtu výše platí ‖x - y‖2 = ‖x‖2 + ‖y‖2 a z opačné Pythagorovy věty vyplývá, že vektory x, y jsou sebe kolmé.
Nyní naopak předpokládejme kolmost. Dle Pythagorovy věty ‖x - y‖2 = ‖x‖2 + ‖y‖2, což nutně znamená 2⟨x,y⟩ = 0.
Dokázali jsme oba směry, ekvivalence tedy platí.
Ortogonální báze
Kolmosti ihned využijeme, nejdříve ovšem potřebujeme pár definic. Máme-li systém vektorů takových, že každé dva jsou na sebe kolmé, nazveme ho ortogonální. Pokud navíc každý vektor znormalizujeme, dostaneme ortonormální systém.
Tento systém samozřejmě může tvořit i bázi. Podmínku lineární nezávislosti dokonce ortonormální systémy splňují automaticky. Důkaz vynecháme, složitý však není.
Ortonormální báze nám zjednoduší hledání souřadnic. Dosud jsme je počítali pomocí Gaussovy eliminace, tedy v čase O(n3). Jde to však rychleji.
Uvažme kanonickou bázi, která ortonormalitu splňuje. Souřadnice [x]kan najdeme jednoduše, první složka souřadnic odpovídá první složce x atd. Na totéž lze pohlížet i jinak: První složku souřadnic dostaneme jako skalární součin prvního bazického vektoru s x. I kdybychom bazické vektory přeházeli, stále bychom dostali správný výsledek.
Totéž funguje obecně. Mějme prostor U a jeho ortonormální bázi B = {b1, …, bn}. Souřadnice [x]B budou mít v i-té složce hodnotu ⟨x,bi⟩. Zapsáno jako lineární kombinace:
| n |
| i=1 |
Pojďme to dokázat. Vektor x určitě lze zapsat jako lineární kombinaci bazických vektorů:
| n |
| i=1 |
Naším cílem je ukázat, že ai = ⟨x,bi⟩. Rozepišme tedy skalární součin:
| ⟨x,bi⟩ | = ⟨∑
| ||
= ∑
| |||
| = ∑j ≠ i aj ⟨bj,bi⟩ + ai ⟨bi,bi⟩ | |||
| = ∑j ≠ i aj ·0 + ai ·1 = ai |
Sumu jsme rozdělili na dva případy. Pokud j ≠ i, jsou vektory bi a bj kolmé z definice ortonormální báze. Naopak pro j = i dostáváme skalární součin vektoru se sebou samým.
Koeficienty ⟨x,bi⟩ se nazývají Fourierovy koeficienty a díky nim umíme souřadnice najít v čase O(n2).
Projekce
Fourierovy koeficienty nám také odkryjí geometrický význam skalárního součinu. Uvažme přímku procházející počátkem, popíšeme ji normalizovaným vektorem u. Dále mějme bod x. Hledáme bod xU na přímce u, který je nejblíže bodu x, takzvanou projekci bodu x na přímku u.
Z geometrie víme, že projekci lze najít tak, že z bodu x vedeme kolmici na přímku u. Použijeme podobný princip. Přidáme normalizovaný vektor n kolmý na u a rozložíme x jako lineární kombinaci těchto dvou vektorů:
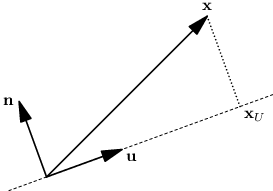
Hledaná projekce je xU = ⟨x,u⟩ u. Také umíme spočítat vzdálenost bodu x od přímky u jako ‖x - xU‖.
Skalární součin ⟨x,u⟩ tedy vyjadřuje velikost projekce xU. Takto to platí jen pro normalizovaný vektor u, v plné obecnosti je velikost projekce ⟨x,u⟩ / ‖u‖.
S trochou goniometrie zvládneme konečně spočítat úhel α mezi vektory x a u:
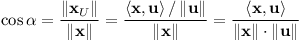
Projekci jsme odvozovali ve dvou dimenzích, tentýž vzorec ale platí i v prostorech s více dimenzemi. Vektory x a u totiž vždy leží v jedné rovině, takže všechny naše úvahy fungují stejně.
Podobně jako na přímku můžeme projektovat na rovinu či jiný prostor. Stačí tento prostor popsat ortonormální bází, spočítat projekci do směru každého bazického vektoru a tyto projekce sečíst.
Úkol 1 – Mnohoúhelník [4b]
Dostanete zadané vrcholy p1, …, pn konvexního mnohoúhelníku v rovině a bod x.
Popište, jak rozhodnout, zda leží bod x uvnitř mnohoúhelníku. Určete časovou složitost svého řešení.
Ortogonalizace
Již známe výhody ortonormální báze. Ovšem jak ji získat? K tomu nám poslouží Gramova-Schmidtova ortogonalizace (ve skutečnosti jde o ortonormalizaci, ovšem tento název je zažitý).
Mějme lineárně nezávislé vektory x1, …, xn. Chceme získat ortonormální systém vektorů y1, …, yn se stejným lineárním obalem.
Vektor y1 získáme normalizací vektoru x1. Vektor y2 musí být kolmý na y1. Od vektoru x2 tedy odečteme jeho projekci na y1, výsledek normalizujeme a uložíme jako y2. Obdobně postupujeme dále, vždy odečteme projekci na všechny předchozí vektory.
Zapsáno matematicky, yk spočítáme následovně:
| k-1 |
| i=1 |
| nk |
| ‖nk‖ |
Úkol 2 – Vzdálenost od roviny [6b]
Určete vzdálenost bodu x = (6, 3, 3)⊤ od roviny ρ, jejíž body lze vyjádřit ve tvaru c + a1 u1 + a2 u2, kde:
| c | = (1, 2, 3)⊤ |
| u1 | = (2, -3, 6)⊤ |
| u2 | = (4, 4, 2)⊤ |
Pokud použijete vzorec neuvedený v tomto textu, musíte jej odvodit.
Ortogonální doplněk
Na začátku jsme nahlédli, že standardní skalární součin lze vnímat také jako maticové násobení. Výraz Ax počítá najednou několik skalárních součinů, jedna složka výsledku odpovídá skalárnímu součinu jednoho řádku matice A s vektorem x. Pokud vyjdou všechny skalární součiny nulové, tedy pokud Ax = 0, je vektor x kolmý na všechny řádky matice A. Zároveň si vzpomeňte, že jsme v posledním dílu definovali jádro matice A přesně jako množinu vektorů x, které tuto rovnici splňují.
Dostáváme tak nový pohled na jádro jako na množinu vektorů kolmých na řádky matice. Nejen to, vektory jádra jsou kolmé dokonce na všechny vektory z řádkového prostoru, protože lineární kombinace vektorů kolmých na x bude opět kolmá na x.
Totéž platí v opačném směru, každý vektor řádkového prostoru je kolmý na všechny vektory jádra. Báze obou prostorů se navzájem doplňují, dohromady tvoří bázi celého prostoru Rn, kde n je dimenze x. Říkáme, že řádkový prostor je ortogonální doplněk jádra a naopak.
Tímto dostáváme návod, jak najít množinu vektorů kolmých k nějakému podprostoru U. Stačí dát bázi U do řádků matice a vyřešením soustavy rovnic najít její jádro.
Metoda nejmenších čtverců
Kromě výpočtu vzdálenosti geometrických objektů má projekce ještě jedno využití, totiž hledání přibližných řešení soustav rovnic. Uvažme soustavu Ax = b, která nemá řešení. Můžeme však najít takové b', pro které řešení existuje a které je co nejblíže původnímu b.
Z minulého dílu víme, že řešení existuje, pokud pravá strana leží ve sloupcovém prostoru, což nám dává podmínku b'∈S(A). Hledáme projekci, takže b' - b musí být kolmé na S(A), jinými slovy musí ležet v jeho ortogonálním doplňku. Víme, že jádro je doplňkem řádkového prostoru, zde však máme sloupcový prostor. Není problém, transpozicí zaměníme sloupce za řádky. Hledaným doplňkem je proto ker(A⊤). Dostáváme tedy rovnici b' - b ∈ker(A⊤), kterou stačí rozepsat:
| A⊤(b' - b) | = 0 |
| A⊤(Ax - b) | = 0 |
| A⊤Ax | = A⊤b |
Matici A⊤A můžeme vyčíslit, stejně tak vektor A⊤b. Dostaneme novou, takzvanou normální soustavu rovnic, která již řešení mít bude.
Tento přístup nese název metoda nejmenších čtverců, neboť minimalizujeme vzdálenost ‖b' - b‖. Minimum se nabude pro stejné b' jako minimum druhé mocniny tohoto výrazu, a to není nic jiného než součet druhých mocnin rozdílů složek b' a b.
Úkol 3 – Fyzikální měření [5b]
David měřil, jak rychle se vypařuje tekutý dusík z láhve, ve které jej skladuje. Láhev měl položenou na váze a zaznamenával hmotnost v průběhu času.
| m / g | 67 | 66 | 63 | 62 | 60 |
| t / s | 0 | 3 | 10 | 14 | 20 |
Nyní by rád zjistil, za jak dlouho se všechen dusík vypaří. Předpokládejte, že závislost hmotnosti na čase lze odhadnout lineární funkcí, viz čárkovaná přímka na obrázku. Spočítejte rychlost vypařování metodou nejmenších čtverců a odpovězte mu.
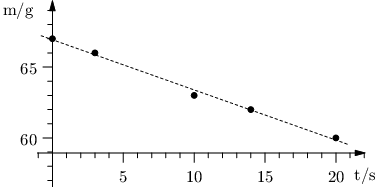
Mimochodem, metoda minimalizuje druhé mocniny vertikálních vzdáleností mezi přímkou a body.
Vizualizace
Tento díl při důkazech využíval převážně algebraické operace, které se pro psaný text hodí více. Mnohé však lze nahlédnout i vizuálně. Pokud neznáte, velmi doporučujeme sérii videí od 3Blue1Brown, zejména pak video na skalární součin, které na něj nabízí úplně jiný pohled.