Recepty z programátorské kuchařky
Rekurzivní funkce a dynamické programování
Aktuální verze kuchařky: listopad 2023
Rekurzivní funkce je taková funkce, která při svém běhu volá sama sebe, často i více než jednou. To typicky vede na exponenciální časovou složitost algoritmu.
Dynamické programování je technika, kterou lze z pomalého rekurzivního algoritmu vyrobit pěkný polynomiální, tedy až na výjimečné případy. A jako ukázku si představíme algoritmus, který nalezne délky nejkratších cest mezi každými dvěma městy na mapě.
Ale nepředbíhejme, nejdříve se podíváme na jednoduchý příklad rekurze.
Fibonacciho čísla
Budeme počítat n-té číslo Fibonacciho posloupnosti. To je posloupnost, jejíž nultý člen je nula, první je jednička (F0 = 0, F1 = 1) a každý další člen je součtem dvou předchozích (Fn = Fn-1 + Fn-2 pro n>1). Začíná takto:
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | … |
Pro nalezení n-tého členu (v našem značení Fn) si napíšeme rekurzivní
funkci fib(n), která bude postupovat přesně podle definice – zeptá se sama sebe rekurzivně, jaká jsou dvě předchozí
čísla, a pak je sečte. Možná více řekne program:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
function fib(n: integer): integer;
begin
if n == 0 then
fib := 0
else if n == 1 then
fib := 1
else
fib := fib(n-1) + fib(n-2)
end;
To, jak funkce volá sama sebe, si můžeme snadno nakreslit třeba pro výpočet čísla F5:
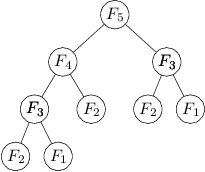
Vidíme, že se program rozvětvuje, což tvoří strom volání. V každém vrcholu tohoto stromu trávíme konstantní čas, takže časová složitost celého algoritmu je až na konstantu rovna počtu vrcholů tohoto stromu. Kolik to je, spočítáme jednoduchou úvahou.
Každý vrchol stromu vrací hodnotu, která je součtem hodnot v jeho synech. Proto je hodnota v kořeni rovna součtu hodnot v listech. V listech jsou ovšem jedničky (F1 a F2), takže listů musí být právě Fn a všech vrcholů dohromady aspoň Fn.
Proto na spočítání n-tého Fibonacciho čísla spotřebujeme čas alespoň takový, kolik je ono číslo samo. Ale jak velké takové Fn vlastně je? Můžeme třeba využít toho, že
z čehož indukcí dokážeme
Funkce Fibonacci má tedy alespoň exponenciální časovou složitost, což
není nic vítaného.
Jak najít efektivnější algoritmus? Všimneme si, že některé podstromy jsou shodné. Zřejmě to budou ty části, které reprezentují výpočet stejného Fibonacciho čísla – v našem příkladě třeba třetího. Tyto výpočty opakujeme stále dokola.
Nenabízí se proto nic snazšího, než si jejich výsledky uložit a pak je kdykoliv vytáhnout jako pověstného králíka z klobouku ( Právě zde je zmínka o králících příhodná. Legenda o Fibonacciho číslech vypráví, že k jejich objevu došlo při výzkumu rozmnožování králíků, kdy první dva měsíce měl 1 pár, další měsíc měl 2 páry, pak 3, pak 5, …) s minimem námahy.
Bude nám k tomu stačit jednoduché pole P o n prvcích, které na počátku inicializujeme hodnotami značícími nespočítané hodnoty. Kdykoliv budeme chtít spočítat některý člen, nejdříve se podíváme do pole, zda jsme ho již jednou nespočetli. A naopak jakmile hodnotu spočítáme, hned si ji do pole poznamenáme:
P = [None] * (MaxN + 1)
P[0] = 0; P[1] = 1
def fibonacci(n):
if P[n] is None:
P[n] = fibonacci(n-1) + fibonacci(n-2)
return P[n]
function fibonacci(n: integer): integer;
var P: array[1..MaxN] of integer;
begin
if n = 0 then
P[n] := 0
else if n = 1 then
P[n] := 1
else if P[n] = 0 then
begin
P[n] := fibonacci(n-1) + fibonacci(n-2)
end;
fibonacci := P[n]
end;
Podívejme se, jak vypadá strom volání nyní:
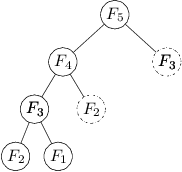
Na každý člen posloupnosti se tentokrát ptáme maximálně dvakrát – k výpočtu ho
potřebují dva následující členy. To ale znamená, že funkci Fibonacci
zavoláme maximálně 2n-krát, čili jsme touto jednoduchou úpravou zlepšili
exponenciální složitost na lineární.
Zdálo by se, že abychom získali čas, museli jsme obětovat paměť, ale to není tak úplně pravda. V prvním příkladu sice nepoužíváme žádné pole, ale při volání funkce si musíme zapamatovat některé údaje, jako je třeba návratová adresa, parametry funkce a její lokální proměnné, a na to samotné potřebujeme určitě paměť lineární s hloubkou vnoření, v našem případě tedy lineární s n.
Určitě vás už také napadlo, že n-té Fibonacciho číslo se dá snadno spočítat i bez rekurze. Stačí si prvky posloupnosti počítat postupně od začátku – kdykoliv známe F1…k (všechny prvky posloupnosti až do indexu k), dokážeme snadno spočítat i Fk+1:
def fibonacci2(n):
if n == 0:
return 0
a = 0; b = 1
while n > 1:
(a, b) = (b, a+b)
n -= 1
return b
function fibonacci2(n: integer): integer;
var i, a, b, pomocna: integer;
begin
if n = 0 then
fibonacci2 := 0
else begin
a := 0; b := 1;
while n > 1 do begin
pomocna := a + b;
a := b;
b := pomocna;
dec(n);
end;
fibonacci2 := b
end;
end;
Zopakujme si, co jsme postupně udělali – nejprve jsme vymysleli pomalou rekurzivní funkci, kterou jsme zrychlili zapamatováváním si mezivýsledků. Nakonec jsme ale celou rekurzi „obrátili naruby“ a mezivýsledky počítali od nejmenšího k největšímu, aniž bychom se starali o to, jak se na ně původní rekurze ptala.
V případě Fibonacciho čísel je samozřejmě snadné přijít rovnou na nerekurzivní řešení, a díky pamatování si jen posledních dvou hodnot snížit i paměťovou složitost na konstantní.
Zmíněný obecný postup zrychlování rekurze nebo rovnou řešení úlohy od nejmenších podproblémů k těm největším funguje i pro řadu složitějších úloh a říkáme mu technika dynamického programování. Ukážeme si další problém řešitelný touto technikou.
Problém batohu
Je dáno N předmětů o hmotnostech m1,… ,mN (celočíselných) a také číslo M (nosnost batohu). Úkolem je vybrat některé z předmětů tak, aby součet jejich hmotností byl co největší, ale přitom nepřekročil M. Předvedeme si algoritmus, který tento problém řeší v čase O(MN).
Náš algoritmus bude používat pomocné pole A[0… M] a jeho činnost bude rozdělena do N kroků. Na konci k-tého kroku bude prvek A[i] nenulový právě tehdy, jestliže z prvních k předmětů lze vybrat předměty, jejichž součet hmotností je přesně i.
Před prvním krokem (po nultém kroku) jsou všechny hodnoty A[i] pro i>0 nulové a A[0] má nějakou nenulovou hodnotu, řekněme -1.
Všimněme si, jak kroky algoritmu odpovídají podúlohám, které řešíme – v prvním kroku vyřešíme podúlohu tvořenou jen prvním předmětem, ve druhém kroku prvními dvěma předměty, pak prvními třemi předměty atd.
Popišme si nyní k-tý krok algoritmu. Pole A budeme procházet od konce, tj. od i=M. Pokud je hodnota A[i] stále nulová, ale hodnota A[i-mk] je nenulová, změníme hodnotu uloženou v A[i] na k (později si vysvětlíme, proč zrovna na k).
Nyní si rozmyslíme, že po provedení k-tého kroku odpovídají nenulové hodnoty v poli A hmotnostem podmnožin z prvních k předmětů (podmnožina je v podstatě jen výběr nějaké části předmětů).
Pokud je hodnota A[i] nenulová, pak buď byla nenulová před k-tým krokem (a v tom případě odpovídá hmotnosti nějaké podmnožiny prvních k-1 předmětů), anebo se stala nenulovou v k-tém kroku.
Potom ale hodnota A[i-mk] byla před k-tým krokem nenulová, a tedy existuje podmnožina prvních k-1 předmětů, jejíž hmotnost je i-mk. Přidáním k-tého předmětu k této podmnožině vytvoříme podmnožinu předmětů hmotnosti přesně i.
Naopak, pokud lze vytvořit podmnožinu X hmotnosti i z prvních k předmětů, pak takovou podmnožinu X lze buď vytvořit jen z prvních k-1 předmětů, a tedy hodnota A[i] je nenulová již před k-tým krokem, anebo k-tý předmět je obsažen v takové množině X.
Potom ale hodnota A[i-mk] je nenulová před k-tým krokem (hmotnost podmnožiny X bez k-tého prvku je i-mk) a hodnota A[i] se stane nenulovou v k-tém kroku.
Po provedení všech N kroků odpovídají nenulové hodnoty A[i] přesně hmotnostem podmnožin ze všech předmětů, které máme k dispozici. Speciálně největší index i0 takový, že hodnota A[i0] je nenulová, odpovídá hmotnosti nejtěžší podmnožiny předmětů, která nepřekročí hmotnost M.
Nalézt jednu množinu této hmotnosti také není obtížné: V k-tém kroku jsme měnili nulové hodnoty v poli A na hodnotu k, takže v A[i0] je uloženo číslo jednoho z předmětů nějaké takové množiny, v A[i0-mA[i0]] číslo dalšího předmětu atd. Zdrojový kód tohoto algoritmu lze nalézt níže.
Časová složitost algoritmu je O(NM), neboť se skládá z N kroků, z nichž každý vyžaduje čas O(M). Paměťová složitost činí O(N+M), což představuje paměť potřebnou pro uložení pomocného pole A a hmotností daných předmětů.
Cvičení a poznámky
- Proč pole A procházíme pozadu a ne popředu?
- Složitost algoritmu vypadá jako polynomiální, ale to je trochu podvod.
Závisí totiž na hodnotě M. Pokud tuto hodnotu na vstupu zapíšeme obvyklým
způsobem, tedy v desítkové nebo dvojkové soustavě, použijeme řádově log M cifer.
Naše M proto bude vzhledem k délce vstupu až exponenciálně velké. To je typický příklad takzvaného pseudopolynomiálního algoritmu – tedy takového, jenž je vzhledem k hodnotám na vstupu polynomiální, ale k délce vstupu exponenciální. Podrobnosti si můžete přečíst v kuchařce o těžkých úlohách.
# Již existující proměnné:
# N - počet předmětů
# M - hmotnostní omezení
# hmotnosti - pole hmotností dílčích předmětů
A = [0] * M
A[0] = 1
for k in range(N):
for i in range(M, hmotnost[k]-1, -1):
if (A[i-hmotnost[k]] != 0) and (A[i] == 0):
A[i] = k
i = M
while A[i] == 0:
i -= 1
print("Maximální hmotnost: {}" .format(i))
print("Předměty v množině:", end="")
while A[i] != -1:
print(" {}" .format(A[i]), end="")
i = i - hmotnost[A[i]]
var N: integer; { počet předmětů }
M: integer; { hmotnostní omezení }
hmotnost: array[1..N] of integer;
{ hmotnosti daných předmětů }
A: array[0..M] of integer;
i, k: integer;
begin
A[0]:=-1;
for i:=1 to M do A[i]:=0;
for k:=1 to N do
for i:=M downto hmotnost[k] do
if (A[i-hmotnost[k]]<>0) and (A[i]=0) then
A[i]:=k;
i:=M; while A[i]=0 do i:=i-1;
writeln('Maximální hmotnost: ',i);
write('Předměty v množině:');
while A[i]<>-1 do begin
write(' ',A[i]);
i:=i-hmotnost[A[i]];
end;
writeln;
end.
Nejkratší cesty a Floydův-Warshallův algoritmus
Náš další příklad bude z oblasti grafových algoritmů, ale zkusíme si jej nejdříve říci bez grafů:
Bylo-nebylo-je N měst. Mezi některými dvojicemi měst vedou (obousměrné) silnice, jejichž délky jsou dány na vstupu. Předpokládáme, že silnice se jinde než ve městech nepotkávají (pokud se kříží, tak mimoúrovňově).
Úkolem je spočítat nejkratší vzdálenosti mezi všemi dvojicemi měst, tj. délky nejkratších cest mezi všemi dvojicemi měst. Cestou rozumíme posloupnost měst takovou, že každá dvě po sobě následující města jsou spojené silnicí, a délka cesty je součet délek silnic, které tato města spojují.
V grafové terminologii tedy máme daný ohodnocený neorientovaný graf a chceme zjistit délky nejkratších cest mezi všemi dvojicemi jeho vrcholů.
Půjdeme na to následovně – vzdálenosti mezi městy jsou na začátku algoritmu uloženy ve dvourozměrném poli D, tj. D[i][j] je vzdálenost z města i do města j. Pokud mezi městy i a j nevede žádná silnice, bude D[i][j]=∞ (v programu bude tato hodnota rovna nějakému dostatečně velkému číslu).
V průběhu výpočtu si budeme na pozici D[i][j] udržovat délku nejkratší dosud nalezené cesty mezi městy i a j.
Algoritmus se skládá z N fází. Na konci k-té fáze bude v D[i][j] uložena délka nejkratší cesty mezi městy i a j, která může procházet skrz libovolná z měst 1,… ,k.
V průběhu k-té fáze tedy stačí vyzkoušet, zda je mezi městy i a j kratší stávající cesta přes města 1,… ,k-1, jejíž délka je uložena v D[i][j], nebo nová cesta přes město k.
Pokud nejkratší cesta prochází přes město k, můžeme si ji rozdělit na nejkratší cestu z i do k a nejkratší cestu z k do j. Délka takové cesty je tedy rovna D[i][k]+D[k][j].
Pokud je součet D[i][k]+D[k][j] menší než stávající hodnota D[i][j], nahradíme hodnotu na pozici D[i][j] tímto součtem, jinak ji ponecháme.
Z popisu algoritmu přímo plyne, že po N-té fázi je na pozici D[i][j] uložena délka nejkratší cesty z města i do města j.
Protože v každé z N fází algoritmu musíme vyzkoušet všechny dvojice i a j, vyžaduje každá fáze čas O(N2). Celková časová složitost našeho algoritmu tedy je O(N3). Co se paměti týče, vystačíme si s polem D a to má velikost O(N2).
Program bude vypadat následovně:
for k in range(N):
for i in range(N):
for j in range(N):
if d[i][k] + d[k][j] < d[i][j]:
d[i][j] = d[i][k] + d[k][j]
var N: integer; { počet měst }
D: array[1..N] of array[1..N] of longint;
{ délky silnic mezi městy, D[i][i]=0,
místo neexistujících je "nekonečno" }
i, j, k: integer;
begin
for k:=1 to N do
for i:=1 to N do
for j:=1 to N do
if D[i][k]+D[k][j] < D[i][j] then
D[i][j]:=D[i][k] + D[k][j];
end.

Popišme si ještě, jak bychom postupovali, kdybychom kromě vzdáleností mezi městy chtěli nalézt i nejkratší cesty mezi nimi.
To lze jednoduše vyřešit například tak, že si navíc budeme udržovat pomocné pole E[i][j] a do něj při změně hodnoty D[i][j] uložíme nejvyšší číslo města na cestě z i do j délky D[i][j] (při změně v k-té fázi je to číslo k).
Máme-li pak vypsat nejkratší cestu z i do j, vypíšeme nejprve cestu z i do E[i][j] a pak cestu z E[i][j] do j. Tyto cesty nalezneme stejným (rekurzivním) postupem.
Poznámky
- Popis algoritmu vysloveně svádí k záludné otázce: Jak víme, že spojením dvou
cest, které provádíme, vznikne zase cesta (tj. že se na ní nemohou nějaké
vrcholy opakovat)?
To samozřejmě nevíme, ale všimněme si, že kdykoliv by to cesta nebyla, tak si ji nevybereme, protože původní cesta bez vrcholu k bude vždy kratší nebo alespoň stejně dlouhá…
Tedy dokud se v naší zemi nevyskytuje cyklus záporné délky. To bychom měli přidat do předpokladů našeho algoritmu, kdybychom byli pedanti (ale hrany záporné délky stále dovolujeme, jen nesmí utvořit cyklus se záporným součtem).
- Pozor na pořadí cyklů – program vysloveně svádí k tomu, abychom psali cyklus
pro
kjako vnitřní… jenže pak samozřejmě nebude fungovat.
Cvičení
- Jak by algoritmus fungoval, kdyby silnice byly jednosměrné?
- Hodnoty v poli si přepisujeme pod rukama, takže by se nám mohly poplést hodnoty z předchozí fáze s těmi z fáze současné. Ale zachrání nás to, že čísla, o která jde, vyjdou v obou fázích stejně. Proč?
Nejdelší společná podposloupnost
Další příklad dynamického programování, který si předvedeme, se bude týkat posloupností. Mějme dvě posloupnosti čísel A a B.
Chceme najít jejich nejdelší společnou podposloupnost (NSP), tedy takovou posloupnost, kterou můžeme získat z A i B odstraněním některých prvků. Například pro posloupnosti
| A | = 2 3 3 1 2 3 2 2 3 1 1 2 |
| B | = 3 2 2 1 3 1 2 2 3 3 1 2 2 3 |
je jednou z nejdelších společných podposloupností tato posloupnost:
Jakým způsobem můžeme takovou podposloupnost najít? Nejdříve nás asi napadne vygenerovat všechny podposloupnosti a ty pak porovnat.
Jakmile si ale spočítáme, že všech podposloupností posloupnosti o délce n je 2n (každý prvek nezávisle na ostatních buď použijeme, nebo ne), najdeme raději nějaké rychlejší řešení.
Zkusme využít následující myšlenku: vyřešíme tento problém pouze pro první prvek posloupnosti A. Pak najdeme řešení pro první dva prvky A, přičemž využijeme předchozích výsledků. Takto pokračujeme pro první tři, čtyři, … až n prvků.
Nejprve si rozmyslíme, co všechno si musíme v každém kroku pamatovat, abychom z toho dokázali spočíst krok následující. Určitě nám nebude stačit pamatovat si pouze nejdelší podposloupnost, jenže množina všech společných podposloupností je už zase moc velká.
Podívejme se tedy detailněji, jak se změní tato množina při přidání dalšího prvku k A: Všechny podposloupnosti, které v množině byly, tam zůstanou a navíc přibyde několik nových, končících právě přidaným prvkem.
Ovšem my si podposloupnosti pamatujeme proto, abychom je časem rozšířili na nejdelší společnou podposloupnost.
Takže pokud známe nějaké dvě stejně dlouhé podposloupnosti P a Q končící nově přidaným prvkem v A a víme, že P končí v B dříve než Q, stačí si z nich pamatovat pouze P.
V libovolném rozšíření Q-čka totiž můžeme Q vyměnit za P a získat tím stejně dlouhou společnou podposloupnost.
Proto si stačí pro již zpracovaných a prvků posloupnosti A pamatovat pro každou délku l tu ze společných podposloupností A[1… a] a B délky l, která v B končí na nejlevějším možném místě. Dokonce nám bude stačit si místo celé podposloupnosti uložit jen pozici jejího konce v B. K tomu použijeme dvojrozměrné pole D[a,l].
Ještě si dovolíme jedno malé pozorování: Koncové pozice uložené v poli D se zvětšují s rostoucí délkou podposloupnosti, čili D[a,l]<D[a,l+1], protože posloupnosti délky l+1 nejsou ničím jiným než rozšířeními posloupností délky l o 1 prvek.
Teď již výpočet samotný. Pokud už známe celý a-tý řádek pole D, můžeme z něj získat (a+1)-ní řádek. Projdeme postupně posloupnost B. Když najdeme v B prvek A[a+1] (ten právě přidávaný do A), můžeme rozšířit všechny podposloupnosti končící před aktuální pozicí v B.
Nás bude zajímat pouze ta nejdelší z nich, protože rozšířením všech kratších získáme posloupnost, jejíž koncová pozice je větší než koncová pozice některé posloupnosti, kterou již známe. Rozšíříme tedy tu nejdelší podposloupnost a uložíme ji místo původní podposloupnosti.
Toto provedeme pro každý výskyt nového prvku v posloupnosti B. Všimněme si, že nemusíme procházet pole s podposloupnostmi stále od začátku, ale můžeme se v něm posouvat od nejmenší délky k největší.
Ukážeme si, jak vypadá zaplněné pole hodnotami při řešení problému z našeho příkladu. Abychom nemuseli listovat, tak si zde zadání příkladu uvedeme ještě jednou – hledáme NSP těchto dvou posloupností:
| A | = 2 3 3 1 2 3 2 2 3 1 1 2 |
| B | = 3 2 2 1 3 1 2 2 3 3 1 2 2 3 |
Nyní už slíbená tabulka znázorňující výpočet. Řádky jsou pozice v A, sloupce délky podposloupností.
| D | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 2 | - | - | - | - | - | - | - | - | - | - | - |
| 2 | 1 | 5 | - | - | - | - | - | - | - | - | - | - |
| 3 | 1 | 5 | 9 | - | - | - | - | - | - | - | - | - |
| 4 | 1 | 4 | 6 | 11 | - | - | - | - | - | - | - | - |
| 5 | 1 | 2 | 5 | 7 | 12 | - | - | - | - | - | - | - |
| 6 | 1 | 2 | 3 | 7 | 9 | 14 | - | - | - | - | - | - |
| 7 | 1 | 2 | 3 | 7 | 8 | 12 | - | - | - | - | - | - |
| 8 | 1 | 2 | 3 | 7 | 8 | 12 | 13 | - | - | - | - | - |
| 9 | 1 | 2 | 3 | 5 | 8 | 9 | 13 | 14 | - | - | - | - |
| 10 | 1 | 2 | 3 | 4 | 6 | 9 | 11 | 14 | - | - | - | - |
| 11 | 1 | 2 | 3 | 4 | 6 | 9 | 11 | 14 | - | - | - | - |
| 12 | 1 | 2 | 3 | 4 | 6 | 7 | 11 | 12 | - | - | - | - |
Zbývá popsat, jak z těchto dat zvládneme rekonstruovat hledanou nejdelší společnou podposloupnost (NSP).
Ukážeme si to na našem příkladu – jelikož poslední nenulové číslo na posledním řádku je v 8. sloupci, má hledaná NSP délku 8.
D[12, 8]=12 říká, že poslední písmeno NSP je na pozici 12 v posloupnosti B. Jeho pozici v posloupnosti A určuje nejvyšší řádek, ve kterém se tato hodnota také vyskytuje, v našem případě je to řádek 12. Druhé písmeno tedy budeme určovat z D[10, 7], třetí z D[9, 6], atd.
Jednou z hledaných podposloupností je tedy:
| poslupnost: | 2 | 3 | 1 | 2 | 2 | 3 | 1 | 2 |
| indexy v A: | 1 | 2 | 4 | 5 | 7 | 9 | 10 | 12 |
| indexy v B: | 2 | 5 | 6 | 7 | 8 | 9 | 11 | 12 |
Již zbývá jen odhadnout složitost algoritmu. Časově nejnáročnější byl vlastní výpočet hodnot v poli, který se skládá ze dvou hlavních cyklů o délce |A| a |B|, což jsou délky posloupností A a B.
Vnořený cyklus while proběhne celkem maximálně |A|-krát a časovou složitost nám nezhorší. Můžeme tedy říct, že časová složitost je O(|A| · |B|).
Posloupnosti jsme si prohodili tak, aby první byla ta kratší, protože pak jsou maximální délka společné podposloupnosti i počet kroků algoritmu rovny délce kratší posloupnosti, a tedy i velikost pole s daty je kvadrát této délky.
Paměťovou složitost odhadneme O(N2+M), kde N je délka kratší posloupnosti a M té delší.
# Načtení posloupností s dovolením vynecháme
if lenA > lenB: # v A bude kratší
(A, B) = (B, A)
(lenA, lenB) = (lenB, lenA)
d = [[lenB] * lenA for i in range(lenA)]
maxLen = 0
for i in range(lenA):
l = 0
# Máme minimálně to samé, co minule
if i > 0:
for j in range(lenA):
d[i][j] = d[i - 1][j]
for j in range(lenB):
if B[j] == A[i]:
while i > 0 and d[i - 1][l] < j:
l += 1
if d[i][l] >= j:
d[i][l] = j
maxLen = max(l + 1, maxLen)
j = lenA - 1
C = [None] * maxLen
for i in range(maxLen):
ii = maxLen - i - 1
while j > 0 and d[j][ii] == d[j - 1][ii]:
j -= 1
C[ii] = A[j]
j -= 1
# Nyní je v C spočtená NSP posloupností A a B
program Podposloupnost;
var
A, B, C: array[0..MaxN - 1] of Integer;
lenA, lenB: Integer; { Délky posloupností }
D: array[0..MaxN, 1..MaxN] of Integer;
I, J, L, MaxLen: Integer;
begin
{ Načtení posloupností s dovolením vynecháme }
if lenA > lenB then begin { A bude kratší z obou }
C := A;
A := B;
B := C;
L := lenA;
lenA := lenB;
lenB := L;
end;
for I := 1 to lenA do
D[0, I] := lenB;
L := 0;
MaxLen := 0;
for I := 1 to lenA do begin
for J := 1 to lenA do
D[I, J] := D[I-1, J];
L := 0;
for J := 0 to lenB-1 do
if B[J] = A[I-1] then begin
while (L = 0) or (D[I-1, L] < J) do
L:=L+1;
if D[I, L] >= J then
D[I, L] := J;
end;
if L > MaxLen then MaxLen := L;
end;
J := lenA;
for I := MaxLen downto 1 do
begin
while D[J-1, I] = D[J, I] do J:=J-1;
C[I-1] := A[J-1];
J:=J-1;
end;
{ Nyní je v C spočtená NSP posloupností A a B }
end.
Nejdelší rostoucí podposloupnost
Když už jsme u posloupností, povězme si ještě o jedné známé úloze: hledání nejdelší rostoucí podposloupnosti (NRP). Tentokrát máme posloupnost jen jednu a naším cílem je vybrat z ní co nejdelší rostoucí podposloupnost, tedy vyškrtat co nejméně prvků tak, aby zbylá posloupnost byla rostoucí.
Když si tipneme, že problém hledání NRP jde vyřešit dynamickým programováním, nabízí se otázka, jak ho rozdělit na menší problémy, stejně jako jsme to udělali u předchozích problémů. Můžeme třeba spočítat nejdříve NRP pro první prvek, pak pro první dva prvky, …, až spočteme NRP celého P, přičemž se vždy k dosavadnímu NRP v každém kroku pokoušíme přidat aktuální prvek. To je úvaha správným směrem, ale sama o sobě nefunguje: důkazem budiž P = [4, 5, 1, 2, 3], kde nesprávně odpovíme [4, 5]. Potíž je v tom, že si toho počítáme příliš málo a neumíme pak z odpovědí pro menší problémy počítat odpovědi pro problémy větší. Hladově se pak zafixujeme na nějakou podposloupnost, která se ze začátku jeví optimální, ale nakonec není.
Pojďme to napravit. Místo, abychom si udržovali jen průběžnou NRP, budeme si rostoucích podposloupností (RP) udržovat více. Konkrétně si pro každé k budeme udržovat, jestli z dosavadních prvků umíme vyrobit RP délky k, a pokud ano, tak na jakou nejnižší hodnotou taková RP může končit. Formálně tuto hodnotu označíme A[i][k], kde i je počet zatím zpracovaných prvků P a k kýžená délka RP. Snadno nahlédneme, že finální délku NRP na konci získáme z A[N] tak, že se podíváme, pro jaké největší k ještě A[N][k] existuje.
Zbývá popsat, jak pomocí A[i - 1] a aktuálního prvku P[i] spočítat A[i][k]. K tomu stačí rozlišit dvě možnosti, jak taková RP může vypadat, a vzít z nich tu lepší: Buď nejlepší RP reprezentovaná v A[i][k] má končit na P[i], nebo nikoliv. Pokud RP na P[i] nemá končit, pak nutně A[i][k] = A[i - 1][k], jelikož nově přidaný prvek v RP nijak nevyužíváme. Pokud naopak RP na P[i] končit má, pak A[i][k] = P[i]. Tuto možnost ale smíme použít pouze v případě, že nějaká taková RP vskutku existuje – to jest, pokud můžeme vzít nějakou podposloupnost délky k - 1 a za ni P[i] nalepit. To ověříme snadno – prostě P[i] porovnáme s A[i - 1][k - 1], a pokud je P[i] menší, znamená to, že ani za co nejníže končící RP délky k - 1 ho nalepit nejde, a tudíž ho použít nesmíme.
Aby měl náš algoritmus kde začít, inicializujeme A[0][0] na minus nekonečno. Tuto prázdnou posloupnost půjde rozšířit každým prvkem z P.
Pro důkaz správnosti stačí nahlédnout, že jsou-li hodnoty A[i - 1] spočítány správně, pak i každé A[i][k] bude správně. Spokojíme se s neformálními úvahami z předchozího odstavce, pro formální důkaz bychom měli důkladněji ověřit, že každá potenciálně lepší RP bude pokrytá jednou ze dvou rozebíraných možností.
Časová složitost tohoto řešení je O(NK), kde K ≤ N je délka NRP. Paměťová složitost je též O(NK), ale můžeme ji zlepšit na O(K), budeme-li si místo celého A pamatovat vždy jen dva poslední řádky.
K rychlejšímu řešení nás dovede pozorování: Umíme něco říct o vzájemném vztahu A[i][0], A[i][1], … , A[i][k]? Jinými slovy, když z nějakého pole vybíráme stále delší a delší RP, co můžeme říct o nejnižších dosažitelných hodnotách posledních prvků? Nahlédneme, že musejí růst: Máme-li RP odpovídající A[i][k], můžeme z ní odebrat poslední prvek x, čímž dostaneme nějakou RP délky k - 1, s posledním prvkem y < x. Teď sice nevíme, jaká optimální RP je v A[i][k - 1], ale jelikož to je optimální RP délky k - 1 a my jsme právě vyrobili nějakou RP délky k - 1, musí nutně platit, že A[i][k - 1] ≤ y < x = A[i][k].
Učiníme ještě druhé pozorování: A[i] se od A[i - 1] liší nejvýše jedním prvkem. Každý odlišný prvek v A[i] totiž musí mít hodnotu rovnou P[i], a ta se v ostře rostoucí posloupnosti A[i] může objevit nejvýše jednou.
Konkrétně, pokud jsme změnili prvek A[i][k], pak určitě P[i] < A[i - 1][k] (jinak bychom v posloupnosti nechali A[i - 1][k], protože je lepší) a zároveň P[i] > A[i - 1][k - 1] (jinak P[i] nesmíme použít). To nám ale dává návod na rychlý algoritmus: místo, abychom A[i] vždy v O(N) počítali z A[i - 1], stačí nejprve binárním vyhledáváním najít správné k, A[i - 1][k] upravit, a pak A[i - 1] prostě prohlásit za A[i]. Nemusíme si tedy vůbec počítat dvojrozměrnou tabulku, ale bude nám stačit obyčejné pole, které pod rukama měníme.
Časová složitost takového řešení je O(N log N), paměťová O(N). Na závěr si ještě rozmysleme, jak kromě délky NRP i tuto podposloupnost vypsat. K tomu si stačí v každém kroku poznačit, jakou hodnotu jsme právě upravili. Po spočtení NRP pak tento záznam úprav můžeme pozpátku projít a vypsat ta i, ve kterých jsme naši budoucí NRP prodlužovali. Pro detaily nahlédněte do vzorového řešení.
# Modul na binární vyhledávání ze standardní knihovny:
import bisect
# Načteme vstup. Od pozic odečteme jedničku, protože je chceme číslovat od nuly.
P = [int(x) - 1 for x in input().split()]
# V `nejnizsi[k]` si udržujeme, na jakou nejnižší hodnotu může končit rostoucí podposloupnost délky
# `k` (pro zatím prošlou část pole). Hodnota `nejnizsi[k]` odpovídá hodnotě `A[i][k]` z textu.
nejnizsi = []
# V `zaznam[i]` si ukládáme, jakou hodnotu pole `nejnizsi` jsme upravili v i-tém kroku.
zaznam = []
for x in P:
# Najdeme i takové, že nejnizsi[i - 1] < x <= nejnizsi[i]
i = bisect.bisect_left(nejnizsi, x)
if i == len(nejnizsi):
# Prodlužujeme dosud nejdelší rostoucí posloupnost, potřebujeme přidat dummy prvek.
nejnizsi.append(None)
nejnizsi[i] = x
zaznam.append(i)
# Hledáme největší `k`, pro které je `nejnizsi[k]` spočítané, což je přesně `len(nejnizsi) - 1`,
# plus `1` za indexování od jedničky.
print(len(nejnizsi))
# Teď projdeme záznam pozpátku a sledujeme pozici posloupnosti, ze které se na konci stane NRP. Na
# začátku je na poslední pozici v poli a pokaždé, když z aktuálního záznamu vyplývá, že jsme v
# aktuálním kroku NRP prodloužili, snížíme `nrp` o jedna.
nrp = len(nejnizsi) - 1
res = []
# enumerate(seznam) vrací iterátor (0, seznam[0]), (1, seznam[1]), …
for i, a in reversed(list(enumerate(zaznam))):
# Pokud aktuální akce prodloužila podposloupnost, ze které se na konci stane NRP:
if a == nrp:
# + 1 kvůli číslování od nuly
res.append(i + 1)
nrp -= 1
print(" ".join(map(str, reversed(res))))