Recepty z programátorské kuchařky
Toky v sítích
Aktuální verze kuchařky: prosinec 2019
Ukážeme si uměle znějící úlohu, kterou posléze zmatematizujeme, vyřešíme a dokážeme vlastnosti řešení. Nakonec přijdou četná užití, která ozřejmí, proč jsme se snažili.
Látka je lehce pokročilá, takže vězte, že budete potřebovat znát grafy.
Uměle znějící úloha
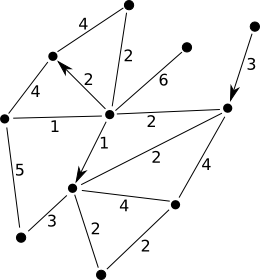
Ruský petrobaron vlastní ropná naleziště na Sibiři a trubky vedoucí do Evropy. Trubky vedou mezi nalezišti, uzlovými body a koncovými body, kde ropu přebírají odběratelé.
Každá trubka může a nemusí mít definováno, kterým směrem jí má téci ropa. Pro každou trubku zvlášť víme, kolik nejvýše jí za hodinu protlačíme.
Naleziště jsou bezedná a mohou posílat neomezená množství ropy. Odběratelé také dokáží neomezená množství ropy z koncových bodů odebírat. Petrobaron čelí problému, jak protlačit danou distribuční sítí co nejvíce ropy za hodinu ze zdrojů k odběratelům.
Zapeklité je to zejména kvůli tomu, že v uzlových bodech nelze ropu hromadit, ani pálit – rozhodně tedy nejde bez rozmyslu přikázat, ať každou trubkou teče maximum, protože bychom poškodili cenná zařízení a v uniklé ropě utopili vše živé.
Zmatematizování
V zadání vidíme graf, který obsahuje orientované i neorientované hrany, kde je nějaká podmnožina vrcholů označená jako zdroje a jiná jako… říkejme tomu třeba stoky.
Abychom měli situaci jednodušší, zbavíme se hned na úvod mnohočetnosti zdrojů a stoků. Přikreslíme si dva nové vrcholy – z nadzdroje budeme posílat ropu do všech zdrojů, do nadstoku budeme posílat ropu ze všech stoků. Kapacitu přikreslených hran pak nastavíme na nekonečno.
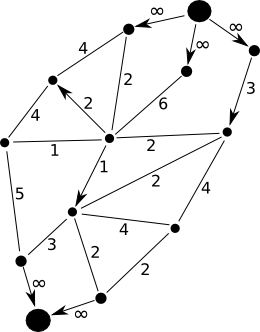
Teď nám stačí vymyslet algoritmus, který řeší problém s právě jedním zdrojem a právě jedním stokem.
Každý vstup totiž popsaným způsobem převedeme, pošleme ho algoritmu a z výstupu prostě jen odstraníme dva přidané vrcholy a připojené hrany.
Podobně se zbavíme neorientovaných hran.
Každou takovou hranu v každém zadání změníme na dvojici protisměrných orientovaných hran se stejnou kapacitou. V algoritmu pak už můžeme počítat jen s hranami orientovanými.
Dostáváme se nyní k nejdůležitějšímu – podmínkám na hledaný tok.
Na vstupu dostáváme ohodnocení hran nezápornými čísly a naším úkolem je sestavit jiné ohodnocení těch samých (všech) hran.
Je důležité, aby se nám to nepletlo – ohodnocení ze vstupu se říká kapacita a značí se c(e), konstruované ohodnocení se jmenuje tok a označujeme ho f(e).
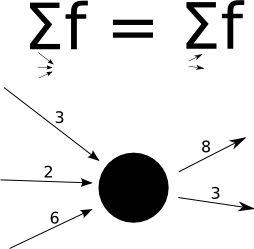
Konstruované ohodnocení se snažíme maximalizovat, ale omezuje nás kapacita a Kirchhoffův zákon.
Tak budeme říkat podmínce na to, že součet toku na hranách, které do vrcholu vstupují, musí být stejný jako součet toku na hranách, které z vrcholu vystupují. Máte-li rádi fyziku nebo berete-li školu vážně, důvod k takovému pojmenování jistě chápete.
Formálně ony dvě podmínky vypadají takto:
Kirchhoffova podmínka se samozřejmě netýká ani zdroje, ani stoku – tam nám naopak jde o to ji co nejvíce porušit. Velikost toku je nejsnazší měřit na nich. Budeme ji definovat jako rozdíl mezi součtem odtoků a součtem přítoků ve zdroji.
K zamyšlení
- Nastavit ohodnocení hrany (kapacitu) na skutečné nekonečno v našem programovacím jazyce nemusí jít. Pak se to řeší tím, že se zvolí dostatečně velké číslo. Jak co nejmenší, ale stále bezpečné, rychle ze zadání určit? Stejný problém se řeší třeba v Dijkstrově algoritmu, ale i ve spoustě dalších.
- Neorientované hrany, neboli obousměrné trubky, si zaslouží podrobnější rozbor, než jaký jsme jim věnovali v textu. Jak spolehlivě převedeme řešení algoritmu do původní sítě?
- Vymysleli jsme, jak vyřešit více zdrojů a stoků a jak ošetřit obousměrné trubky. Co kdyby bylo v zadání omezení na průtok vrcholy?
- Umíte dokázat, že je absolutní hodnota rozdílu přítoků a odtoků stejná na zdroji i na stoku? Tedy že bychom mohli velikost toku stejně tak dobře měřit i na stoku?
Řešení
Problém je velmi studovaný a k jeho řešení existují dva velké přístupy, které jsou humorně protikladné. Ten první vezme nulový tok a opatrně ho zlepšuje. Druhý si napíská veliké ohodnocení hran, které ani tokem není, a pak ho opravuje.
Předvedeme si onen první způsob a algoritmus, který se podle svých autorů jmenuje Fordův-Fulkersonův. Bude se nám odteď hodit tvářit se, jako že mezi každými dvěma vrcholy vede oběma směry hrana. Tam, kde ze vstupu nepřišla, si domyslíme jednu s nulovou kapacitou.
Představme si graf, na kterém počítáme tok, a dejme tomu, že už nějaký tok máme – třeba prázdný. Představme si, že jsme ropný magnát a každý rozdíl mezi kapacitou potrubí a jejím využitím (tokem) nás stojí miliony dolarů.
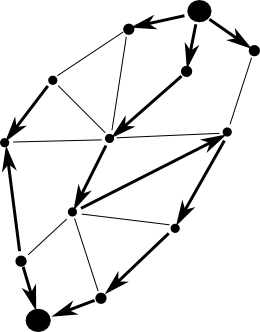
Už jsme se smířili s tím, že každá trubka nemůže být využita na maximum, ale zkusme si vyznačit ty hrany, kde c(e)≠ f(e).
Co když existuje cesta z nadzdroje do nadstoku, která vede pouze po takových hranách?
Můžeme vzít minimum z rozdílů na každé hraně a o toto číslo navýšit tok na každé z nich! Ani kapacitní, ani Kirchhoffovu podmínku to jistě nepoškodí.
Pokud žádnou takovou cestu nevidíme, znamená to, že tok vylepšit nejde? Ne úplně. Představte si následující situaci:

Copak nejde zlepšit? Jde! Není na to první pohled úplně jasné, ale můžeme zlepšovat výsledný tok i tím, že ho na protisměrné části cesty snížíme. Samozřejmě však nesmíme nastavovat tok záporný.
(Je smutné, že si teď trochu kazíme grafovou terminologii – co je to za cestu v orientovaném grafu, která nemusí respektovat orientaci hran?)
Takže jaká je přesně podmínka pro „vyznačení“ hrany uv→? Nastává f(uv→) < c(uv→) nebo f(vu→) > 0. Potom ji lze zlepšit o c(uv→)-f(uv→)+f(vu→).
Hledání všech vhodných („zlepšujících“) cest tedy můžeme dělat prostým prohledáváním do šířky přes vyznačené hrany. Budeme to dělat opakovaně znovu a znovu, až žádnou takovou nenajdeme, a pak vrátíme získaný tok jako výsledek.
Analýza algoritmu
Správnost
Zavolali jsme algoritmus na prázdný tok, ten ho zlepšil do situace, ve které neexistuje zlepšující cesta.
Znamená tato neexistence, že je výsledný tok maximální? Opačná implikace je jasná – maximální tok zlepšit žádným způsobem nepůjde, takže ani přes zlepšující cestičky.
Když zkusíme algoritmus pustit na graf, kde už žádná taková cesta není, můžeme si poznamenat všechny vrcholy, kam jsme se pomocí prohledávání zlepšitelných hran ještě dostali. Tato množina bude jistě obsahovat zdroj (tam jsme začali) a jistě nebude obsahovat stok (to by existovala zlepšující cesta).
Na hranách mezi touto množinou a jejím doplňkem nemůžeme zlepšovat, jinak by se po nich náš program pustil dál a množinu vrcholů, kam se dostal, by rozšířil. Všechny hrany směřující ven tedy mají f(e)=c(e), pro všechny hrany směřující dovnitř platí f(e)=0.
Tyto hrany tvoří řez naším grafem. Odvoláme se v tuto chvíli na vaši intuici – tok nemůže být větší než libovolný řez. Z toho už dostáváme, že náš algoritmus našel tok maximální, protože našel také řez, který zaručuje, že nemůže existovat tok větší.
Formálnější předvedení najdete ve skriptíčkách z kombinatoriky.
Časová složitost
Je možné dobu běhu omezit počtem vrcholů a hran? Výše uvedeným postupem na grafu s celočíselnými kapacitami každou nalezenou cestou zvýšíme tok alespoň o jednotku, takže program nebude běžet déle, než je součet všech kapacit. Ale to není moc uspokojivý odhad, protože záleží na ohodnocení.
Pokud budeme hledat cesty skutečně prohledáváním do šířky, bude počet kroků v O(nm2), protože se dá ukázat, že se hrany, které při zlepšování cesty tvoří minimum, postupně vzdalují od zdroje. Pak máme O(m) času k nalezení cesty a m hran, které se nejvýše n-krát mohou vzdálit. Že to tak skutečně je, je lehce zdlouhavé intelektuální cvičení. Nechat si prozradit postup můžete třeba v druhém vydání Introduction to Algorithms na straně 662.
O vylepšení daného postupu si můžete přečíst v kapitole o tocích v knize Průvodce labyrintem algoritmů od Martina Mareše, ukázka druhého přístupu k řešení hledání maximálního toku je tam také.
K zamyšlení
- Důležitou vlastností algoritmu je, že když dostane celočíselné kapacity, vrátí celočíselný tok. Bude se nám to hodit v aplikacích. Dokážete to?
- Rozdíl mezi Fordem-Fulkersonem, který hledá cesty obecným způsobem, a takovým, který to dělá prohledáváním do šířky, je ze složitostního hlediska docela velký, a proto se tomu druhému občas říká Edmondsův-Karpův. Najděte malý graf a nevhodnou posloupnost cest, která způsobí, že F-F poběží skutečně v závislosti na velikosti kapacit.
- Můžete dokonce zkusit využít zlatého řezu k nalezení grafu s reálnými kapacitami, na kterém F-F pro danou (nešikovnou) posloupnost cest nikdy neskončí.
- Skončí algoritmus v konečném čase, jsou-li kapacity čísla racionální?
Užití
Párování v bipartitních grafech
Máme-li za úkol najít na plese co nejvíce tanečnicím tanečníka, kterého znají, stojíme před zásadním a nelehkým úkolem.
Co třeba postavit na základě známosti bipartitní graf mezi partitou tanečníků a partitou tanečnic, přidat zdroj za kluky a stok za holky, tyto k nim připojit hranami s jednotkovou kapacitou, hranám v bipartitním grafu také nastavit jednotkové kapacity a nakonec všechno zorientovat směrem do stoku?
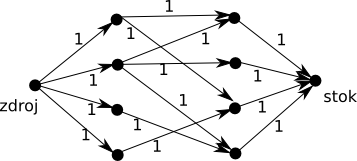
Maximální celočíselný tok, který na tomto grafu získáme, nám hrany bipartitního grafu rozdělí na nevybrané s tokem 0 a vybrané s tokem 1. Můžou vybrané hrany sdílet tanečníka? Těžko, když do něj teče nejvýše jednotkový tok a musí platit Kirchhoffův zákon. A podobně s tanečnicemi.
Vybrané hrany nám proto vytvoří párování. A protože jsme našli maximální tok, jde o párování největší. Kdyby existovalo párování větší, dokázali bychom z něj zvětšit tok.
Hledání hranově a vrcholově disjunktních cest
Chceme-li se v grafu G dostat z vrcholu u do vrcholu v, může nás zajímat (třeba kvůli spolehlivosti, s jakou se umíme dostat do cíle), kolik mezi nimi existuje cest, které:
- nesdílí hrany, nebo
- nesdílí vrcholy. (Tato podmínka je silnější. Když dvě cesty nesdílí vrcholy, nesdílí hrany.)
Oba tyto problémy lze převést na hledání maximálního toku. V obou případech nastavíme u jako zdroj a v jako stok. V prvním případě nastavíme jednotkové kapacity všem hranám, v druhém navíc všem vrcholům.
Ford-Fulkerson nastavil některým hranám jednotkový tok, některým nulový. Nulové nyní z grafu vyhodíme. Pokud jsme hledali hranově disjunktní cesty, můžeme nyní získat třeba takovýto graf:
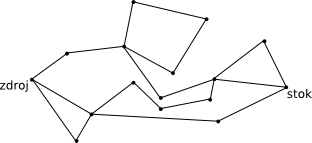
Jak z něj vykřesat kýžený výsledek? Začneme procházet ze zdroje zbylé hrany. Vždy, když se dostaneme do vrcholu, ve kterém už jsme v tom samém průchodu byli, vyhodíme z grafu všechny hrany cyklu, který jsme tímto objevili. (Hodnota toku se tím nezmění.)
Průchodem grafu se vždy můžeme dostat až do stoku (všude jinde budeme moci podle Kirchhoffova zákona jít dál – dost to připomíná úvahu o eulerovských tazích), a protože jsme mezitím agilně odstraňovali cykly, dostali jsme cestu. Vrátíme ji jako jeden výsledek, smažeme její hrany, a pokud ještě tok není nulový, pokračujeme dál.
Počet cest je tedy velikost toku. Podle Mengerovy věty je navíc počet hranově/vrcholově disjunktních cest roven stupni hranové/vrcholové souvislosti grafu – máme tedy nyní algoritmus, který ji najde.
K zamyšlení
- Úvaha nebyla naprosto přímočará kvůli cyklům v nalezeném toku. Říká se jim cirkulace. Je jasné, že v případě hledání hranově disjunktních cest vzniknout mohou. Co v případě vrcholově disjunktních, tedy v situaci, kdy jsme omezili tok vrcholy?
- Nepracuje náhodou neupravený Edmondsův-Karpův algoritmus rychleji, pokud je graf, jak jsme teď opakovaně viděli, ohodnocený toliko nulami a jedničkami?